基于響應面法的圓筒型永磁直線電機推力特性優化

付 豪，吳堯輝

(河南理工大學 電氣工程及其自動化學院，焦作 45400)

0 引 言

圓筒型永磁直線電機(以下簡稱TPMLM)具有推力密度大、動態響應快、運行可靠、無橫向邊端效應等優點[1-3]，在油田抽油機[4]、精密機床等[5]高動態響應伺服場合以及直線驅動領域得到了廣泛的應用。

然而，TPMLM定子鐵心兩端開斷和定子開槽，其存在端部效應[6]和齒槽效應[7]。由齒槽效應引起的齒槽力和端部效應引起的端部力，導致TPMLM存在較大的推力波動，嚴重影響了電機運行性能，也限制了其應用范圍。因此，減小電機的推力波動，提高平均推力，以獲得良好的推力特性至關重要。

針對此問題，國內外學者在電機本體結構上做了大量的研究。文獻[8]提出了一種初級斜端部結構，有限元仿真結果表明，其可以有效減小TPMLM的端部力，從而降低推力波動；文獻[9]通過采用不等寬槽口，來減小TPMLM的齒槽力，樣機實驗證明該方法可以有效地降低推力波動；文獻[10]通過在初級齒部加附加槽來減小TPMLM的推力波動，并對附加槽的形狀和最佳尺寸進行了研究；文獻[11]提出一種采用定子和動子不等極距的方法來減小TPMLM的齒槽力；文獻[12]采用輔助槽來減小TPMLM的齒槽力，并研究了輔助槽尺寸對TPMLM齒槽力的影響；文獻[13]提出優化電機的極弧系數來減小永磁直線電機的齒槽力；文獻[14]提出一種磁極分組偏移的方法來減小電機齒槽力。永磁電機各參數之間的耦合性是極強的，雖然這些方法可以有效地降低推力波動，但也可能降低電機的推力，影響電機的推力特性。

本文基于有限元分析，以TPMLM的平均推力和推力波動為優化目標，優化電機結構參數設計。首先，采用田口法分析電機結構參數的敏感性，從8個結構參數中選出4個敏感參數；然后，構建基于Box-Behnken法的響應面模型，采用NSGA-II多目標遺傳優化算法對該響應面模型進行求解；最后進行了有限元仿真驗證。

1 電機結構及參數

本文以9槽10極TPMLM為研究對象，圖1為圓柱坐標系下電機的模型，圖2給出了TPMLM的8個結構參數，包括定子齒部高度h0和h1，定子齒部寬度w2,槽部高度h2,槽部寬度w3，氣隙寬度w4，磁極寬度w1，磁極高度h3。TPMLM的結構參數如表1所示。

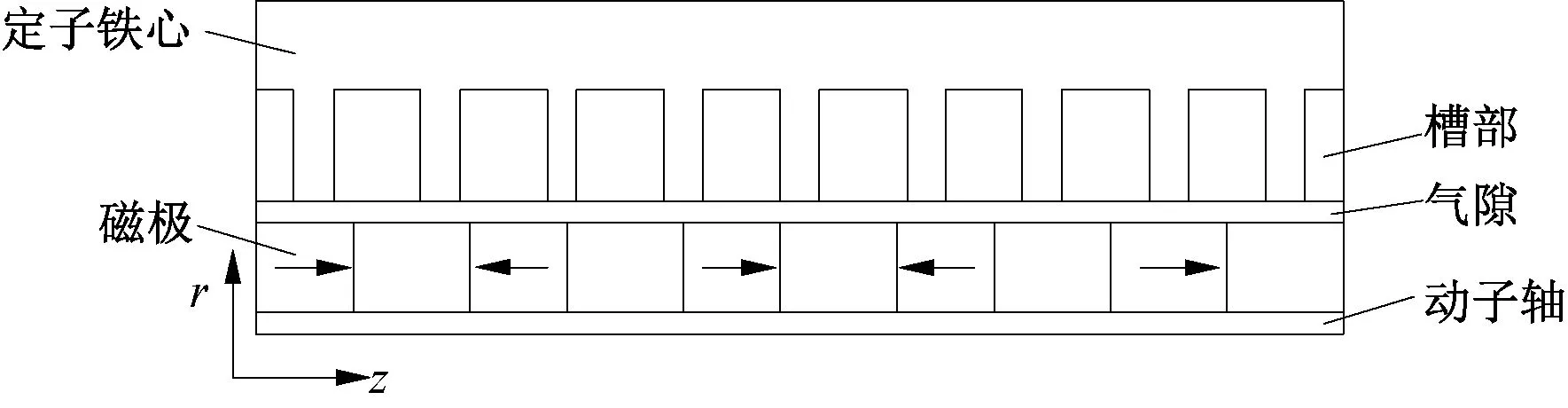
圖1 TPMLM模型

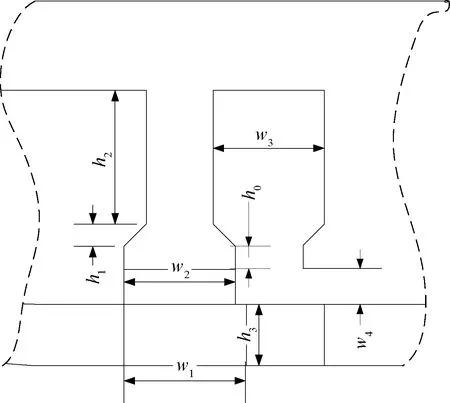
圖2 TPMLM結構參數

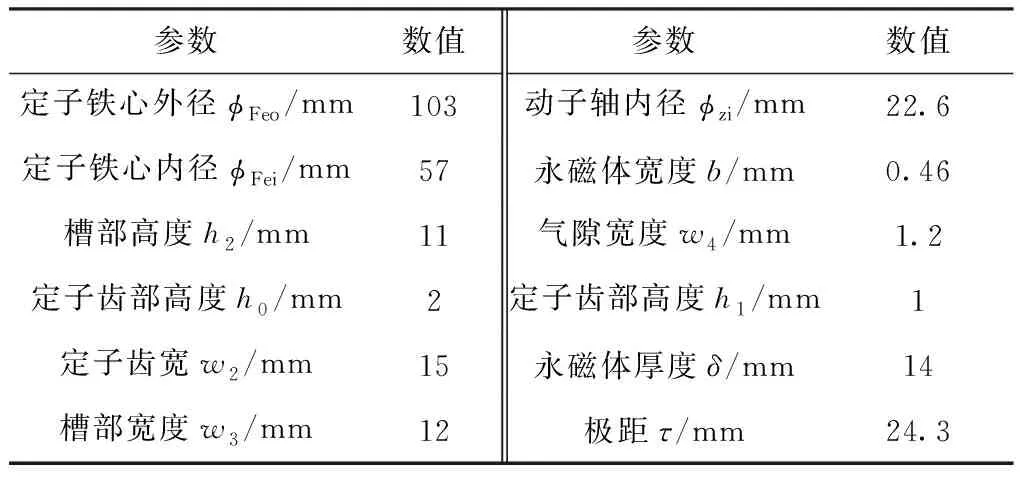
表1 TPMLM結構參數

2 參數敏感性分析

為了降低優化問題維度，提高優化效率，從這8個結構參數中選出對TPMLM推力和推力波動有顯著影響的參數。首先，將8個結構參數分為兩組：第一組是關于定子齒部的結構參數h0，h1，w2；第二組是其它的5個結構參數h2，h3，w1，w3，w4。然后，采用田口法，分別對這兩組參數建立正交實驗矩陣，通過方差分析和信噪比分析，選出對TPMLM推力和推力波動有顯著影響的參數。

2.1 第一組結構參數敏感性分析

首先，對定子齒部的3個結構參數進行實驗設計，如表2所示。接著，利用有限元軟件Magnet計算出每次實驗的目標值，填入表2中，對表2進行方差分析和信噪比分析。圖3為推力波動的信噪比，圖4為平均推力的信噪比，方差分析結果如表3所示。

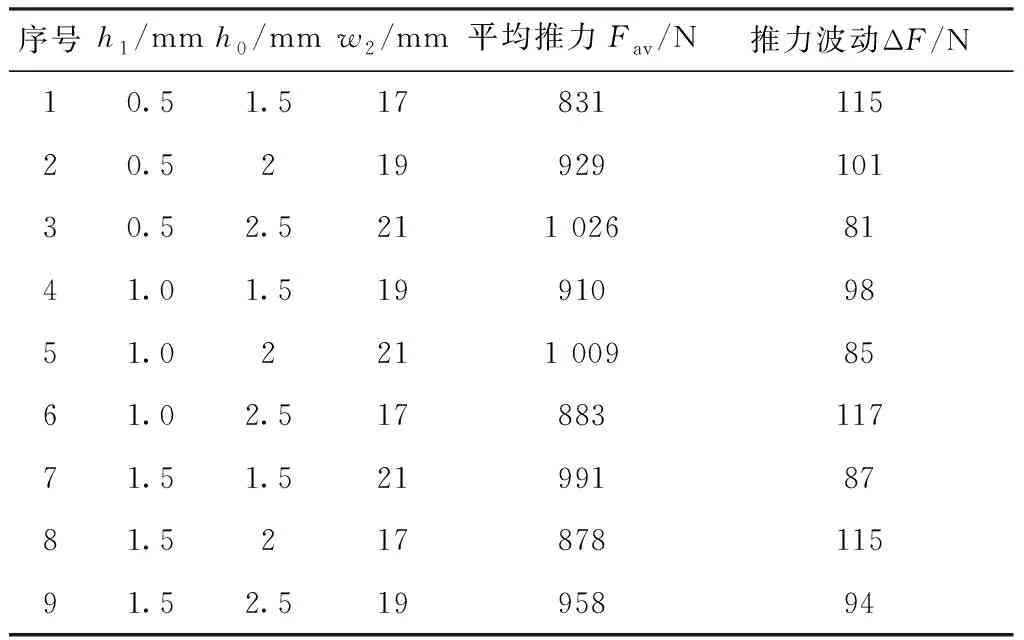
表2 第一組結構參數正交表及分析結果

圖3 第一組參數推力波動的信噪比

圖4 第一組參數平均推力的信噪比

表3 第一組參數方差分析

由圖3、圖4和表3可看出，定子齒部結構參數w2對推力波動和平均推力都有顯著影響，而h0和h1對推力波動和平均推力影響比重都小，因此將w2確定為優化變量。根據圖3和圖4的信噪比分析結果，取h0=2.5 mm,h1=1.5 mm。

2.2 第二組結構參數敏感性分析

同樣，建立一張關于h2，h3，w1，w3，w45個結構參數的L1645正交表，表4為這5個參數的正交表和有限元分析結果，圖5和圖6分別為第二組參數推力波動和平均推力的信噪比分析結果，表5為方差分析結果。

表4 第二組結構參數正交表及分析結果

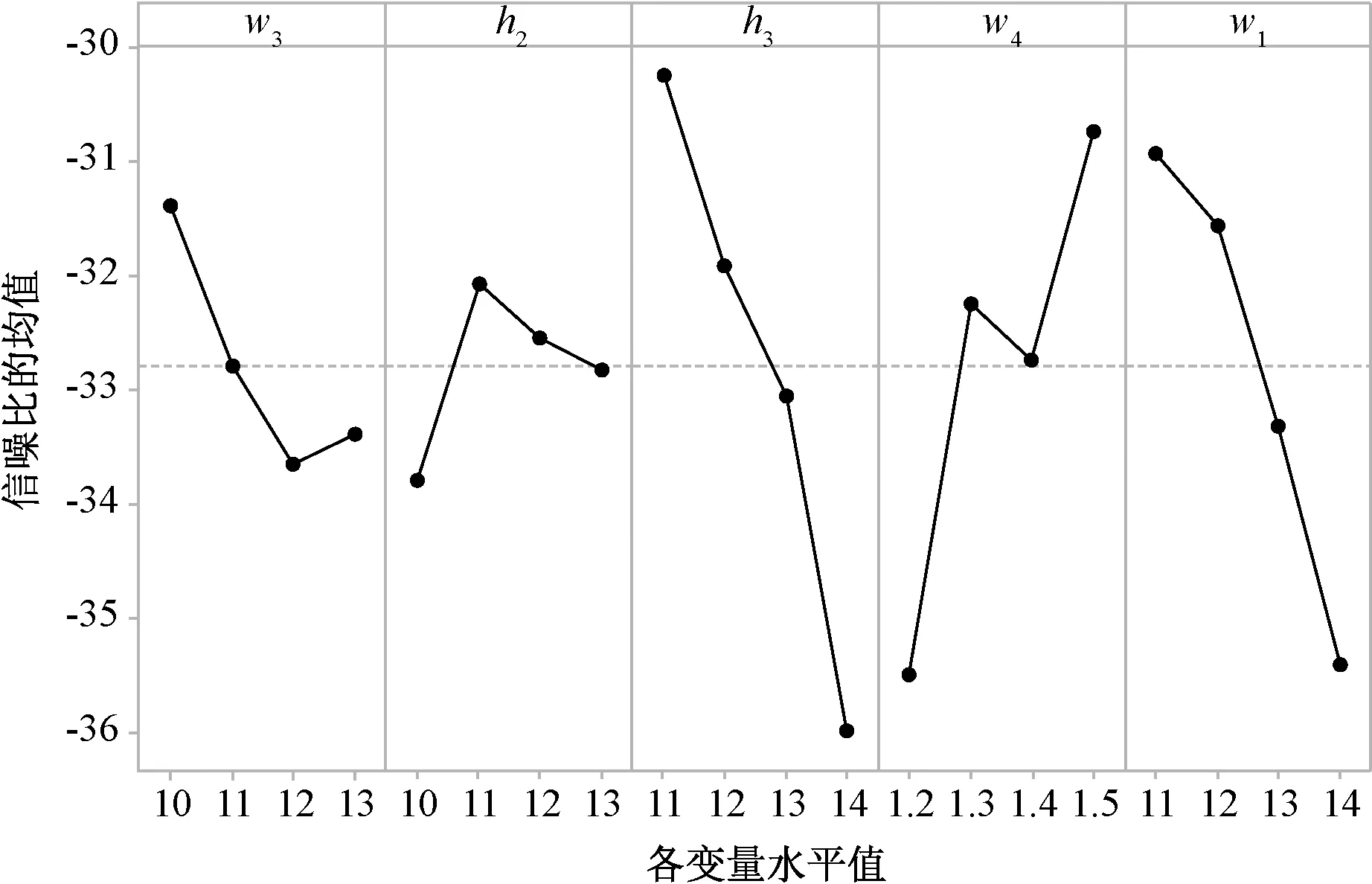
圖5 第二組參數推力波動信噪比

圖6 第二組參數平均推力信噪比

表5 第二組參數方差分析

由圖4、圖5和表3可以看出，h3對平均推力有顯著影響，而h3、w1和w4對推力波動有顯著影響，因此將h3、w1和w4確定為優化變量。根據圖4和圖5的信噪比分析結果，取h2=11 mm,w3=10 mm。

綜上，根據對兩組參數的敏感性分析結果，確定h3、w1、w2、和w4共4個結構參數為優化變量。

3 構建響應面模型

響應面模型是一種數學建模優化和綜合實驗設計方法，可以有效減少實驗次數，準確分析設計變量之間的相互作用。Box-Behnken法是響應曲面設計中常用的一種設計方法。采用Box-Behnken法進行實驗設計時，每個因子取3個水平的值，分別為設計變量優化區間的中心值、上限和下限值。表6為各個優化變量的水平值。

表6 設計變量水平值

根據Box-Behnken法的實驗設計原則，建立一個關于4個變量的正交實驗矩陣，共需要進行27次實驗。通過有限元分析，計算出每次實驗的平均推力和推力波動。正交實驗矩陣和優化目標的實驗結果如表7所示。

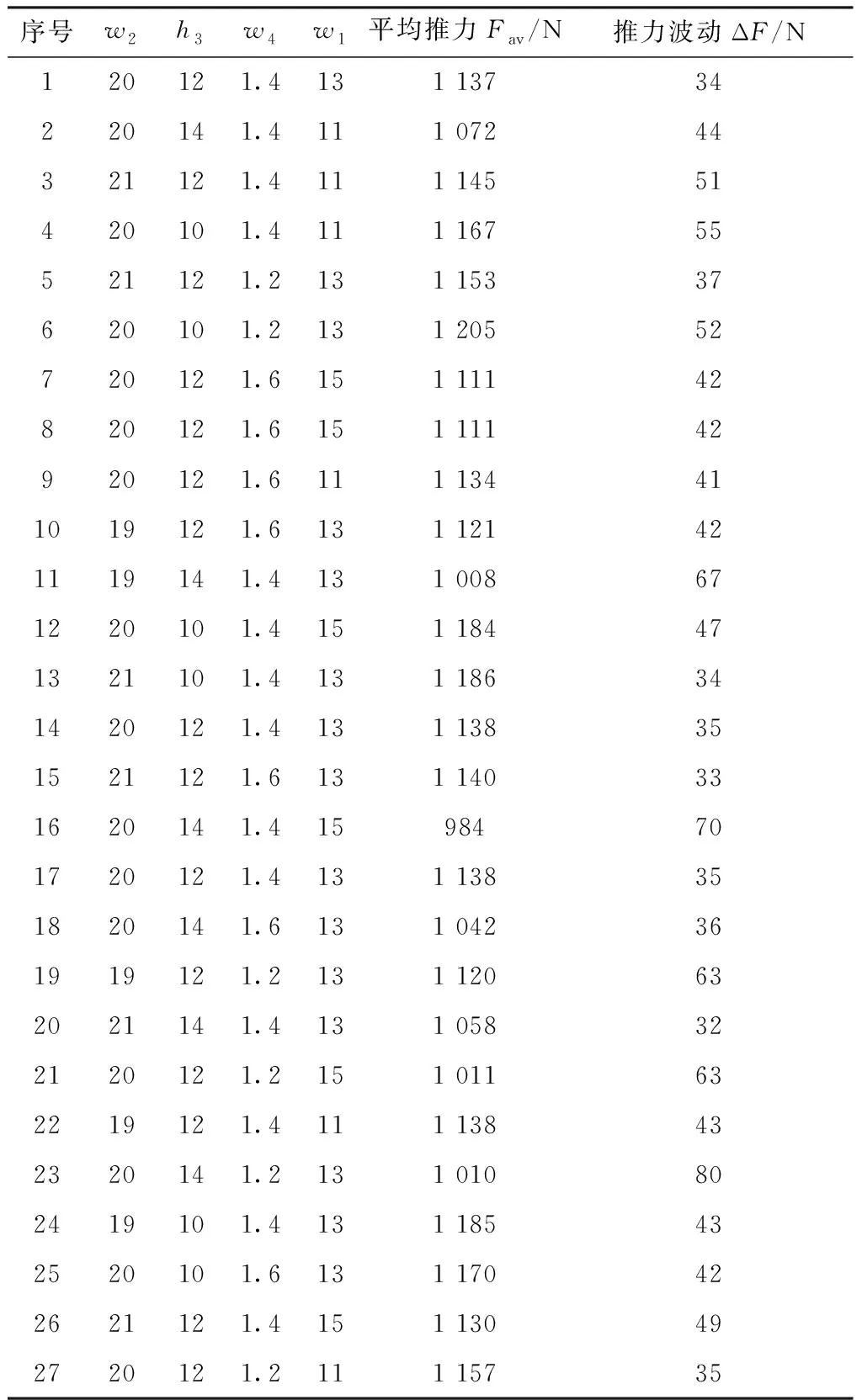
表7 正交實驗矩陣及實驗結果

根據表7的正交實驗矩陣和有限元分析得到的結果，對優化目標進行表面響應分析。通用的二階響應面模型如下式[15]：

(1)

式中：G(t)為響應值；a0、ai、aj為回歸系數；ti、tj為兩個不同的優化變量；ε為擬合誤差。

對表7中的數據進行多元二次回歸擬合，即可得到響應面的數學模型。TPMLM平均推力的擬合回歸方程：

f1=400+12.42w2+132.1h3-699w4+

41.9h3w4-6.56h3w1+76.9w4w1

(2)

TPMLM推力波動的擬合回歸方程：

f2=-750+52.5w2+30.5h3+64w4+

3.37w2h3+16.2w2w4-3.25w2w1-

19.37h3w4+2.125h3w1-15w4w1

(3)

4 多目標算法尋優

TPMLM各個結構參數之間存在相互作用，會使得優化目標不能同時達到最優。采用多目標遺傳優化算法,以最大的平均推力、最小推力波動為目標進行多目標優化求解，數學模型可以表示：

(4)

式中：f1(x)為電機的平均推力函數；f2(x)為電機的推力波動函數；f3(x)為一個磁極用磁量的函數；xil和xih分別為第i個變量的最小值和最大值；w1、w2、w4和h3參數的取值范圍：

通過多目標遺傳優化算法求解，獲得Pareto前沿，如圖7所示。

圖7 Pareto前沿圖

從Pareto解集中選擇一組解A為TPMLM最優參數組合，如表8所示。

表8 最優參數組合

5 電機優化前后性能對比

利用有限元軟件Magnet對表8參數組合的TPMLM電磁模型進行有限元分析。圖8為優化前后TPMLM穩定運行后電機的推力波形，表9為TPMLM的優化結果。

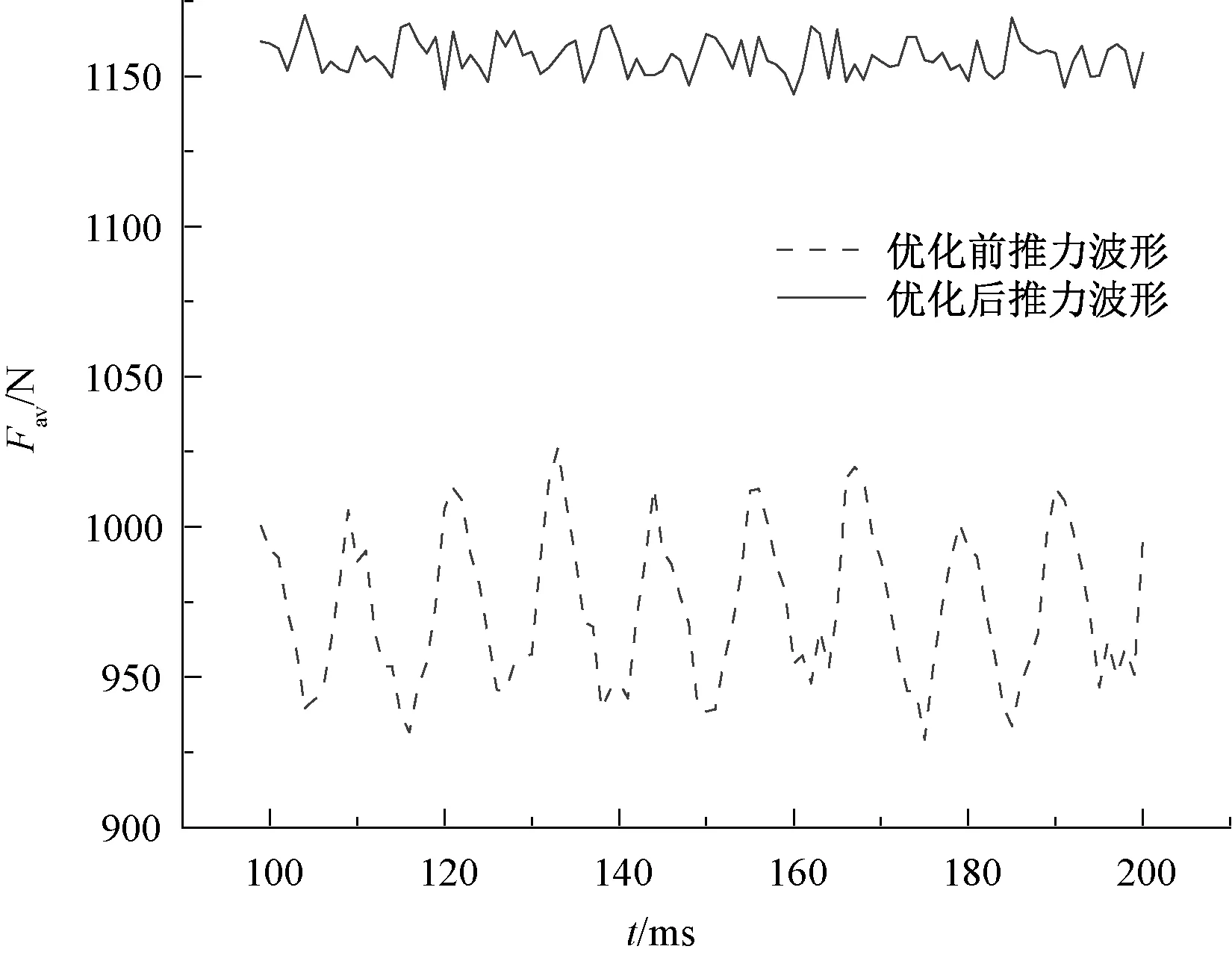
圖8 優化前后推力波形

表9 優化前后TPMLM性能對比

從圖8中可以看出,優化前電機的平均推力約為975 N,推力波動約為97 N;優化后電機的平均推力約為1 157 N，推力波動約為26 N。優化后電機的平均推力提高了18.67%，推力波動降低了73.20%,經過優化后，電機用磁量減小了22.67%。顯然，表8中的參數組合可以提高TPMLM的推力，降低推力波動。

6 結 語

本文對9槽10極TPMLM進行了優化設計，以推力和推力波動為優化目標，選取TPMLM的8個結構參數為優化變量。基于田口法的參數敏感性分析顯示，定子齒部寬度和磁極厚度對電機推力有顯著影響，定子齒部寬度、氣隙寬度、磁極寬度和磁極厚度對推力波動有顯著影響。結合響應面法建立TPMLM平均推力和推力波動關于定子齒部寬度、氣隙寬度、磁極寬度和磁極厚度的二階響應面模型，采用多目標遺傳優化算法對該響應面模型進行求解，獲得最優參數組合。有限元仿真結果表明，與原始電機相比，優化后TPMLM的平均推力提高了18.67%，推力波動降低了73.20%，用磁量減小了22.67%，說明求得的最優參數組合可以有效提升TPMLM的推力特性，也說明了優化方法的可行性與有效性。