一類張量方程的可解性及其最佳逼近問題 ①

代麗芳， 梁茂林

天水師范學院 數學與統計學院， 甘肅 天水741001

張量是數值多重線性代數的主要研究對象， 其在量子力學、 心理測量學、 化學計量學、 信號處理、 高階統計等領域有重要應用[1-3]． 張量是向量和矩陣的高階推廣， 它的許多性質與矩陣情形類似， 但也有很大不同[4]． 張量相關問題的研究要比矩陣情形復雜得多． 目前， 在張量分解、 張量的低秩逼近、 張量互補問題、 張量特征值問題和張量方程等方面已有諸多研究成果[4-9]． 本文考慮基于Einstein積[10]的一類張量方程的求解問題．

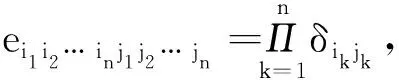
若張量A=(ai1i2… imj1j2… jn)∈CI1×I2×…×Im×J1×J2×…×Jn，B=(bj1j2… jnk1k2… kp)∈CJ1×J2×…×Jn×K1×K2×…×Kp， 則它們的Einstein積A*nB為I1×I2×…×Im×K1×K2×…×Kp-維張量， 依據文獻[7]定義其元素為

進一步， 設張量S=(ai1i2… imj1j2… jn)，T=(bk1k2… kml1l2… ln)且S，T∈CI1×I2×…×Im×J1×J2×…×Jn， 則其內積定義為

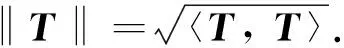
定義1設張量A=(ai1i2… imj1j2… jn)∈CI1×I2×…×Im×J1×J2×…×Jn， 則其共軛轉置AH定義為

若張量A∈CI1×I2×…×Im×I1×I2×…×Im滿足條件AH=A， 則稱之為Hermitian張量．

若定義1中A是實張量， 則共軛轉置退化為轉置[7]． 值得一提的是， 最新的研究發現， Hermitian張量在量子糾纏中有實際應用[11]． 本文考慮張量方程

A*nX=B

(1)

的Hermitian解， 這里A，B∈CP1×P2×…×Pm×I1×I2×…×In為已知張量，X∈CI1×I2×…×In×I1×I2×…×In為未知的Hermitian張量． 張量方程(1)在控制系統、 連續力學等領域有實際應用[7，11]． 例如， 對于2-維泊松方程

Ω={(x，y)|0≤x，y≤1}， 利用中心差分格式， 可以離散為張量方程[7]

A*2U=F

(2)

這里張量A∈RN×N×N×N的非零元為

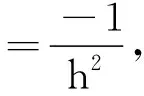
F∈RN×N， 對于沒有約束條件的張量方程(1)， 文獻[7]引入了張量逆的概念， 得到了它的最小二乘解． 進一步， 作為張量逆的推廣形式， 文獻[12]提出了張量的Moore-Penrose廣義逆， 并討論了張量方程(1)的可解性及其通解形式．

在圖像處理等領域的應用中， 考慮方程解的特殊結構是降低算法復雜度的重要途徑[13]， 但是對于帶有約束條件的形如方程(1)的張量方程求解問題尚無研究． 借助張量的Moore-Penrose廣義逆的性質， 我們將建立張量方程組(1)有Hermitian解的充要條件， 并得到有解時的一般解表達式． 進一步， 將考慮張量方程(1)約束下的張量逼近問題．

(3)

其中Θ表示張量方程(1)的所有Hermitian解的集合．

1 主要結果及證明

為了研究Hermitian張量約束下的張量方程(1)的求解問題， 我們首先引入如下引理， 這對得出本文的主要結果是十分重要的．

引理1[19]設F∈CI1×I2×…×Im×J1×J2×…×Jn，G∈CK1×K2×…×Kp×L1×L2×…×Lq，E∈CI1×I2×…×Im×L1×L2×…×Lq， 則張量方程F*nZ*pG=E有解當且僅當F*nF+*mE*qG+*pG=E， 此時它的通解為

Z=F+*mE*qG++Y-F+*mF*nY*pG*qG+

其中張量Y∈CJ1×J2×…×Jn×K1×K2×…×Kp是任意的．

引理2設張量A，B∈CP1×P2×…×Pm×I1×I2×…×In， 則張量方程(1)有Hermitian解的充要條件為張量方程組

(4)

有一般解．

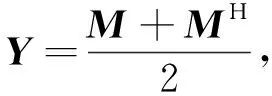
由引理2可見， 求解張量方程(1)的Hermitian解等價于求解張量方程組(4)的一般解． 基于此， 我們得到如下定理．

定理1設張量A，B∈CP1×P2×…×Pm×I1×I2×…×In， 則張量方程(1)有Hermitian解的充要條件為

A*nBH=B*nAH，A*nA+*mB=B

(5)

此時它的一般解為

(6)

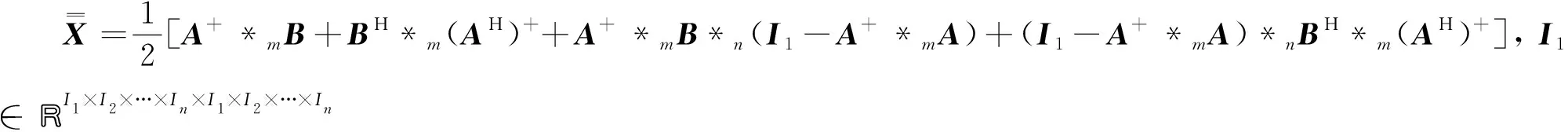
證根據張量Moore-Penrose廣義逆的性質和引理1可知， 張量方程(1)有解的充要條件為

A*nA+*mB=B

(7)

此時

X=A+*mB+(I1-A+*mA)*nZ

(8)

這里Z∈CI1×I2×…×In×I1×I2×…×In為任意張量． 當式(7)成立時， 結合式(4)可知A*nBH=B*nAH， 即知式(5)成立．

進一步， 將式(8)代入式(4)的第二個方程X*nAH=BH并整理得

(I1-A+*mA)*nZ*nAH=BH-A+*mBnAH

這是關于變量Z的張量方程． 在條件(7)成立時， 該方程總是有解的， 且由引理1知其一般解為

(9)

其中W∈CI1×I2×…×In×I1×I2×…×In為任意張量． 將式(9)代入式(8)可得

結合引理2的證明過程可得式(6)成立． 命題得證．

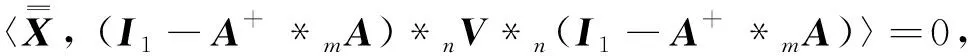
接下來考慮張量的最佳逼近問題(3)． 首先引入如下引理．

引理3[19]設E∈CI1×I2×…×Im×J1×J2×…×Jn，F∈CI1×I2×…×Im×I1×I2×…×Im，G∈CJ1×J2×…×Jn×J1×J2×…×Jn且滿足

F*mF=F=FH，G*nG=G=GH

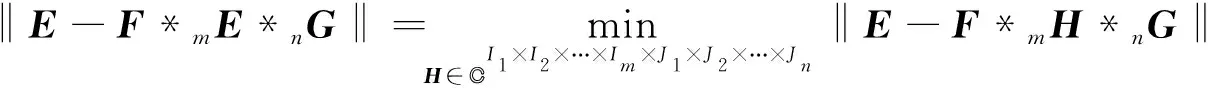
根據引理3， 我們可以證明張量逼近問題(3)的解是唯一的， 并給出解的具體形式．

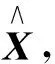
(10)

成立， 此時

(11)

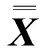
證當定理1中的條件(5)成立時， 張量方程(1)的解集合Θ是非空的， 且容易驗證它是一個閉凸集， 這說明最佳逼近問題(3)有唯一解． 由式(6)和式(3)可得

(12)

因為I1-A+*mA為正交投影張量， 故滿足引理3中的假設條件， 從而有

(13)

當且僅當

(14)

由式(12)和式(13)可得式(10)， 而式(6)和式(14)說明最佳逼近問題(10)的唯一解為

(15)

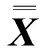
2 數值試驗

本節通過數值例子驗證所得結論的可行性． 接下來的所有實驗數據均是通過配置了Inter(R) Core(TM) i5-4200M CPU與4.00 G內存的電腦上的MATLAB軟件編程實現， 其中張量積的運算用到了張量工具包[20]．

例考慮離散的2-維泊松方程的Hermitian解， 即張量方程(2)， 這里取張量F=eyes(N，N)為單位張量． 另外， 給定張量U0∈RN×N隨機產生， 即U0=randn(N，N)， 容易驗證， 已知張量A和F滿足定理1中的條件(5)， 故相應的張量逼近問題

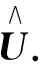
圖1 給定張量及最佳逼近解

3 總結

本文考慮了基于Einstein積的張量方程A*nX=B關于Hermitian張量X的可解性問題． 利用張量Moore-Penrose廣義逆的性質， 得到了上述問題有解的充要條件， 并得到了它的一般解表達式． 另外， 對于任意給定張量， 在假定上述條件成立時， 討論了相應的張量最佳逼近問題， 證明了解的唯一性， 并得到了它的具體表達式． 最后給出實際應用實例驗證了本文所得結果的可行性， 這些結果對張量相關理論的完善具有重要意義．