基于L曲線方法的Lasso正則化參數選擇 ①

吳煒明， 王延新

1.寧波工程學院 理學院， 浙江 寧波 315211； 2.安徽工業大學 商學院， 安徽 馬鞍山 243032

大數據時代已經到來， “數據”貫穿了生活的方方面面， 在各行各業中都起著舉足輕重的作用． 各個領域為了挖掘潛藏的數據價值， 對已有數據進行分析建模， 但同時也面臨著真實場景過于復雜， 易出現高維數據的情況． 在變量維數p遠大于樣本量n的情況下， 傳統低維統計分析方法往往顯得力不從心． 首先模型的準確性難以得到保證， 其次在解釋變量大量增加的情況下， 模型對于問題的可解釋性變差， 分析的焦點被模糊， 并且在高維變量情況下， 模型的復雜度提高， 計算量增加， 存在一定的求解困難． 因此， 在建模過程中， 變量選擇顯得尤為重要．

高維數據變量選擇最常用的方法是基于罰函數的正則化方法[1]， 它可以同時進行變量選擇和參數估計． 稀疏正則化方法的一般框架為

(1)

其中：l(β)為損失函數，pλ(·)為罰函數，λ為正則化參數． 常用的正則化方法有Lasso[2]，adaptive Lasso[3]，relaxed Lasso[4]，SCAD[5]，MCP[6]等． 在實際應用中， 上述方法的正則化參數λ的調節是非常重要的， 正則化參數λ的選擇決定了模型的性能． 目前常采用CV(交叉驗證)[7]， GCV(廣義交叉驗證)[8]， AIC(赤池信息準則)[9]，BIC(貝葉斯信息準則)[8]等多種準則選擇正則化參數λ， 但是每種方法都有各自的優缺點． CV方法的預測誤差小， 但計算量龐大， 而且沒有完整理論推導， 且解釋性較差． GCV方法容易產生過擬合現象[8]， 從而不滿足變量選擇的一致性要求． AIC準則可以權衡估計模型的復雜度和模型擬合數據的優良性， 但也易出現過擬合現象． BIC準則選擇的模型更加接近于真實模型， 但是它只考慮了變量選擇， 參數估計的效果不一定好． Hansen[10]針對嶺回歸問題提出最優化參數選擇的L曲線法． L曲線方法簡單易行， 不受模型誤差方差的影響， 但L曲線方法不一定適用于Lasso正則化參數的選擇．

鑒于以上原因， 本文運用L曲線的思想， 提出一種新的L曲線準則(LC)選擇Lasso正則化參數． 通過數值模擬， 比較CV，GCV，BIC與LC在Lasso方法中模型選擇和參數估計的效果． 最后將該方法運用在實際數據中， 分析探討2019年186個國家經濟自由指數的影響因素．

1 Lasso估計原理與方法

1.1 Lasso估計

考慮線性模型：

y=Xβ+σε

(2)

其中：y=(y1，y2， …，yn)T為響應變量；X=[x1，x2， …，xp]∈Rn×p為解釋變量所組成的樣本數據，xj=(x1j，x2j， …，xnj)T，j=1，2，…，p為解釋變量；β=(β1，β2， …，βp)T為線性方程的回歸系數；ε=(ε1，ε2， …，εn)T為隨機誤差， 并且εi服從均值為0， 方差為1的獨立同分布．

1996年， 文獻[2]提出了Lasso方法， 通過對回歸系數的L1范數進行懲罰來壓縮回歸系數， 并使絕對值較小的回歸系數被自動壓縮為0， 從而同時實現參數估計和變量選擇， 基于線性回歸的Lasso模型為

(3)

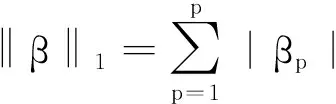
1.2 參數選擇方法

正則化參數λ的選擇決定了模型的性能， 因此參數λ的選擇至關重要． 目前Lasso方法常通過CV，GCV，AIC，BIC等多種方法來確定參數．

1) CV方法是一種無假設， 可以直接進行參數估計的變量選擇的方法． 其思想是在給定樣本中， 拿出大部分樣本進行建模(訓練集)， 留小部分樣本用建立的模型進行預測(測試集)， 并計算小部分樣本的預測誤差， 記錄誤差平方和． 它的優點是預測誤差小， 但是計算量龐大， 而且沒有完整的理論依據推導， 解釋性較差． CV方法的公式如下：

(4)

2) GCV計算過程簡單， GCV具體形式為

(5)

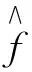
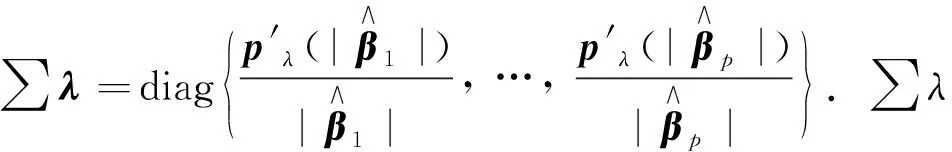
但文獻[8]指出GCV方法容易產生過擬合現象， 即在參數選擇時，λ容易過小， 則非零β數量就會過多， 造成模型的過擬合， 從而不滿足變量選擇的一致性要求．

3) 基于BIC準則的正則化參數選擇大致對應于在適當的貝葉斯公式中最大化選擇真實模型的后驗概率， BIC準則定義如下：

(6)

理論上已經證明BIC準則滿足模型選擇的一致性要求， 由BIC準則選擇的模型更加接近于真實模型， 但是它只考慮了變量選擇， 參數估計的效果不一定好． 在高維情形下的BIC準則可見文獻[10]．

2 基于LC準則的正則化參數選擇

2.1 嶺回歸中的L曲線準則

嶺回歸模型[11]為：

(7)

其中λ≥0為正則化參數． 嶺估計的罰函數是L2范數， 不能把系數壓縮到零， 因此不能產生稀疏解． 嶺參數的選擇會在很大程度上影響估計的結果．

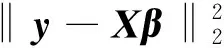
(8)

其中：ρ表示殘差范數，η表示解范數， ′表示對參數λ求導．

2.2 Lasso中的L曲線準則

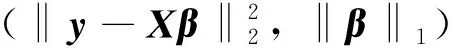
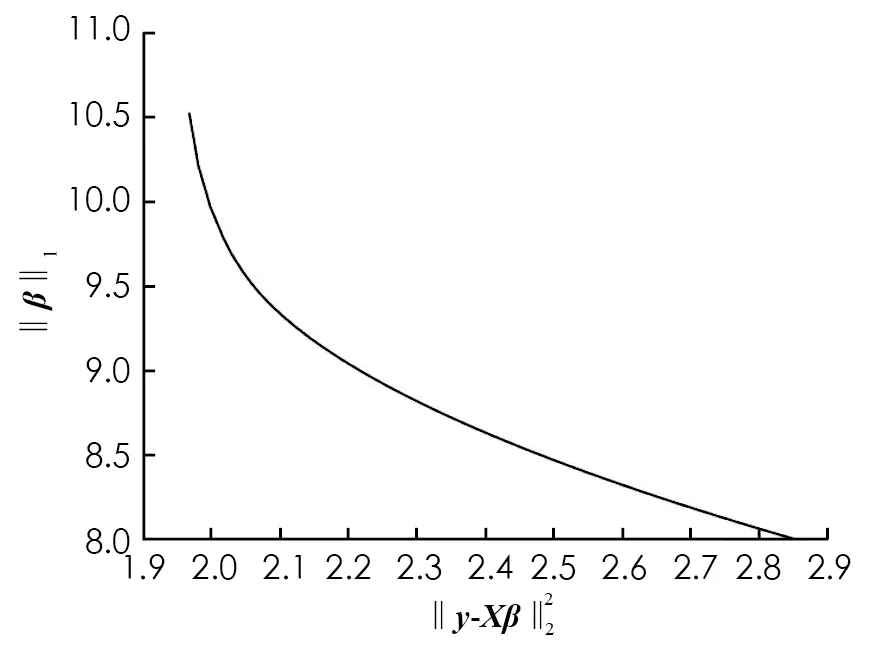
圖1 Lasso正則化的L曲線

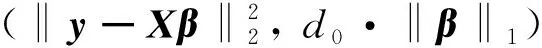
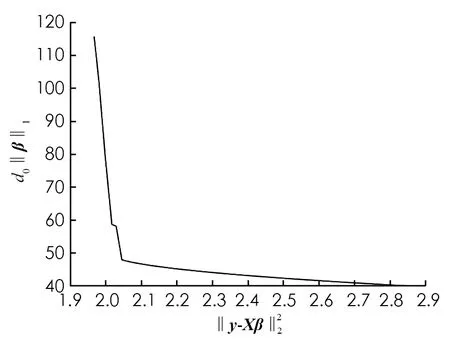
圖2 Lasso正則化L曲線

3 數值模擬與實際應用

3.1 數值模擬

本節通過數值模擬， 來比較在CV，GCV，BIC，LC下通過Lasso正則化方法進行變量選擇以及參數估計．

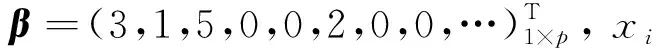
為比較估計精確性， 需計算模型誤差

(9)

通過多次的重復試驗， 用以下指標來評價不同參數選擇方法下Lasso估計的模型性能． “MME”表示模型誤差ME的中位數； “SD”表示模型誤差ME的標準差； “C”表示100次重復實驗中非零系數被正確估計為非零個數的均值； “IC”表示100次重復實驗中零系數被錯誤估計為非零個數的均值； “Underfit”表示欠擬合， 即在100次模擬實驗中將非零系數錯誤估計為零的比例； “Correctfit”表示正確擬合， 即在100次模擬實驗中將非零系數正確估計為非零的比例； “Overfit”表示過擬合， 即100次模擬實驗中選擇了所有重要變量并且包含了非零系數的比例．

表1和表2分別展示了低維數據和高維數據兩種情況， 在不同的隨機誤差水平下， 運用多種變量選擇的方法進行Lasso估計． 從參數估計誤差角度來看， Lasso估計在LC準則下誤差比CV方法選擇的模型誤差小， 但是比BIC準則選擇的模型誤差大， 即Lasso估計在LC準則下參數估計的效果介于CV方法和BIC準則之間． 從模型的稀疏性角度來看， Lasso估計在LC準則下選擇模型較CV，GCV，BIC具有更高的正確擬合比例， 具有更低的過擬合比例， 即LC準則下的Lasso估計能夠選擇較稀疏的模型． 從變量選擇的一致性角度來看， Lasso估計在LC準則下的系數估計效果比CV，GCV，BIC都好， 即LC準則下Lasso估計所選擇的變量的一致性較好．

表1 低維數據模擬

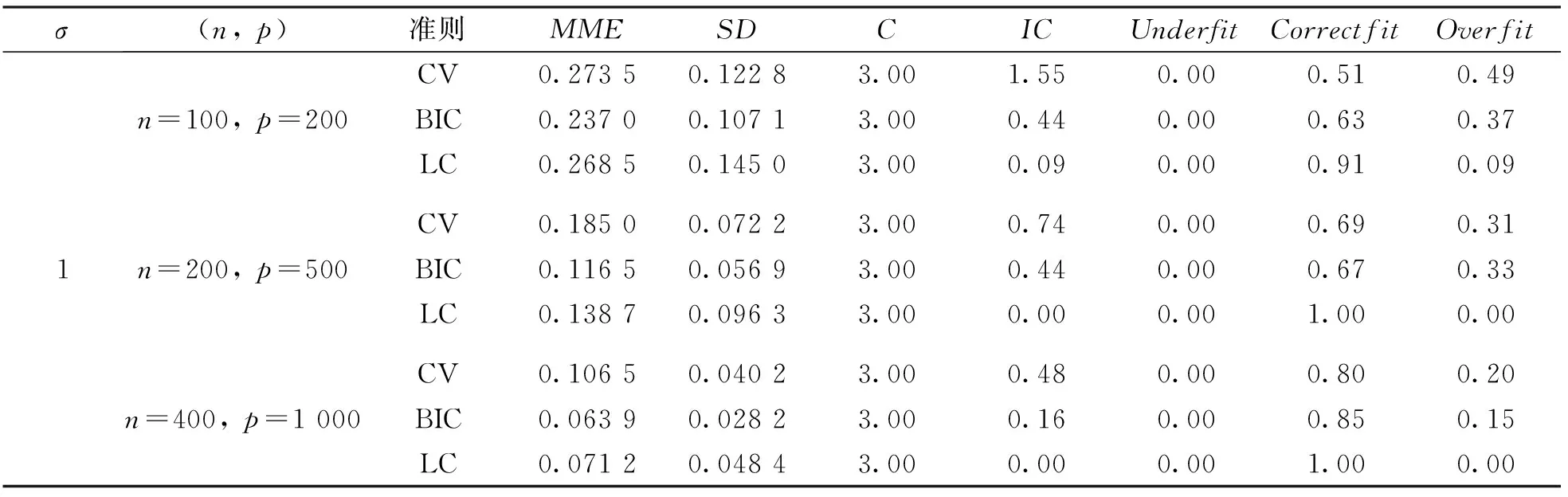
表2 高維數據模擬

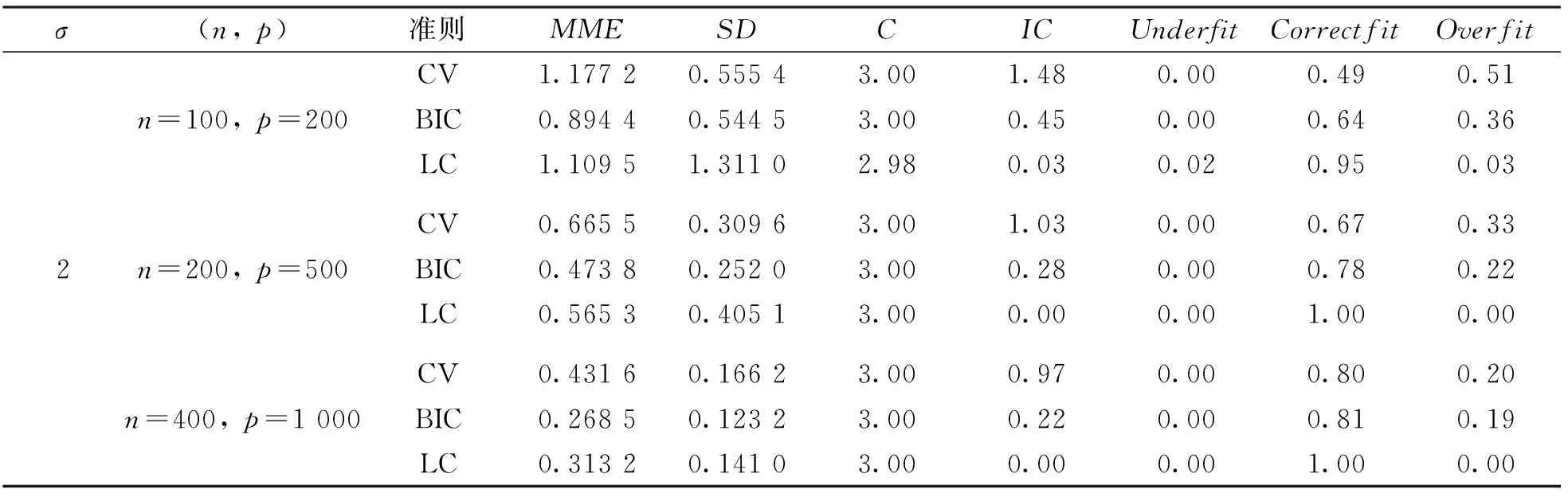
續表2

3.2 實例分析

本節在kaggle平臺下載2019年世界186個國家的經濟自由指數的相關數據， 該數據集共有13個變量， 涵蓋186個國家的12項自由指標， 從財產權到財務自由， 分別為： 財產權X1； 司法效力X2； 政府誠信X3； 稅收負擔X4； 政府支出X5； 財政健康X6； 商業自由X7； 勞工自由X8； 貨幣自由X9； 貿易自由X10； 投資自由X11； 財務自由X12； 經濟自由指數Y． 對數據進行缺失值和異常值處理， 剩下173個國家的樣本數據． 把經濟自由指數作為響應變量， 其余12個變量作為解釋變量， 進行實例分析建模．

通過分析， 從表3可以看出， 經濟自由指數與其余各因素呈現較強的線性關系， 即有線性模型：

(10)

其中：yi表示第i個國家的經濟自由指數(得分)，xij為第i個國家的第j個變量，εi是均值為0， 方差為σ2的隨機誤差項．

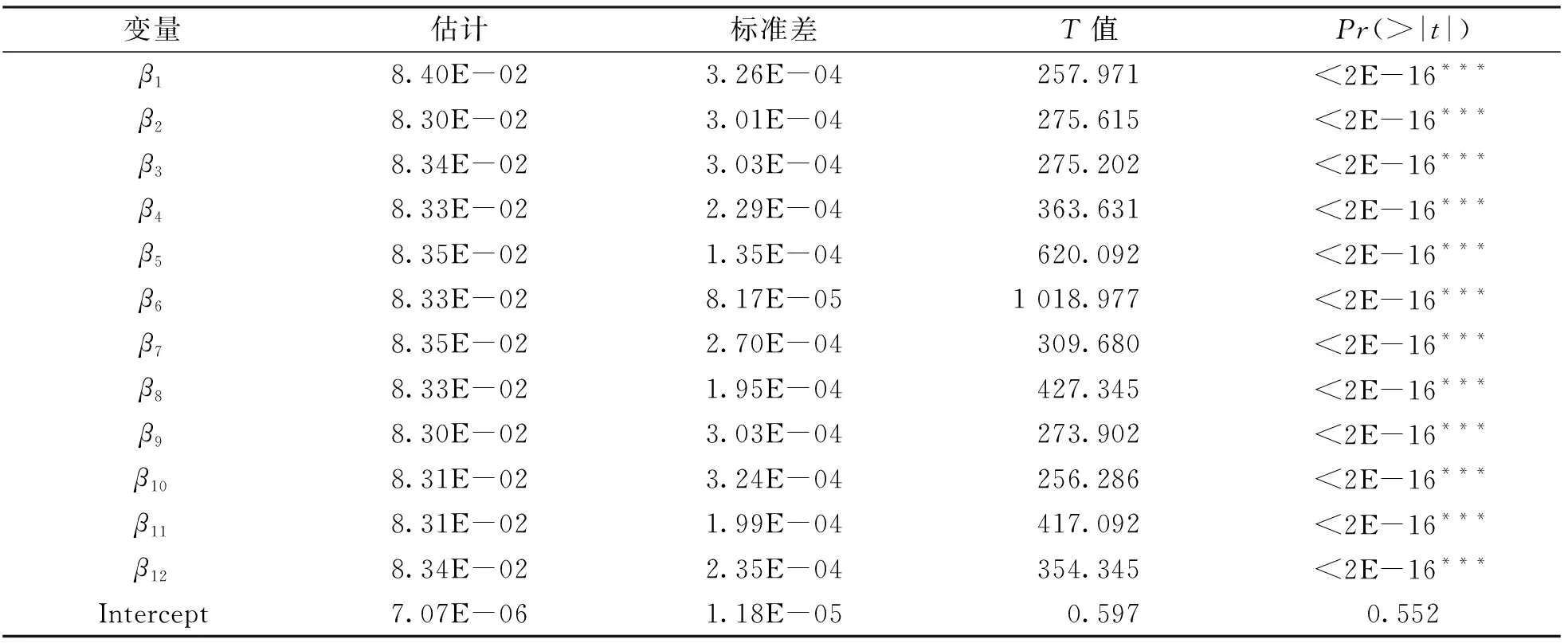
表3 線性模型結果

利用OLS(最小二乘估計)，CV，GCV，BIC和LC下的Lasso估計對該數據進行分析． 變量選擇結果如表4所示． 從變量選擇的數量來看， 最小二乘估計 (OLS) 選擇了所有的變量， CV下的Lasso罰估計也選擇了全部12個變量， 沒有達到變量選擇的目的； GCV和BIC準則下的Lasso估計分別選擇了11個和12個變量； 通過LC準則的Lasso罰估計選擇了3個重要變量， 分別為X3，X4，X5， 模型也更為稀疏．

4 結論

本文討論了Lasso正則化方法在變量選擇和參數估計中的應用， 針對Lasso正則化提出了LC準則， 從而更好地確定在不同數據情況下的最優正則化參數． 數據模擬和實際應用的結果都表明， Lasso估計在LC準則下能夠選擇較稀疏的模型， 且有較高的概率選擇與真實情況相吻合的模型， 模型選擇效果好． 另外LC準則下的模型的誤差較小， 參數估計效果好． 本文的LC準則同樣可以推廣到非線性模型中．

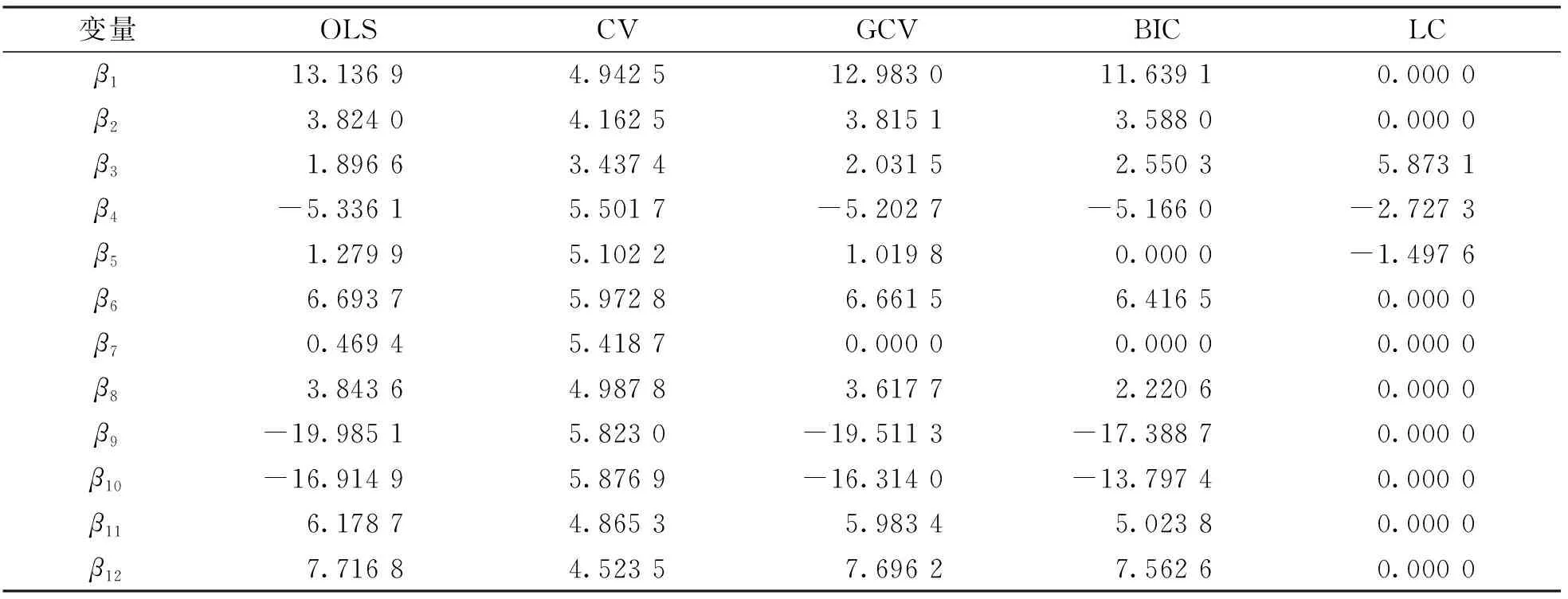
表4 不同方法下的參數估計結果