訂單可拆開加工的兩代理分批調(diào)度問題 ①
劉甲玉, 耿志超
1.河南交通職業(yè)技術學院 公共基礎教學部, 鄭州 450001; 2.鄭州大學 數(shù)學與統(tǒng)計學院, 鄭州 450001
現(xiàn)代生產(chǎn)企業(yè)為提高生產(chǎn)效率普遍采用分批加工模式, 即在多個車間或機器上同時加工一定數(shù)量的產(chǎn)品或零部件. 比如, 在半導體加工廠里集成電路板耐熱測試的熔斷工序[1]中, 測試容器可以同時處理大量的電路板. 關于分批調(diào)度的研究已有大量結果[2-3]. 本文關注如下的實際生產(chǎn)情形: 某加工廠接到了來自兩個客戶的多個訂單, 每個訂單對應于不同類型的產(chǎn)品或同一類型產(chǎn)品的不同款式, 每個訂單中的產(chǎn)品數(shù)量不同; 兩個客戶對其訂單有不同的期望和要求, 其中一個客戶期望為其各個訂單支付的加工費用均衡化(本文用最小化最大加工費用表示), 而另一客戶期望其各個訂單均盡早交付(本文用最小化完工時間之和表示). 每個訂單均可分拆成多個部分并連續(xù)地在相鄰的批中加工.
文獻[4-6]研究了訂單可拆分加工的分批調(diào)度問題, 但均是針對單個代理情形, 而本文將在兩個競爭代理的背景下研究相關問題.
多代理排序問題最早是由文獻[7-8]提出的. 針對兩個代理的多個不同的目標函數(shù)組合, 文獻[7]研究了兩個代理的目標函數(shù)的加權和問題, 設計了多項式時間算法并證明了NP難性; 而文獻[8]研究了限制問題, 即在滿足不超過一個代理目標函數(shù)的門檻值的條件下, 使另一個代理的目標函數(shù)最小化, 同時也研究了幾個Pareto 優(yōu)化問題, 設計的算法能夠在多項式時間內(nèi)枚舉所有Pareto 最優(yōu)點, 并為每個Pareto最優(yōu)點找到一個對應的Pareto最優(yōu)解. 文獻[9]中將多代理模型分類為: 競爭代理模型(CO)、 非不交代理模型(ND)、 Interfering代理模型(IN)、 多指標代理模型(MU), 并對多代理排序問題的研究結果進行了詳細的綜述. 文獻[10]研究了單機、 工件有到達時間并允許中斷且具有多個瓶頸指標的情形下的相關多代理排序問題, 給出了多項式時間算法或證明了NP難性. 該論文在求解多指標折中排序的方法上有巨大創(chuàng)新. 文獻[11-12]研究了在滿足其中一個代理的最大費用不超過給定常數(shù)的條件下最小化另一個代理的總誤工量的排序問題, 給出了擬多項式時間算法. 文獻[13] 研究了最小化總的加權誤工量的多代理折衷指標排序問題, 證明了當代理的個數(shù)是變量時問題是強NP難的, 當代理的個數(shù)是固定值時問題是NP難的, 并設計了擬多項式時間算法和完全多項式時間近似方案. 更多相關工作可參見文獻[14-16].
1 問題描述
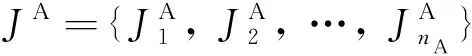

(1)

(2)
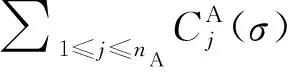
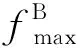
2 算法設計與分析
2.1 NP難性

1) ESP問題. 給定2m+1個正整數(shù)a1,a2,…,a2m和C, 滿足∑1≤j≤2maj=2C, 問是否存在指標集{1, 2, …, 2m}的一個劃分(I1,I2), 使得∑j∈I1aj=∑j∈I2aj=C且|I1|=|I2|?
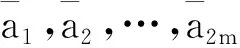
引理1RESP是NP完全問題.

(3)
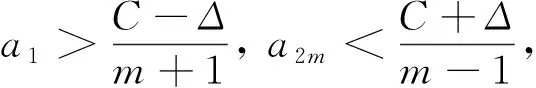
進而, 因a1≤a2≤…≤a2m, 故對任意1≤j≤2m, 有
又由于
因此, 上面構造的實例確實是問題RESP的一個實例.


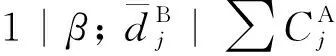

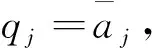

因此,σ是排序?qū)嵗凉M足要求的可行排序.
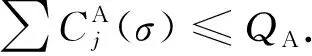
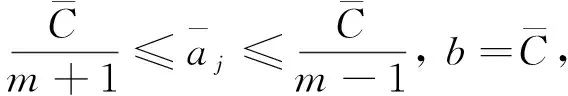
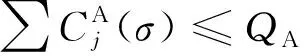
情形2J2m+1被拆分成兩部分, 其中一部分在第一批ψ1, 另一部分在第二批ψ2. 由于來自不同代理的工件不能在同一批中加工, 故其他工件將填滿第三批ψ3和第四批ψ4, 可能會有某個工件被拆分成兩部分, 其中一部分在ψ3, 另一部分在ψ4. 類似情形1中結尾部分的證明, 可得
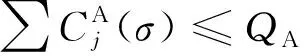
由引理2可直接得到下面的定理.
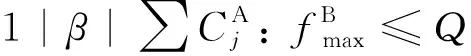
2.2 動態(tài)規(guī)劃算法
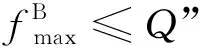

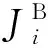
由上述分析可知, 在新排序σ′中, 代理B的所有工件仍然滿足截止日期的要求, 代理A的工件的完工時間之和沒有增加. 因此,σ′也是問題的一個最優(yōu)排序. 接著, 如果σ′仍然不具有引理中描述的最優(yōu)解的結構, 則重復上面的移動操作. 經(jīng)過有限次重復操作后, 將會得到一個滿足條件的最優(yōu)解.

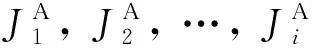
4) 遞歸關系:
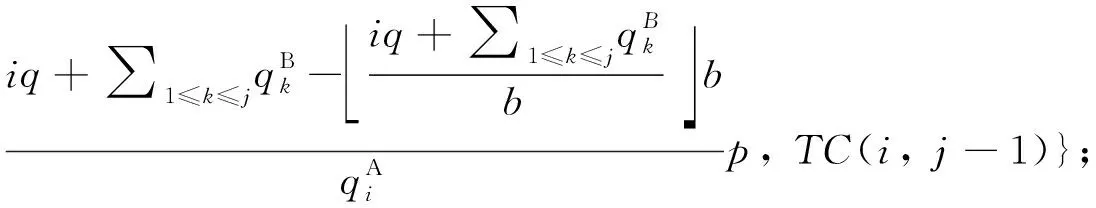
5) 最優(yōu)值為TC(nA,nB), 最優(yōu)解可通過反向追蹤找到.
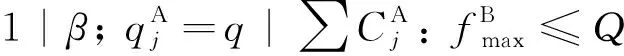
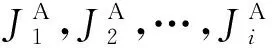
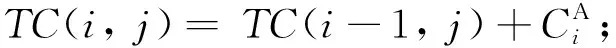
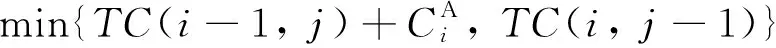
接下來, 分析算法的運行時間. 在DP算法中, 步驟1)對于給定的門檻值Q, 計算代理B的每個工件的截止交貨期, 需要采用二元搜索方法花費O(logQ)時間完成, 于是, 計算代理B的所有工件的截止交貨期共需花費O(nBlogQ)時間; 步驟2)對代理B的工件按截止交貨期由小到大重新標號需要花費O(nBlognB)時間; 步驟3)-5)是動態(tài)規(guī)劃的迭代執(zhí)行過程, 至多需進行nAnB次迭代, 每次迭代可以在常數(shù)時間完成, 于是, 總共花費O(nAnB)時間. 綜合上面的分析, DP算法的運行時間為
O(nAnB)+O(nBlogQ)+O(nBlognB)=O(nAnB+nBmax{lognB, logQ})
3 結論
本文研究了工件可拆分的多代理分批調(diào)度問題, 目標函數(shù)是在滿足不超過一個代理的最大加工費用預算條件下, 最小化另一個代理的工件的完工時間之和. 證明了此問題是NP難的, 并對該問題的一個特殊情形給出了多項式時間算法. 未來, 可進一步研究其他目標函數(shù), 如加權完工時間等問題.

