無標度網絡上一類具有隔離項的時滯傳染病模型研究 ①

趙潤東， 孫梅慈， 劉啟明

陸軍工程大學石家莊校區 軍政基礎系， 石家莊 050003

傳染病歷來是危害人類健康的大敵， 為了遏制疾病傳播， 許多學者通過建立數學模型來研究其傳播過程， 其中主要使用的是“倉室”(Compartment)模型． 1927年， 文獻[1]建立了著名的SIR傳染病倉室模型． 其后， 經過許多學者的不斷研究， 建立了適用不同疾病的傳染病模型， 如SIS[2]， SEIR[3]， SEIRS[4]等．

遏制疾病的傳播， 我們通常采用疫苗接種和隔離兩種方法． 但是針對新出現的傳染病， 疫苗的研發和生產往往需要很長時間， 因此在疾病傳播初期最為有效的方法就是對人群進行隔離[5]． 1995年， 文獻[6]首次在傳染病模型中考慮隔離的影響， 建立了SIQR模型； 2002年， 文獻[7]在隨機網絡傳染病模型中加入隔離項， 建立并研究了SIQS傳染病模型． 上述研究都是基于隨機網絡研究的， 其特點是每個個體是均勻接觸的．

然而， 文獻[8]發現現實中大多數網絡的節點分布符合無標度性(異質性)， 也就是服從冪律分布p(k)=Ck-γ(2<γ≤3)， 因此基于異質復雜網絡來建立模型就更加貼合實際． 2001年， 文獻[9]首次在無標度網絡上對一類SIS傳染病模型進行了研究． 此后， 許多學者開始研究復雜網絡上的傳染病動力學． 另一方面， 現實中許多傳染病當前的傳播狀態會受到過去狀態的影響， 因此， 建立時滯傳染病模型就更具有現實意義， 其中時滯可以用來描述病人的平均感染周期、 潛伏周期、 免疫周期和隔離周期等[10]． 近期許多學者將網絡的無標度性和時滯結合在一起研究傳染病模型， 取得了豐富成果． 2012年， 文獻[11]建立了時滯SEIRS網絡傳染病模型， 其中時滯代表平均免疫周期． 2018年， 文獻[12]建立并研究了時滯SEIR網絡傳染病模型， 其時滯代表疾病的平均潛伏周期． 2019年， 文獻[13]研究了復雜網絡上一類新的時滯SIS模型， 其時滯代表病人的平均感染周期． 但是鮮有人在網絡上用時滯表示隔離周期來建立數學模型對傳染病動力學性態進行研究．

根據以上分析， 本文基于無標度網絡建立一類新的具有時滯的SIQR傳染病模型， 其中時滯代表平均隔離周期． 通過泛函微分方程穩定性理論， 研究了該模型的動力學行為， 得到疾病傳播的基本再生數， 分析了平衡點的全局穩定性， 并通過數值模擬驗證了研究結果的正確性．

1 模型建立

假設總人群的接觸網絡是一個無標度網絡， 一個節點表示一個人， 網絡上的連邊表示人與人之間的接觸． 我們作如下假設：

1) 整個網絡的出生率和自然死亡率分別為A和d， 并且出生的個體都為易感染者． 依據文獻[14]， 添加和刪除節點和邊在網絡中只占很小的比例， 對網絡結構的改變很小， 因此可以假設網絡上的總節點數N是不變的， 是靜態的， 也就是A=d．

2) 網絡上的人分為4類： 易感染者S(Susceptible)、 感染者I(Infected)、 隔離者Q(Quarantine)、 恢復者R(Recovered)． 令Sk(t)，Ik(t)，Qk(t)和Rk(t)分別代表度為k的易感染者、 感染者、 隔離者和恢復者在t時刻的相對密度． 標準化后，Sk(t)+Ik(t)+Qk(t)+Rk(t)=1．

3) 每個易感染者S都有概率λ(k)(與節點的度k有關)被感染者感染， 成為感染者I． 感染者I有概率δ被隔離， 成為隔離者Q． 感染者I同時有概率γ恢復健康， 成為恢復者R． 隔離者Q經過τ時間的隔離治療后， 成為恢復者R．

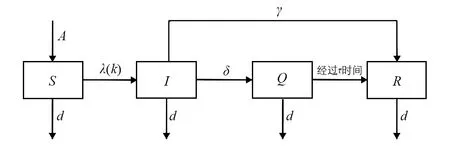
圖1 時滯SIQR模型的倉室框圖

基于以上假設， 可建立SIQR模型的倉室框圖(圖1)， 對應的微分方程系統如下：

(1)

其中λ(k)為感染率， 其形式一般有如下兩種[14]：λk，λc(k)．Θ(t)代表一個度為k的易感染者每次接觸感染者的概率[14]， 其形式如下：

(2)

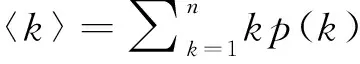
給出系統(1)的初始條件

(3)

其中

由泛函微分方程的基本理論[18]易知在初始條件(3)下， 系統(1)存在唯一解， 并且當t≥0時， 系統(1)存在唯一正解． 同時， 不難得出區域Ω是系統(1)的正向不變集， 本文將在Ω內討論系統(1)的性態．

(4)

2 模型動力學分析

建立模型后， 需得出疾病的基本再生數R0[18]， 即單位病程內一個病人所傳染的人數． 當R0<1時， 一個病人在單位病程能傳染的人數小于1， 疾病將自然消失， 不會流行； 當R0>1時， 一個病人在單位病程能傳染的人數大于1， 疾病將持久存在， 成為流行病．

定理1令

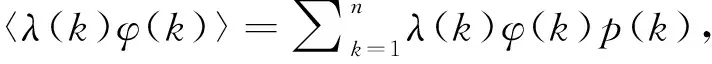
1) 系統存在無病平衡點E0

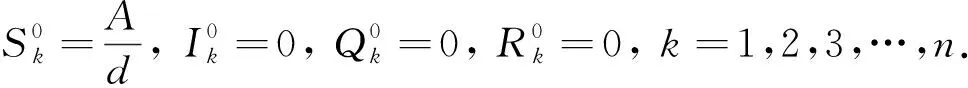
2) 當R0>0 時， 系統(1)存在地方病平衡點E*

證由系統(1)中的方程組， 不難得出系統(1)始終存在無病平衡點E0

接下來， 假設系統存在地方病平衡點E*，

則E*滿足系統(1)

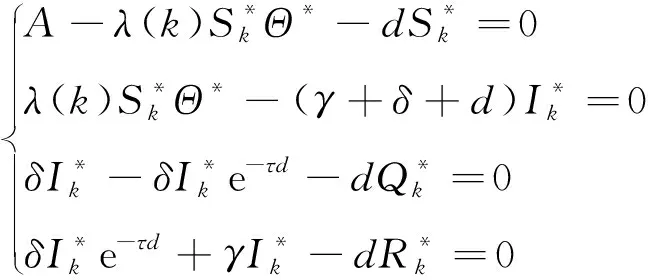
(5)

其中，

(6)

解方程組(5)， 得到

(7)

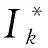
(8)

顯然，Θ*=0是平凡解． 當Θ*≠0時對(8)式兩邊同除以Θ*， 研究函數

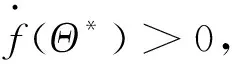
因此， 我們定義基本再生數R0如下

綜合上述分析， 當R0>1時， 系統(1)存在地方病平衡點E*．

注1由R0的表達式得出，R0與出生率A， 感染率λ(k)和非線性傳染系數φ(k)正相關， 與死亡率d， 恢復率γ和隔離率δ負相關．

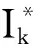
定理2當R0<1時， 系統(1)的無病平衡點E0全局漸近穩定．

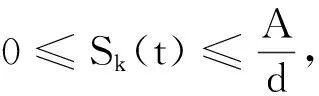
計算V(t)沿系統(1)的導數可得

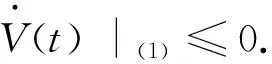
定理3當R0>1時， 系統(1)的地方病平衡點E*全局漸近穩定．

證注意到， 系統(1)中的前兩個方程不涉及Q(t)和R(t)， 由此， 只需考慮如下系統：

(9)

其中

聯合(9)式和(5)式， 得到

考慮如下函數

(10)

U(t)沿系統(9)求導， 得

(11)

定義函數

H(x)=-x+lnx，G(x)=x-1-lnx

注意到當x>0時，G(x)≥0， 當且僅當x=1時， 等號成立． 則(11)式可化為

(12)

考慮如下兩個矩陣

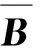
v=(v1，v2， …，vn)=(C11，C22， …，Cnn)

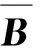
即

(13)

現在定義Lyapunov函數

注3當A=0，d=0，λ(k)=λk，φ(k)=k， 并取時滯τ=ε-1， 時滯微分系統(1)簡化為文獻[22]中的常微分系統(1)． 此時基本再生數的表達式R0=λ〈k2〉·[〈k〉(γ+δ)]-1， 結論與文獻[22]一致．

3 數值模擬

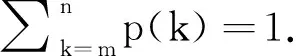
取λ=0.1，A=0.1，d=0.1，τ=3，δ=0.1，γ=0.03， 則R0≈0.774 1<1．I40(t)，I80(t)，I120(t)，I160(t)和I(t)隨時間t的變化趨勢見圖2， 可以看出當R0<1時， 疾病逐漸消失． 取λ=0.2，A=0.1，d=0.1，τ=3，δ=0.1，γ=0.03， 則R0≈1.548 2>1．I40(t)，I80(t)，I120(t)，I160(t)和I(t)隨時間t的變化趨勢見圖3， 可以看出當R0>1時， 疾病持續存在， 并且逐漸趨向到一個穩定值． 圖2和圖3分別驗證了定理2和定理3．

最后， 我們進行參數敏感性分析， 用PRCC(偏秩相關系數)檢測基本再生數R0對于參數的依賴性． 取樣本空間n=1 200， 計算6個影響R0參數的PRCC值． 如圖4所示，λ和A對R0有正影響，d，γ，δ對R0負影響， 而R0對τ不敏感． 圖4驗證了注1 中對R0表達式的說明． 因此， 增大隔離率δ， 提高恢復率γ， 降低感染率λ可以控制疾病傳播．

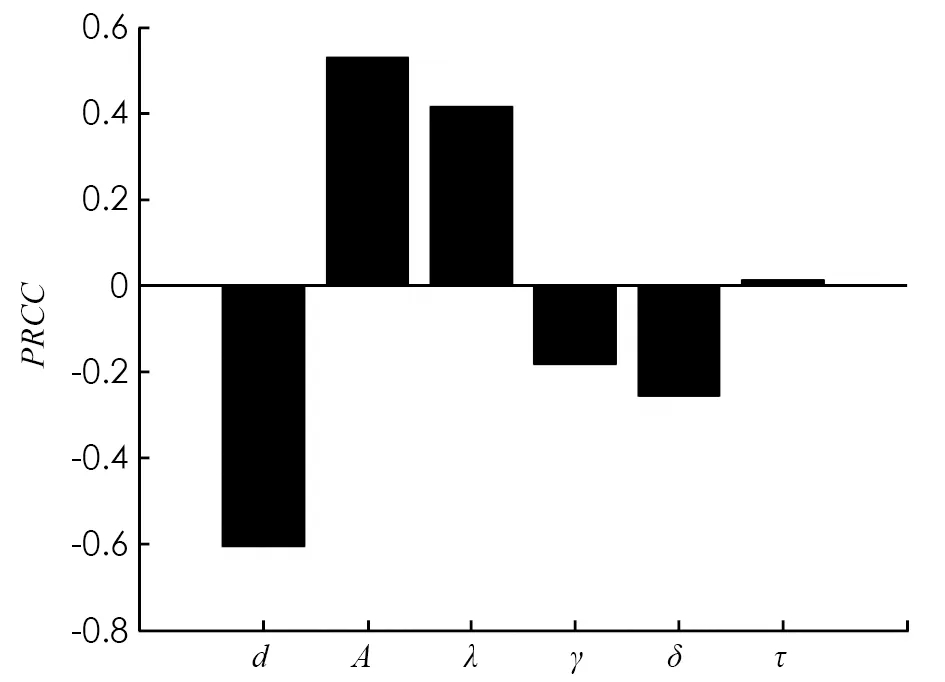
圖4 R0關于不同參數的PRCC值

4 結論

為了研究隔離周期對傳染病的影響， 本文基于無標度網絡建立了具有時滯的SIQR傳染病模型， 其中時滯代表平均隔離周期． 通過微分方程定性與穩定性理論， 得到了疾病傳播的基本再生數． 通過構造Lyapunov函數， 證明了當R0<1時， 無病平衡點是全局漸近穩定的； 當R0>1時， 地方病平衡點是全局漸近穩定的． 最后， 對模型進行數值模擬， 驗證了結論的正確性， 并對不同參數進行了敏感性分析． 研究結果表明隔離周期的長短不影響易感染者和感染者的最終人數， 但是影響隔離者和恢復者的最終人數． 基于R0的表達式以及不同參數的PRCC值， 得出控制疾病傳播的有效方法為增大隔離率， 提高恢復率和降低感染率．