等腰取等三角形幾何不等式研究的若干新結果

劉保乾

（西藏自治區組織編制信息管理中心，西藏 拉薩 850000）

0 引言

當三角形為等腰三角形時取等號的不等式簡稱為等腰取等不等式.說到等腰取等不等式，首先想到的就是Bottema基本不等式[1]

除不等式（1）之外，是否還有其它等腰三角形時取等號的不等式呢？

1995年，楊學枝提出并證明了[2]：在ΔABC中，有關于中線的不等式

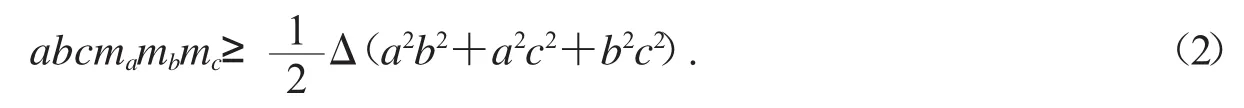
不等式（2）當且僅當三角形為等腰三角形時取等號.注意不等式（2）等價于不等式[3]

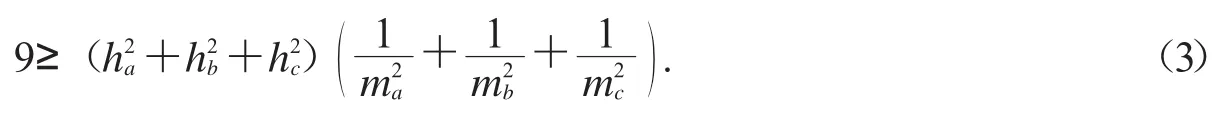
上述不等式雖然是等腰取等的，但它們有一個共同的特點就是，當給不等式兩邊直接平方并分解因式時會出現因式因而我們認為它們是平凡的等腰取等不等式.

真正的不平凡的等腰取等不等式出現于文獻[4]中.文獻[4]中給出了關于三角形中線的不等式

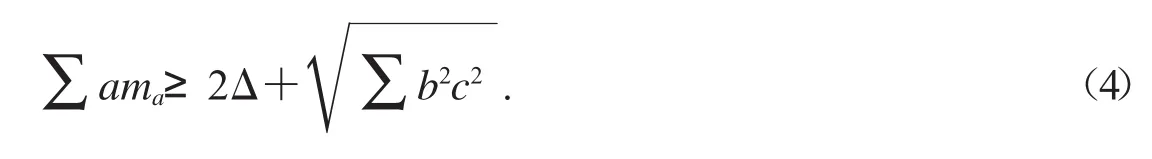
不等式（4）當且僅當三角形為等腰三角形時取等號.像（4）式這種不等式以根式形式出現，取等號條件不能通過簡單的變形或分解因式得到，因而它們是不平凡的.從此以后，等腰取等不等式越來越多地出現在人們的視野中（參閱文獻[5-8]）.本文介紹筆者近幾年在等腰取等不等式研究方面的若干新成果.

以下約定：ΔABC三邊為 a，b，c，半周為 s，角平分線、中線、高分別為 wa，wb，wc、ma，mb，mc和ha，hb，hc，內切圓和外接圓半徑分別為r和R.用∑和∏分別表示循環和與循環積.

1 等腰取等量及其運算性質

在ΔABC中，如果一個對稱表達式當ΔABC為等腰三角形時取值為零或為1，則稱這個表達式是等腰取等量.在等腰取等量中，有兩個特殊的量需要特別注意，一是加強余項，它是指非負的等腰取等量，當三角形為等腰三角形時其取值為零.顯然等腰取等不等式的式差（不等式兩邊的差）構成的量就是一個加強余項.二是加強因子，它是指不小于1的等腰取等量，當三角形為等腰三角形時其取值為1.顯然等腰取等不等式的式商（即不等式兩邊相除）構成一個加強因子.由于當三角形為等腰三角形時加強余項取值為零，故給等腰取等不等式加上或者減去一個加強余項時不等式取等號條件不會變化，利用這個特點可以加強等腰取等不等式.同樣，當三角形為等腰三角形時加強因子取值為1，故給等腰取等不等式某項乘上一個加強因子時不等式取等號條件也不會發生變化.不論是加強余項還是加強因子，它們在加強等腰取等不等式或者使其反向中扮演著重要角色，在等腰取等不等式研究中有著特殊的地位和作用.

等腰取等量對加、減、乘、除運算是封閉的，即任何兩個等腰取等量對加、減、乘、除運算產生的結果仍是等腰取等量.根據這個性質就可以對等腰取等不等式進行加強，并發現新的等腰取等不等式.

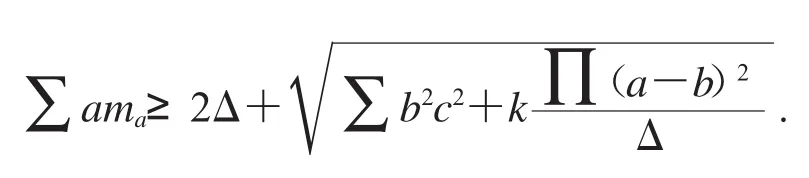
結果發現了反向的等腰取等不等式

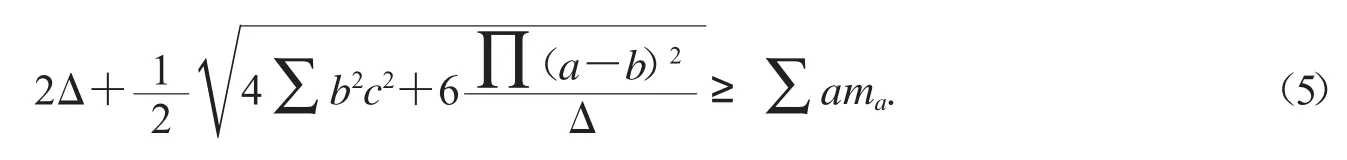
試證明不等式（5）.

由于等腰取等量的這些性質，在對等腰取等不等式進行放縮的過程中始終用等腰取等量，這樣能夠保證所得結果永遠為等腰取等不等式，而不至于退化為普通的三角形幾何不等式.

2 尹華焱模型及其新探索

尹華焱模型首次出現于文獻[6]中，其內容是：設Q是關于ΔABC線元或角元的零次幾何量，且當b＝c時，Qa＝1，Qb＝Qc，則可構造出一個等腰三角形時取等號的不等式

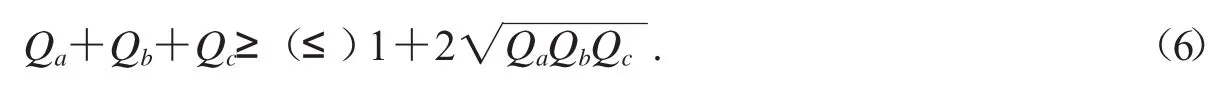
至于（6）式是否成立，要視Q所取表達式的具體情況通過驗證來確定.文獻[6]中模型（6）提出后，尹華焱用其構造了大量等腰三角形時取等號的不等式，楊學枝、褚小光證明了其中的若干不等式，這些結果收入到文獻[6]中.下面介紹筆者研究模型（6）的一些收獲和體會.

從模型（6）的要求來看，只要能夠得到等腰三角形時取等號的局部對稱不等式，就可以得到相應的Q表達式，而等腰三角形時取等號的局部對稱不等式是很多的，這樣就可以得到發現等腰取等不等式的比較實用的途徑.

2.1 模型（6）的內和外

不僅可以通過模型（6）直接構造等腰取等不等式，其它一些看似與（6）式相差甚遠的等腰取等不等式也有可能化為（6）的形式.

例3由模型（6）可驗證發現等腰取等不等式

容易證明不等式（7）等價于不等式（2）和（3），這說明尹華焱模型包含了這兩個有名的不等式.由此可見模型（6）的涵義是相當深刻和廣泛的.

這里出現了一個問題，就是模型（6）的內和外，即可轉化為模型（6）的等腰取等不等式與不可轉化為模型（6）的等腰取等不等式.文獻[8]中筆者提出并證明了若干模型（6）以外的等腰取等不等式.筆者認為，固然利用模型（6）進一步研究等腰取等不等式很有意義，但發現新的模型（6）以外的結果更有價值和意義.

2.2 模型（6）的常規使用

即嚴格地按照模型（6）的條件和要求構造等腰取等不等式.

例4設三角形過Gergonne點的Ceva線為ga，gb，gc，則由模型（6）可發現等腰取等的不等式

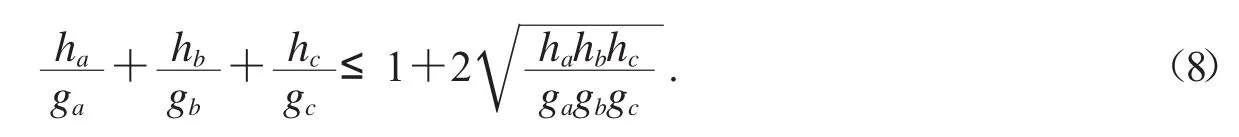
例5由陳計證明的不等式2a2＋bc≥4mbmc（參閱文獻[9]）再結合模型（6），可得等腰取等的不等式

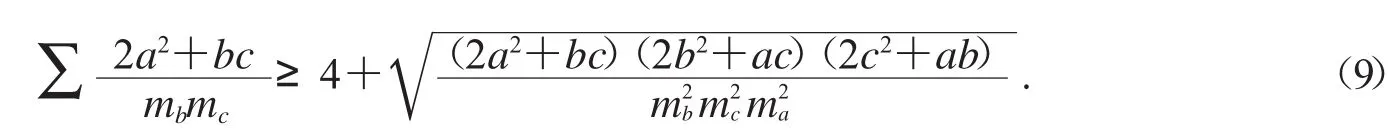
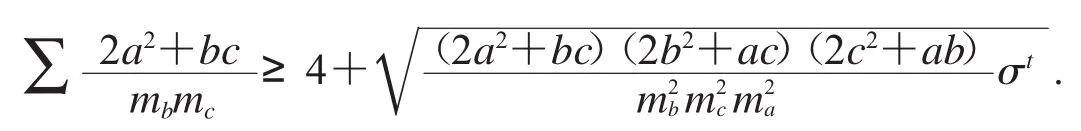
逐次增大指數t的值，驗證所得不等式是否成立.當t＝2時得反向不等式

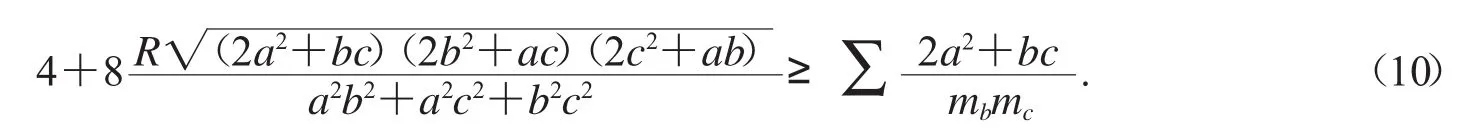
不等式（10）是一個等腰取等的不等式，當然還需要給出證明.

2.3 不等式不成立時可進行調整，使其成立

如果按照模型（6）的要求構造的不等式不成立，此時要進行調整使其成立.注意調整時所用幾何量必須是等腰取等量，否則會改變取等號的條件，我們稱此為“取等號條件的封閉性”.

例6在ΔABC中，熟知有不等式

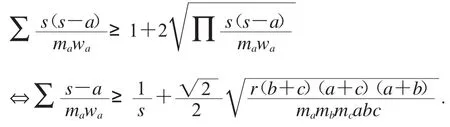
經過驗證知，這個不等式不成立，且反向也不成立.怎么辦？可以應用文獻[10]的調整思想進行調整.事實上，用不等式（2）對上面這個不等式進行放縮（相當于乘了加強因子），可得不等式

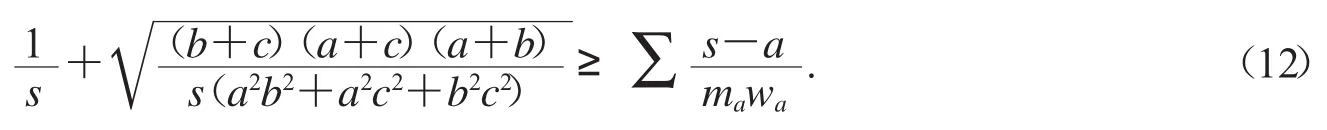
不等式（12）是等腰取等不等式，當然還需要給出證明.

2.4 利用模型（6）發現非等腰取等的普通不等式

設P是關于ΔABC線元或角元的零次幾何量，且當ΔABC為正三角形時P的取值為1（稱這個值為規范值），則模型（6）可變為

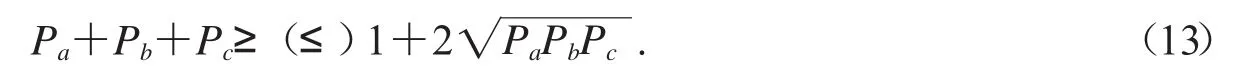
此時不等式（13）不再是等腰取等不等式了，而是一個普通的不等式.

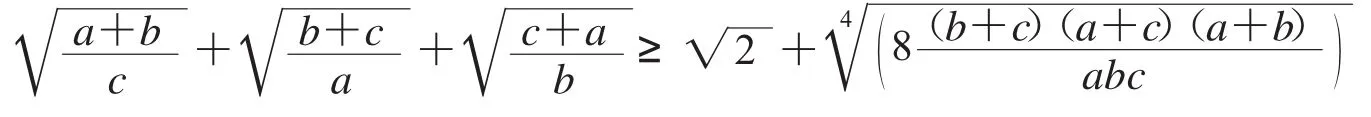
這個不等式成立，且可加強為

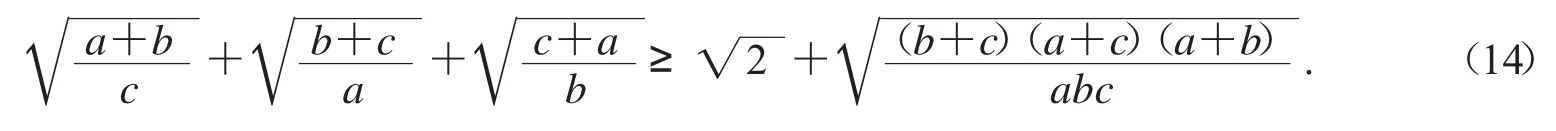
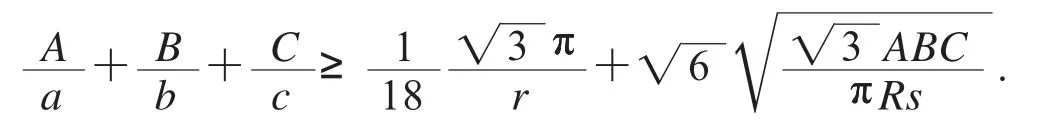
但這個不等式不成立.經過調整得（猜想）

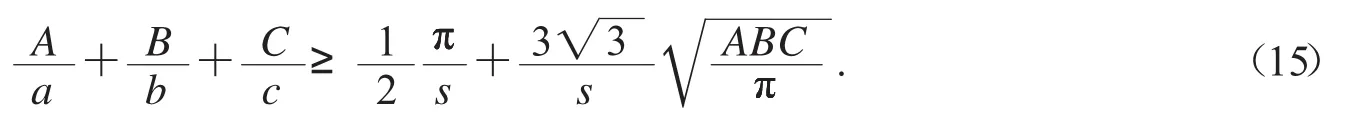
裸角不等式（15）十分優美.

2.5 向多元不等式進行推廣

模型（6）還可向多元不等式進行推廣.設Q是一個四元表達式，且Q的規范值為1，則可構造出不等式

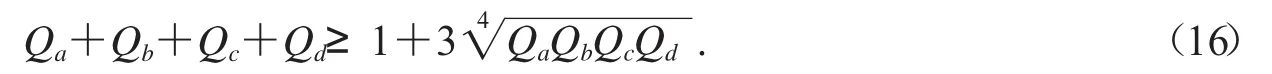
不等式（16）是否成立要進行驗證，如果不成立，可以調整使其成立.

例 9 設 x1，x2，x3，x4＞0，規范值為1，故由（16）可得待驗不等式

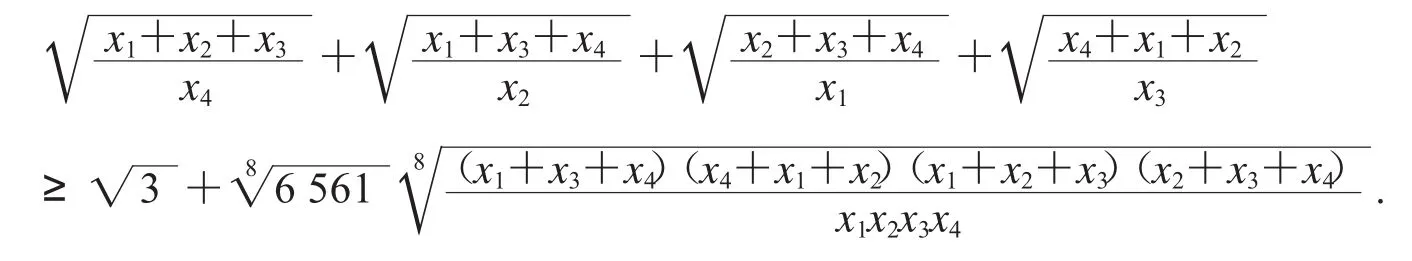
這個不等式成立，且可加強為

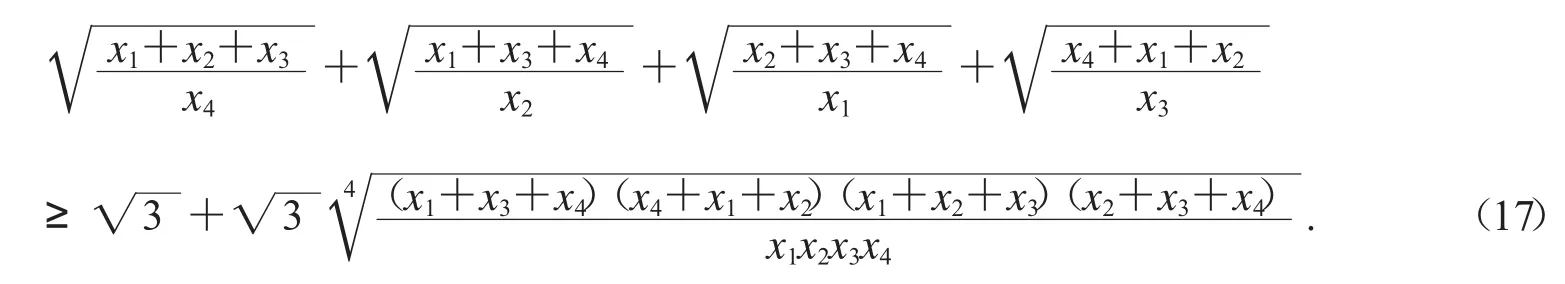
模型（6）還可向四面體進行推廣，限于篇幅，這里不進一步討論了.

3 驗證等腰取等不等式最佳系數的一種方法

確定三角形幾何不等式最佳系數時往往需借助于一些軟件，但對不少問題機器解決不了，對于等腰取等不等式遇到的困難則更多.經過探討，筆者得到了一種驗證等腰取等不等式最佳系數的方法，這個方法的步驟是：

b.對剩下的含有待定參數的式子用正三角形的數據驗證求值，即把三角形中的元素用下面的集合代換

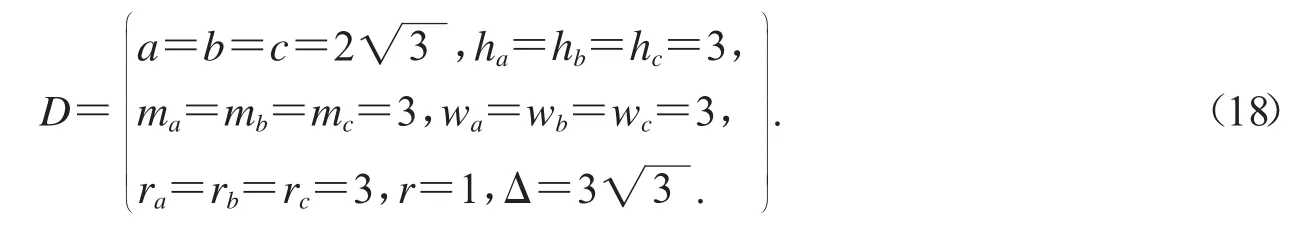
然后令表達式為零，求得參數的值.

c.對所得最佳值進行驗證.

例10在ΔABC中，求最佳k，使不等式

成立.

解 不等式（19）等價于

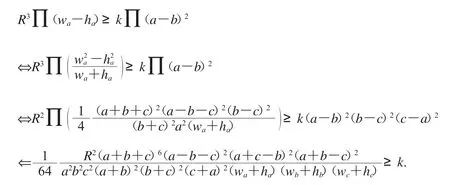
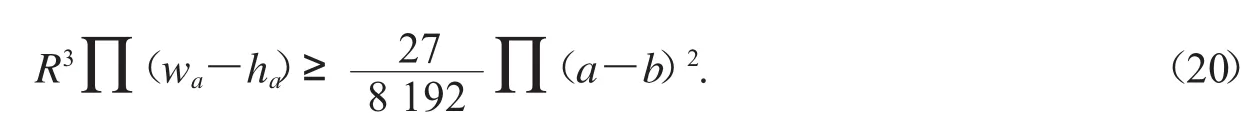
由上述推證知，要證（20）式，只需證

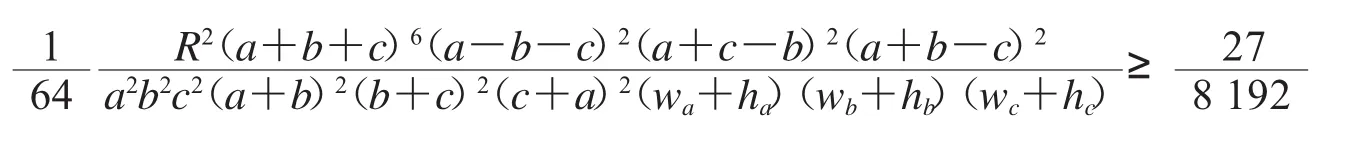
即可，而這容易證明.不等式（20）的反向不等式是

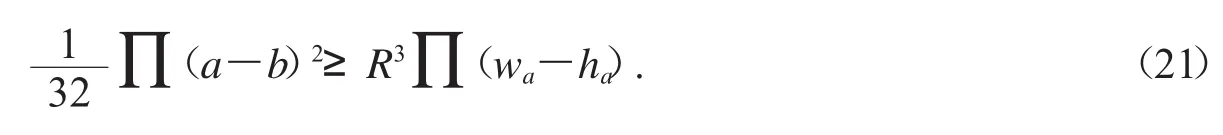
例11在ΔABC中，求最佳k，使不等式

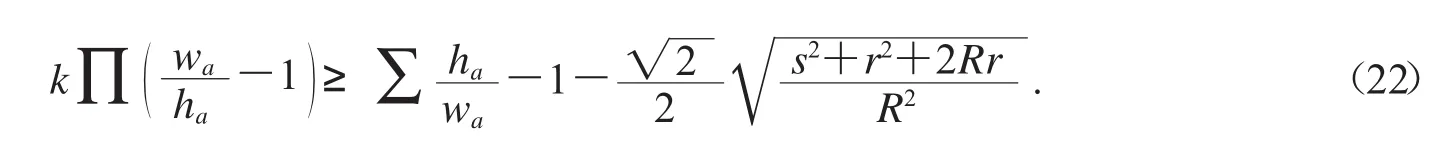
成立.

解 不等式（22）等價于

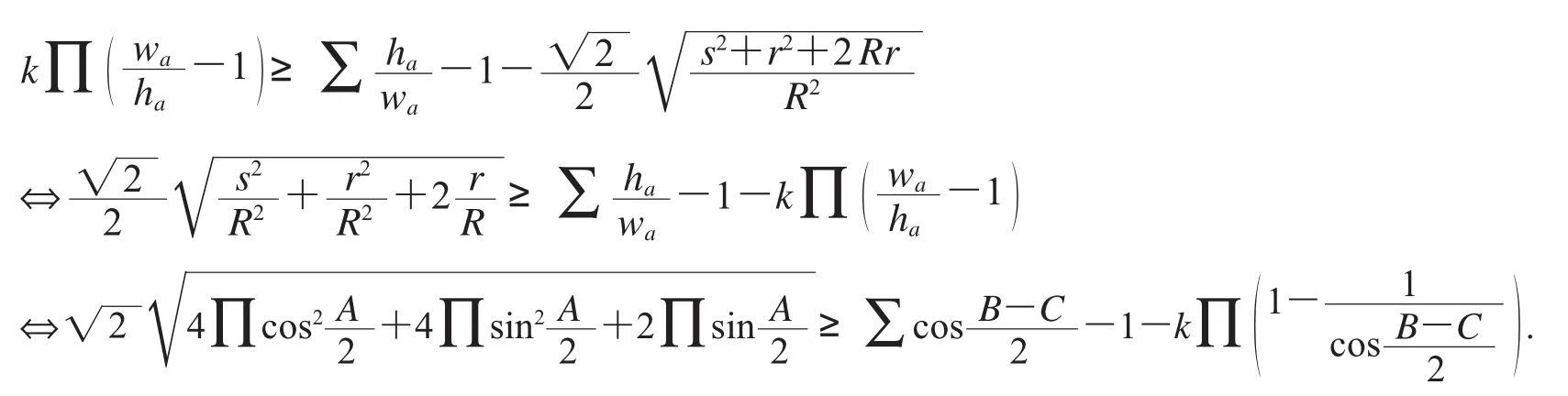
作角代換A→ －2A，B→ －2B，C→ －2C，得銳角三角形中的等價不等式

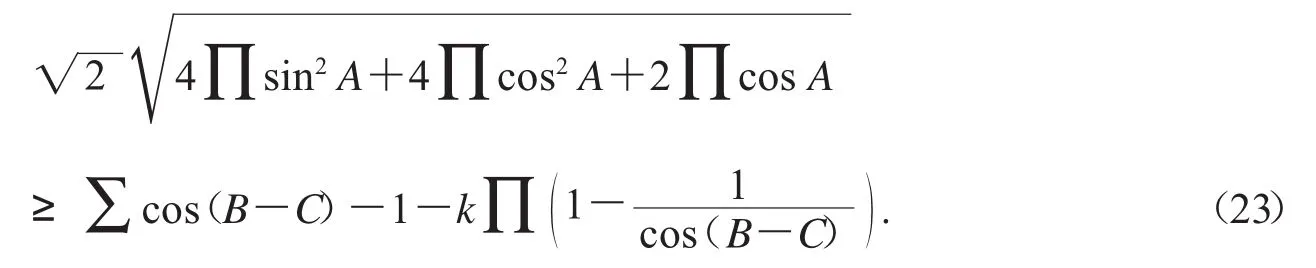
將不等式（23）兩邊同時平方（注意在證明不等式時這一步需要討論），約去因子后，含有參數k的剩余式是

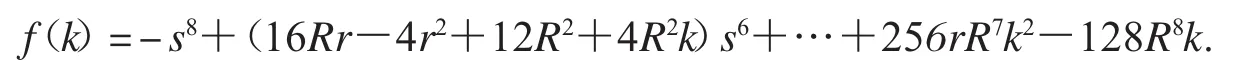
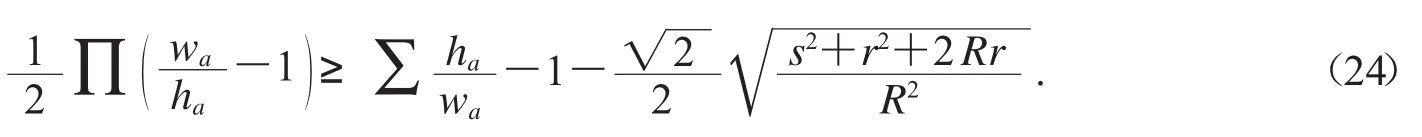
不等式（24）用Bottema軟件[11]驗證成立.注意，為了證明不等式（24），除過證明外，還需要結合一些條件，例如對（23）式兩邊同時平方時討論的情況，這預示著不等式（24）的證明是比較困難的.用類似的方法可以驗證發現不等式上述不等式尤其是不等式（25）和（26），如果用其它軟件或方法來確定不等式的最佳系數是很困難的，甚至是不可能的.

4 與等腰取等不等式不分強弱的不等式

一直以來，從經驗上人們總認為等腰取等不等式是最強的，可以推出其它相應的不等式.但下面這些不等式的出現改變了這個看法，這就是與等腰取等不等式不分強弱的不等式.

例12由排序不等式易證，在ΔABC中，有不等式

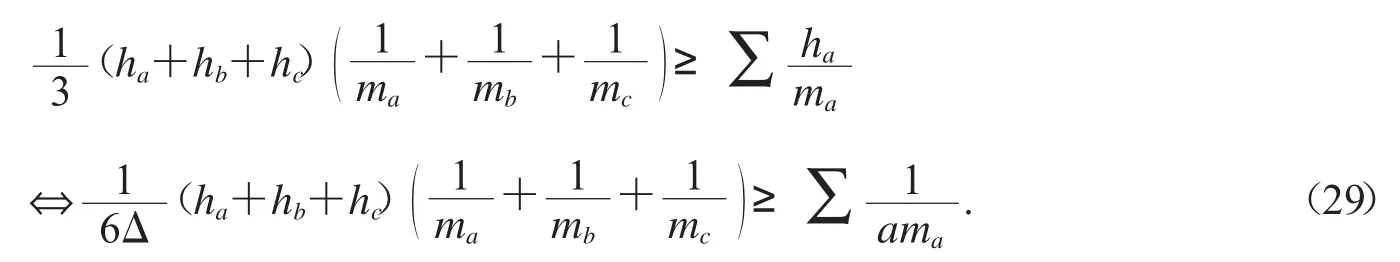
又熟知有等腰取等的不等式（參閱文獻[4]）

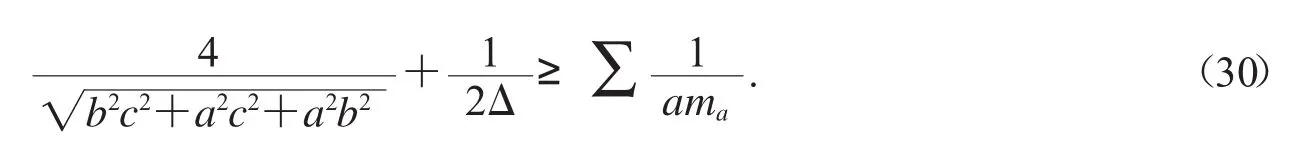
容易驗證不等式（29）與不等式（30）不分強弱.

例13容易證明不等式

不等式（31）不能由等腰取等不等式（4）推出.

5 綜合應用舉例

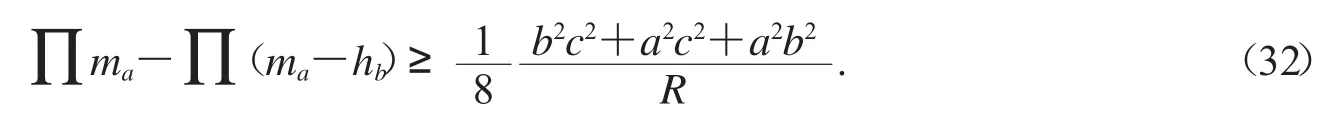
容易證明不等式（32）成立.事實上，如果我們把尹華焱模型寫為

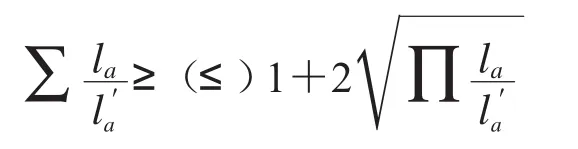
的形式時，可得如下加強模型

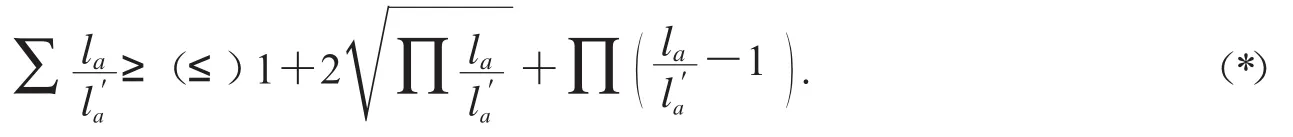
或者

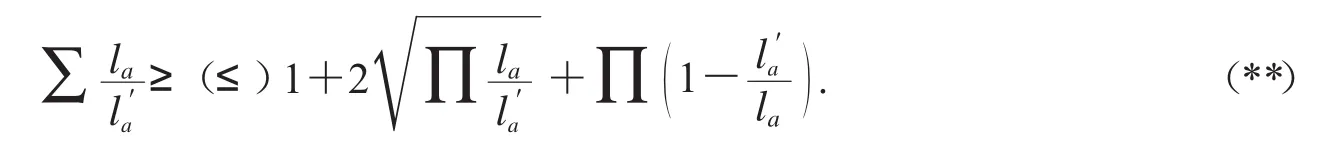
按照這個思路，可得不等式[5]

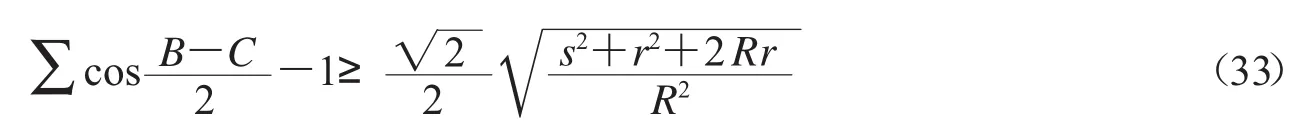
優美的加強式

不等式鏈（34）是等腰取等不等式.也可發現不等式（4）的加強式

例15在ΔABC中，有等腰取等的三角形規范幾何量不等式

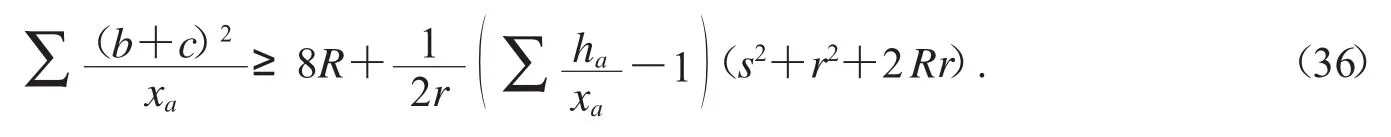
當xa，xb，xc取為中線時，得到的不等式是

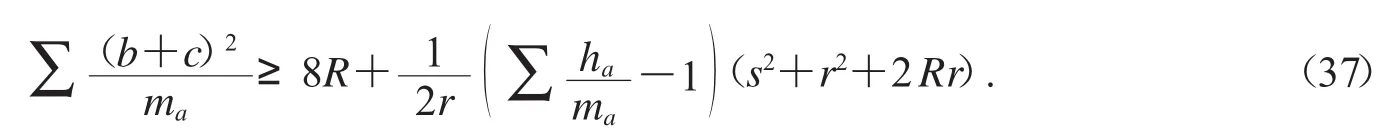
對不等式（37）按照不等式（30）進行調整，得到優美的反向不等式

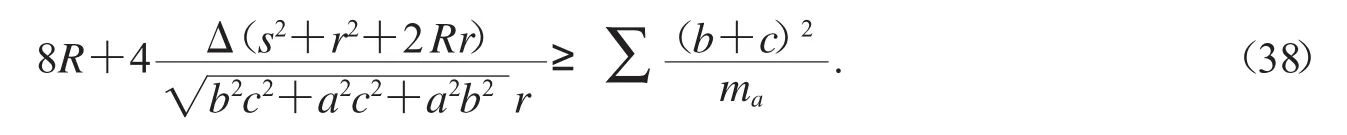
不等式（38）是等腰取等不等式，試證明（38）式.

注意，當（xa，xb，xc）→（ha，hb，hc）時，不等式（36）變為恒等式.當 xa，xb，xc取為角平分線、類似中線等線元時限于篇幅這里不再討論.

例16根據模型（6），寫出待驗式

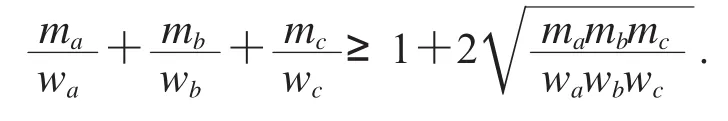
雖然這個待驗式是等腰取等的，但并不成立.不成立沒有關系，我們可以調整使其成立.用（2）式對待驗式進行調整得不等式

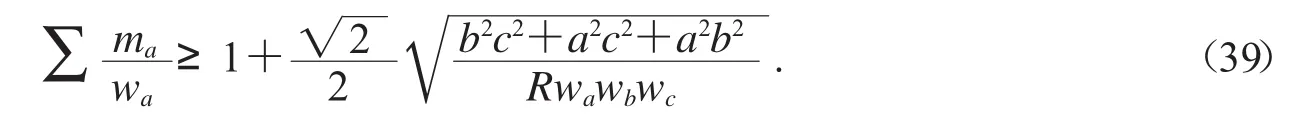
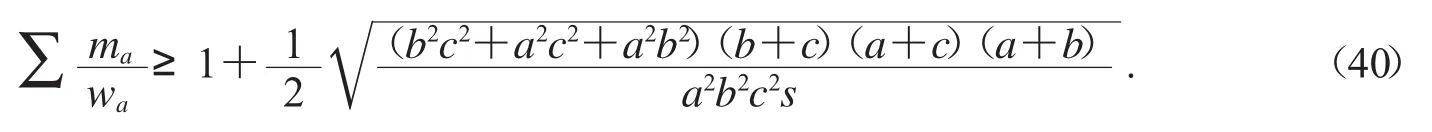
不等式（40）是等腰取等不等式，試證明不等式（40）.同理，用模型（6）可得待驗式

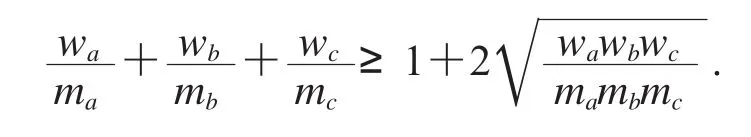
用（2）式調整得

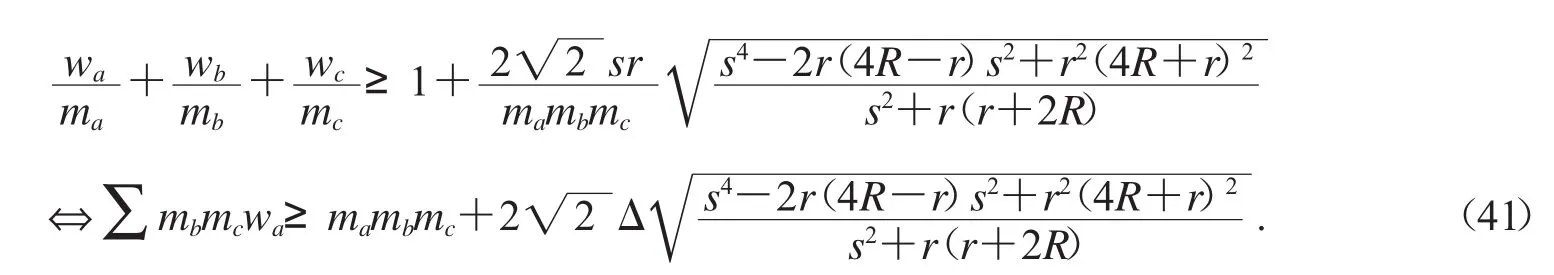
不等式（41）是等腰取等不等式，試證明不等式（41）.