《概率論與數理統計》課程教學方法探究
——以古典概率和條件概率為例

□劉 燕

概率論與數理統計是研究隨機現象的一個數學分支，它是與現實世界聯系緊密、應用最為廣泛的學科之一，已成為人們從事生產勞動、科學研究和社會活動的一個基本工具。其中，古典概率和條件概率是概率論與數理統計課程中兩個基礎且重要的概率，大量的后續概率建立在這兩個概率的基礎之上[1]，比如事件的獨立性、乘法公式、全概率公式和貝葉斯公式、二項分布、隨機向量的條件分布等，因此應重視古典概率和條件概率的教學與學習。文章通過生活案例講述古典概率和條件概率，激發學生的學習興趣，并分析典型的常見錯誤，指出注意問題，避免學生在學習過程中發生不必要的錯誤，增強學生的學習信心，進而提高課堂教學質量與教學效果。

一、古典概率

古典概型定義[2]：設隨機試驗E滿足下列條件：

①(有限性)試驗的樣本空間只有有限個樣本點，即

Ω={ω1,ω2,…,ωn}；

②(等可能性)每個樣本點的發生是等可能的，即

P({ω1})=P({ω2})=…P({ωn}),

則稱隨機試驗E為古典概型。事件A的概率為：

由上可知，計算古典概率首先判斷這個試驗是否為古典概型。確定之后，要弄清樣本空間包含的樣本點總數和隨機事件中的樣本點數，列出比式求出概率。過程看起來并不復雜，但學生往往就在找樣本空間中包含的樣本點總數和隨機事件中所含的樣本點數這兩個數據上遇到困難，原因在于這兩個數據的計算常常涉及到排列和組合、乘法原理和加法原理的知識，結合古典概型的性質，有時還需要建立一個簡單的數學模型[2]。鑒于此，在教學中將抽象的數學問題背景化，從生活實例入手，增強學生的求知欲。下面看幾個生活實例。

例1 試計算福利彩票35選7中特等獎的概率，中一等獎(對6個號碼)的概率？

由上可知，無論中特等獎還是一等獎用古典概率知識可算出它們都是很小的概率事件，在生活實際中很難發生。由此告誡同學們在生活中與其守株待兔等待小概率事件的發生，不如踏實學習、認真工作，慢慢積累財富更為妥當。

例2 某接待站在某一周接待12次來訪，已知這12次接待在周二和周四進行，問是否可判斷接待時間是有規定的？

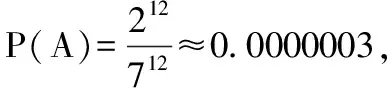
二、條件概率

由此可知，條件概率也可看成古典概率模型，可由古典概率計算，此法稱為縮減樣本空間法。由條件概率定義，當P(B)>0時，P(AB)=P(B)P(A|B)或當P(A)>0時，P(AB)=P(A)P(B|A)，此兩個公式稱為兩事件的乘法公式，它是條件概率的變形，同時也給出了條件概率與乘法公式之間的關系。區別條件概率和積事件的概率關鍵在于是否有附加條件[3]，下面看幾個應用。

例3 設袋中有7只白球，3只紅球。白球中有4只木球，3只塑料球；紅球中有2只木球，1只塑料球。現從袋中任取1球，假設每個球被取到的可能性相同，若已知取到的球是白球，求它是木球的概率？

解析：方法1(公式法)設A表示事件任取一球，取得木球，B表示事件任取一球，取得白球。列表觀察分析

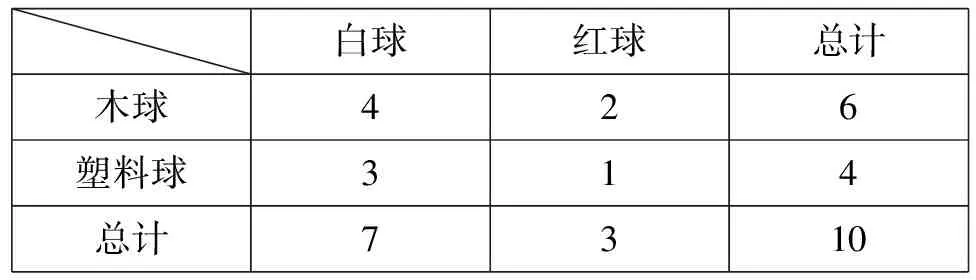
白球紅球總計木球426塑料球314總計7310

AB表示事件取的球是白球且是木球，由上表知事件AB所含的樣本點數為4，事件B所含的樣本點數為7，樣本空間所含的樣本點總數為10，有古典概率可得

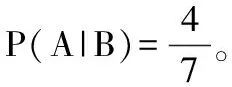
例4 中秋節快到了，想外出游玩兩天，需要知道兩天的天氣情況，已知第一天下雨的概率為0.6，第二天下雨的概率為0.3，兩天都下雨的概率為0.1。想知道(1)第一天下雨時，第二天不下雨的概率;(2)第一天下雨時，第二天也下雨的概率。

解析：設A表示事件第一天下雨，B表示事件第二天下雨，已知P(A)=0.6，P(B)=0.3，P(AB)=0.1。

(1)欲求的概率為A發生條件下事件B不發生的概率，即

由此可知，條件概率與無條件概率之間的大小無確定，即P(B)與P(B|A)的區別在于兩者發生的條件不同，它們是兩個不同的概念，在數值上一般也不相等。

三、古典概率和條件概率常見典型錯誤分析

(一)抽簽模型中的概率與條件概率理解錯誤。

例5 一罐中裝有a個黑球，b個白球，不放回的抽取兩球，已知取出的兩個球中有一個黑球，求另一個球也是黑球的概率。

分析：對于本例，同學們在求解時往往會出現以下錯誤解法。

錯誤解法2：將“兩個球中有一個黑球”理解錯誤。設A1表示兩個球中有一個是黑球事件，A2表示兩個球中另一個是黑球事件，所求概率是在A1發生的條件下事件A2發生的概率，則

此種解法錯誤在于學生將“兩個球中有一個是黑球”理解為“兩球中恰有一個是黑球”導致P(A1)求解錯誤。“兩個球中有一個是黑球”實際指的是“兩球中至少有一個是黑球”。

正確解法：設A1表示兩個球中有一個是黑球事件，A2表示兩個球中另一個是黑球事件，所求概率是在A1發生的條件下事件A2發生的概率，則

(二)積事件的概率與條件概率的理解錯誤。例6一罐中裝有a個黑球，b個白球，不放回的抽取兩球，每次任取一個，求第二次才取到黑球。

錯誤解法：對于這個問題，由于問題中有個“才”字，所以同學們都會注意到“第一次取的球肯定是白球”，但部分學生會犯下如下錯誤：

四、結語

古典概率與條件概率是概率論與數理統計課程中兩個基礎的概率，大量后繼概率在這兩個概率的基礎上引申而來，且它們在實際問題中有著很廣泛的應用。運用實例講解這兩個概率，不僅激發了學生的學習興趣，而且也體現出概率論與數理統計來源于生活，回歸于生活的理念。通過列舉具體實例分析學生在學習這兩個概率過程中出現的典型錯誤，不僅能夠有效地提高教學質量和教學效果，而且對每位初學者學好概率論與數理統計及它在自然科學和社會科學各個領域中的應用具有重要的作用。