雙鋼管管幕結構的抗彎剛度與自重特征分析

馬玉輝 （中鐵二十四局集團安徽工程有限公司，安徽 合肥 230000）

1 引言

管幕預筑法是在擬建地下工程設定的輪廓位置頂進密排大直徑鋼管群，鋼管頂進就位后在鋼管內部澆筑混凝土，后續再在鋼管群保護下開挖、施工內部結構，最終形成地下空間的一種建造方法。管幕預筑法常用于穿越道路、鐵路、結構物、機場等工程的非開挖技術，具有對地面交通影響小、地表沉降小、對復雜環境適應性強等特點[1-4]。

大直徑鋼管內部填充混凝土，故管幕結構的剛度由鋼管與混凝土共同組成，剛度越大其變形越小。劉增龍[5]以北京首都國際機場2號航站樓與3號航站樓之間的聯絡通道穿越機場跑道工程為背景，對大跨度淺覆土管幕暗挖法施工引起機場跑道沉降變形規律進行了分析，結果表明最大沉降點發生在中心軸位置，達到-13mm。陶連金等[6]依托實際工程對管幕施工及新建地鐵隧道下穿既有地鐵隧道施工過程進行了數值分析，結果表明在管幕預支護體系作用下，新建隧道的施工對上部地層的擾動以沉降為主；新建地鐵左、右線隧道施工引起的土層沉降具有疊加效應。張超哲等[7-8]探討了一種采用H型鋼連接的新型管幕結構的受力特征和破壞規律，結果表明鋼管壁厚對承載力影響明顯，翼緣板厚度對其影響不明顯，混凝土強度對其具有一定影響。趙文等[9]對一種采用翼緣板—槽鋼連接的新型管幕結構抗彎性能的關鍵參數進行了分析，結果表明鋼管壁厚和混凝土強度的增加對構件承載力具有一定的影響。韓現民等[10]對以下穿太原火車站工程為依托，對鋼管與混凝土間界面狀態、構件截面幾何特征和管壁厚度等對結構構件抗彎能力影響進行研究。結果表明截面幾何特征對承載能力影響較大，截面極限抗彎承載力隨管壁厚度的減小而呈線性減小規律。另外還有其他學者[11-14]對管幕的受力與變形性能進行了廣泛研究，為深入了解管幕的變形機制提供了重要理論基礎。

但目前大多數研究僅關注鋼管直徑、壁厚增加對鋼管剛度的有利影響，而較少涉及管幕總體重量增加對沉降變形的不利影響。事實上，一方面鋼管直徑越大其抗彎剛度越大，但另一方面其總重量也越大[15，16]。在箱涵頂進就位的最危險工況中，若管幕結構橫向剛度較小，管幕的大部分重量往往由兩端的管幕梁承擔，對于大跨度管幕結構來說，管幕梁承擔了過大的上覆荷載，可能導致變形過大。

可見，有必要發展一種剛度較大而總體重量相對較小的管幕結構，以保證大跨度管幕結構的變形在允許范圍內。現以合肥市濱湖科學城大連路(青海路—包河大道)道路及綜合管廊工程為依托，探討鋼管剛度及自重變化對下穿機場主跑道管幕結構的變形影響。

2 傳統管幕結構抗彎剛度特征

2.1 工程概況

合肥市濱湖科學城大連路位于中央公園內，東西走向，西起青海路，東至包河大道，道路全長約2.3km，規劃為城市主干路，雙向六車道，設計時速60km/h。大連路隧道設計范圍西起青海路，下穿現狀駱崗機場跑道，止于新建廬州大道交點，為保留公園內機場跑道，采用管幕法隧道頂進施工，暗埋段隧道全長495m，敞口段U型槽長度235m。

合肥市大連路隧道工程在樁號4+87.45～6+81.15處下穿合肥市駱崗機場跑道（跑道已棄用），平面交角69°，地下道路與綜合管廊結構樁間水平最小凈距4.87m，頂部覆土5.3～6.13m。該節點采用預制隧道頂進法施工，頂進長度約93.7m。管幕支護設計方案采用44根壁厚16mm直徑1.6m長的帶鎖扣定制鋼管組成四周口字型結構，鎖扣分為雌扣和雄扣，鎖扣采用工廠焊接熱軋不等邊角鋼，頂進長度為92.7m，斷面如圖1所示。鋼管頂進采用2臺直徑1.6m泥水平衡頂管機由東工作井往西接收井掘進施工，鋼管單節長不小于6m，分節間采用鴛鴦坡口焊連接，如圖2所示。

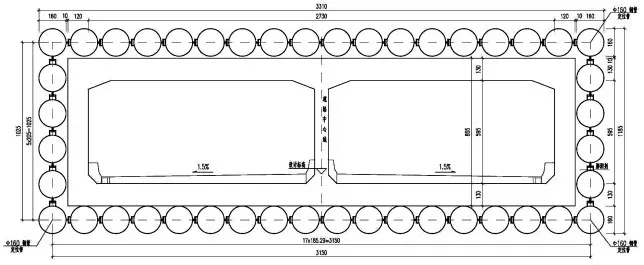
圖1 管幕結構橫斷面圖

圖2 鋼管頂進施工現場圖

鋼管頂進主要位于④1層、④2層中。④1層粘土（Q3al+p）l：層厚1.5～7.8m，層底標高13.50～20.51m，黃褐、褐黃、灰黃色，硬塑狀態，濕，含鐵錳結核、氧化物、高嶺土等，光滑，無搖震反應，干強度及韌性高等，為合肥地區較典型的膨脹土層。④2層粘土（Q3al+p）l：該層土部分鉆孔鉆穿，最大揭示厚度18.8m，褐黃、灰黃、黃褐色，硬塑狀態為主，局部堅硬狀態，濕，含鐵錳質結核（局部富集）、氧化物、高嶺土等，局部間夾薄層粉質粘土，光滑，無搖振反應，干強度及韌性中～高等。

2.2 鋼管抗彎剛度分析

管幕結構中的鋼管橫斷面如圖3所示，鋼管內部被混凝土填充。根據《鋼管混凝土結構技術規范》，鋼管混凝土的截面組合抗彎剛度EI可由式(1)計算[17]。

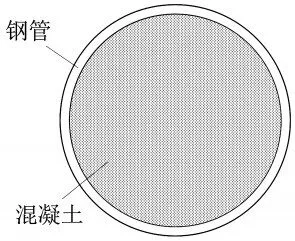
圖3 傳統管幕鋼管橫剖面圖

式中：EI——鋼管混凝土的組合抗彎剛度；Es、Ec——分別為鋼管、鋼管內混凝土的彈性模量；Is、Ic——分別為鋼管、鋼管內混凝土的截面慣性矩。

以鋼管內部填充C20等級混凝土為例，可計算得到不同鋼管直徑時鋼管混凝土的組合抗彎剛度，如圖4所示。可見，管幕鋼管混凝土中，混凝土的抗彎剛度EcIc大于鋼管的抗彎剛度EsIs，且隨著鋼管半徑的增加相互差距越來越大。如鋼管半徑取0.80m時，混凝土抗彎剛度EcIc是鋼管抗彎剛度EsIs的1.47倍。

合肥市大連路隧道工程的鋼管長度為93.7m，現以該長度測算單根鋼管混凝土的自重情況，如圖5所示。可見，管幕鋼管混凝土中，混凝土的自重Gc遠大于鋼管的自重Gs，且隨著鋼管半徑的增加相互差距越來越大。如鋼管半徑取0.80m時，混凝土自重Gc是鋼管自重Gs的7.12倍。

對比圖4與圖5可知，管幕鋼管混凝土中，混凝土一方面提供了較大的抗彎剛度（有利的方面），但另一方面也大大增加了管幕結構的整體自重（不利的方面）。為了考察混凝土的綜合效應，不妨建立一個抗彎剛度與重度比例系數β，其由式(2)確定。β越大，說明相同自重情況下結構具有更大的抗彎剛度，其變形更小，對工程有利。

比例系數β與鋼管半徑的相互關系如圖6所示，可見，鋼管的比例系數βs遠大于混凝土比例系數βc，鋼管混凝土的綜合系數β遠小于鋼管比例系數βs。如鋼管半徑取0.80m時，鋼管比例系數βs是混凝土比例系數βc的4.84倍，管比例系數βs是綜合系數β的3.28倍。

根據上述特征可知，可通過增加鋼管用量、減少混凝土用量，達到提高鋼管混凝土的總體剛度且降低其自重的目的，進而對提高管幕結構穩定性、降低土體變形有利。

3 雙鋼管管幕結構特征分析

3.1 雙鋼管管幕結構設計

為此，本文提出一種高強度雙鋼管管幕結構，其包括外部鋼管、內部鋼管與固定環；固定環由外鋼環、內鋼環與扇形鋼板焊接而成；組裝時，多個固定環基于內鋼環均勻套在內部鋼管外表，再整體嵌于外部鋼管的內部；在外部鋼管與內部鋼管之間澆筑混凝土(或在內部鋼管內部也澆筑混凝土)，由此形成雙鋼管管幕結構。

如果僅在外部鋼管與內部鋼管之間澆筑混凝土，內部鋼管中空，則形成雙鋼管空心管幕結構，如圖7(a)所示；如果所有空隙均澆筑混凝土，則形成雙鋼管實心管幕結構，如圖7(b)所示。可根據實際情況確定是否需要對內部鋼管內側填充混凝土。

圖7 雙鋼管管幕結構橫剖面圖

固定環構型如圖8所示。固定環的內鋼環內徑略大于內部鋼管的外徑、外鋼環外徑略小于外部鋼管的內徑，使固定環能套在內部鋼管外表，如圖9所示。固定環上所有扇形鋼板的弧度總和不大于180°，使后續在外部鋼管與內部鋼管之間澆筑混凝土時，混凝土能夠順利穿越、透過固定環而充滿整個空間。

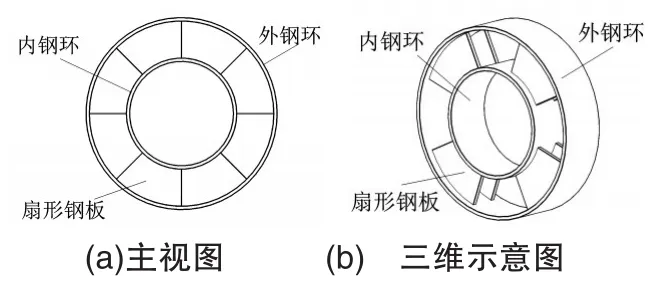
圖8 固定環結構示意圖

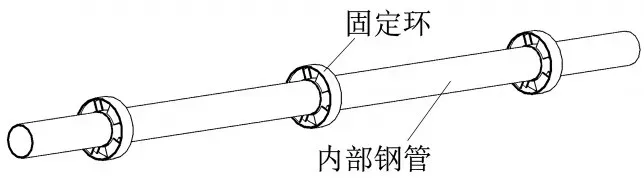
圖9 固定環與內部鋼管連接示意圖

多個固定環均勻、對稱地焊接在內部鋼管的外表，便于內部鋼管基于固定環在外部鋼管內部行走與穿越。外部鋼管、內部鋼管與固定環的相互組裝如圖10所示。

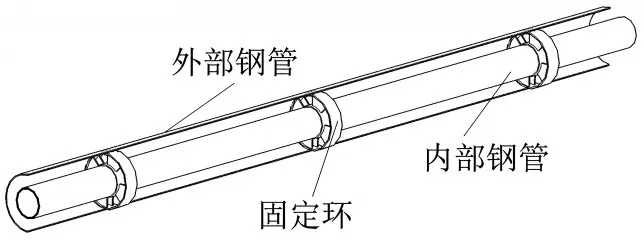
圖10 外部鋼管與內部鋼管連接示意圖

3.2 雙鋼管空心管幕結構剛度特征

根據《鋼管混凝土結構技術規范》[17]，圖7(a)所示空心鋼管混凝土的截面組合抗彎剛度EI可由式(3)計算得到。

式中：I外、I內——分別為外部鋼管、內部鋼管的截面慣性矩，Ic為內外鋼管之間的混凝土截面慣性矩。

以外部鋼管半徑為0.80m為例，計算得到了內部鋼管半徑不同取值時外部鋼管、內部鋼管、內外鋼管之間混凝土及管幕總體的剛度變化情況（內部鋼管中空），如圖11所示。可見：

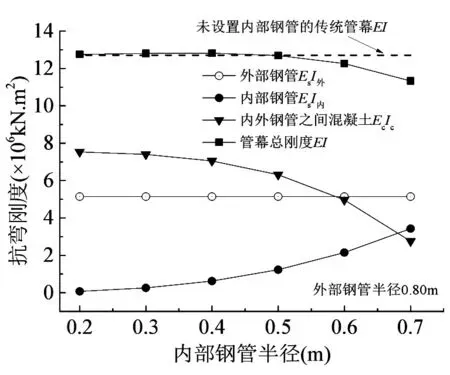
圖11 空心管幕結構抗彎剛度與內部鋼管半徑之間的關系

①隨著內部鋼管半徑的增加，內外鋼管之間混凝土的抗彎剛度逐漸減小，內部鋼管的抗彎剛度逐漸增加，當內部鋼管半徑大于0.60m時，內外鋼管之間混凝土的抗彎剛度開始小于外部鋼管的抗彎剛度；

②當內部鋼管半徑小于0.50m時，內部中空的雙鋼管總體抗彎剛度與未設置內部鋼管的傳統鋼管抗彎剛度基本相等。當內部鋼管半徑大于0.50m時，內部中空的雙鋼管總體抗彎剛度逐漸小于未設置內部鋼管的傳統鋼管抗彎剛度。

進一步得到了內部中空的雙鋼管空心結構的自重分布情況，如圖12所示，可見：

圖12 空心管幕結構自重與內部鋼管半徑的相互關系

①隨著內部鋼管半徑的增加，內外鋼管之間混凝土的自重逐漸減小，內部鋼管的自重逐漸增加，總體上看，內外鋼管之間混凝土的自重遠大于內外鋼管的自重，如內部鋼管半徑為0.50m時，混凝土自重為外部鋼管自重的4.34倍；

②內部中空管幕結構的總自重隨著內部鋼管半徑的增加而減小；

③設置內部中空的內部鋼管后，管幕結構的總自重小于未設置內部鋼管的傳統管幕自重。如內部鋼管半徑為0.50m時，管幕結構的總自重等于未設置內部鋼管的傳統管幕自重的76.1%。

由圖11與圖12可知，當內部鋼管半徑等于0.50m時，雖然雙鋼管空心管幕結構的抗彎剛度與傳統管幕結構的抗彎剛度基本相當，但其自重僅為統管幕結構自重的76.1%，即單根鋼管減少自重達1093kN，顯然對提高管幕結構的穩定性、降低土體變形是有利的。

該方法的技術意義在于：在維持管幕結構抗彎剛度基本不變情況下，通過增設內部鋼管、減少混凝土的澆筑體積，達到了降低管幕結構整體自重的效果，為管幕結構的優化設計提供了新思路。

3.3 雙鋼管實心管幕結構剛度特征

當然，也可以根據需要對內部鋼管也進行混凝土填充，形式雙鋼管實心管幕結構，如圖7(b)所示，現探討該構型的抗彎剛度特征。

以外部鋼管半徑為0.80m為例，計算得到了內部鋼管半徑不同取值時管幕結構的抗彎剛度變化情況，如圖13所示。可見：增設內部鋼管后，隨著內部鋼管半徑的增加，雙鋼管實心管幕結構的抗彎剛度逐漸大于傳統單鋼管實心管幕結構的抗彎剛度。如內部鋼管半徑為0.60m時，雙鋼管實心管幕結構的抗彎剛度比傳統單鋼管實心管幕結構抗彎剛度增大17%。

圖13 雙鋼管實心管幕結構抗彎剛度特征分析

以外部鋼管半徑為0.80m為例，計算得到了內部鋼管半徑不同取值時管幕結構的自重變化情況，如圖14所示。可見：增設內部鋼管后，雙鋼管實心管幕結構的自重略大于傳統單鋼管實心管幕結構的自重。如內部鋼管半徑為0.60m時，雙鋼管實心管幕結構的自重比傳統單鋼管實心管幕結構自重增大9.5%。

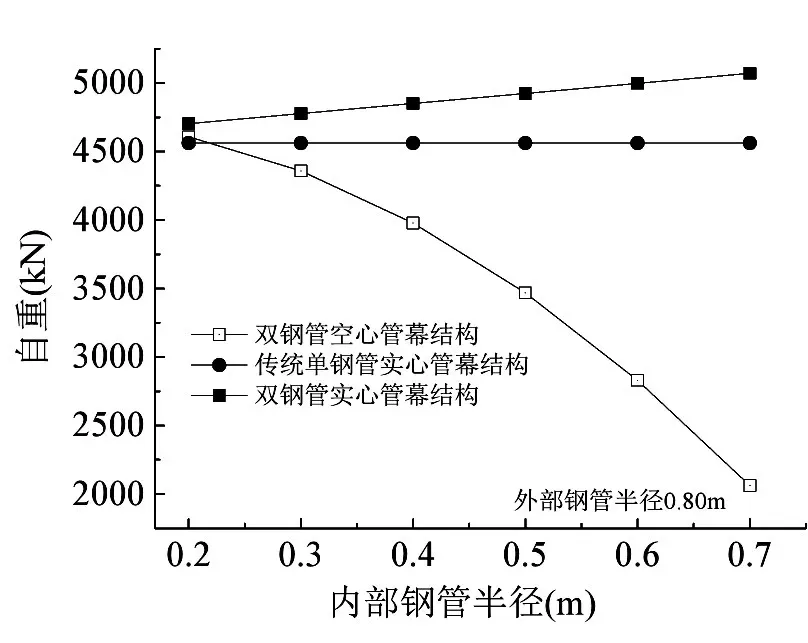
圖14 雙鋼管實心管幕結構自重特征分析

進一步得到了不同工況下管幕結構抗彎剛度與重度比例系數β取值情況，如圖15所示，可見：

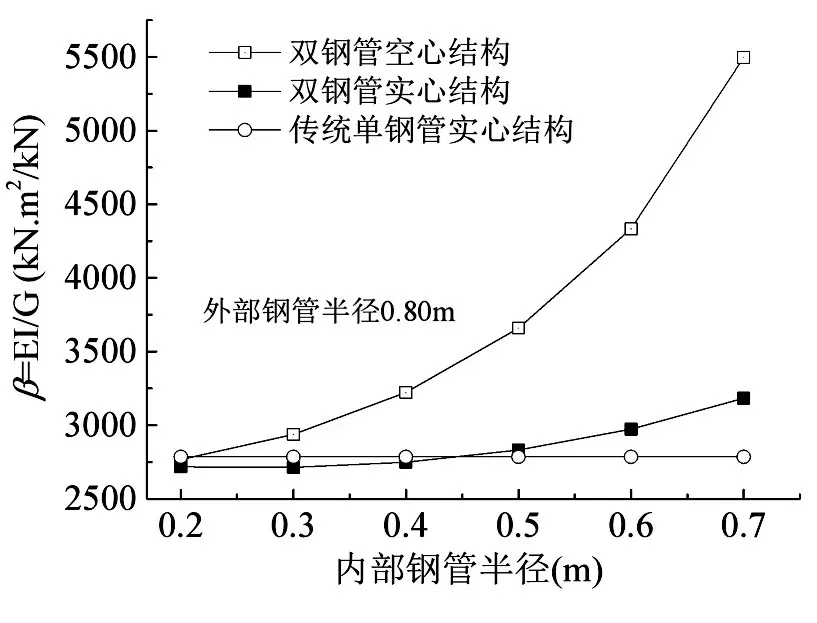
圖15 β與內部鋼管半徑的相互關系

①隨著內部鋼管半徑的增加，雙鋼管空心結構的比例系數逐漸遠大于傳統單鋼管實心結構的比例系數，如內部鋼管半徑為0.60m時，雙鋼管空心管幕結構的抗彎剛度與重度比例系數是傳統單鋼管實心結構相應值的1.56倍，說明雙鋼管空心結構具有較高的“性價比”；

②當內部鋼管半徑小于0.45m時，雙鋼管實心結構的比例系數小于傳統單鋼管實心結構的相應值，但兩者差別不大。

可見，與傳統單鋼管實心管幕結構相比，雙鋼管實心管幕結構的自重略有增加，但其抗彎剛度增加更大，總體上還是有利的。對于管幕結構總體長度不大、管幕自重對整體影響有限的情況下，可以通過增設內部鋼管，可達到提高管幕結構抗彎剛度、降低土體變形的目的。

4 雙鋼管管幕結構的應用

增設內部鋼管后，其造價與傳統管幕結構有所提高，故所提雙鋼管管幕結構可僅在變形較大的關鍵部位使用，而無需在所有位置使用。該做法大大降低了關鍵部位的變形，提高了管幕結構的安全性，而對總體造價影響有限，性價比較高。具體分析如下：

①對于管幕結構整體長度大、上覆土體強度較低、管幕橫向連接剛度較弱、管幕自重對結構變形影響相對較大時，可采用雙鋼管空心結構，其可實現維持管幕結構抗彎剛度基本不變情況下，大大降低管幕結構整體自重的效果。且往往在頂排中部的鋼管變形較大，故僅在頂排中部的局部范圍使用雙鋼管空心結構，其余位置仍采用傳統的單鋼管實心結構，如圖16所示；

圖16 雙鋼管空心管幕結構的應用示意圖

②對于管幕結構整體長度相對不大、管幕橫向連接剛度較好、管幕自重對結構變形影響相對有限時，可采用雙鋼管實心結構，其可實現增大管幕結構抗彎剛度的效果，也僅在頂排中部的局部范圍使用雙鋼管實心結構，其余位置仍采用傳統的單鋼管實心結構，如圖17所示。

圖17 雙鋼管實心管幕結構的應用示意圖

合肥市大連路隧道工程的管幕結構在上述理論的支撐下，對結構進行了一定的優化，確保下穿原駱崗機場跑道的影響在允許范圍內。現場監測數據表明，所提優化是合理可靠的。管幕結構的變形監測規律與機理分析將另文發表。

5 結論

管幕結構中鋼管直徑越大其抗彎剛度越大，但另一方面其總重量也越大，故需綜合考慮鋼管抗彎剛度與自重之間的相互關系，以便得到經濟合理的管幕設計方案。對比分析表明：

①傳統單鋼管實心管幕結構中，混凝土的抗彎剛度大于鋼管的抗彎剛度，且隨著鋼管半徑的增加相互差距越來越大，但同時混凝土的自重遠大于鋼管的自重；

②提出了一種高強度雙鋼管管幕結構，其包括外部鋼管、內部鋼管與固定環，如僅在外部鋼管與內部鋼管之間澆筑混凝土，內部鋼管中空，則形成雙鋼管空心管幕結構，如果所有空隙均澆筑混凝土，則形成雙鋼管實心管幕結構；

③雙鋼管空心管幕結構在維持管幕結構抗彎剛度基本不變情況下，通過增設內部鋼管、減少混凝土的澆筑體積，達到了降低管幕結構整體自重的效果，為管幕結構的優化設計提供了一條新途徑；

④雙鋼管空心管幕結構的抗彎剛度與重度比例系數大于傳統單鋼管實心結構的相應值，說明雙鋼管空心結構具有較高的“性價比”；

⑤與傳統單鋼管實心管幕結構相比，雙鋼管實心管幕結構的自重略有增加，但其抗彎剛度增加更大，總體上還是有利的；

⑥雙鋼管空心管幕結構或雙鋼管實心管幕結構可僅布置在管幕的頂排中部，而其余位置仍采用傳統的單鋼管實心結構，該做法大大降低了關鍵部位的變形，提高了管幕結構的安全性，而對總體造價影響有限，性價比較高。