基于滑模自抗擾的PMLSM 電流偏差解耦控制

趙希梅，吳 岑

（沈陽工業大學 電氣工程學院，遼寧 沈陽 110870）

1 引 言

近年來，隨著日益增長的高速、高精度加工需求，直線電機以其直接驅動的結構和良好的動態性能備受關注［1-2］。永磁直線同步電動機（Permanent Magnet Linear Synchronous Motor，PMLSM）不依靠中間傳動環節，采用直接驅動方式，并且散熱快，在激光加工領域得到了廣泛應用［3-5］。但當電感參數發生變化時，其電流解耦不完全，系統魯棒性不佳。為提高系統魯棒性，必須克服PMLSM 電流耦合以及在運行過程中受到的參數變化的影響。

為消除電機運行過程中參數變化，d、q軸電流間存在的耦合等對系統性能造成的不利影響，學者們采用了各種先進的控制方法。文獻［6］采用內模控制結合自抗擾控制的方法解決了參數敏感問題并抑制外部負載擾動，但在高速運行時會出現振蕩現象。文獻［7］針對d、q軸電流耦合問題，采用電壓前饋解耦的方法通過反饋的d、q軸電流和速度，對兩軸電壓進行補償，并對兩軸電流進行解耦，但解耦效果不明顯。文獻［8］針對d、q軸電流耦合問題，采用電流偏差解耦控制（Current Deviation Decoupling Control，CDDC）的方法進行解耦，但電感參數發生變化時，沒有對該擾動進行相應的補償或抑制，并不能完全實現解耦。文獻［9］利用復矢量電流控制器對d、q軸進行電流解耦，動態性能得到一定改善，但是對外部擾動的魯棒性較差。文獻［10］利用電流差值補償的思想，將定子電流作為狀態變量，設計了電流滑模觀測器得到定子電流估計量，改善了電感參數變化時系統的魯棒性，但控制算法過于復雜。滑模自抗擾控制（Sliding Mode Active Disturbance Rejection Control，SADRC）算 法 能降低系統對參數變化的敏感性，對參數變化所引起的擾動進行觀測并對系統進行補償，系統體現出很強的魯棒性［11］。

為此，本文設計一種基于滑模自抗擾的電流偏差解耦控制（Current Deviation Decoupling Control Based on Sliding Mode Active Disturbance Rejection，SADRC-CDDC）方法來對系統在參數變化時進行電流的解耦，從而提高系統魯棒性。首先，為了解決兩軸電流的耦合問題，分別將兩軸電流的給定與反饋量進行作差比較，經過PI 控制器，從作差處引入兩軸耦合控制項，得到含耦合項的控制方程且計算得到耦合量，與其疊加以補償由電流耦合所引起的偏差，設計了CDDC。然后，對CDDC 的耦合項進行分析，得出由于兩軸電感標稱值與實際不一致，CDDC 不能實現解耦。為實現解耦，建立含有參數變化的d、q軸電流動態方程，選取積分滑模面以及指數趨近律對SADRC 進行設計，用于觀測該擾動，且對系統進行補償，進而實現近似完全解耦。從理論上分析證明了SADRC-CDDC 能保證系統穩定，提高了系統的魯棒性。通過系統實驗，證明了SADRC-CDDC 方案在電流近似完全解耦時明顯提高了系統的魯棒性。

2 PMLSM 數學模型

在d、q旋轉坐標系下PMLSM 的電壓方程為

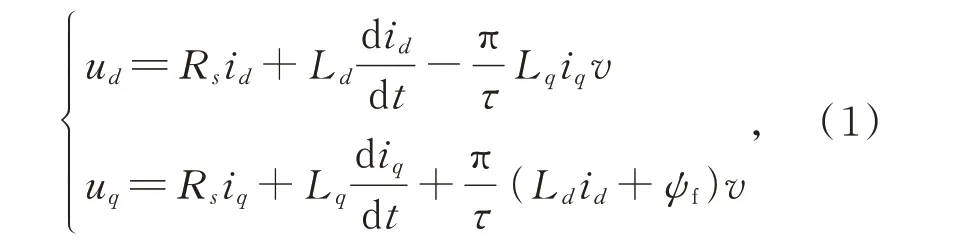
其 中：ud、uq，id、iq和Ld、Lq分 別 為d-q軸 的 電 壓，電流和電感；Rs為定子電阻；ψf為永磁體磁鏈；v為動子速度。考慮參數變化的影響，上式可改為：

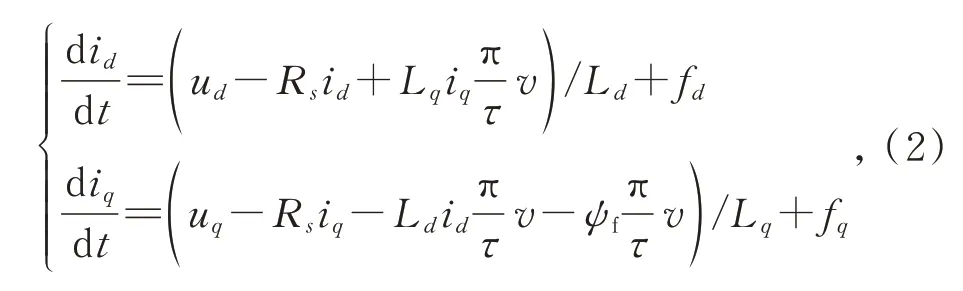
其中：fd、fq分別為d、q軸參數變化的擾動項，定義如下：

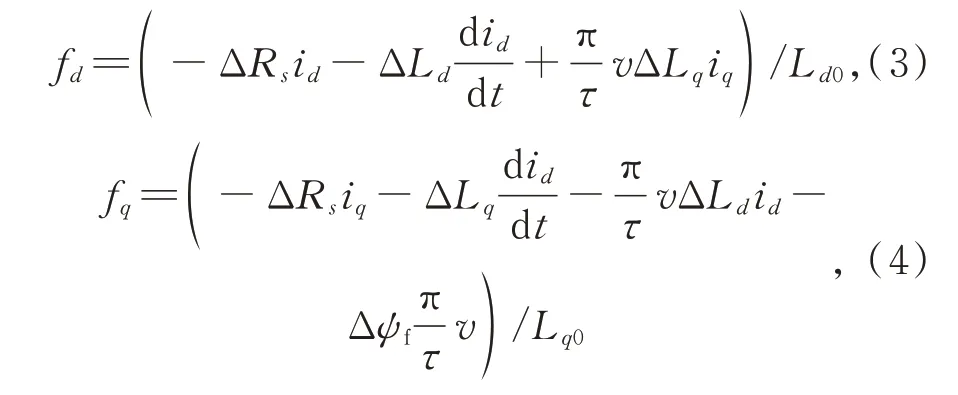
其 中：ΔRs=Rs-Rs0；ΔLd=Ld-Ld0；ΔLq=Lq-Lq0；Δψf=ψf-ψf0；Rs0為定子電阻；Ld0、Lq0分別為d、q軸電感參數的標稱值。 假設|ΔRs|＜a，|ΔLd|＜b，|ΔLq|＜c和|Δψf|＜d；其中：a，b，c和d為參數變化值的上界。

電磁推力方程為：

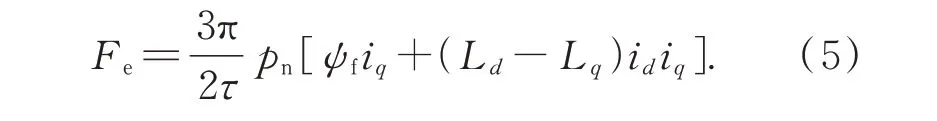
運動方程為：

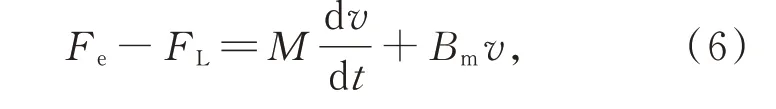
其中，Fe，FL分別為電磁推力和負載擾動；pn為極對數；M為動子質量；Bm為粘滯摩擦系數。

3 PMLSM 控制系統的設計

3.1 PMLSM 系統組成

PMLSM 控制系統結構框圖如圖1 所示。圖中，v*為速度參考輸入。速度控制器的輸入為v*與v的差，控制器采用的是PI 控制器。采用SADRC-CDDC 方法用于電流控制器，經電流檢測以及坐標變換，將d、q軸實際電流與參考電流的差值分別送入SADRC-CDDC。

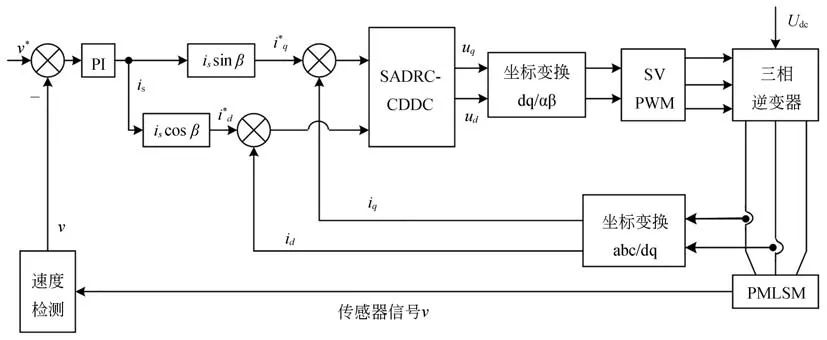
圖1 PMLSM 伺服系統框圖Fig.1 Block diagram of PMLSM servo system

3.2 CDDC 的設計

PMLSM 在正常運行時，電感電流會很大，當其接近飽和，電感值會發生變化；同時，電感值會在運行過程中隨溫度變化而變化。此時，電感實際值與給定值產生偏差，使d-q軸電流存在嚴重耦合。為增強系統在參數變化時的魯棒性，采用CDDC 對d-q軸電流進行解耦。CDDC 框圖如圖2 所示。

圖2 中，G1（s）、G2（s）分別為控制兩軸電流的PI 控制器，G3（s）、G4（s）分別為偏差解耦控制器。分別將兩軸電流的給定與反饋量進行作差比較，經過G1（s）、G2（s），生成各自的給定電壓，再從做差處引入G3（s）、G4（s），與給定電壓加以補償由電流耦合引起的偏差。得到控制方程為：

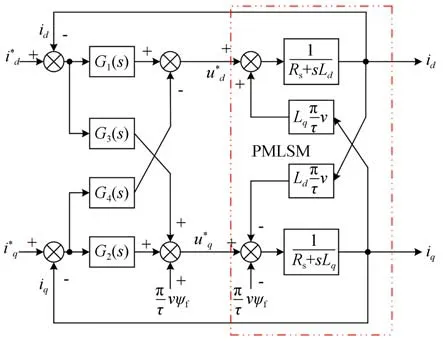
圖2 電流偏差解耦控制框圖Fig.2 Block diagram of current deviation decoupling control

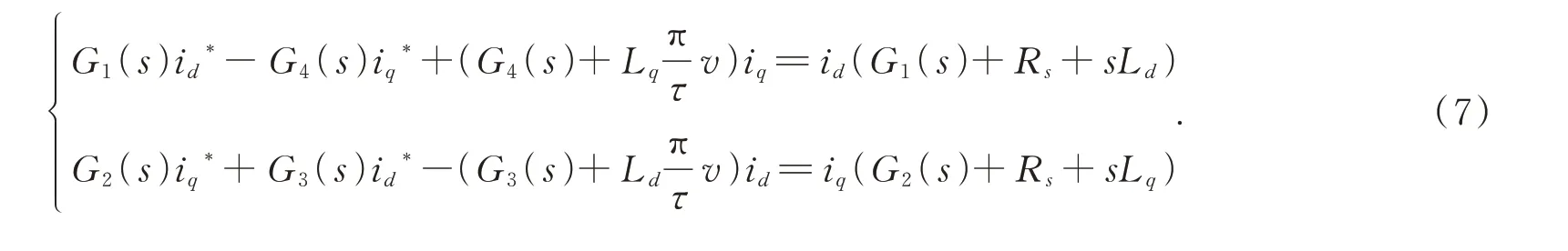
將式（7）進行變換并由克拉姆法則得出兩軸耦合方程為：

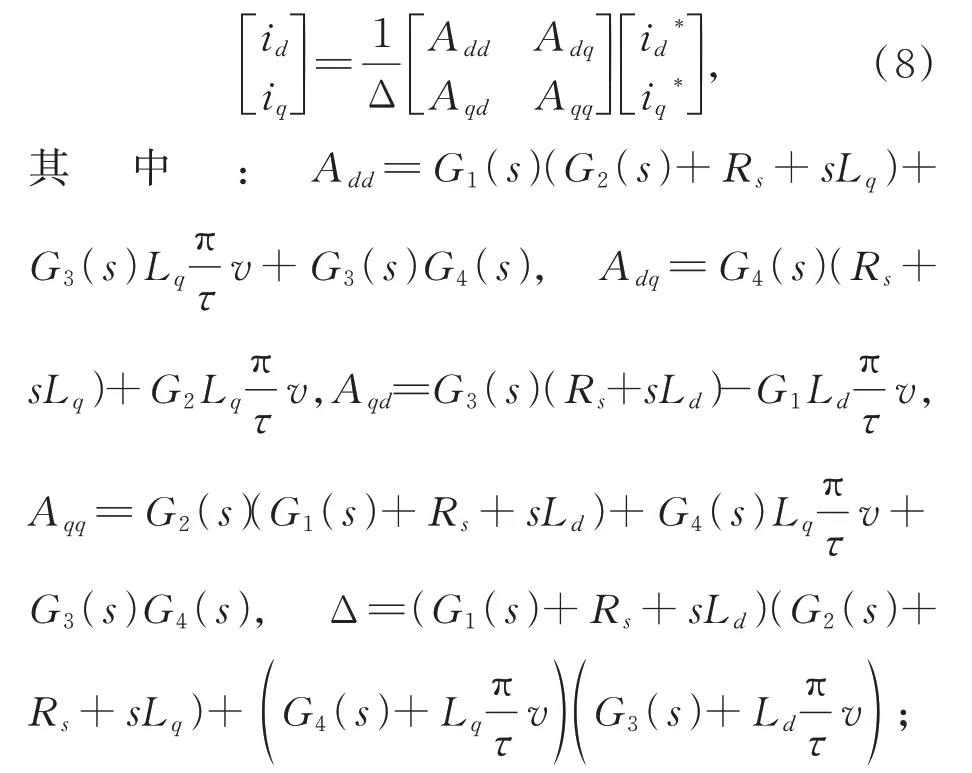
要想實現解耦，要滿足條件Adq/Δ=0、Aqd/Δ=0，由此解得G4（s）、G3（s）為：

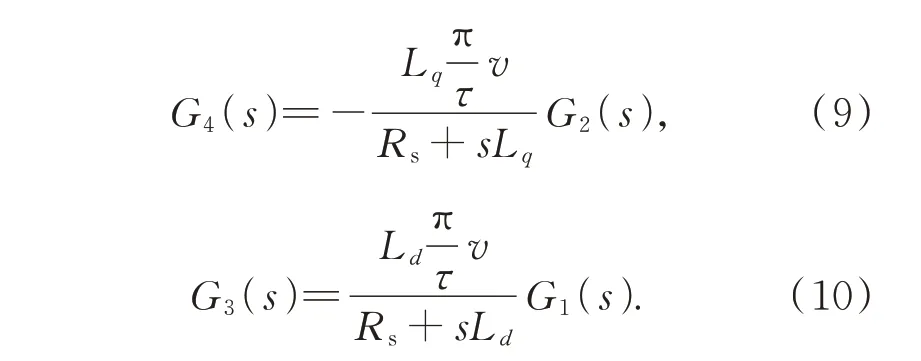
令上式中分子上的Ld、Lq為實際值L^d、L^q，該估計值為電機正常運行時的電感參數。Rs在PMLSM 溫度變化時，阻值變化很小，對解耦控制器G2（s）、G3（s）影響可忽略。由式（9）、（10）知，當且僅當L^d=Ld、L^q=Lq時，才能消除兩軸間電流耦合。

3.3 SADRC-CDDC 的設計

由于參數變化，電感估計值與實際值在運行過程中會產生偏差造成解耦不完全，CDDC 不能完全補償解耦量。為降低系統對參數變化的敏感度，采用SADRC 對參數變化所造成的擾動進行觀測，并對系統進行補償，再解耦。基于SADRC-CDDC 的PMLSM 伺服系統框圖如圖3所示。

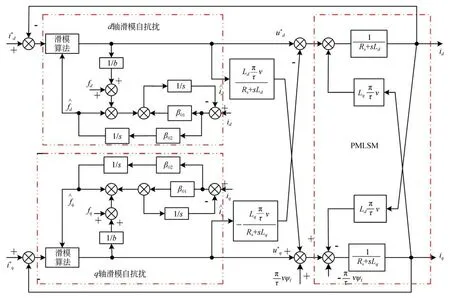
圖3 基于SADRC-CDDC 的PMLSM 伺服系統框圖Fig.3 Block diagram of PMLSM based on SADRC-CDDC

為估計參數變化在q軸所引起的擾動fq，將ADRC 中的觀測器設計為：

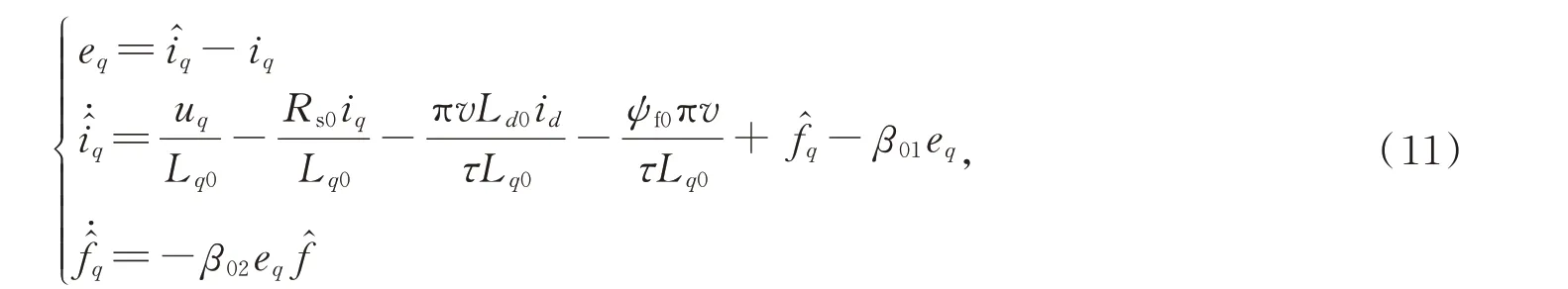
滑模控制算法對擾動具有很強的魯棒性，因此將滑模控制算法引入ADRC，使系統在其參數變化時魯棒性得以保證。

定義q軸電流誤差esq如下：

由式（14）、（15）和（16）有：

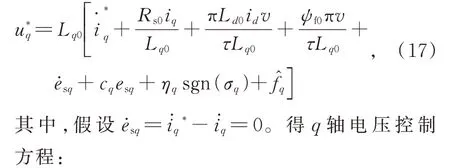
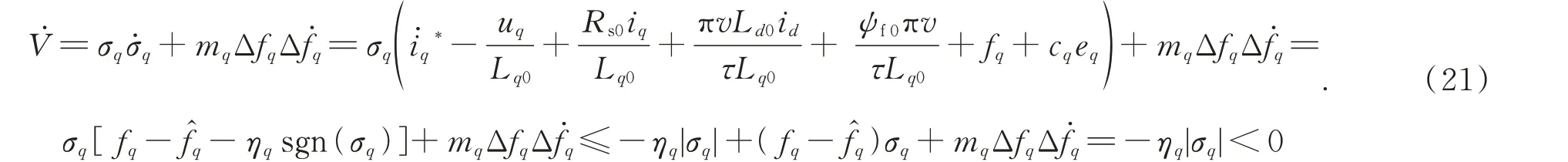
所以V＜0，即證明了q軸電壓控制的漸近穩定性。

同理，d軸電壓的控制方程為：

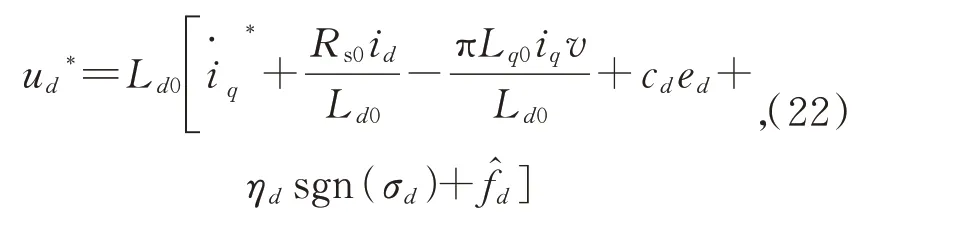
其中：ηd＞0，為d軸擾動估計量。

4 測量實驗與結果

將DSP TMS320F28335 作為PMLSM 伺服系統實驗的核心控制單元，其控制系統結構如圖4 所示。其硬件結構可分為運算控制部分、供電電路單元、檢測元件和PMLSM。運算控制單元為PC 和DSP；PMLSM 的供電部分由整流器和逆變器組成，逆變器開關頻率為5 kHz。測試平臺如圖5 所示。選擇PMLSM 參數為：Ld=0.016 8 H，Lq=0.026 7 H，Rs=2.6 Ω，M=17 kg，Bm=0.2 N·s·m-1，pn=1，ψf=0.24 Wb，電機額定帶載為200 N。為使系統性能最佳，對參數進行反復調試。 PI 參數為Kp=20.6，Ki=179.33；SADRC 參數為ω0=8.75，cd=0.1，ηd=0.5，cq=0.1，ηq=0.3。

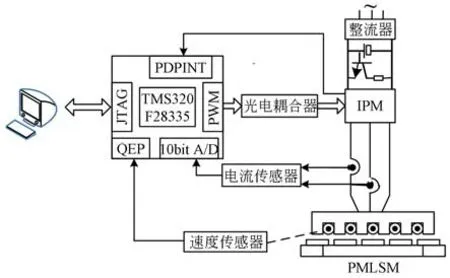
圖4 PMLSM 控制系統硬件結構圖Fig.4 Hardware structure diagram of PMLSM control system

圖5 測試平臺Fig.5 Test platform

圖6 為空載啟動的速度響應曲線。由圖看出，電機在啟動階段，有超調，在0.1 s 達到穩態。電機在0.5 s 突加100 N 負載后，速度減小，經0.04 s 后恢復至給定速度。電機在1 s 時將負載突減至50 N 后，速度增大，經0.01 s 后恢復至給定速度。由此可知，該系統能滿足調速系統要求。

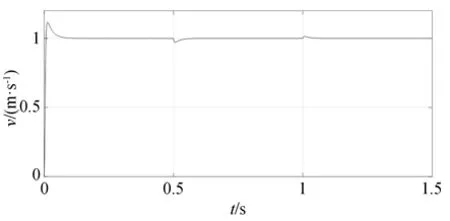
圖6 空載啟動的速度響應曲線Fig.6 Speed response curve of no-load start

圖7（a）和7（b）分 別 為 當Ld=L^d，Lq=L^q時空載啟動在0.5 s 突加100 N 負載和在1s 時將負載突減至50 N，采用CDDC 方法和SADRCCDDC 方法的d、q軸電流的響應曲線。空載時，d軸電流最大振蕩幅度分別為0.37 A 和0.34 A，采用SADRC-CDDC 方法減小了約8.11%，q軸電流最大振蕩幅度分別為0.15 A 和0.13 A，采用SADRC-CDDC 方法減小了約13.33%；在0.5 s 突加100 N 負載后，d軸電流最大振蕩幅度分別為0.51 A 和0.32 A，采用SADRC-CDDC方法減小了約37.25%，q軸電流最大振蕩幅度分別為0.16 A 和0.15 A，采用SADRC-CDDC方法減小了6.25%；在1 s 時將負載突減至50 N后，d軸電流最大振蕩幅度分別為0.32 A 和0.29 A，采用SADRC-CDDC 方法減小了約9.38%，q軸電流最大振蕩幅度分別為0.49 A 和0.47 A，采用SADRC-CDDC 方法減小了約4.08%。

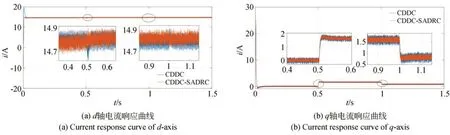
圖7 Ld=，Lq= 時的空載啟動電流響應曲線Fig.7 Current response curves with Ld=，Lq=of no-load start

圖8（a）～8（d）為 當Ld=1.2，Lq=0.8時空載啟動在0.5 s 突加100 N 負載和在1 s 時將負載突減至50 N，采用CDDC 方法和SADRCCDDC 方法的d、q軸電流的響應曲線。空載時，d軸電流最大振蕩幅度分別為0.44 A 和0.20 A，采用SADRC-CDDC 方法減小了約54.55%，q軸電流最大振蕩幅度分別為0.32 A 和0.12 A，采用SADRC-CDDC 方法減小了62.50%；在0.5 s突加100 N 負載后，d軸電流最大振蕩幅度分別為0.42 A 和0.19 A，采用SADRC-CDDC 方法減小了約54.76%，q軸電流最大振蕩幅度分別為0.25 A 和0.11 A，采用SADRC-CDDC 方法減小了56.00%；在1 s 時將負載突減至50 N 后，d軸電流最大振蕩幅度分別為0.43 A 和0.28 A，采用SADRC-CDDC 方法減小了約34.88%，q軸電流最大振蕩幅度分別為0.42 A 和0.12 A，采用SADRC-CDDC 方法減小了約71.43%。當Ld=1.3，Lq=1.5時 空 載 啟 動，在0.5 s 突 加100 N 負載和在1 s 時將負載突減至50 N 時采用采用SADRC-CDDC 方法的電流振蕩幅度明顯減小，魯棒性增強。

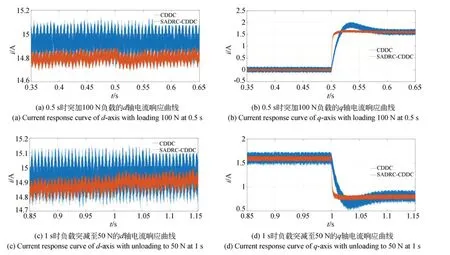
圖8 Ld=1.2，Lq=0.8時的空載啟動d 軸和q 軸電流響應曲線Fig.8 Current response curves of d and q axis with Ld=1.2，Lq=0.8of no-load start

圖9（a）～（d）為當Ld=1.3，Lq=1.5時空載啟動，在0.5 s 時突加100 N 負載和在1 s 時將負載突減至50 N 時采用CDDC 方法和SADRC-CDDC 方法的d、q軸電流的響應曲線。空載時，d軸電流最大振蕩幅度分別為0.45 A 和0.21 A，采用SADRC-CDDC 方法減小了約53.33%，q軸電流最大振蕩幅度為0.31 A 和0.12 A，采用SADRC-CDDC 方法減小了約61.29%；在0.5 s 突 加100 N 負 載 后，d軸 電 流 最大振蕩幅度分別為0.45 A 和0.19 A，采用SADRC-CDDC 方法減小了約57.78%，q軸電流最大振蕩幅度分別為0.25 A 和0.11 A，采用SADRC-CDDC 方法減小了56.00%；在1 s 時將負載突減至50 N 后，d軸電流最大振蕩幅度分別為0.43 A 和0.21 A，采用SADRC-CDDC 方法減小了約51.16%，q軸電流大振蕩幅度分別為0.23 A 和0.12 A，采用SADRC-CDDC 方法減小了約47.83%。 當Ld=1.2，Lq=0.8時 空 載 啟動，在0.5 s 突加100 N 負載和在1 s 時將負載突減至50 N 時采用SADRC-CDDC 方法的電流振蕩幅度明顯減小，魯棒性增強。

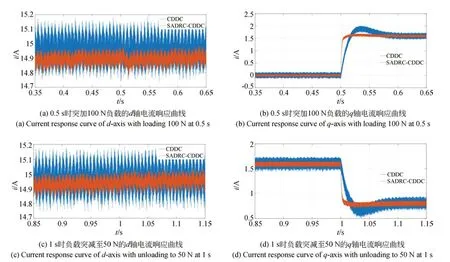
圖9 Ld=1.3，Lq=1.5 時的空載啟動d 軸和q 軸電流響應曲線Fig.9 Current response curves of d and q axis with Ld=1.3，Lq=1.5of no-load start

圖10 為額定負載下啟動的速度響應曲線。由圖看出，電機在啟動階段，有超調，在0.09 s 達到穩態。電機在0.5 s 突減100 N 負載后，速度增大，經0.04 s 后恢復至給定速度。由此可知，該系統能滿足調速系統要求。

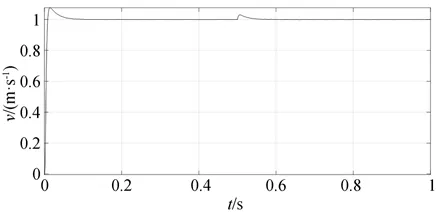
圖10 額定負載啟動的速度響應曲線Fig.10 Speed response curve of rated load start

圖11（a）和（b）分別為當Ld=，Lq=時額定負載下啟動，在0.5 s 突減100 N 負載時采用CDDC 方法和SADRC-CDDC 方法的d、q軸電流的響應曲線。200 N 額定負載時，d軸電流最大振蕩幅度分別為0.21 A 和0.19 A，采用SADRC-CDDC 方法減小了約9.52%，q軸電流最大振蕩幅度為0.31 A 和0.29 A，采用SADRC-CDDC 方法減小了約6.45%；在0.5 s 突減100 N 負載后，d軸電流最大振蕩幅度分別為0.22 A 和0.20 A，采用SADRC-CDDC 方法減小了約9.09%，q軸電流最大振蕩幅度分別為0.32 A 和0.30 A，采 用 SADRC-CDDC 方 法 減 小 了6.25%。

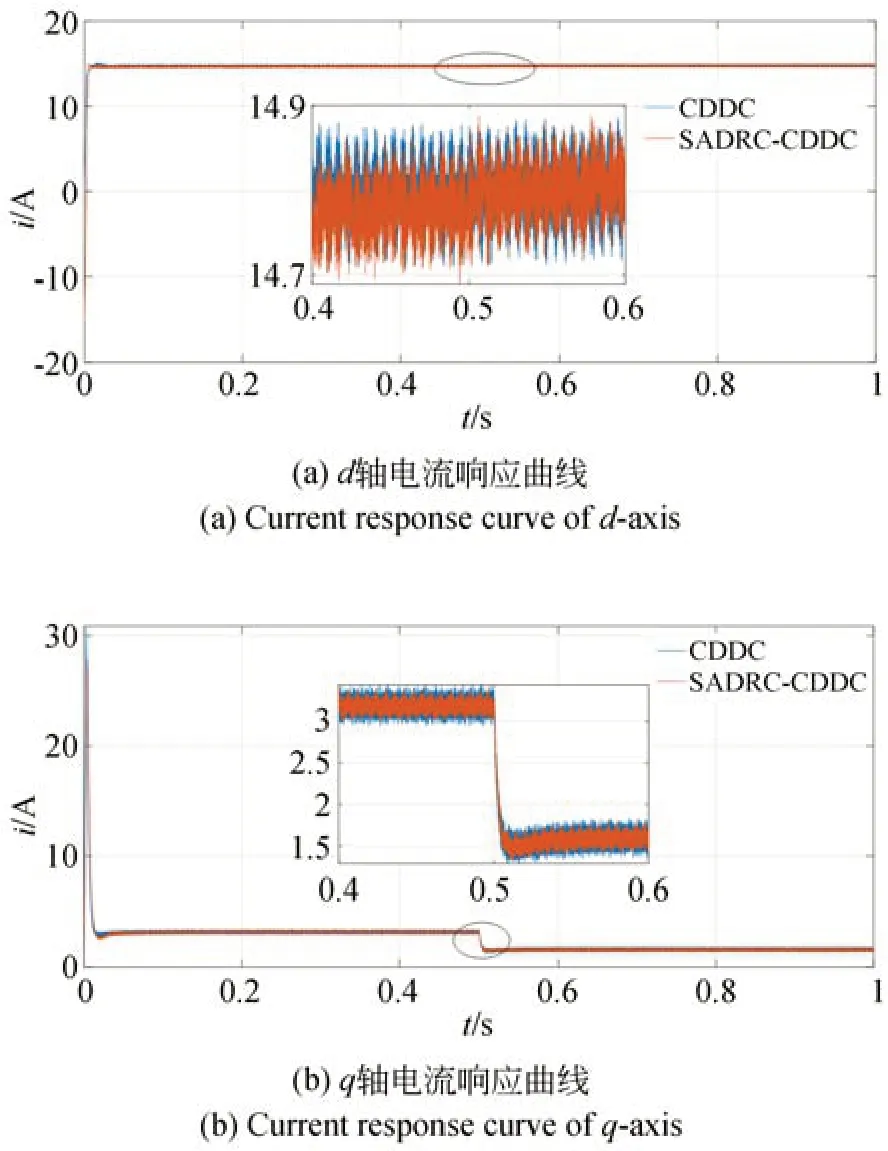
圖11 Ld=，Lq=時額定負載啟動的d 軸和q 軸電流響應曲線Fig.11 Current response curves of d and q axis withLd=，Lq=of rated load start

圖12（a）和（b）分 別 為 當Ld=1.2，Lq=0.8時額定負載下啟動，在0.5 s 突減100 N 負載時采用CDDC 方法和SADRC-CDDC 方法的d、q軸電流的響應曲線。額定負載時，d軸電流最大振蕩幅度分別為0.44 A 和0.22 A，采用SADRC-CDDC 方法減小了50.00%，q軸電流最大振蕩幅度為0.47 A 和0.20 A，采用SADRC-CDDC 方法減小了約57.45%；在0.5 s 突減100 N負載后，d軸電流最大振蕩幅度分別為0.43 A 和0.21 A，采用SADRC-CDDC 方法減小了約51.16%，q軸電流最大振蕩幅度分別為0.45 A和0.23 A，采用SADRC-CDDC 方法減小了約48.89%。當Ld=1.2，Lq=0.8時額定負載下啟動，在0.5 s 突減100 N 負載時采用SADRCCDDC 方法的電流振蕩幅度明顯減小，魯棒性增強。

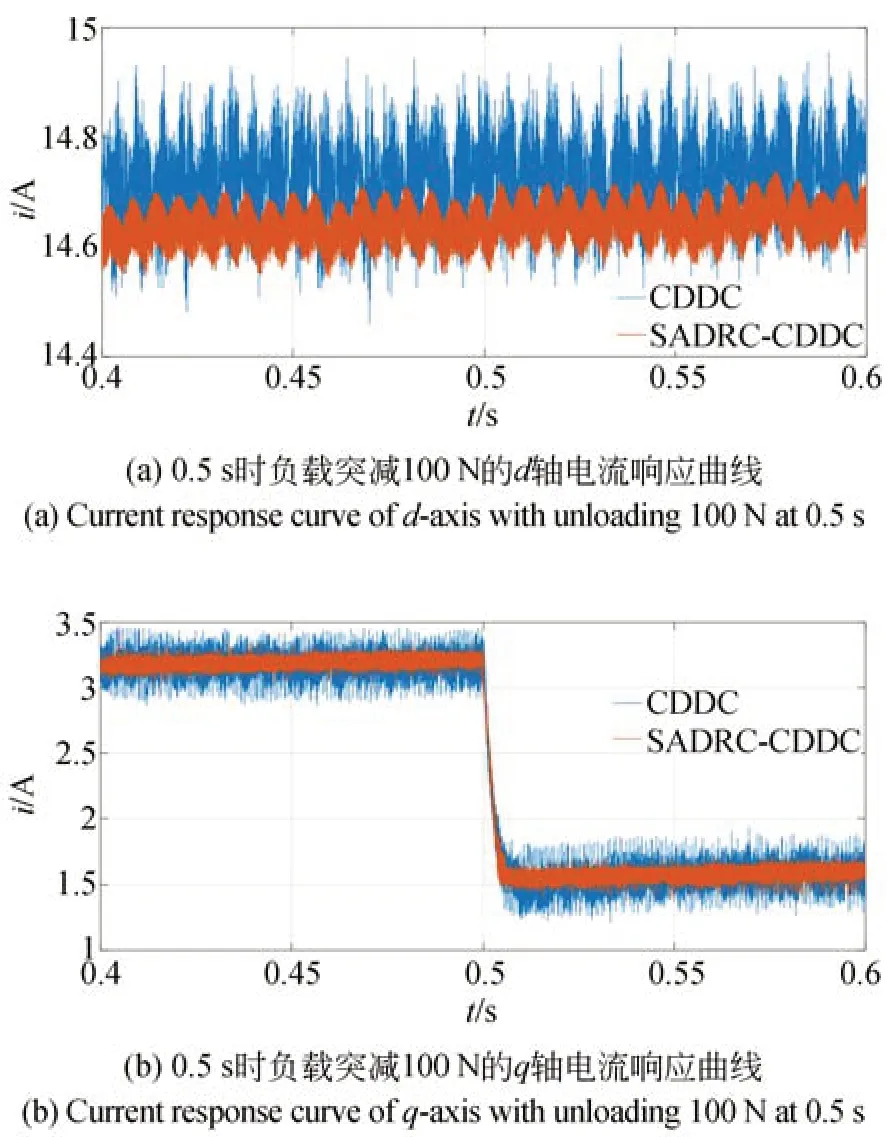
圖12 Ld=1.2，Lq=0.8 時 額 定 負 載 啟 動 的d 軸 和q 軸電流響應曲線Fig.12 Current response curves of d and q axis with Ld=1.2，Lq=0.8of rated load start

圖13（a）和（b）分 別 為 當Ld=1.3，Lq=1.5時額定負載下啟動，在0.5 s 突減100 N 負載時采用CDDC 方法和SADRC-CDDC 方法的d-q軸電流的響應曲線。額定負載時，d軸電流最大振蕩幅度分別為0.42 A 和0.19 A，采用SADRC-CDDC 方法減小了約54.76%，q軸電流最大振蕩幅度為0.49 A 和0.20 A，采用SADRCCDDC 方法減小了約59.18%；在0.5 s 突減100 N 負載后，d軸電流最大振蕩幅度分別為0.44 A和0.21 A，采用SADRC-CDDC 方法減小了約52.27%，q軸電流最大振蕩幅度分別為0.45 A和0.21 A，采用SADRC-CDDC 方法減小了約53.33%。當Ld=1.3，Lq=1.5時額定負載下啟動，在0.5 s 突減100 N 負載時采用SADRCCDDC 方法的電流振蕩幅度明顯減小，魯棒性增強。

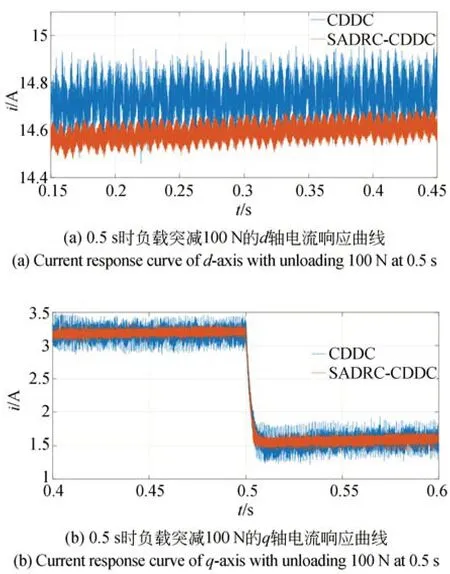
圖13 Ld=1.3，Lq=1.5 時 額 定 負 載 啟 動 的d 軸 和q 軸電流響應曲線Fig.13 Current response curves of d and q axis with Ld=1.3，Lq=1.5 of rated load start

通過以上分析，無論是空載啟動實驗還是額定負載啟動實驗，電感實際值與標稱值相等時（即Ld=，Lq=時）采用CDDC 和SADRCCDDC 方法的電流振蕩幅度無明顯差別；而電感實際值與標稱值不相等時（即Ld=1.2，Lq=0.8和Ld=1.3，Lq=1.5時），采用SADRCCDDC 方法的電流振蕩幅度相對于CDDC 方法明顯減小，降低了參數變化的敏感性，在電感參數變化時實現近似完全解耦，系統表現出很強的魯棒性，而CDDC 方法對電機參數具有很強的依賴性。

5 結 論

針對PMLSM 伺服系統易受電感參數變化影響，且d、q軸電流存在耦合，降低了系統的魯棒性問題。為了對兩軸電流進行解耦，設計了SADRC-CDDC。若只采用CDDC 方法構造耦合多項式，分析得到電感參數變化時不能實現解耦。利用SADRC 對參數造成的擾動進行觀測，再對系統進行補償，在克服參數變化擾動的同時實現對電流的近似完全解耦。通過理論和實驗分析得出，SADRC-CDDC 方法與CDDC 方法比較，在電機運行過程中，系統對參數變化的敏感度降低，由于耦合而造成的d、q軸電流振蕩幅度明顯減少，參數變化情況下d軸電流最大振蕩幅度減少了34.88%～54.76%，q軸電流最大振蕩幅度減少了47.83%～71.43%，系統魯棒性增強，實現了系統的近似完全解耦。