基于二維隨機場的地基大型光學望遠鏡風擾動時程模擬與性能預測

曹玉巖，王建立，王志臣，李洪文，張 巖，初宏亮，李玉霞

（1. 中國科學院 長春光學精密機械與物理研究所，吉林 長春 130033；2. 中國科學院大學，北京 100049）

1 引 言

地基望遠鏡是連接人類與未知宇宙的橋梁，幫助人們觀測、探索宇宙奧秘。隨著對宇宙暗弱目標研究的深入，對如深空恒星的形成與演變、星系分布與結構及演變物理過程對人類的影響、暗物質與暗能量的本質等等的探索，要求未來的望遠鏡不但要看的清、還要看得遠，這推動了地基望遠鏡朝大口徑、高分辨力方向發展［1］。

隨著地基望遠鏡口徑不斷增大，風擾動成為影響望遠鏡成像質量最為關鍵的因素之一。首先，望遠鏡臺址通常選在高海拔偏僻地區來避免雜光污染并提高大氣視寧度，這些地區通常風速都很大（如夏威夷莫納克亞山天文臺風速高達20 m/s）。其次，望遠鏡結構剛度隨口徑的增大而下降，系統諧振頻率隨之降低。此外，風擾動功率譜中包含有較大的低頻能量（0.1～1 Hz），在望遠鏡基頻處風壓能量集中，容易引起望遠鏡系統的共振，而且風載具有隨機和時變特性［2］。一些望遠鏡往往因為風大而難以獲取有效科學數據，甚至不得不放棄觀測。風擾動的分析與抑制已成為地基望遠鏡領域的熱點和難點，受到了越來越多的科學家們的關注［3-10］。

盡管光學望遠鏡外部一般有圓頂防護，能夠顯著降低其內部風速，但為了滿足圓頂內視寧度的要求，內部要適當通風，而且光學望遠鏡波長較短，圓頂內的殘余風仍然會對望遠鏡系統性能產生顯著影響［3］。針對這一問題，MacMynowski等基于Gemini 望遠鏡鏡面風速和風壓測量［5］、風道測試［6］和計算流體動力學仿真CFD［7］得到的數據對望遠鏡圓頂內部的風擾動特性進行了深入研究，并提出了參數化模型［8，9］，該參數化模型可根據望遠鏡、風速及圓頂等相關參數將風擾動轉化為作用在望遠鏡主、次鏡上載荷，給結構設計優化帶來極大的方便。在國內，楊德華等［11］針對LAMOST 反射施密特改正鏡，研究了其拼接子鏡及整體在風擾動作用下的靜態和動態響應，采用風速功率譜密度法分析了其對鏡面面形和跟蹤指向精度的影響；周超等［12］以長春光機所研制的1.23 m 自適應光學望遠鏡為例，研究了風擾動對主鏡面形的影響及望遠鏡在動態風擾作用下的隨機響應；潘年等［13］采用流體動力學仿真方法CFD 研究了國內某2 m 望遠鏡風擾特性，分析了外界風速10 m/s 情況下望遠鏡不同俯仰角時流場中截面空氣速度、壓力、湍流動能以及主鏡面靜壓力的瞬態分布情況，并與Gemini 望遠鏡實測結果進行了比較。徐江海等［14］采用CFD 分析圓頂形式對內部風湍流的影響。以上研究從不同的角度分析了外界風擾動對望遠鏡性能產生的影響。

從上述文獻中可以看出，望遠鏡口徑不斷增大，系統剛度和諧振頻率下降，風擾動的影響應在望遠鏡建造階段予以重視。風擾動包含穩態分量和非穩態分量兩部分，穩態分量（靜態風載荷）是恒定的，通過系統主動控制很容易得到抑制，但抑制非穩態分量（動態風擾動）引起的振動則存在一定的困難。針對此問題，已有多位學者采用計算機仿真手段深入分析了非穩態風擾動對望遠鏡性能的影響程度［8-9］。非穩態風擾動分量具有較強的隨機性，目前已有的大部分研究均是從頻率角度考慮風擾動的影響，時域角度的研究則很少。然而，對于大型地基望遠鏡這樣復雜結構來說，其結構中往往存在一定的非線性特性，風擾動的時程分析模擬是必不可少的，而且從時域角度分析與工作過程更為接近，這也更利于進行實驗比較。

基于上述原因，本文以長春光機所研制的2 m 口徑地基光學望遠鏡為例，從時域角度研究風擾動對望遠鏡的影響，并進行性能預測。首先，詳細介紹了望遠鏡結構組成，基于有限元方法建立結構動力學模型，并通過模態變換方法將動力學模型轉換到模態坐標系下，從而降低了模型維數，提高了計算效率。然后，考慮到大型地基望遠鏡結構尺度相對較大，將望遠鏡圓頂內的風速場表達為隨時間和空間位置變化的二維隨機場，通過引入互相關函數或互功率譜矩陣來刻畫隨機場的統計特征。基于互功率譜矩陣，采用譜表達方法實現時程模擬。為了克服在離散采樣點數提高時，譜表達方法中各個離散采樣點處互功率譜矩陣Cholesky 分解出現數值不穩定的問題，引入了文獻［15-17］所述波數譜方法，從而可以表達空間和時間頻率范圍內幾乎連續的隨機場。最后，對2 m 望遠鏡進行風速場模擬并在此風速場下進行性能分析。

2 望遠鏡結構動力學建模

2 m 級地基光學望遠鏡結構簡圖如圖1 所示，總體高度為6.4 m，寬度為3.7 m，總質量接近30 噸。從望遠鏡結構角度考慮，主要包括地平式機架、主鏡和次鏡三部分，其余附屬結構對本文所研究內容影響較小，在此不予考慮。

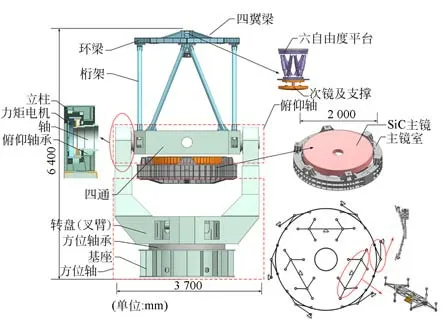
圖1 2 m 望遠鏡結構簡圖Fig.1 Simplified structure of 2 m telescope

自無窮遠目標發出的光束經過主鏡和次鏡反射后，被像面位置處的高靈敏度探測器接收，實現光信號到電信號的轉換，從而獲得清晰的目標圖像。地平式機架是主、次鏡及其他附件的載體，通過俯仰軸和方位軸的高精度回轉運動實現望遠鏡對任意天區的精確指向和對目標的穩定跟蹤測量。

望遠鏡主鏡材料為SiC，具有比剛度大、質量輕、熱穩定性好等優點，采用A-Frame 型柔性側支撐方式，并結合18 點機械式whiffletree 軸向支撐方式，支撐結構原理如圖1 所示。同樣，次鏡采用具有熱變形匹配的bipod 型結構來消除熱膨脹系數差異性對次鏡面形精度的影響。此外，次鏡結構整體通過Hexapod 并聯機構實現位置調整與補償。

針對上述2 m 望遠鏡簡化結構，采用有限元方法建立望遠鏡結構動力學模型如圖2 所示。在全局坐標系下，望遠鏡結構動力學模型可以表達為二階微分方程，即：

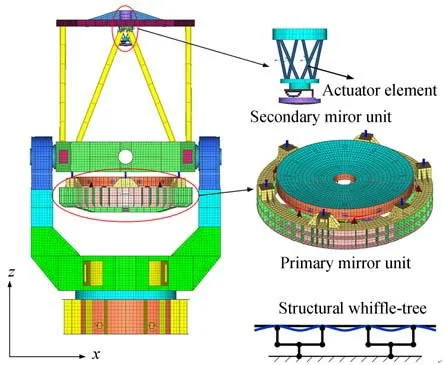
圖2 2 m 望遠鏡結構有限元模型Fig.2 Finite element model of 2 m telescope structure

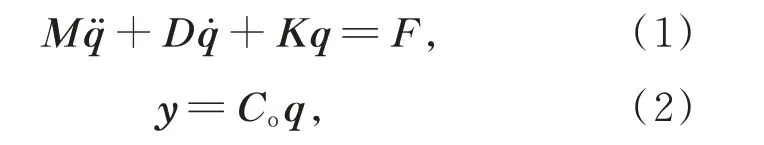
其中：M，D，K分別為質量矩陣，阻尼矩陣和剛度矩陣；F為載荷向量；y為輸出位移向量；q¨，q˙，q分別為節點加速度，速度和位移向量；Co為輸出矩陣，在風擾動分析中，主要關注的是主、次鏡節點的位移，因此輸出矩陣為與主、次鏡節點位置相關的矩陣。

由于望遠鏡結構非常大，有限元模型節點數量非常多，上述以節點變量來表達的結構動力學模型將非常大。為了提高計算效率，降低后續風擾動模擬的計算難度，對結構動力學模型進行模態變換，即

其中，Φ為振型矩陣，其表達式為：

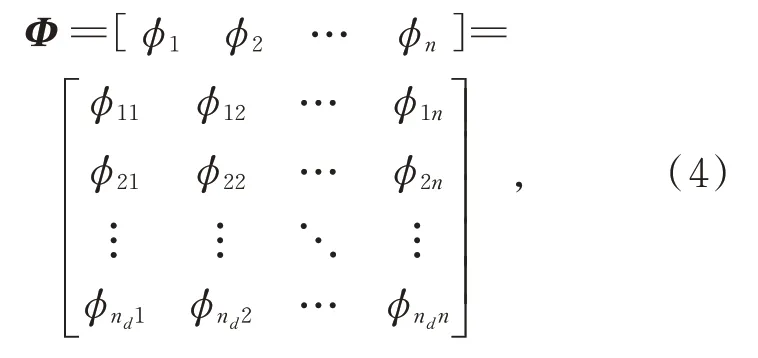
其中：φij表示第i個節點自由度上的第j階振型；nd為模型階數，即節點的全部自由度總和；n為提取的模態階數。

將式（3）帶入式（1）和式（2），并在式（1）左乘ΦT得：

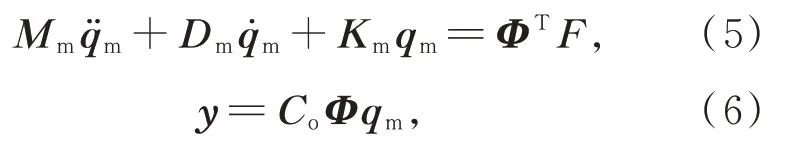
其中：Mm=ΦTMΦ，Dm=ΦTDΦ，Km=ΦTKΦ。

對以模態變量表達的結構動力學方程（5）和（6）進一步簡化可得：

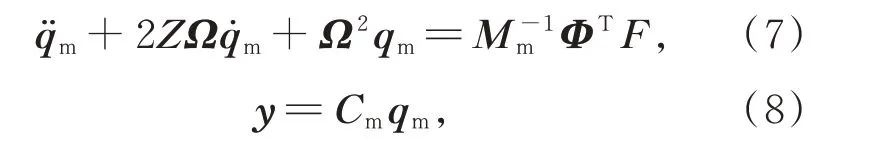
其 中：Z=diag(ζ1，ζ2，…，ζn)為 阻 尼 系 數 矩 陣，Ω=diag(ω1，ω2，…，ωn)為模態頻率矩陣，Cm=CoΦ。

為了應用線性系統相關理論，將式（7）和（8）表達的結構動力學模型轉化為狀態空間表達形式。定義狀態變量為：

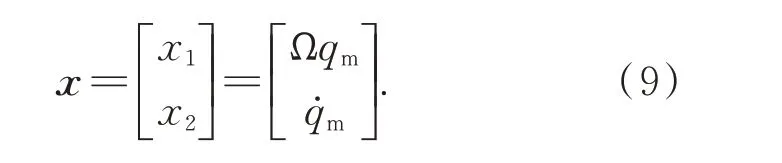
將式（9）帶入式（7）和（8）可得：

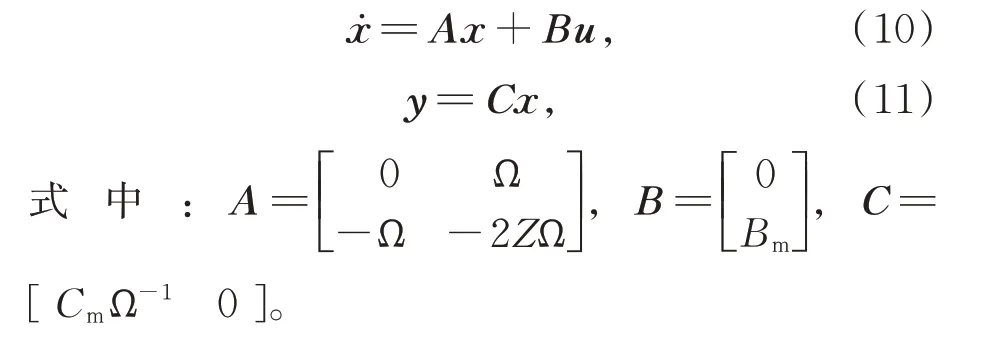
與式（1）和（2）相比，狀態空間方程（10）和（11）表達的結構動力學模型的維數大大降低，從而可以顯著提高計算效率。

3 隨機風擾動建模

對于地基大型光學望遠鏡而言，風擾動的直接影響是造成望遠鏡視軸抖動及光學元件（主要是主鏡和次鏡）的振動和變形，進而導致焦面處圖像抖動和模糊。風擾動具有隨機性，作用在望遠鏡結構上產生的變形非常復雜，即使采用計算流體動力學分析方法CFD 也很難準確模擬［7］。為了簡化計算模擬過程，本文將風擾動對望遠鏡的作用簡化為如圖3 所示的三種方式：（1）載荷作用在次鏡及其支撐桁架上，引起次鏡抖動；（2）載荷作用在主鏡及其支撐結構上引起主鏡變形和位置的變化；（3）載荷作用在次鏡及支撐桁架上，造成俯仰軸的擾動，進而引起視軸抖動。風擾動的綜合作用效果是引起主、次鏡光軸相對位置出現偏差，鏡面出現面形誤差以及視軸抖動，進而造成光學系統性能下降。

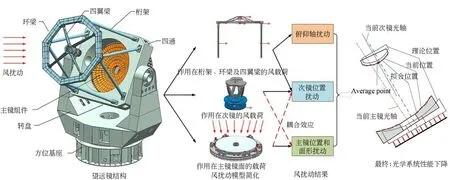
圖3 風擾動作用簡化模型Fig.3 Simplified model of wind disturbance

3.1 基于二維隨機場的風速時程模擬

從圖1 已知望遠鏡的橫向和縱向最大跨度相對較大，分別為6.4 m 和3.7 m，對風速進行時程模擬需要同時考慮時間頻率和空間頻率，且空間頻率需要考慮多個維度。這里提出了以平面內的二維隨機場來模擬作用在望遠鏡結構上的風速，風速在空間上任何一點的時間歷程上既具有隨機性又符合統計規律，其功率譜與預先已知的功率譜密度一致。首先推導一維隨機場，然后再將其拓展至二維情況。

定義X（t）為離散且相互獨立的隨機過程向量，即：

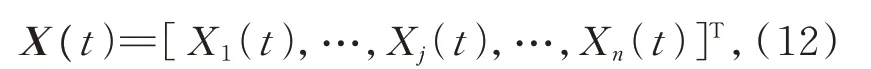
其中，Xj(t)為第j個單變量隨機過程。

隨機過程向量中的各元素均為相互獨立的單變量隨機過程，但作為一個整體，不同元素之間存在一定的相關關系，可以用互相關函數矩陣或互功率譜密度矩陣來表示，即：

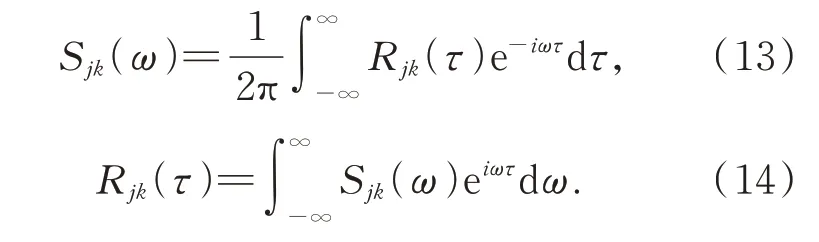
為了從時程角度模擬隨機過程，首先需要對其互功率譜密度矩陣進行分解，即：

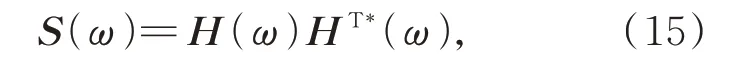
其中：H（ω）為下三角矩陣，T*表示復共軛轉置，上述分解可以通過Cholesky 方法實現。

根據式（15），隨機過程向量X（t）的時間歷程可以表達為：

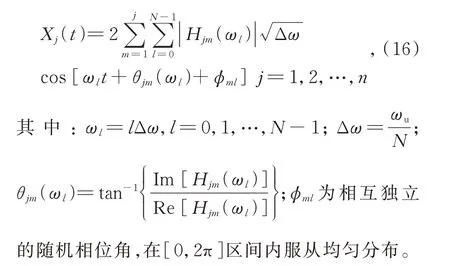
盡管式（16）給出了隨機過程向量的時間歷程顯式表達式，但當采樣點數N→∞時，功率譜密度矩陣接近奇異，無法應用Cholesky 方法對其進行分解。為了解決該問題，本文引入波數譜，建立在空間和時間上幾乎連續的風速模型，這可以在規定空間范圍內得到無窮采樣點的風速，從而避免了互功率譜矩陣的Cholesky 分解。波數譜的表達式可以由自功率譜和相干函數積分得到，即：

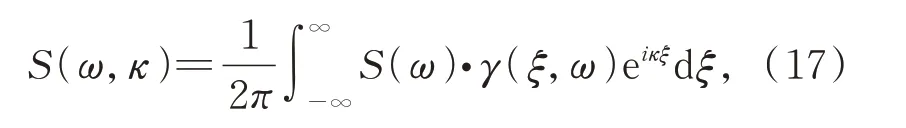
其 中，S(ω)為 自 譜，ξ為 空 間 距 離，κ為 波 數，γ(ξ，ω)為相干函數，通常選擇Davenport 相干函數模型。

基于波數譜（17），可以得到隨機過程向量X（t）的時間歷程表達式為：

式（18）僅給出了考慮一維空間頻率和時間頻率的表達式。然而，對于望遠鏡來說，尤其是對于大口徑主鏡來說，風速模擬時考慮平面內二維空間頻率更合理。為此，需要將式（18）拓展至二維空間頻率范圍。

二維空間的波數譜可以由式（19）積分得到，即：

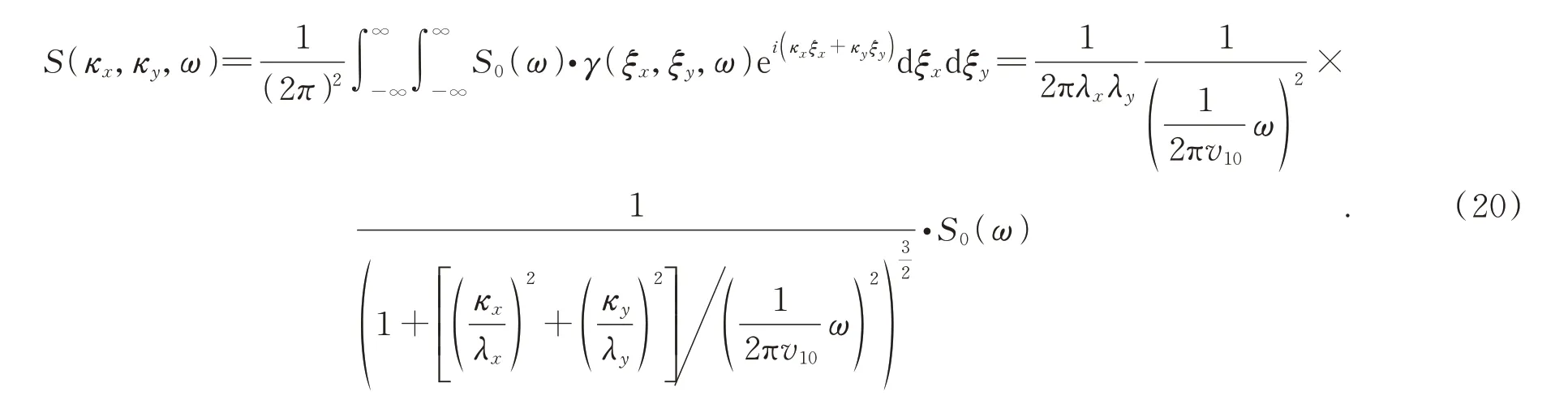
通常描述風擾動的功率譜選擇Davenport 功率譜，其表達式為：

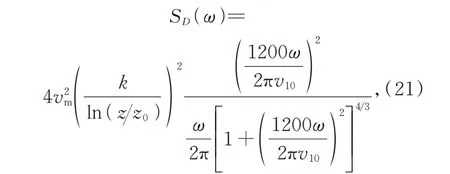
其中：vm為平均風速，k為風阻系數。

根據二維空間的波數譜表達式（20），可得二維空間隨機場的時程表達式為：

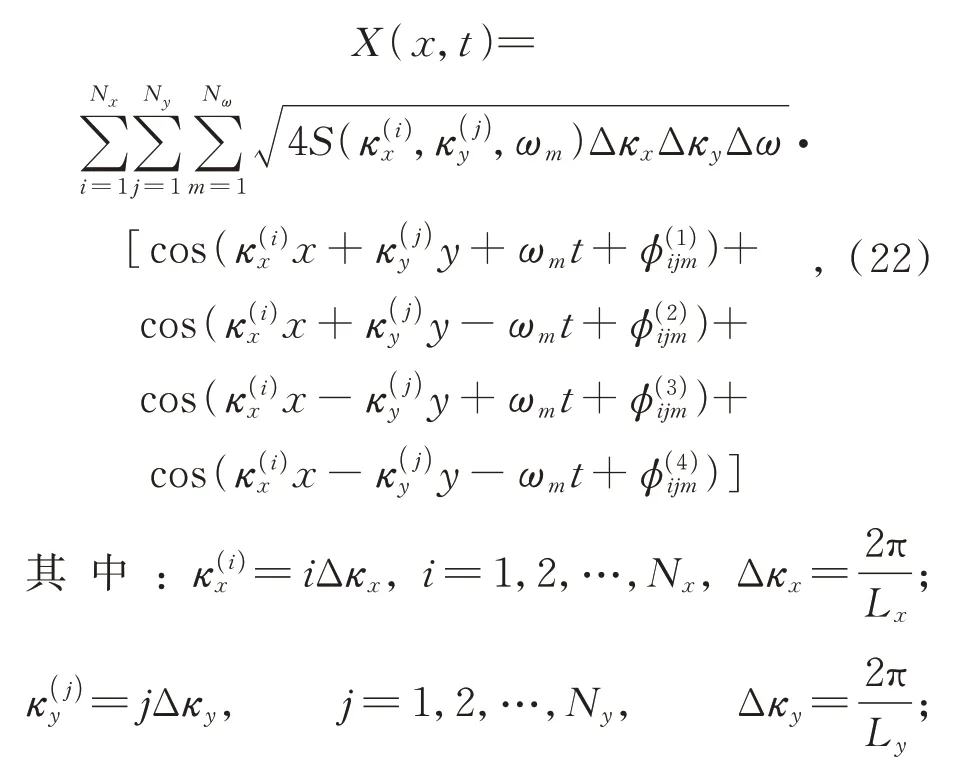
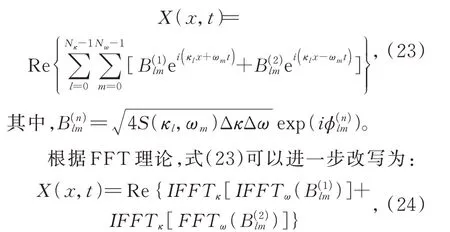
3.2 FFT 算法

式（18）和式（22）分別給出了一維空間和二維空間情況下的風速時程表達式，具有相同的表達形式，分別為二重和三重求和表達式。隨著采樣點數量的增大，計算效率將會顯著下降。為了改善計算效率，這里引入快速傅里葉算法FFT。

為了利用FFT，將式（18）改寫為：

其 中，FFT(·)和IFFT(·)分 別 表 示 快 速 傅 里 葉 變換和逆變換。

同樣，式（22）可以變換為：

對比式（26）和（22）可以發現，通過引入FFT算法，空間頻率和時間頻率的多重求和被FFT算法代替，從而顯著改善了風速模擬的計算效率。

3.3 風載荷計算方法

從前面推導已知風速具有隨機變化的特征，風速的幅值v可以表達為常量或平均風速vm和大氣湍流引起的時變量Δv之和，即：

風載荷的表達式為：

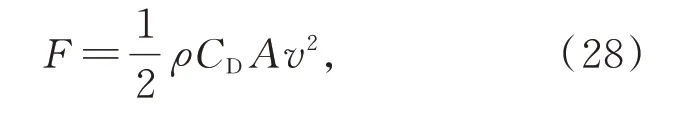
其 中：ρ為 空 氣 密 度，CD為 風 阻 系 數，A為 迎 風面積。

同樣，風載荷也可以分解為穩態量和非穩態量的和，即：

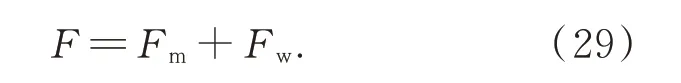
非穩態風載荷Fw與Δv有關，通過對（28）Taylor 展開可得：

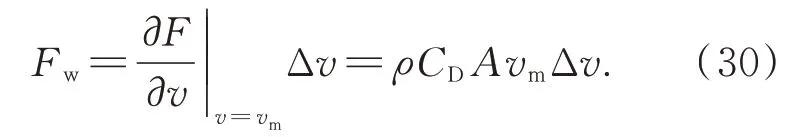
望遠鏡結構非常復雜，作用在望遠鏡上的風載荷也同樣非常復雜。從望遠鏡結構的角度，主要考慮圖3 所示的三方面作用，即主鏡、桁架以及環梁和次鏡上的風擾動作用。為了簡化分析計算難度，將望遠鏡劃分為三層，如圖4 所示，以這三層的位置來離散采樣點，然后根據式（30）來計算風載荷，并根據結構狀態方程（10）和（11）來計算風擾動響應。

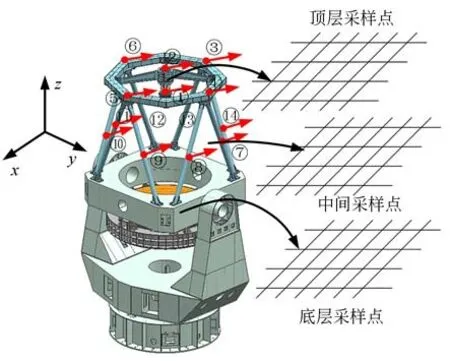
圖4 望遠鏡上的風載荷Fig.4 Wind load acting on telescopes

4 數值算例

以圖1 所示的2 m 口徑地基望遠鏡為例，采用本文提出的基于二維隨機場的風擾動建模方法模擬望遠鏡的風擾動環境，并與已有文獻進行對比，其中與望遠鏡結構相關的參數如表1 所示。此外，對隨機風擾動對望遠鏡的影響進行了詳細的仿真分析并對光學性能進行預測。

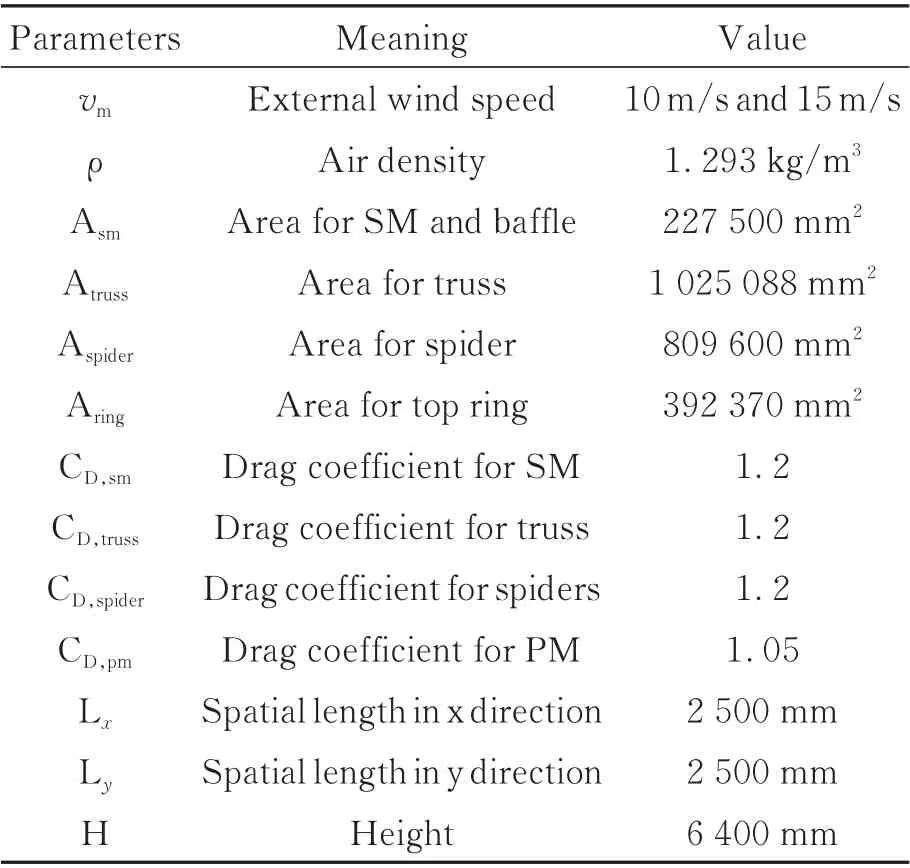
表1 風載荷計算參數Tab.1 Parameters of wind load

4.1 隨機風擾動的模擬與驗證

根據3.2 節所述二維隨機場的理論，按圖4所示將作用在望遠鏡的隨機風速場簡化為三層離散網格并在這些網格點生成隨機風速數據，隨機風速場離散參數如表2 所示。以主鏡為例，在主鏡鏡面位置按圖5 所示隨機采樣6 個位置，外界平均風速10 m/s 情況下，風速的時程變化過程以及相應的功率譜如圖6 所示。

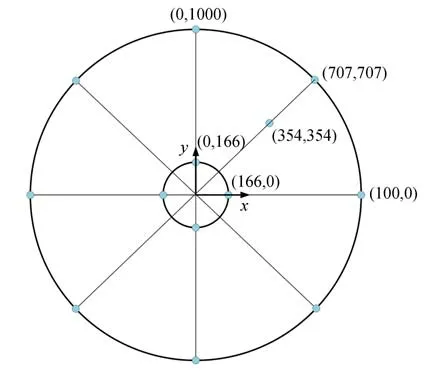
圖5 主鏡采樣位置Fig.5 Sampling points of the primary mirror

表2 風速場離散參數Tab.2 Discretized parameters of wind speed fields

從圖6 所示的主鏡上6 個采樣點位置的風速時程變化曲線以及功率譜曲線可以得出以下結論：

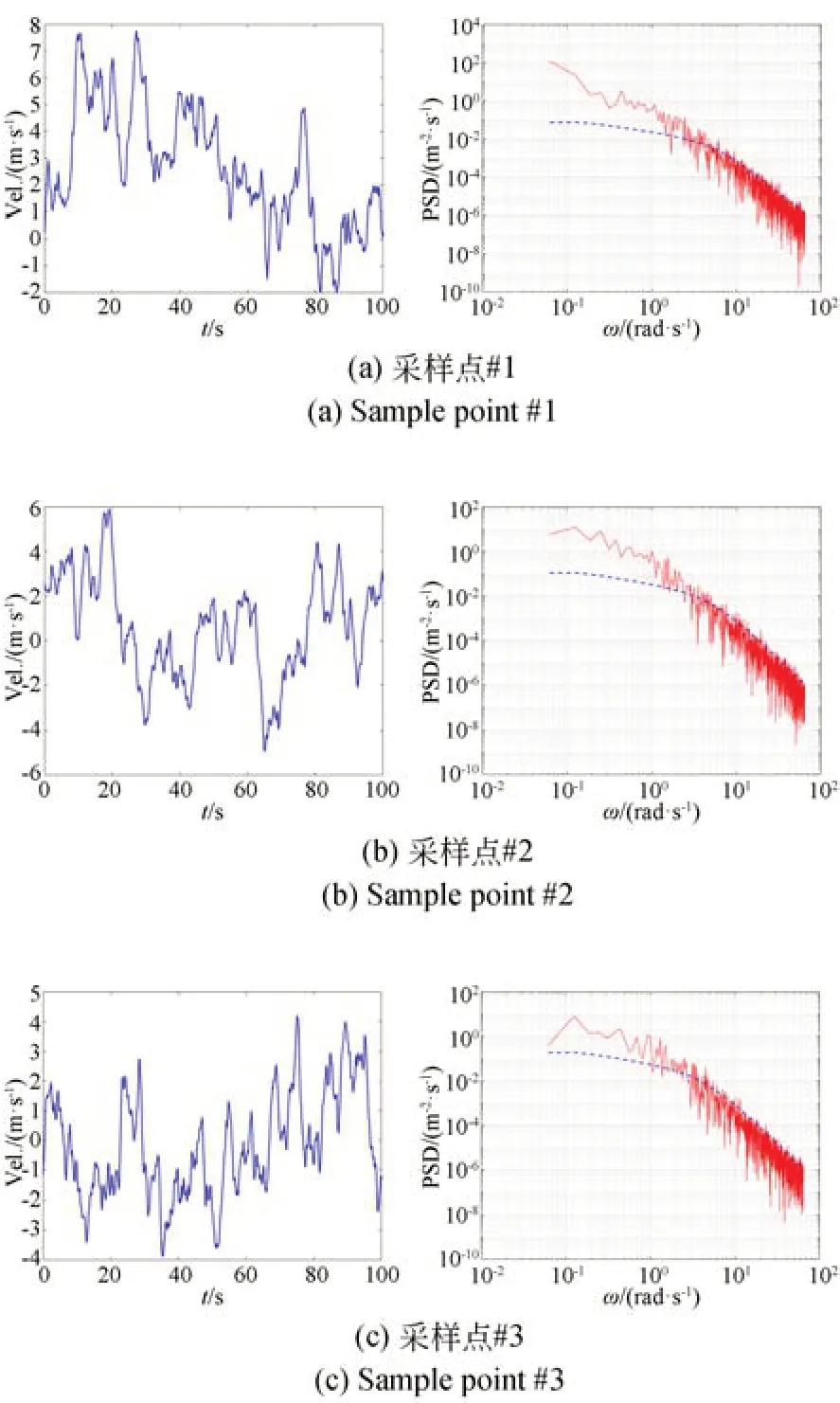
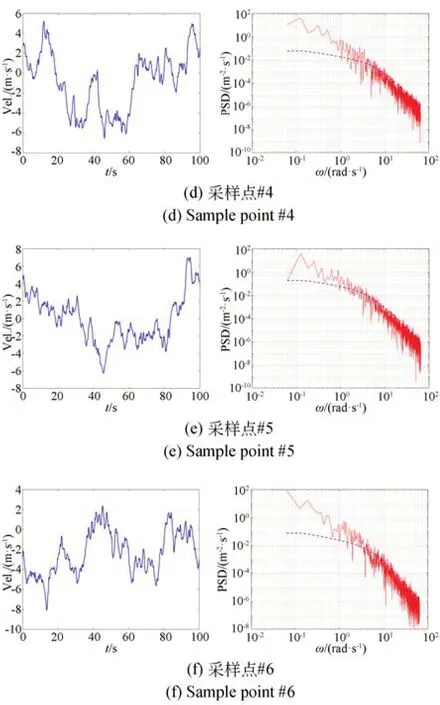
圖6 主鏡各個采樣位置的風速Fig.6 Wind speed for each sample point of the primary mirror

（1）從時間歷程上看，各個采樣點的風速均隨時間隨機變化；

（2）在模擬時長范圍內，各個采樣點風速時程的功率譜與初始給定的Davenport 功率變化趨勢基本一致，且與文獻［18］給出的結論相符。

從以上結論可以看出，基于二維隨機場理論而生成的風速場具有空間和時間隨機性的特征，這與實際望遠鏡使用環境中風速的湍流特性是基本一致的，以此來模擬實際中的風速環境是合理可行的。

4.2 風擾動分析及光學性能預測

利用4.1 節給出的隨機風速場，按3.3 節所述的計算方法得到平均風速10 m/s 和15 m/s 情況下風載荷時間歷程數據，并加載到望遠鏡結構動力學模型中，即可模擬出望遠鏡上各個位置的風擾動響應。由于望遠鏡工作中主要關注光學系統性能，而光學系統主要受主、次鏡的鏡面面形以及相對位置影響，因此在性能模擬與預測時主要考慮主、次鏡鏡面節點位置的動態變化情況。根據離散節點位置變化，采用非線性最佳擬合的方法計算主、次鏡鏡面面形精度以及相對空間位置，具體計算方法可參考文獻［19］，并以此來評估風擾動對望遠鏡的影響。

在風擾動模擬時，將主鏡與次鏡及桁架分開考慮，這樣有利于詳細分析主鏡與次鏡及桁架之間的相互耦合關系。在主鏡單獨作用風載荷情況下，主、次鏡鏡面面形精度變化如圖7 所示，光軸角度變化如圖8 所示，主、次鏡相對位置偏差如圖9 所示。

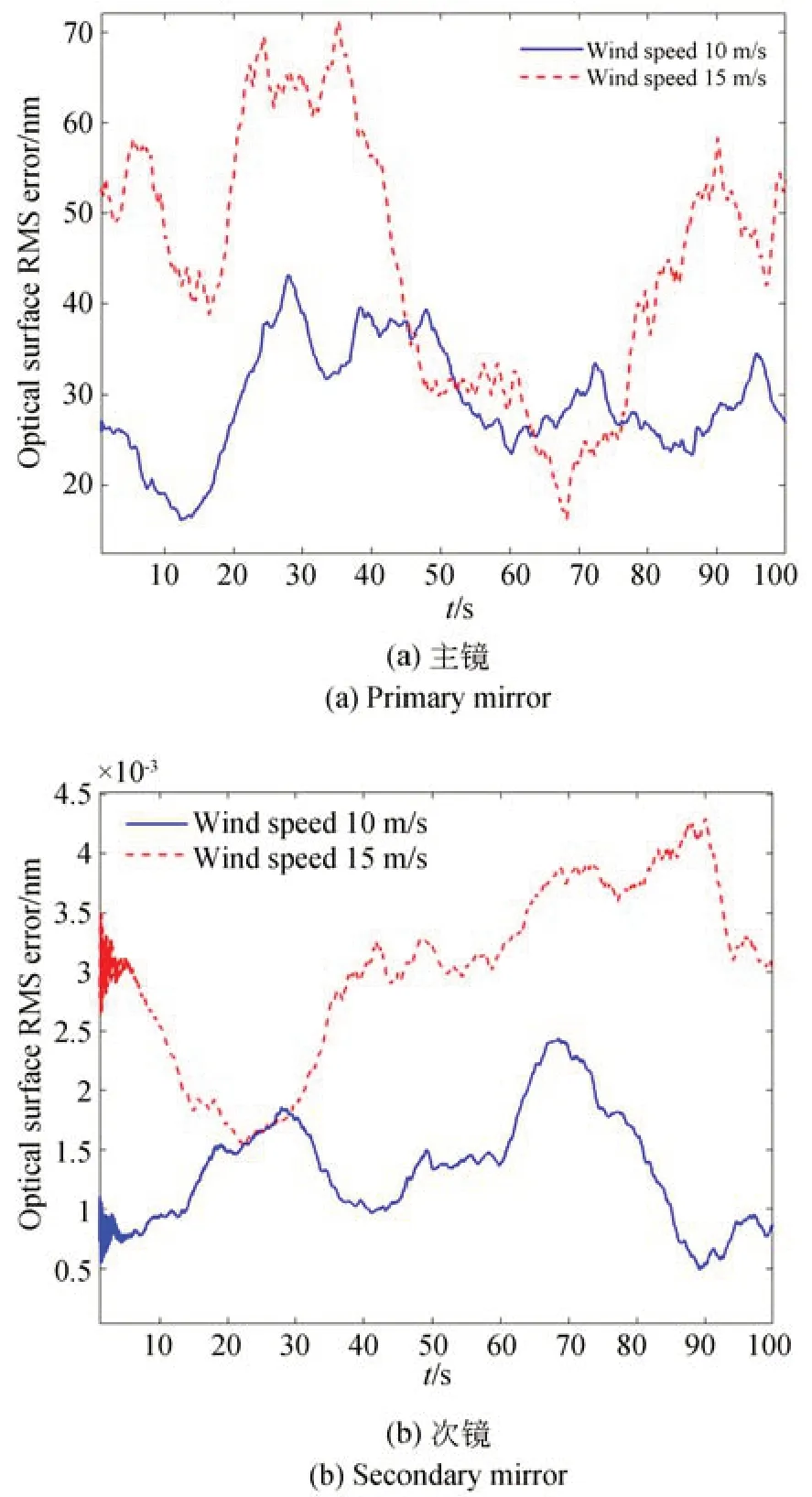
圖7 主鏡和次鏡鏡面面形精度-主鏡單獨加載Fig.7 Surface precision of the primary and secondary mirror-primary mirror loaded separately

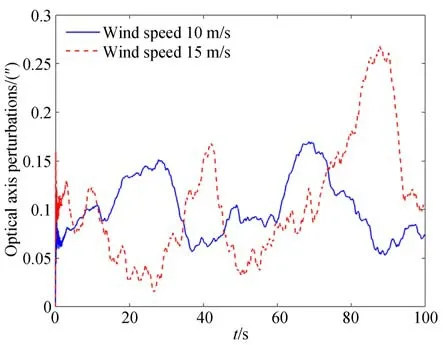
圖8 主鏡和次鏡光軸角度-主鏡單獨加載Fig.8 Optical axis perturbation of the primary and secondary mirror-primary mirror loaded separately

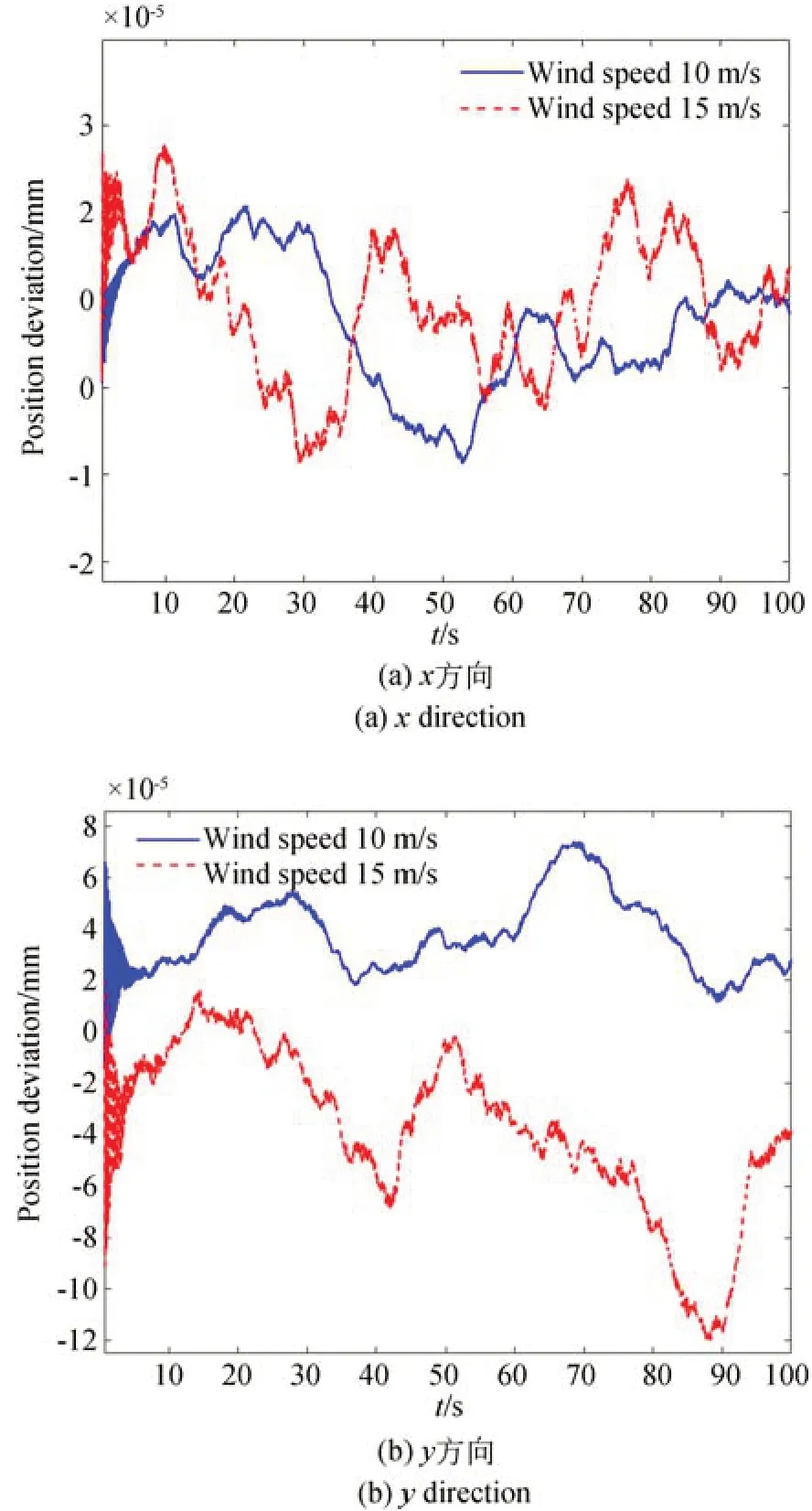
圖9 主次鏡位置偏差-主鏡單獨加載Fig.9 Position deviation of the primary and secondary mirror-primary mirror loaded separately

在主鏡單獨作用10 m/s 和15 m/s 風擾動載荷情況下，主鏡的面形精度影響很大，最差面形精度分別達到了45 nm 和70 nm，而次鏡面形精度基本不受影響；主、次鏡光軸角度偏差最差時分別達到0.15″和0.25″，對相對位置偏差幾乎沒有影響。

在次鏡及桁架單獨作用風載荷情況下，主、次鏡鏡面面形精度變化如圖10 所示，光軸角度變化如圖11 所示，主、次鏡相對位置偏差如圖12所示。

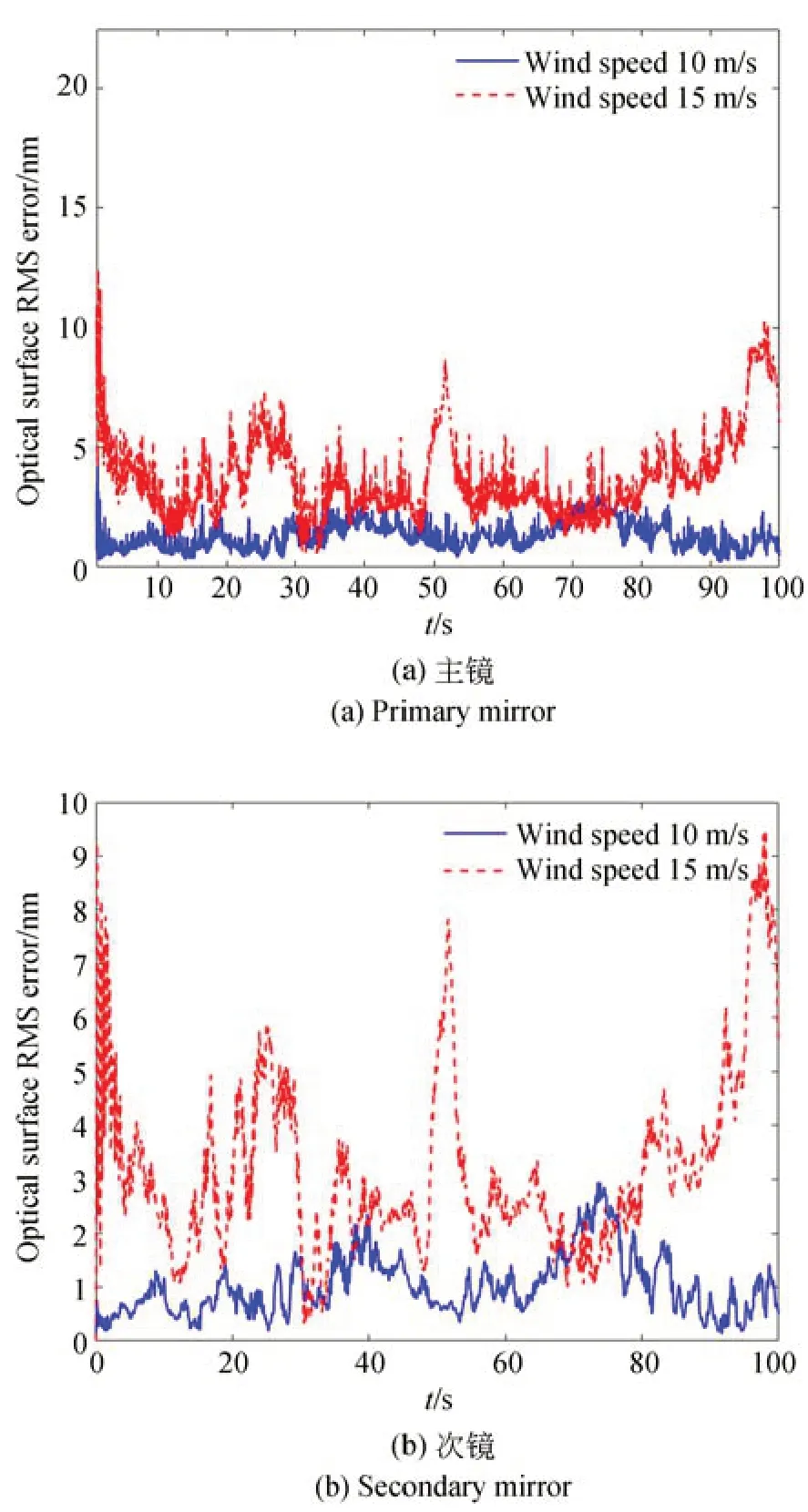
圖10 主鏡和次鏡鏡面面形精度-次鏡及桁架單獨加載Fig.10 Surface precision of the primary and secondary mirror-secondary mirror and truss loaded separately

在次鏡及桁架單獨作用風載荷情況下，主鏡面形精度受影響相對較小，在整個仿真時段均在5 nm 左右；而次鏡面形精度變化同樣很小，原因在于次鏡口徑較小；主次鏡光軸角度較前一種工況增加幅度很大，初始階段最大偏差接近8″～10″，剩余階段在4.5″以內，但波動頻率明顯提高；同樣主、次鏡y向相對位置偏差增加幅度很大，分別達到了0.1 mm 和0.2 mm。對圖11 和圖12（b）所示數據進行FFT 變換得到頻譜如圖13 所示。從頻譜曲線中可以看出，風擾動載荷對望遠鏡的影響集中在低頻部分，約0～5 Hz 區域，高頻分量的影響較小。

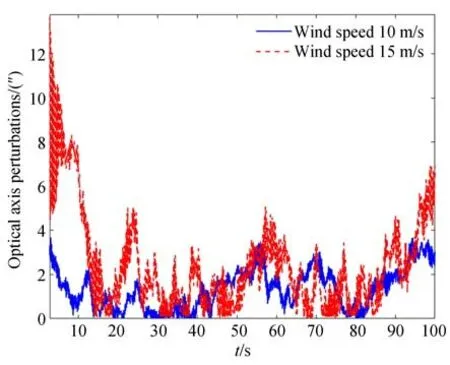
圖11 主鏡和次鏡光軸角度-次鏡及桁架單獨加載Fig.11 Optical axis perturbation of the primary and secondary mirror-secondary mirror and truss loaded separately

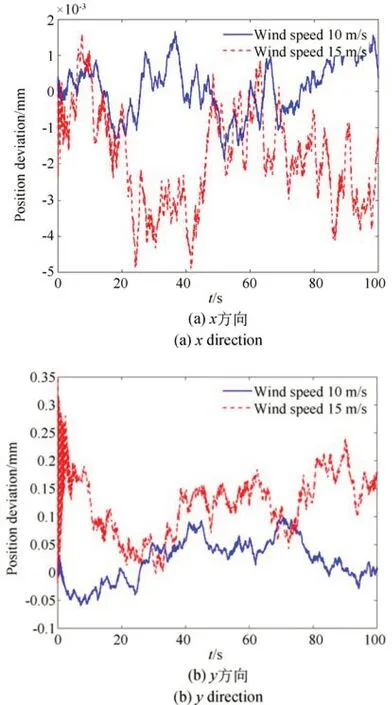
圖12 主鏡和次鏡位置偏差-次鏡及桁架單獨加載Fig.12 Position deviation of the primary and secondary mirror-secondary mirror and truss loaded separately

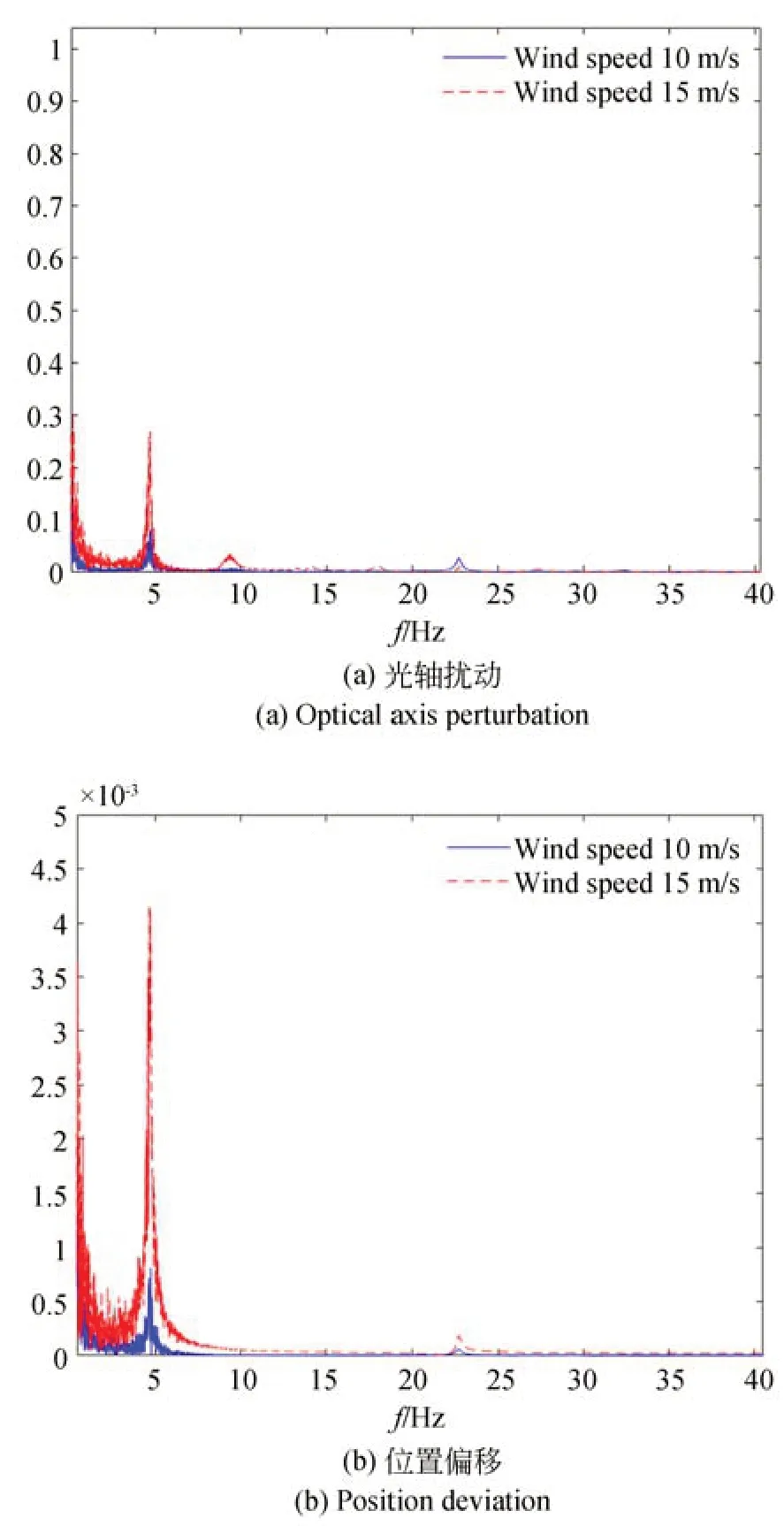
圖13 主次鏡偏差頻譜-次鏡及桁架單獨加載Fig.13 Frequency spectrum of position deviation between primary and secondary mirror-secondary mirror and truss loaded separately

從以上兩種情況下的分析結果對比中可以得出以下結論：

（1）由于次鏡口徑較小，相對剛度較大，風擾動對次鏡面形精度影響較小；

（2）主鏡面形精度變化主要來源于作用在主鏡鏡面的風載荷，受次鏡及桁架的影響較小，即主、次鏡相互耦合較小；從望遠鏡結構特征角度看，主鏡連同主鏡室以及桁架分別連接在四通下表面和上表面，而四通本身剛度很大，因此相互耦合不明顯的結果是合理的；

（3）次鏡及桁架單元作用風載荷時，主、次鏡光軸角度偏差以及相對位置偏差明顯增大，將會導致望遠鏡光學系統成像抖動和模糊。

5 結 論

本文針對大型地基光學望遠鏡系統性能受風擾動影響顯著的問題，研究了風擾動的時程模擬方法并對望遠鏡在風擾動下的性能進行預測。利用有限元方法及模態變換，建立了望遠鏡結構動力學模型。基于二維空間隨機場，提出望遠鏡圓頂內風速的時程模擬方法，此方法可以表達空間和時間頻率范圍內幾乎連續的隨機場。對2 m口徑望遠鏡的仿真分析結果表明：在外界平均風速10 m/s 和15 m/s 情況下，隨機風擾動作用在望遠鏡主鏡上會造成主鏡面形變差，分別造成最大接近45 nm 和70 nm 的面形誤差；作用在次鏡及桁架上的風擾動主要造成低頻0～5 Hz 光軸角度誤差及主、次鏡相對位置偏差；主、次鏡之間相互耦合效應較小。