材料彈性影響的塑料齒輪齒根應力仿真分析?

袁卓俊 郭棟祥

（江蘇科技大學 鎮江 212100）

1 引言

通常設計齒輪時，首先要對齒輪強度進行核算。對于齒輪齒根應力計算方法，最早于1893年，Lewis［1］將輪齒視為懸臂梁，以此為基礎計算齒根應力值。此后，基于Lewis懸臂梁理論的齒輪齒根應力計算方法被多數國家標準采用。現有標準［2～4］的齒輪齒根應力計算里，應力值取決于齒輪的齒形、結構參數、工況條件，與材料屬性無關。但在文獻［5］里，D Walton闡述了非金屬齒輪由于彈性模量小，在變形影響下會導致齒輪實際重合度增大的可能性；在文獻［6］與［7］中，Christian Hasl與Jabbour分別嘗試以現有標準為基礎，擬定一種考慮實際重合度增大引起的塑料直齒輪與塑料斜齒輪齒根應力計算方法。

本文采用ANSYS Workbench軟件，對鋼-塑料齒輪副單齒嚙合模型的塑料齒輪齒根應力仿真分析，通過改變不同的彈性模量值，以及考慮輪齒撓曲變形的影響，計算不同材料彈性屬性的塑料齒輪在一定負荷下的齒根應力。

2 試驗參數與條件

齒輪參數如表1所示，齒輪副為外嚙合標準漸開線直齒圓柱齒輪，常溫下工作。材料參數如表2所示，塑料材料的泊松比范圍μ?(0.3，0.5)，這里取泊松比值μ=0.4。齒輪副參數不變，彈性模量選取1000Mpa～4000Mpa范圍內的4個數值，主動輪施加的扭矩T1選取0.06Nm～8Nm范圍內的6個數值，應用ANSYS Workbench軟件進行仿真試驗。

表1 齒輪參數

表2 材料參數

3 基于VDI 2736標準的塑料齒輪齒根應力計算

根據VDI 2736塑料齒輪強度計算標準，齒根應力有下列計算式：

查詢VDI 2736標準的圖表數據，通過確定式中參數，可以計算得σF2≈33.5T1。其中主動輪施加扭矩T1單位為Nm，塑料齒輪的齒根應力σF2單位為Mpa。

4 考慮材料彈性影響的齒根應力有限元法

聯合應用Creo與ANSYS Workbench軟件，根據表1的齒輪參數，建立齒輪單齒嚙合模型，并定義表2的材料參數；然后對模型用六面體網格整體劃分；最后在塑料齒輪齒根部位網格細化，如圖1所示，經過網格劃分后的模型，共有59048個節點和37801個單元。

圖1 網格劃分

在軟件中，兩個零件的接觸分為接觸體與目標體，鋼齒輪與塑料齒輪接觸，比較軟的塑料齒輪為接觸體，而較硬的鋼齒輪為目標體，輪齒接觸區需要考慮到塑料會出現的大變形，選用增廣拉格朗日法，可以使這種大變形問題計算更容易收斂。塑料齒輪輪齒的底面固定約束，對齒根兩側面無摩擦支撐；鋼齒輪作為驅動輪，應用Joint命令，僅釋放鋼齒輪輪齒繞Z軸轉動的自由度，施加的載荷與約束如圖2所示。此外，考慮在負荷下塑料齒輪模型產生的單元位移與形變，以及形變對有限元計算中剛度矩陣變化的影響，必須打開大變形開關。

圖2 施加載荷與約束

通過計算，可以得出塑料齒輪的最大變形量、左側齒根應力、右側齒根應力、最大齒根應力的取值，以及最大齒根應力相對VDI 2736標準值的偏差。

5 齒根應力的數值處理與結果分析

5.1 塑料輪齒的變形

塑料輪齒的變形如圖3所示，當塑料齒輪受到鋼制齒輪施加的扭矩時，塑料輪齒會呈現出一定的撓曲變形，其最大變形點通常在塑料輪齒的齒尖部位。將塑料輪齒的最大變形量記為s，繪制圖4曲線。圖中，當施加的扭矩很小時，不同材料彈性模量下塑料輪齒的變形相差不大；當主動輪施加的扭矩較大時，塑料材料的彈性模量越小，塑料輪齒越容易較大變形。

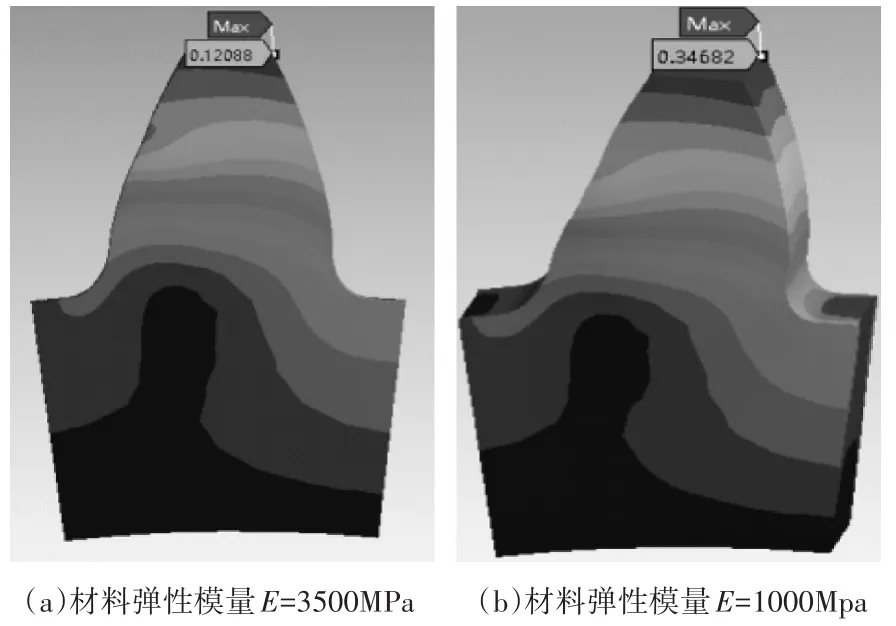
圖3 扭矩T1=6Nm時塑料輪齒的變形

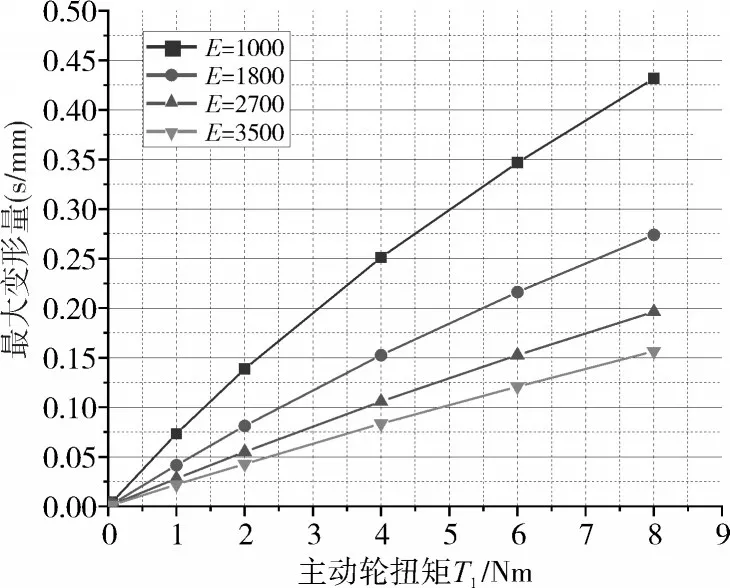
圖4 塑料輪齒的變形曲線圖

5.2 塑料輪齒的接觸

考慮塑料輪齒變形的影響，會使輪齒的接觸狀態出現相應變化。塑料輪齒的接觸如圖5～6所示。圖5～6可以看出：主動輪施加扭矩T1一定時，選用較小彈性模量的材料，會使得塑料輪齒接觸面積增大；額外增大的接觸面積開始分擔部分應力，導致輪齒接觸面上最大應力點的位置與最大應力的數值發生改變，塑料輪齒上的載荷出現了重新分布。

圖5 扭矩T1=4Nm時輪齒接觸狀況

圖6 扭矩T1=4Nm時輪齒接觸區的載荷分布

5.3 塑料輪齒的齒根應力

在主動輪施加的扭矩作用下，塑料齒輪的輪齒左側齒根存在受拉的應力，右側齒根存在受壓的應力。以主動輪施加的扭矩T1為橫坐標，某一側的齒根應力σF為縱坐標，繪制曲線圖7。在圖7中，塑料齒輪兩側齒根處的應力具有一致的變化趨勢，但齒根受壓側的應力值普遍比受拉側的大，因此塑料齒輪最大齒根應力應取決于齒根受壓側。而無論是受拉還是受壓，其兩者的應力值普遍比VDI 2736標準的理論計算值低。

圖7 塑料齒輪齒根應力

以主動輪施加的扭矩T1為橫坐標，最大齒根應力相對VDI 2736標準計算值的偏差為縱坐標，繪制圖8所示的偏差曲線。在圖8中，當施加的扭矩不大時，不同彈性模量下的偏差相對較小，其最小值在3%附近；如果主動輪施加的扭矩較大，則相對標準的偏差值會隨著選用材料彈性模量的減小而增大，本試驗研究中最大偏差達到18%左右。

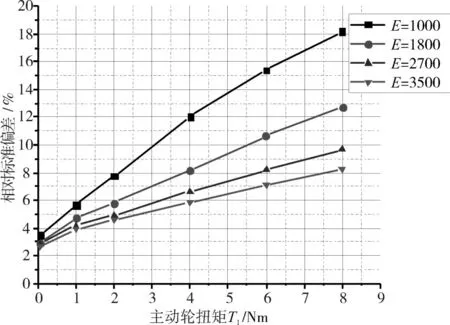
圖8 偏差曲線圖

相對偏差值的變化，這是由于VDI 2736標準計算，將齒輪視為了剛體模型，產生的形變忽略不計，這種假設對于鋼制齒輪來說是成立的。但是塑料輪齒的變形對齒輪應力的影響不可忽略，特別是較小彈性模量的齒輪材料，在撓曲變形影響下，塑料輪齒額外擴展的接觸區開始分擔部分應力，以及塑料輪齒上載荷的重新分布，導致齒根處的部分應力在一定程度上得到消除，如圖9～10所示，這會使塑料齒輪的齒根承載能力得以提高。

圖9 施加扭矩T1=4Nm

圖10 施加扭矩T1=6Nm

6 結語

應用ANSYS Workbench軟件對鋼-塑料齒輪副單齒嚙合模型仿真試驗，模擬不同塑料材料彈性模量數值下塑料輪齒的變形，以及對塑料齒輪齒根應力的影響，通過對比現有VDI 2736標準的塑料齒輪應力計算值，分析相對標準計算值的偏差來源。試驗結果表明：單齒嚙合時，施加扭矩一定，使用較小彈性模量的齒輪材料，塑料輪齒有更大的撓曲變形，導致輪齒接觸面積會出現額外的增大，額外增大的接觸面開始分擔部分應力，齒輪上的載荷出現了重新分布，齒根處的部分應力在一定程度上得以消除，這會使塑料齒輪的齒根承載能力得到提高。