一種基于多頻率單校準源的水下多元線陣陣形校準方法?

李光遠 王 瑩 王文冠 吳 迪

（大連測控技術研究所 大連 116013）

1 引言

隨著固定式噪聲測試技術及裝備的不斷發展，固定式水下多元陣列逐漸成為了艦船水下噪聲測量的重要手段，可為艦船噪聲源精確定位及識別提供可靠的平臺。然而，對于固定式布放于試驗場區的水下多元陣列噪聲測試系統，由于陣列規模較大，受布放施工誤差及海洋環境（海風、海流、海底地形）的影響，將不可避免地產生布放誤差，而陣列的布放誤差將直接導致基于理想陣形狀態下的噪聲源定位識別算法性能急劇下降［1］。一直以來，水下噪聲源精細化定位識別的主要手段是采用波達方向估計（Directional of Arrival，DOA）方法［2］，實現對噪聲源方位的精確分辨，其主要方法為基于特征分解理論的子空間類超分辨算法，典型的如多重信號分類算法［3］、信號參數旋轉不變算法［4］等，可初步解決艦船噪聲源精細化識別問題。隨著相關理論研究的不斷深入，研究人員又先后提出了波達方向矩陣算法［5］、加權子空間擬合方法［6～7］等，極大地提升了DOA算法精度。但在實際應用中，上述方法大多基于絕對精確的陣列流形，即各陣元間精確的位置關系。即使陣元位置存在較小偏差，DOA估計方法的性能都可能會急劇下降甚至失效［8］，因此，采用有效的措施對陣形進行校準成為了相關領域研究的關鍵和熱點。

目前存在許多陣形估計校準方法，然而由于它們各自的局限性，在實際使用過程中往往效果不佳。傳感器直測法可實時、快速校準陣列各陣元位置誤差，但此種算法的校準精度受到傳感器本身數量和精度的限制，且會導致系統穩定性降低［9］，只適合作為大尺度空間陣列的輔助校準手段。基于水聲同時基測距定位的陣形校準方法，主要利用水聲測距系統，結合基線定位理論，可解算出任意陣元的空間位置坐標，進而實現陣形校準［10］。該方法在實際應用中受海洋聲場及測距系統精度影響較大。利用校準源進行陣列校準主要包括有源校準方法和自校準方法［11～12］，上述方法可利用多個方位參數已知或未知的校準源信號聯合處理，并構建代價函數，進而實現對陣形的在線校準。但在實際應用過程中，用于校準的信號源往往體積較大，在實際應用中移動及操作不便，導致校準效率較低。針對此問題，提出一種基于單校準源的陣形校準方法，該方法將校準源放置在某一特定位置，通過改變校準源信號頻率，使信號分別符合遠場及近-遠場模型，代入對應的代價函數中聯合處理，完成陣形校準。仿真結果表明，該算法具有較好的穩健性和較高的估計精度。

2 模型構建

實際應用中，固定式多元線陣是噪聲源定位與識別的重要手段，廣泛應用于港口警戒、艦船噪聲源識別、目標特性獲取等相關領域。因此，本文以直線陣列為例構建陣列模型，定義以陣列中首陣元為原點建立坐標系，設定校準源到陣列參考陣元距離為ρ1，與陣列的陣元夾角為θ，陣元數目為N，陣列孔徑為為陣列各陣元的笛卡爾坐標，建立信號模型為x(t)=A*s(t)+n(t)，當校準源處于近-遠場時，信號可看做球面波，有：

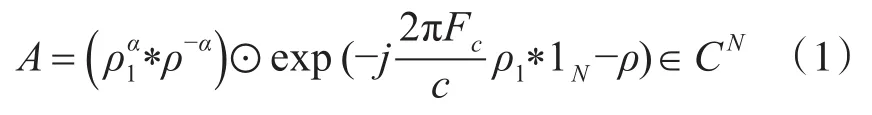
這里α為路徑損失常量，c為聲速。其中：

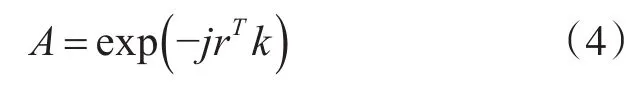
由式（1）～（4）可知，通過調節校準源頻率Fc，可使校準源分別處于陣列的遠場及近-遠場，并建立不同的陣列信號模型，通過對兩種模型的聯合處理，可實現對陣形位置誤差的校準。

對于布放于水下的固定式大尺度空間陣列，各陣元實際位置坐標為：其中為陣列的理論坐標，?為陣列的位置擾動。陣列實際陣列流形為，來源于已知位置的校準源信號功率為Ps，則協方差矩陣，其中Rnn可看做高斯白噪聲的協方差矩陣。已知特征值對應的特征向量可擴展為相同的線性空間，且有：，對于平面波，，對于球面波，有

3 陣形校準方法

考慮到實際布放的多元直線陣列，以首陣元為基準點建立坐標系，校準源與首陣元的距離為ρ1，角度為θ，假設校準源發射信號頻率為FC1，使校準源處于系統遠場，此時有：

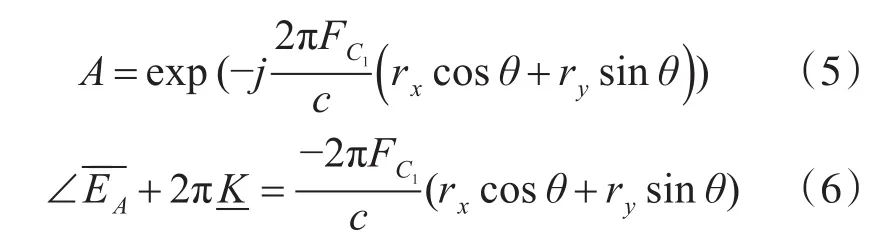
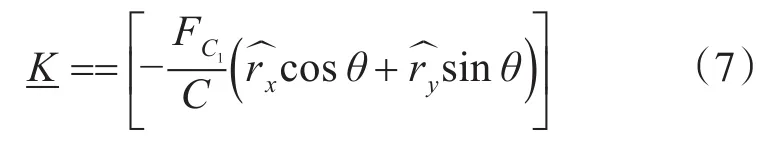
因此，式（6）可寫作：

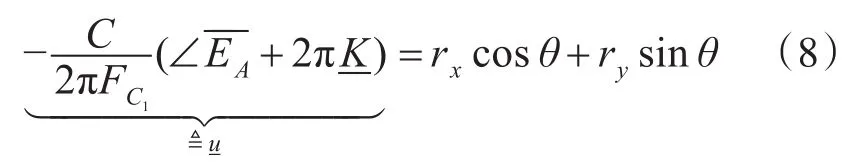
其中rx和ry為陣列各陣元的實際坐標。

接下來保持校準源位置不變，改變校準源發射信號頻率為FC2，使校準源符合近-遠場模型，信號可看做球面波，其模型符合式（1）。截取信號快拍數為L，有N*L維信號：

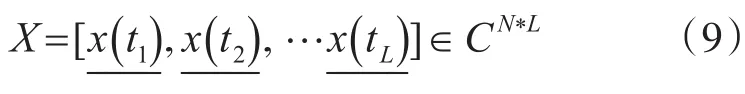
以各個陣元分別作為基準點進行運算，可得到N個協方差矩陣如下，其中第i個協方差矩陣，其中，由文獻［13］可知：

這里λi為Ri中最大的特征值與其他N-1個特征值的平均數的差值。ρi為校準源到第i個陣元的距離。，可推導出為校準源到各陣元的實際距離。結合（3）可知：

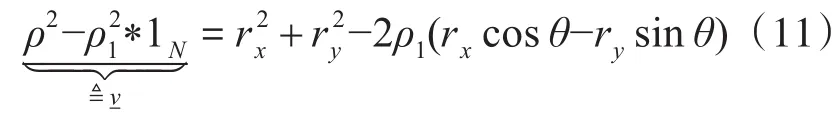
結合（8）、（11），可推導出：

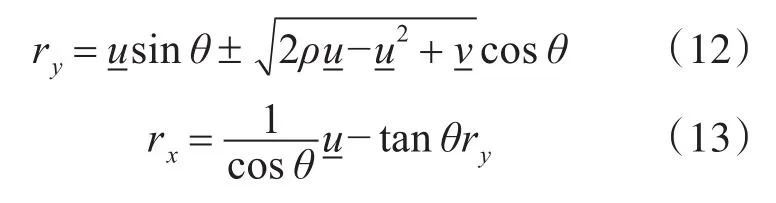
上述推導可得出以下結論：式（12）及（13）可分別得到兩個解，其中與理論位置更接近的解可看做校準后陣元的實際位置；該方法需要校準源至少提供兩種頻率的信號，一種使校準源處于陣列的近-遠場，一種使校準源處于陣列的遠場。當然，校準源也可以提供更多頻率的信號，通過對結果的平均處理，可進一步提升算法的精度。

由上述論述可知，該算法的步驟如下：

1）當信號處于較低頻率FC1（此時信號可看做平面波），計算協方差矩陣Rxx和特征向量，再分別計算出K和u；

2）調節信號為較高頻率FC2（此時信號可看做球面波），解算出協方差矩陣Ri，并分別找到其對應的特征值λi；

3）利用ρ1解算校準源到各陣元的距離，再進一步解算出v；

4）利用式（12）、（13）解算出rx、ry。

4 仿真試驗

利用Matlab對算法進行仿真試驗驗證，建立陣列模型為9元直線陣列，陣元間距設計為2m，以首陣元為坐標原點建立二維坐標系，并為陣元位置坐標添加隨機誤差。設置校準源據首陣元距離為800m，校準源與陣列夾角為30°，根據系統遠場判別條件，校準源分別發射單頻信號，頻率分別為FC1=1500Hz，FC2=5000Hz ，聲速為c=1500m/s，快拍數L=10000；信號信噪比為20dB，各陣元理論位置坐標為，實際位置坐標分別為［Xi,Yi］，校準后位置坐標為遵循上一節中的步驟，利用單校準源校準方法對陣元位置坐標進行校準，校準結果如表1所示。

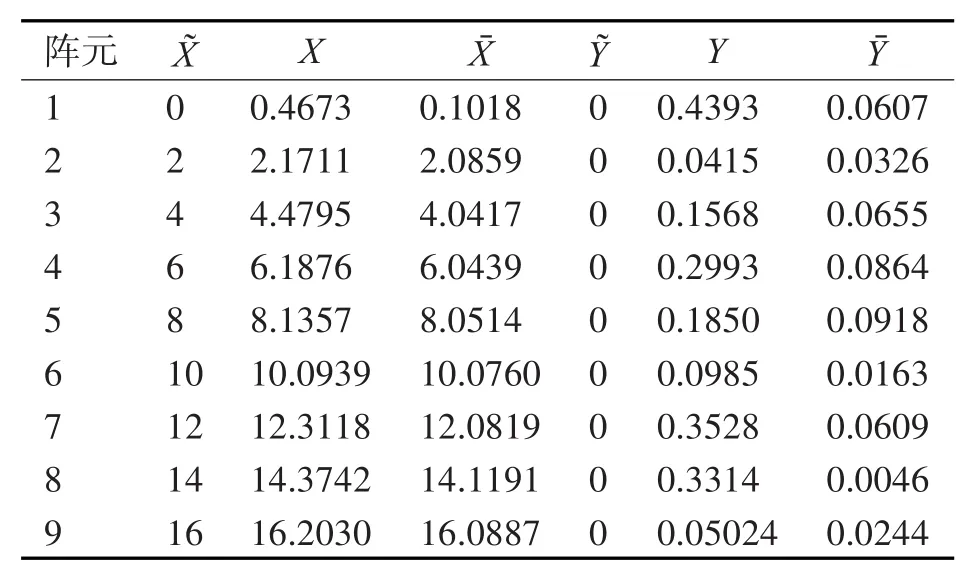
表1 位置誤差校準結果

完成對陣列位置誤差校準后，利用MUSIC算法，分別對理論陣列、陣形校準前陣列及陣形校準后陣列的DOA估計能力進行分析，假設信號源為3個，角度分別為［-10°，10°，30°］。校準結果如圖2所示。

如圖1、2所示，利用單校準源誤差校準方法，可有效完成對陣列位置坐標的校正，校正后的陣列與校正前的陣列相比，陣列性能大幅提高，證明該方法具有良好的校準精度，同時由于校準源位置不需要改變，可有效提升陣形校準效率。在上述基礎上控制信號源分別發射頻率為信號，以首陣元為坐標原點，各陣元第一次估計誤差分別為，平均后估計誤差分別為利用對不同信號組合的平均處理，可得到信號校準精度，平均處理后估計誤差如表2及圖3所示。結果可知，首次誤差校準后，各陣元誤差均小于0.12m，X方向平均誤差為0.076m，Y方向平均誤差為0.049m。平均處理后各陣元誤差均小于0.05m，其中X方向平均誤差為0.031m，Y方向平均誤差為0.025m。由此可見，通過平均處理后，該算法誤差估計能力大幅提升。

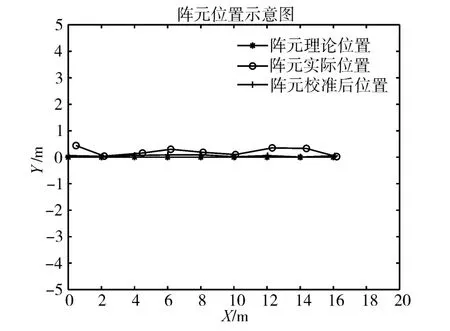
圖1 陣元位置示意圖

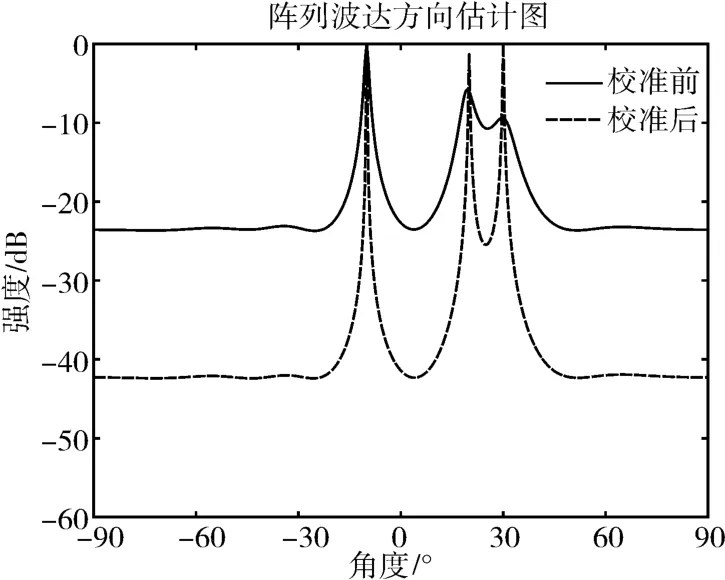
圖2 校正前后DOA譜圖

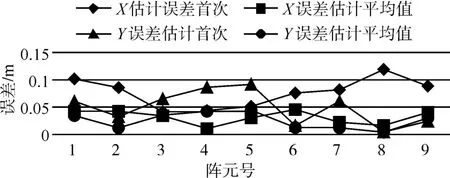
圖3 平均處理前后估計誤差值

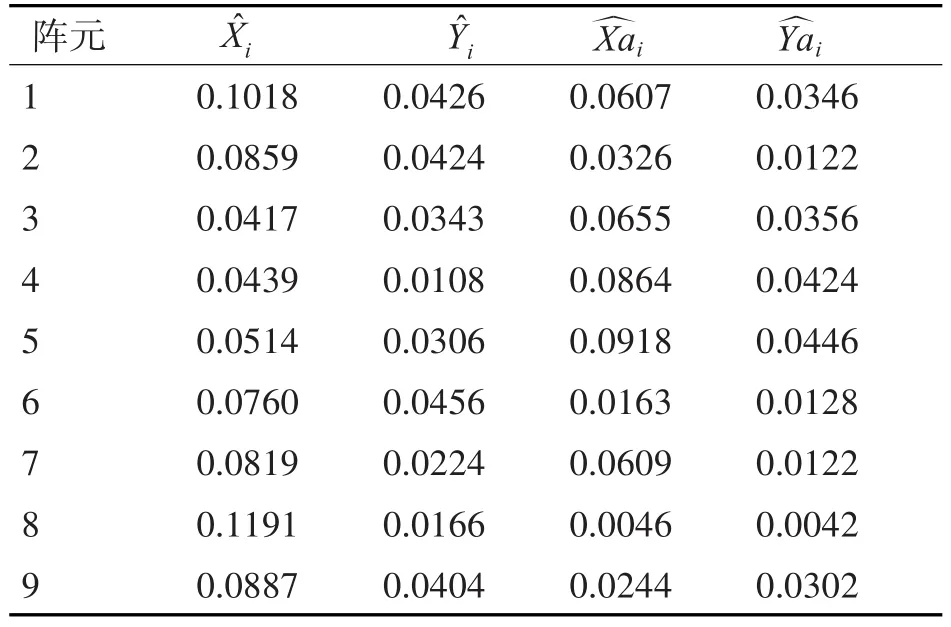
表2 平均處理前后估計誤差值

5 結語

本文提出了一種基于單校準源的水下多元陣列陣形校準方法，該方法通過設置位置已知的校準源發射至少兩種不同頻率的信號，使信號分別滿足陣列遠場及近遠場條件，并建立相應陣列信號模型。經過對代價函數的聯合處理，對陣元位置進行校正。通過增加不同頻率信號源信號，可有效提高算法估計精度。經Matlab方針仿真驗證可知，該方法可有效提升陣形校準效率，并可進一步推廣到其它形式的空間陣列，具有較好的應用前景。