垂直發射航行體水中點火燃氣后效分析與研究?

李智生

（91550部隊 大連 116023）

1 引言

對于采用水中點火的垂直發射航行體而言，通過及時對航行體的水中彈道和姿態進行控制，可提高航行體在水中運動的穩定性，并有助于獲得有利的出水姿態，從而增強航行體出水后的姿態控制能力［1］。通常，水下發射航行體在其尾部離開發射筒口一定距離處點火進行發射。如果航行體尾部與發射筒口距離較近處點火，則發動機可以利用從發射筒內溢出并附著在航行體尾部的燃氣泡，作為發動機噴流建立初期燃氣的受納空間，減輕發動機直接在水中點火所造成的沖擊，提高發動機工作安全性，但是由于水下點火處距離發射平臺較近，發動機高速噴流會對筒蓋及周圍發射平臺結構產生破壞，影響后續發射［2］。如果航行體遠離發射筒口處（簡稱筒口）點火，附著在航行體尾部的燃氣泡體積變小，同時燃氣泡內滲人水，發動機若直接在此環境中點火，由于水的巨大慣性，則發動機噴流會受到水的阻礙，導致噴管內壓強過高，從而威脅發動機工作安全性［3～4］。顯然，在決定采用水中點火方案時，必須明確水中點火對航行體載荷的影響，并充分估計水中點火對發射筒及發射平臺所造成的威脅［5～6］。

本文在構建垂直發射航行體水中點火數值仿真模型的基礎上，研究航行體水中點火過程中尾部流場變化情況，分析不同點火深度下發動機射流流場對發射平臺壁面壓力和溫度的影響，同時對水中點火燃氣后效進行估計。

2 控制方程

建立水下發射過程中的航行體動力模型，通過實時求解航行體受力，通過動力學方程求得加速度和角加速度，然后進行數值積分，獲得航行體當前速度、位移及姿態等。航行體受力如圖1所示，圖1中oxyz為發射坐標系［7］，相對于地球靜止，ox1y1z1為航行體坐標系，固聯于航行體；v為航行體運動速度；F為航行體所受的浮力；G為自身重力；f為航行體軸向阻力；ox1為航行體軸向，ox1與v的夾角為α；oy1與v的夾角為θ，T為發動機產生的總推力；?為發動機噴管為糾正航行體出水姿態而偏轉的擺角。

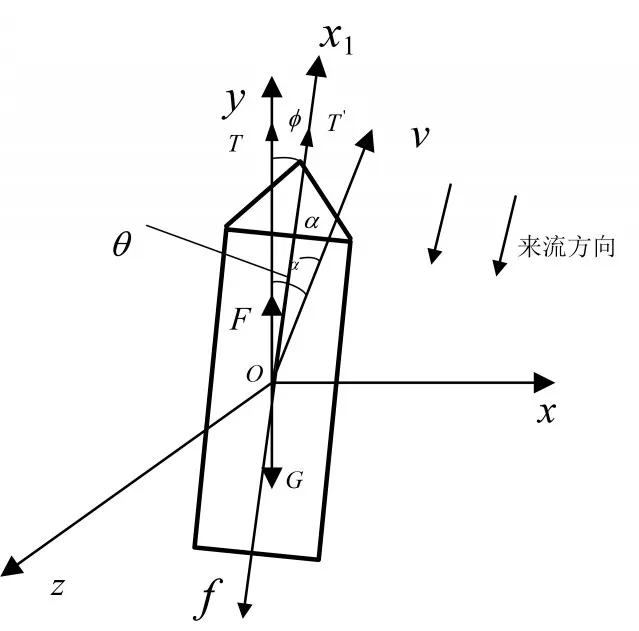
圖1 發射坐標系

航行體在水下發射過程中，首先利用高壓燃氣將航行體彈射出筒，航行體尾部離開發射筒后，筒內燃氣進入外界環境，與周圍的水汽混合并附著在尾部形成燃氣泡。發動機接收到點火指令后，航行體運動的發射動力主要由兩部分組成：彈射力和發動機提供的軸向推力。

航行體在水下發射過程中，其航行體動力模型為［8］

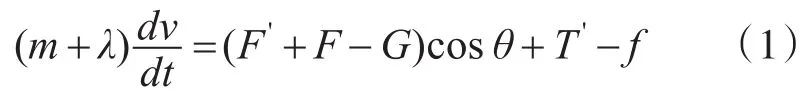
其中：

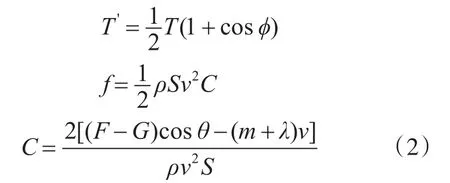
式中：t為航行體運動時間，F'為發射筒高壓燃氣彈射力，T'為發動機點火后航行體受到的軸向推力，m為航行體質量，s為航行體的迎流面積，C為阻力系數，ρ為海水密度，λ為附加質量；α和θ值利用航行體加速度計測量的各個方向的加速度值進行解算求取。式（1）中的航行體運動參數值為后續計算燃氣后效參數提供動態輸入。

3 模型建立

3.1 計算區域及網格劃分

CFD計算模型具體采用二維軸對稱的無限長圓柱體模型。CFD求解器計算域如圖2所示。網格劃分的原則是，全部流場區域采用結構化網格。該方式能夠消除計算結果對網格的依賴性［9～10］。在劃分噴管時，在軸向方向、噴管及尾部附近處的網格大小接近一致。外場劃分梯度網格，靠近航行體位置網格細密，遠場較為稀疏。按照以上要求劃分網格，得到航行體尾部局部網格如圖3所示。

圖2 CFD求解器計算域

圖3 航行體尾部局部網格

將式（1）和式（2）所示的航行體動力模型輸入到CFD求解器中，利用CFD求解器對航行體水下運動參數進行求解。在得到航行體運動參數后對網格節點參數進行更新，進而對航行體能量方程及控制方程進行數值離散求解，最終得出航行體近體流場壓力及溫度分布參數。由于模型的對稱性，計算域模型采取二維軸對稱模型。在建模時不考慮航行體尾部產生的空化現象，且由于研究的是尾部流場變化，頭部對仿真流場的影響較小，因此將計算模型簡化為尾部只有噴管擴張段的無限長圓柱體［11］。

3.2 計算方法

采用Mixture多相流模型對流場進行求解，其控制方程基本形式如下［12］：

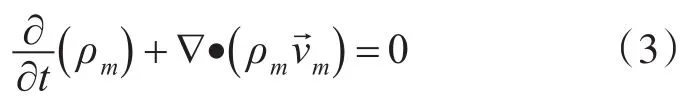
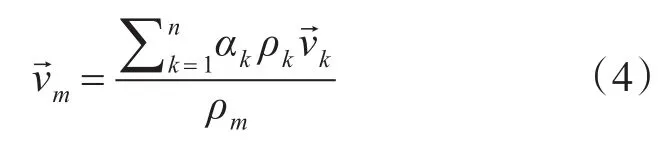
式中，ρm為混合物密度：

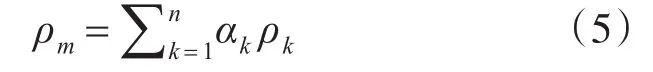
式中，αk為第k相的體積分數。利用Mixture多相流模型進行求解時，分別設置了主相（Primary phase）和副相（Secondary phase），所有相體積分數之和為1，副相可為多個，對于副相p的體積分數求解方法為

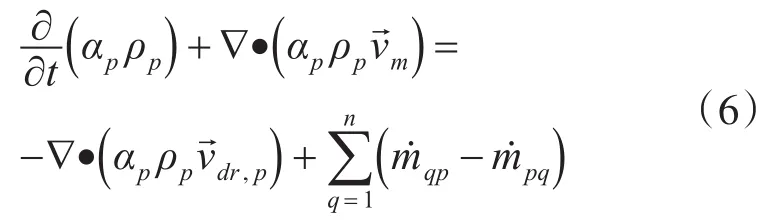
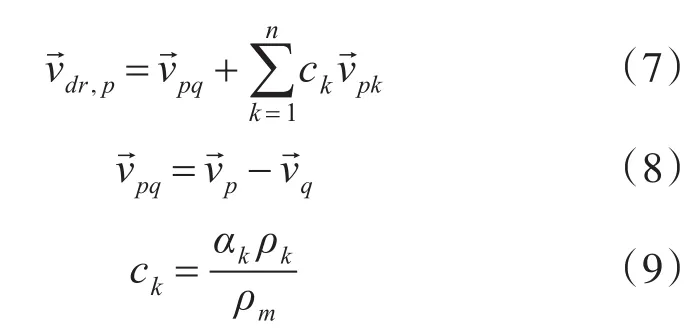
動量方程是牛頓第二定律在流體動力學中的體現。對于Mixture多相流模型的動量方程，可通過將所有相各自的動量方程相加的方法獲得，其表示式為

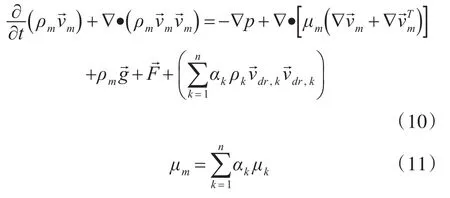
式中，n為相的序號，為體積力，μm為混合物相的粘性，其表達式為

能量方程是能量守恒定律在流體動力學中的體現，Mixture多相流模型中混合物的能量方程為

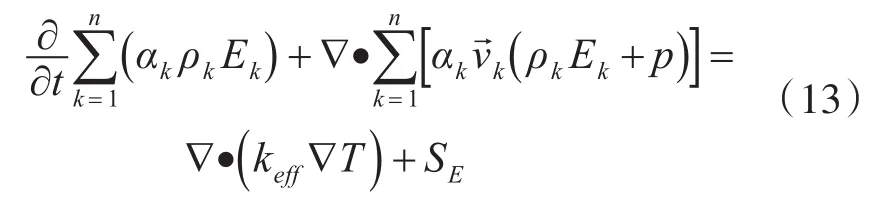
式中，keff為有效傳導系數，表達式為

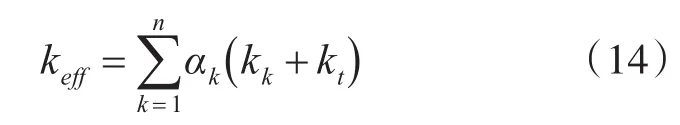
其中，kt為湍動熱傳導系數，kk為第k相的湍動能，其取值取決于所選擇的湍流模型。式（13）右端項中第一項代表了傳導引起的能量遷移，SE為其余的體積熱源項。

對于可壓縮流動，Ek的表達式為

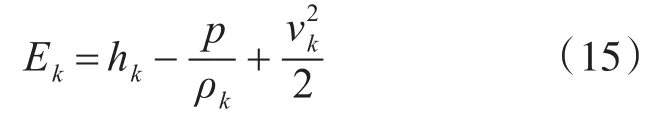
對于不可壓縮流動，表達式為

其中，hk為第k相的焓。

上述偏微分方程組，包括式（3）～式（16），通過網格節點在計算域流場內進行離散化求解，具體步驟如下：

1）在計算過程的每個時間步，利用CFD方法聯合求解Mixture模型控制方程、動量方程、能量方程和航行體動力模型，獲得流場和航行體運動參數，通過更新網格將二者進行耦合，計算完畢后轉入下一時間步；

2）當第一步得到的速度在局部不滿足連續方程時，從連續性方程和線化動量方程推導出壓力校正的泊松方程，然后解出壓力校正方程，獲取壓力和速度場；

3）用上一個時間步長更新的、除了壓力速度和溫度外的其它變量值，解出湍流、能量和輻射等標量；

4）當存在相間耦合時，用離散相軌跡計算來更新連續相的源項；

5）根據計算的殘差曲線檢查設定方程的收斂性，當所有變量的殘差值都降到10-3時，就認為計算收斂，即完成了對壓力和溫度的離散求解。

3.3 計算設置

表1給出了一組計算初始參數設置。

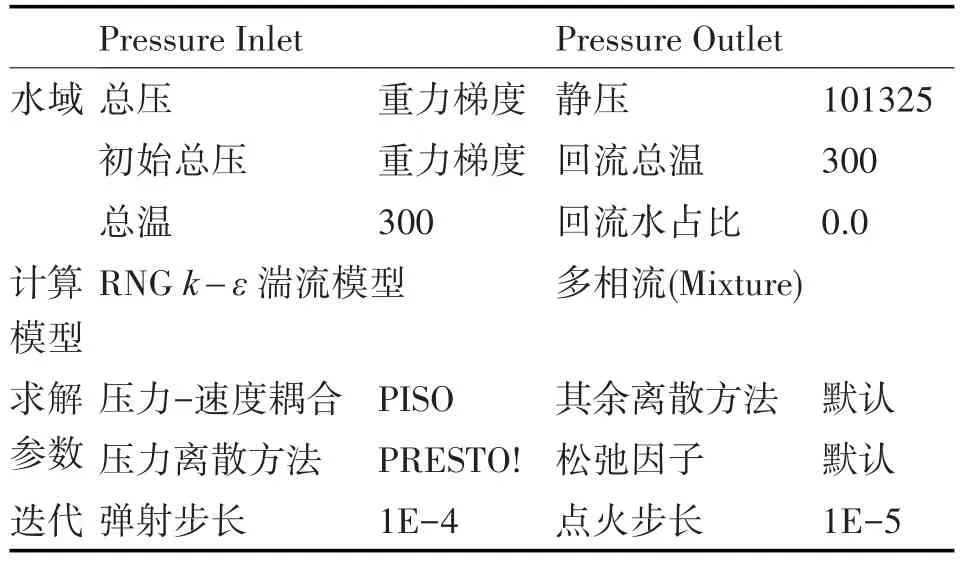
表1 主要參數設置

在水域邊界設置中，初始壓力輸入數值通過重力梯度法獲得。重力梯度法就是根據遠場邊界網格節點坐標和航行體發射水深來計算原場邊界壓力輸入的方法。設標準大氣壓為P0=101325Pa，重力加速度g=9.81m/s2，海水密度ρ=1.02kg/m3，則初始遠場壓力總壓，簡稱為總壓，為P=P0+ρgh，其中，h為壓力邊界網格節點高度與航行體發射深度的差值。總溫及回流總溫初始值由發射筒內溫度傳感器讀取。

在CFD模型設置中，湍流模型采用RNGk-ε，可以達到較好的收斂性；由于流場變量在壁面附近存在很大梯度的流動，因此壁面函數采用非平衡壁面函數法；流場初始化過程中，先對整流場按表1進行參數初始化，而后標記出全部為水的區域并對此區域按表1中初始項給出的參數修正，再迭代計算；在計算步長選擇上，首先保證計算精度，其次要保證單時間步迭代計算的收斂性，最后要考慮計算的經濟性。

在對航行體近體流場進行離散求解后，即可得出流場屬性的關鍵參數（如壓力、密度和溫度等）。

4 仿真計算與結果分析

不同位置點火時，發動機噴管所黏附的燃氣泡體積不同，如果燃氣泡內點火，則可以起到緩沖作用，從而減弱對航行體、發射平臺的沖擊載荷。仿真計算中，通過設置不同的點火距離，分析燃氣后效中壓力和溫度對發射平臺壁面的影響。

采用如表1所示的參數來設置CFD計算模型。假設發動機距筒口點火的距離分別為2.2、4.3、6.5（數值進行了無量綱化處理），對應時間為0.4、0.6、0.8（數值進行了無量綱化處理）。在點火時刻，Fluent設置中將喉部的邊界wall改為壓力入口（PressureInlet），通過Fluent自定義函數（UDF）定義航行體質量和轉動慣量等參數，通過網格節點離散求解航行體水動力及壓力等參數，湍流模型選用增強RNGk-ε模型，計算迭代步長為1E-5。

通過自定義函數UDF設置壓力監測點位置，得到的發射平臺壁面的壓力與溫度的變化規律曲線分別如圖4和圖5所示。從圖4中可以看出，發射平臺壁面各個測點的壓力脈動變化規律基本一致，且離筒口中心越遠，脈動幅值越小，當t>0.7后，壓力值基本維持在當地水深壓力的0.55倍；在點火后，測點Pb1的壓力值出現3次壓力峰值，這是由于Pb1是發射筒與發射平臺壁面的交界點，發動機燃氣射流與發射筒內高壓燃氣同時對Pb1產生作用。圖5所示，發射筒中心處各個測點的溫度變化規律趨于一致，溫度分布符合熱傳導規律，有明顯的滯后，從筒口開始自上而下，溫度降低；在發動機點火發射開始后，測點P1的溫度瞬間升至3000K，其他測點溫度也逐漸升高；其后又出現兩次溫度波動，其峰值要遠低于第一次，期間出現溫度降低的原因是：取兩個典型時刻t=0.231s和t=0.471s，在密度云圖6中這兩個時刻的溫度云圖和流線圖也可以看出，此刻燃氣泡幾乎處于閉合狀態，燃氣溫度無法傳遞。

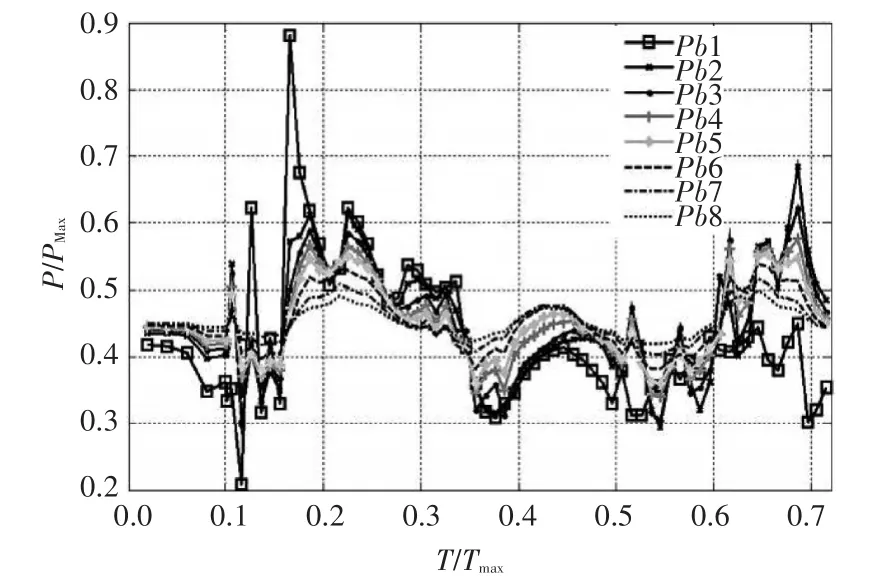
圖4 發射平臺壁面不同測點壓力變化圖

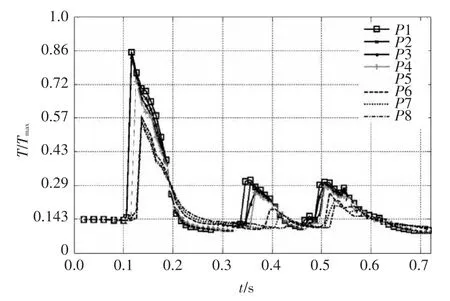
圖5 發射平臺壁面不同測點溫度變化圖

5 結語

本文基于Mixture多相流模型、動網格技術及三維軸對稱模型，建立了航行體水中點火數值仿真模型，仿真計算得到了不同點火深度條件下燃氣后效中壓力和溫度的變化特性數據，結果分析表明，發射平臺壁面各個測點的壓力脈動變化規律基本一致，且離筒口中心越遠，脈動幅值越小；溫度分布符合熱傳導規律，有明顯的滯后，從筒口開始自上而下，溫度降低。研究結論能夠為航行體水中點火時機的選擇提供決策依據，可為發射筒筒口流場分析提供數據支撐。

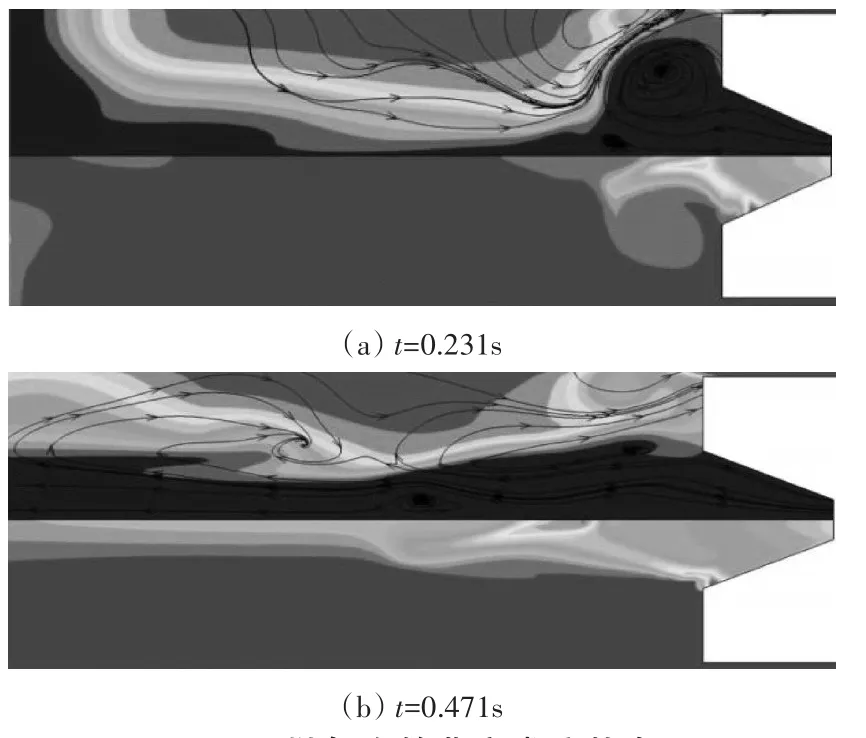
圖6 燃氣泡的非定常流狀態