主動控制狹縫節流氣浮支承結構及承載特性研究*

羅 強 于普良 胡 回 姜 慶 鮮小東

(1.武漢科技大學冶金裝備及控制教育部重點實驗室，機械傳動與制造工程湖北省重點實驗室，省部共建耐火材料與冶金國家重點實驗室 湖北武漢 430081；2.武漢科技大學精密制造研究院 湖北武漢 430081)

靜壓氣浮支承因其具有無摩擦和高運動精度的優點，已經廣泛應用于各種精密設備中，如高精度導軌、光刻機和精密測量儀器等[1-2]。為了提高氣浮支承的承載性能，通常使用的方法是改變氣浮支承結構和采用控制技術。

于普良等[3]研究了不同截面均壓槽對小孔節流氣浮支承承載特性的影響，結果表明，通過增加均壓槽可以提高氣浮支承承載性能。CHEN等[4-5]研究了不同均壓腔結構對小孔節流氣浮支承承載性能的影響。龍威和宗洪鋒[6]研究了環面、狹縫、小孔節流器對空氣靜壓導軌的靜態特性，結果表明狹縫節流效果優于其他2種。控制技術主要有被動控制和主動控制2種。在現有技術中，被動控制技術所提高的承載性能有限。相比之下，由于伺服控制系統的集成，主動控制方法表現出更高的承載性能[7]。ISHIBASHI、HUANG等[8-9]以小孔節流氣浮支承為研究對象，從理論和實驗兩方面證明了主動調節節流面積可以提高支承的穩定性。AGUIRRE、AL-BENDER等[10-11]對氣膜錐度控制進行了改進，利用壓電促動器改變氣膜錐度進而提高了承載性能。朱定玉、吳雙[12-13]通過壓電促動器控制氣膜形狀變化提高了氣浮支承承載性能。MAAMARI等[14]通過線性彈簧控制氣膜的錐度變化，并證明了氣膜的圓錐度越大，產生的承載力越大。

目前許多主動控制的研究都是基于小孔節流方式，以控制氣膜錐度變化為主，而對主動控制狹縫節流氣浮支承的研究較少。本文作者設計了一種主動控制狹縫節流氣浮支承，并建立計算流體動力學模型，通過Fluent仿真研究了徑向狹縫高度變化幅值、徑向狹縫高度、供氣壓力和氣膜厚度對氣浮支承承載性能的影響，為今后主動控制氣浮支承的發展奠定了理論基礎。

1 氣體靜壓支承結構設計

1.1 工作原理

圖1所示為可變節流面積靜壓氣浮支承整體結構示意圖。

如圖1所示，氣體從進氣口進入，通過徑向狹縫通道、軸向狹縫通道、均壓腔流入氣浮支承底部并通過出氣口擴散開，從而起到支承作用。氣浮支承開始工作時，壓電陶瓷促動器受到電壓激勵后輸出動態力，該動態力作用到柔性機構上，在力的作用下做微位移運動，進而導致伸縮機構下端面與氣浮支承下端蓋的上端面之間的徑向狹縫高度Hb改變。徑向狹縫沿中心展開后截面為長方形，氣浮支承節流面積S=2π×D3×Hb，即改變徑向狹縫高度可以改變狹縫節流面積。節流面積的改變直接影響了進入的氣體質量流量，進而達到實現氣浮支承承載力主動控制的目的。運動部分示意圖如圖2所示。

壓電促動器上端與氣浮支承上端蓋螺栓連接，輸出端頂在柔性結構上，伸縮結構與柔性結構螺栓連接，上端蓋、柔性結構、下端蓋三者通過螺栓連接。主要結構參數如表1所示。

表1 氣浮支承主要結構參數

1.2 氣體潤滑數學模型

為了方便對氣浮支承中的流動氣體進行理論分析，建立以下假設條件：

(1)氣體流動過程中流體的狀態變化為等溫過程，即溫度T為常數。

(2)潤滑氣體的黏度系數η恒定。

(3)流體邊界不考慮邊界滑移效應。

(4)潤滑氣體滿足理想氣體狀態方程。

基于以上假設，將N-S方程簡化為一維流動分析，即：

(1)

對y積分2次，可得：

(2)

邊界條件為y=0、z時，u=0，代入式(2)后可得：

(3)

式中：u為流體在x方向的速度；p為狹縫中的壓力分布；μ為氣體黏性系數。

壓電促動器輸出簡諧力作用在柔性結構上，柔性結構在力的作用下做簡諧運動。徑向狹縫實際高度h為

h=hb+Δh

(4)

式中:Δh為擾動高度,

(5)

其中，ω為簡諧運動頻率；t為時間；A為運動幅值。

將式(5)代入到式(4)，此時徑向狹縫氣膜厚度：

h=hb+Δh=hb[1+ε·sin(ωt)]

(6)

綜合徑向狹縫擾動，可得徑向狹縫內質量流量為

(7)

式中:b為徑向狹縫周長；ρ為氣體密度；R為氣體常數；T為絕對溫度。

整理得：

(8)

式中：pa為徑向狹縫出口壓力；h為徑向狹縫高度；f為擾動頻率。

設pb為軸向狹縫出口壓力，pc為氣膜對稱中心壓力。氣膜向內部流動的質量流量為m1，向外流動的流量為m2，且Qm=m1+m2。

(9)

(10)

式中:hf為氣膜厚度；ha為均壓腔高度。將式(9)、(10)積分得到：

這個這個，當然能種。村長極力爭辯。一條尺把寬的溝，充其量占你八斗丘的二十分之一，說不定更少，對你有什么影響呢。

(11)

(12)

式中：p1、p2為對應區間內任意一處壓力，當r=r1時，p1=pb，當r=r2時，p2=p0，對其在區間內積分可得承載力公式：

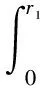
(13)

式中：s為氣浮支承承載面面積。

由公式(8)、(13)可得，承載力與進口質量流量、徑向狹縫高度、變化幅值有關。

1.3 主動控制狹縫節流氣浮支承CFD模型

為研究氣浮支承承載力的動態變化特性，文中利用計算流體力學軟件三維動網格方法，用自定義函數控制徑向狹縫上表面做正弦運動，模擬狹縫高度變化進行瞬態仿真分析。動態工況下狹縫變化如圖3所示。由于空氣靜壓支承的對稱性，文中建立了1/4網格模型，所有網格為六面體網格，狹縫部分進行了網格加密處理。經過仿真驗證，整體網格數量不少于200萬時，計算結果保持穩定。CFD模型圖如圖4所示。

圖5所示為主動控制狹縫節流氣浮支承邊界條件示意圖，進氣口壓力為ps，出氣口壓力為標準大氣壓p0，氣域模型兩側截面為對稱邊界，運動邊界采用UDF控制，采用Dynamic Layering Methods網格更新方法，其他邊界均設置為壁面。計算模型采用k-ε湍流模型，流動介質為理想氣體。

1.4 仿真方法適用性驗證

為了驗證文中氣浮支承CFD模型計算方法的可行性，利用參考文獻[15]中氣浮支承模型，使用文中湍流模型對該氣浮支承進行了分析。文獻[15]中氣浮支承結構示意圖如圖6(a)所示，主要參數包括：氣浮支承半徑R2= 32.5 mm，狹縫深度H=10 mm，氣膜厚度h=3～15 μm，狹縫寬度z=16 μm，狹縫所在圓半徑R1=13 mm。氣體為理想氣體，氣體流動為層流，速度-壓力耦合算法為SIMPLE，供氣壓力ps=0.6 MPa，出口壓力p0=0.1 MPa。

文中模型仿真結果與文獻[15]中實驗與仿真數據對比如圖6(b)所示，3種方法結果具有一致性，驗證了文中仿真方法在氣浮支承計算仿真上的適用性。

2 仿真結果與分析

為研究進氣狹縫節流面積動態變化對氣浮支承承載力的影響，分析徑向狹縫高度變化幅值、供氣壓力、徑向狹縫高度和氣膜厚度對氣浮支承靜態承載力、承載力變化范圍的影響。徑向狹縫高度變化方程為x=Asin(2πft)，f=1 000 Hz，Tp為0.001 s，每個周期迭代步數400步，時間步長為2.5×10-6s。

2.1 不同幅值、供氣壓力對支承承載力的影響

設置氣浮支承CFD模型具體參數為徑向狹縫高度Hb=5 mm，氣膜厚度Hf=10 mm，徑向狹縫高度變化頻率f=1 000 Hz，變化幅值A分別為0.5、1、1.5、2、3 μm，供氣壓力ps分別為0.2、0.3、0.4、0.5、0.6 MPa，其他主要結構參數與表1相同，研究了不同變化幅值、不同供氣壓力時，氣浮支承承載力W隨時間t的變化。

圖7所示為供氣壓力為0.6 MPa，徑向狹縫高度變化幅值為2 μm時，氣浮支承分別在時間t為1/4Tp、1/2Tp、3/4Tp、Tp時刻的壓力云圖。當徑向狹縫處于正弦變化前1/2Tp時，徑向狹縫高度Hb增加，氣體質量流量增加，進而承載力增加，在t=1/4Tp時達到最大值；后1/2Tp時，承載力減小，當t=3/4Tp時，承載力最低。

圖8所示為不同供氣壓力、不同徑向狹縫高度變化幅值對承載力的影響。當供氣壓力ps為0.6 MPa時，隨著徑向狹縫高度變化幅值A的增加，狹縫節流面積S增加，進口質量流量增加，導致氣膜內部壓力分布增強，所以承載力變化范圍逐漸增大。當保證變化幅值A不變時，如A=0.5 μm時，隨著供氣壓力從0.2 MPa增加到0.6 MPa，靜態承載力從220 N增加到310 N左右。可知，在變化幅值一定情況下，靜態承載力和承載力變化范圍隨著壓力的增大而增大；不同幅值時在各壓力條件下，整體承載力變化趨勢相似，呈周期性變化。當0

2.2 不同幅值、徑向狹縫高度對支承承載力的影響

設置氣浮支承CFD模型具體參數為氣膜厚度Hf=10 mm，供氣壓力ps=0.6 MPa，徑向狹縫高度變化頻率f=1 000 Hz，徑向狹縫高度Hb分別為4、5、6、8、10 μm，徑向狹縫高度變化幅值A分別為0.5、1、1.5、2、3 μm，氣浮支承其他主要結構參數與表1相同，研究了氣浮支承底面承載力W隨時間t的變化。

如圖9所示，當徑向高度一定時，隨著狹縫高度變化幅值A的增加，質量流量增大，壓力分布增強，承載力變化范圍逐漸增大。當保證變化幅值A不變時，隨著徑向狹縫高度的增大，靜態承載力增加幅度較小，承載力變化范圍減小。當徑向狹縫高度為10 μm時，隨著時間變化，承載力幾乎不變，范圍最小只有2 N左右。承載力隨時間變化的范圍隨著變化幅值的增大而增大,隨著徑向狹縫高度的增大而減小，變化規律呈周期性變化。在Hb=4 μm，A=3 mm時，承載力最大范圍達到了130 N。

2.3 不同幅值、氣膜厚度對支承承載力的影響

設置CFD模型具體參數為徑向狹縫高度Hb=5 μm，供氣壓力ps=0.6 MPa，徑向狹縫高度運動頻率f=1 000 Hz，氣膜厚度Hf分別為5、10、15、20、25 μm，徑向狹縫高度運動幅值A分別為0.5、1、1.5、2、3 μm，氣浮支承其他主要結構參數與表1相同，研究了不同變化幅值A、不同氣膜厚度Hf時，氣浮支承承載力W隨時間t的變化。

如圖10所示，當氣膜厚度一定時，隨著徑向狹縫變化幅值A的增加，承載力變化范圍同樣增大，承載力均呈周期性變化。當運動幅值不變時，隨著氣膜厚度Hf的減小，靜態承載力和變化范圍都在增大，當氣膜厚度減小到5 μm時，靜態承載力雖然增大但變化范圍縮小。承載力變化范圍隨著運動幅值的增大而增大，隨著氣膜厚度的增大而減小。

3 結論

(1)通過可變節流面積狹縫節流氣浮支承的仿真分析，結果表明主動控制節流面積可以實現氣浮支承承載力的動態調節，為主動控制氣浮支承的研究奠定了理論基礎。

(2)當主動控制節流面積氣浮支承的其他參數不變時，保持徑向狹縫高度變化幅值一定，增大供氣壓力，靜態承載力及變化范圍都大幅度增加；供氣壓力一定時，承載力變化范圍隨著變化幅值的增大而增大。

(3)當主動控制節流面積氣浮支承的其他參數不變時，保持徑向狹縫高度變化幅值一定，增大徑向狹縫高度，靜態承載力增加，但變化范圍減小；徑向狹縫高度一定時，承載力變化范圍同樣隨著變化幅值的增大而增大。

(4)當主動控制節流面積氣浮支承的其他參數不變時，保持徑向狹縫高度變化幅值一定，增大氣膜厚度，靜態承載力大幅度降低，但變化范圍先增大后減小;氣膜厚度一定時，承載力變化范圍同樣隨著變化幅值的增大而增大。