條混工藝參數對混合效果的影響
曹巧麗, 李 豪, 錢麗莉, 郁崇文,2
(1. 東華大學 紡織學院, 上海 201620; 2. 東華大學 紡織面料技術教育部重點實驗室, 上海 201620)
多種纖維混紡能夠利用各組分纖維的不同性能實現優勢互補,獲得較好的成本效益,因而被廣泛應用[1]。混紡紗生產時,主要是通過條混(并條混合)和散纖維混合2種方式進行纖維混合[2]。因條混混紡比容易控制,對纖維品種適應性強,應用更為廣泛[3]。多組分纖維在紗條內的混合均勻程度決定了紗的強度、外觀等質量[4-6],因此,紗條中纖維分布的均勻性是影響混紡紗性能的關鍵。
目前通常采用漢密爾頓指數(MI)[7]和混合不勻指數(IBI)[8-10]對混紡紗的混合均勻程度進行表征。MI通過計算紗條截面上各層圓環內纖維根數的變化來描述纖維在紗條的內外層(芯層和表面)的分布和轉移情況,但是無法表征纖維在紗條截面的周向上的分布情況,此外,沿紗條長度上的混合情況也無法表征。也有學者以實際混合不勻率與理論混合不勻率的比值作為量化混合均勻程度的指標。一般認為紡紗過程中纖維的混合是“隨機過程”,此隨機混合能夠達到的最佳混合程度被認為是理論混合均勻度。還有學者[11-15]假設兩組分纖維在紗條內服從二項分布并且“完全隨機混合”,建立了在紗條長度片段上纖維理論混合不勻公式。在實際測量混紡紗條內纖維的混合均勻度方面,有研究是以紗條長度片段間的混紡比變異系數或偏差作為實際混合不勻率[13,16-17],但是此IBI指數只能表征在紗條片段長度上混合的情況,對于紗條截面上,包括周向和徑向的混合情況無法說明。
條混時纖維受到的牽伸與集束作用使其產生運動并在紗條內重新排列,決定了最終纖維在紗條內的分布與混合。不同的工藝參數下纖維運動不同,導致混合均勻程度不同。文獻[18-20]通過實驗將色紡紗進行切片成像對比分析,定性地探究了混合方式、混紡比等參數對MI的影響,但是由于MI的局限性,導致其無法表征混合均勻度。目前對其他條混參數對纖維混合影響的系統研究鮮見報道。由于纖維細長柔軟,其混合過程較粉體等顆粒物的混合過程更為困難,僅采用實驗的方法不僅耗時耗力,也無法準確獲得紗條中纖維的分布和混合情況。采用計算機可模擬纖維在牽伸過程中的運動,預測紗條條干均勻度[21-24];同時在模擬纖維條混時的運動方面已取得一定的進展,并實驗驗證了其可行性[25],為探究不同工藝對條混效果的影響提供了參考。
為進一步探究條混工藝參數對紗條內纖維混合均勻度的影響,本文改進了混合不勻指數IBI的計算方法,用包含纖維在紗條截面(徑向與周向)和縱向混合均勻程度的IBI來更全面、綜合地表征纖維在紗條中的混合效果。采用計算機模擬不同工藝參數下的條混過程,結合實驗驗證,揭示出混紡比、并條道數、并合根數、牽伸倍數、羅拉隔距等工藝參數對各組分纖維在紗條中混合均勻度的影響規律。
1 混合不勻指數

在前人的研究中可以看出,在紗條混合不勻率測量以及理論混合不勻率計算時,僅針對紗條的長度片段混合,無法表征紗條內部的混合情況,因此,本文在考慮紗條長度上的混合情況的同時,綜合考慮紗條在截面上,尤其是徑向與周向上的混合與分布情況,達到綜合表征紗條內纖維整體混合均勻度的目的。
1.1 理論混合不勻率
基于前人的研究[14],把混紡紗條看作是纖維在其內部隨機排列的理想紗條,且不同組分纖維完全隨機混合,因此對混合紗條中纖維的理論混合不勻的推導基于以下假設[14]:1)在紗條截面上,纖維根數的分布服從泊松分布;2)紗條截面為圓形,且纖維在該截面上的位置服從均勻分布;3)纖維沿紗條軸向伸直且平行,如圖1所示。

圖1 紗條中纖維分布示意圖
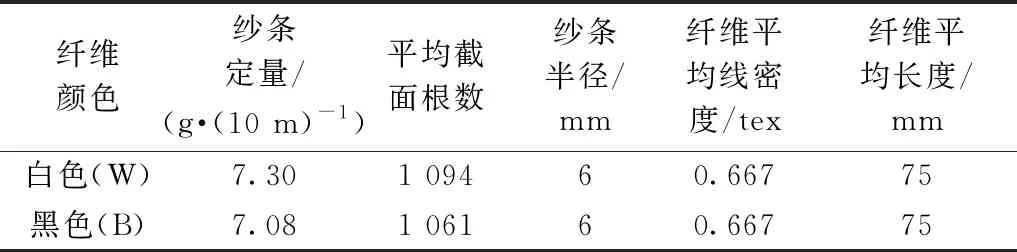
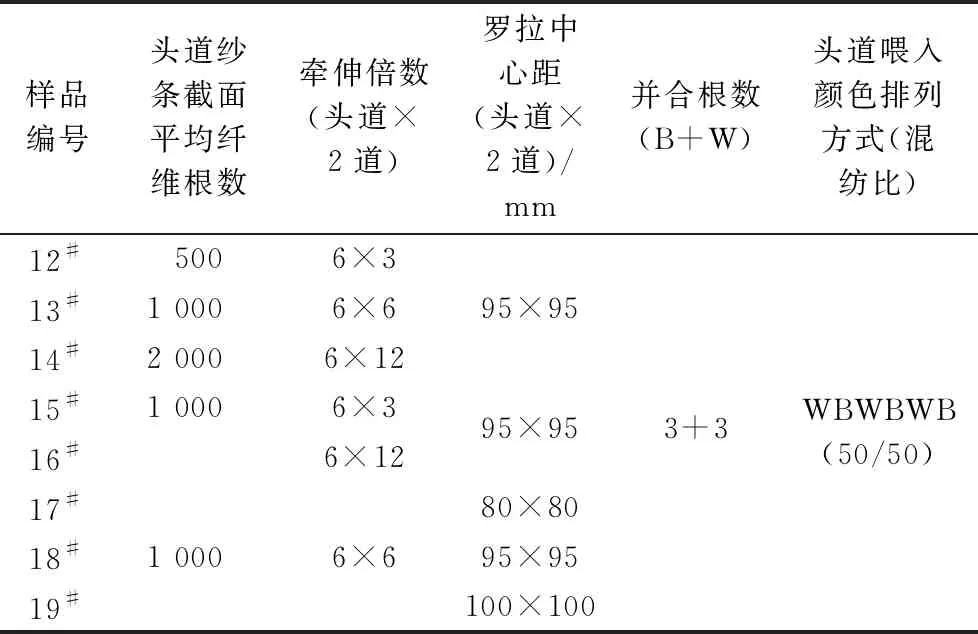
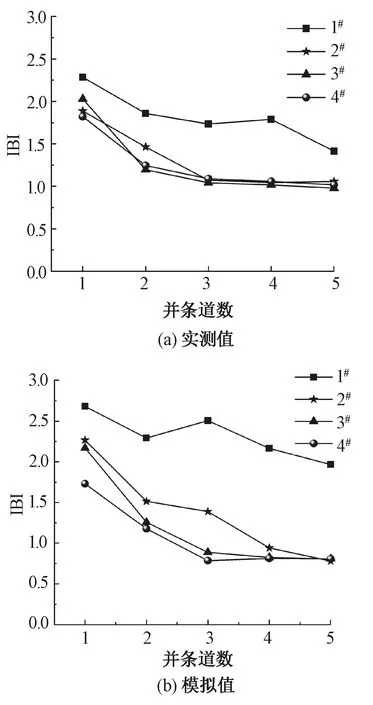
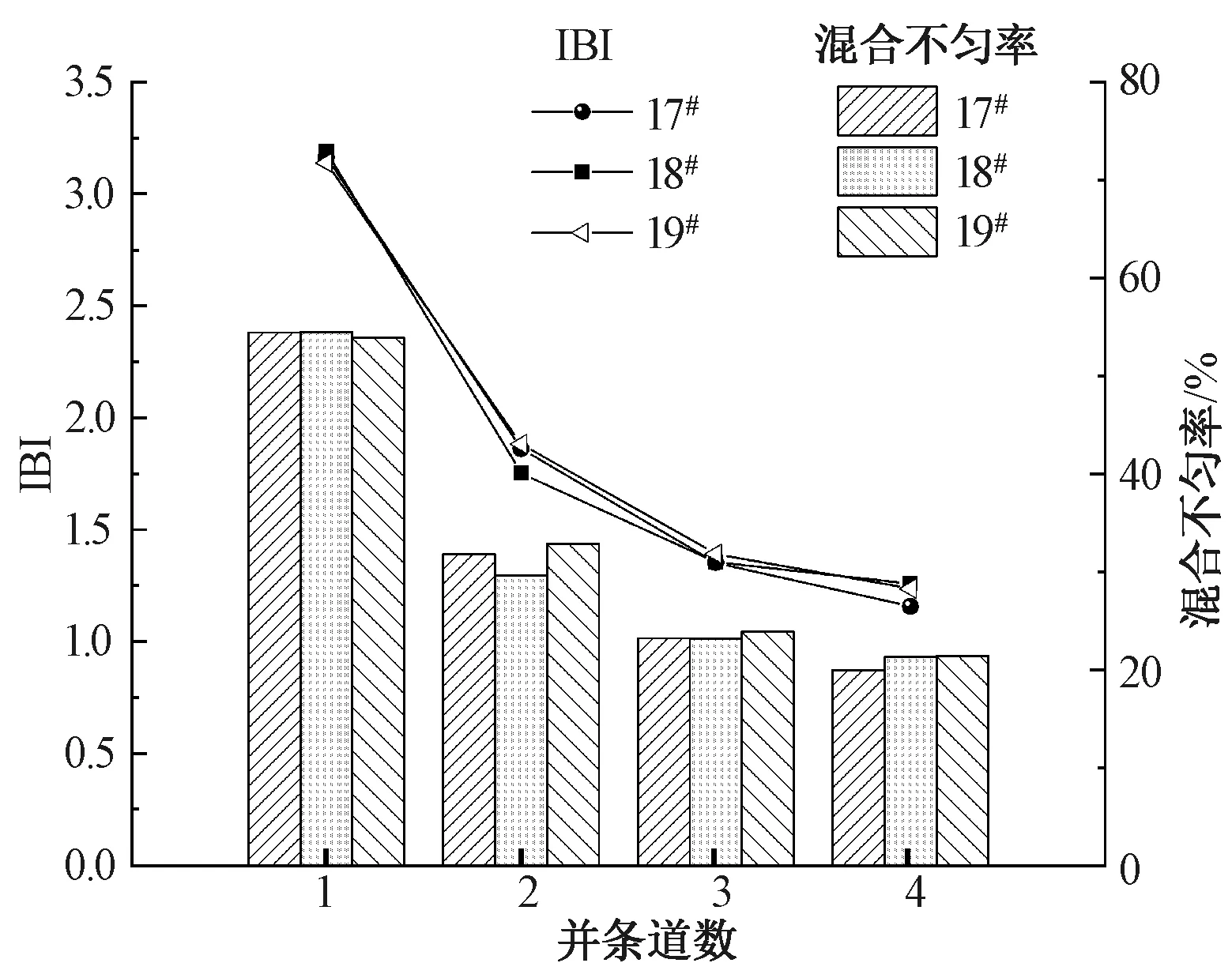
為表征紗條截面上的混合分布情況,在紗條截面上沿周向和徑向,將紗條截面劃分成s個扇形環,如圖1(a)所示。同時沿紗條縱向將紗條劃分成長度相等的片段,如圖1(b)所示。根據假設1),紗條截面平均纖維根數N服從參數為λ的泊松分布,即N~π(λ)。根據假設2),A、B兩種組分纖維混紡,在紗條截面上A纖維的根數為X,其混紡比例為p,纖維B的纖維根數混紡比例為q,p+q=1,且定義p (1) (2) 采用前期研究[11-13]提出的混合不勻率的測試方法,將紗條按照圖1所示的方式進行劃分,分別測量每個扇環單元內的A組分纖維的混紡百分比(對于兩組分混紡,A組分混紡比小于B組分),然后代入式(2)[11,15,25],可計算實際混合不勻率Cm。 (3) 混合不勻率指數IBI為實測混合比不勻率與理論混合比不勻率的比值[12]: (4) 一般來說,IBI>1,且IBI越接近1,表明纖維的混合效果越接近完全隨機混合狀態。如若在紡紗過程中對纖維的運動以及混合加強干預,使其各個組分的纖維達到有規則的間隔排列,則IBI可望小于1,此時纖維的混合效果比理論上完全隨機混合的效果更好。 2.1.1 實驗原料 黑、白2種顏色的滌綸均取自上海德福倫化纖有限公司,分別依次經過梳理、并條后制得2種顏色的紗條。紗條及纖維參數如表1所示。 表1 纖維與紗條性能參數 2.1.2 條混實驗 為驗證模擬的準確性,并進一步探究并合根數、并條道數、混紡比等工藝參數對混合均勻度的影響,采取以下實驗方案進行驗證,如表2所示。 表2 條混實驗方案 2.1.3 混合條截面制樣 將每道條混后的混合條用哈氏切片器切片制樣,并在顯微鏡下采集截面圖像如圖2(a)所示。每組5張圖像,以計算其混合不勻。 圖2 混合紗條截面圖像 2.1.4 混合不勻指數IBI計算 采用計算機圖像處理技術提取紗條截面圖像,并計算其中心點,將紗條截面分割為6×10個面積相等的扇環,如圖2(b)所示。由于實驗所用纖維原料為等長度、等線密度的滌綸纖維,因此其單元格中的纖維根數比即為混紡比。依次計數每組的5張紗條截面圖中各個單元內的白色與黑色纖維根數,算出混紡比,根據式(1)~(3)計算得到混合不勻指數。 采用本文課題組前期模擬條混過程的方法,模擬纖維在條混時的運動過程,得到并條混合后的紗條中纖維的分布情況,以此來預測各組分紗條在并條中的混合效果。模擬過程[25]主要分為以下幾步: 1)根據纖維長度、線密度、紗條定量以及混紡比等參數生成三維立體的紗條,對每根纖維頭尾端坐標進行賦值。 2)根據紗條在牽伸區中變速點分布、羅拉轉速、牽伸倍數、羅拉隔距等工藝參數,計算每根纖維開始變速的時間以及總位移。 3)根據紗條中纖維在前羅拉輸出集束區的位置和速度,計算纖維經過集束后纖維的頭尾端坐標。 4)根據集束后紗條內纖維的分布,按照圖1劃分的方式,在紗條截面上劃分為60個面積相等的扇環,在紗條縱向上劃分100個長度相等的片段,依次計算每個扇環內的混紡比,代入式(2)計算混合紗條的實際混合不勻率。然后按照式(1)和式(3)計算IBI。 5)將混合后的紗條沿其紗軸隨機旋轉某一角度,并將此旋轉后的紗條按照所需的并合數排列喂入下一道并條混合,重復步驟2)、3)、4),可以得到多道并條混合后的紗條。 為了探究紗條定量、牽伸倍數以及羅拉隔距等工藝參數對混合效果的影響,采用表3中的實驗參數進行模擬,其中以紗條截面中平均纖維根數作為輸入參數來表征紗條定量。 表3 模擬計算方案 對表2中的1#~4#樣品進行實驗,以探究不同并合根數對條混效果的影響。采用混合不勻率[25]以及本文改進的IBI分別表征紗條的混合效果。1~5 道條混后紗條的實際混合不勻率如圖3(a)所示,混合不勻指數IBI如圖4(a)所示。將實驗中的纖維、紗條參數以及對應的條混工藝參數輸入模擬程序,得到混合紗條內纖維的分布,并計算出模擬的混合不勻率與IBI,如圖3(b)、圖4(b)所示。 圖3 并合根數與混合不勻率的關系 圖4 并合根數與IBI的關系 由于混紡比相同,紗條截面中各組分纖維的根數相近,因此混合不勻率與IBI計算結果趨勢一致。由圖3、4可以看出,模擬結果與實測結果趨勢一致,由于1#樣品實驗中并合(混合)根數少(只有2根條子),因此,其混合效果最差,1#樣品的IBI指數比2#、3#、4#樣品均高50%以上。隨著并條道數的增加,IBI逐漸下降,在3~5道并條時,2#、3#、4#樣品的IBI逐漸減小并趨于1。并合根數越多,越能在較少的并條道數下達到較低的IBI值。因為并條道數的增加相當于并合根數指數級增加,其并合(混合)的效果越強。因此,增加并合根數、提高并條道數在一定程度上是提高混合效果的簡便、有效手段。但是并條道數過多會導致纖維過度牽伸,從而造成損傷,因此提高混合效果,應先增大并條根數,再考慮增大并條道數。 對表2中4#~6#樣品進行實驗,以分析在相同的混紡比和并合根數下,頭并時喂入條排列方式對條混效果的影響。實測與模擬的混合不勻率、IBI結果如圖5、6所示。 圖5 頭道并條喂入排列方式與混合不勻率的關系 由圖5和圖6可以看出,在相同的混紡比和紗條線密度下,混合不勻率與IBI結果一致。對比4#、5#、6#3種不同頭并排列方式可以看出,4#樣品即2種紗條一根隔一根地間隔排列的IBI較小,5#樣品即每2根間隔排列的IBI次之,6#樣品即4根黑色4根白色分開排列的IBI最大。隨著并條道數的增加,混合不勻率與IBI逐漸降低,且3種排列方式的混合效果逐漸接近,尤其是在3道并條以后,3種排列方式下的混合紗條的混合不勻率與IBI均逐漸接近一致。說明增加并條道數,可以有效降低因排列方式導致的混合不勻的問題。4#試樣能夠在更少的并條道數下達到更小的混合不勻率,表明在條混時,將不同品種的紗條盡可能間隔排列,能夠減少并條道數,并提高混合效果。 圖6 頭道并條喂入排列方式與IBI指數的關系 對表2的4#、7#~11#樣品進行實驗,以分析混紡比對條混效果的影響。實測與模擬的混合不勻率、IBI指數結果如圖7、8所示。 圖7 混紡比與混合不勻率的關系 由圖7可以看出,隨著并條道數的增加,混合不勻率逐漸下降,實測值與模擬值有相同的趨勢。此外,混紡比越小,混合不勻率越大。但是由于混紡比不同,混合不勻率無法直接表征在不同混紡比下的條混效果,因此需要比較IBI。從圖8(a)可以看出,隨著并條道數的增加,IBI降低速率逐漸減緩并處于波動的狀態,而不像圖8(b)那么平穩,這可能是由于實際紗條本身的條干不勻造成的。從整體上看,兩組分混合時,混紡比越接近50/50,IBI指數越小,越易混合均勻。 圖8 混紡比與IBI指數的關系 對表3中12#~16#樣品進行模擬,模擬了不同定量的2種紗條經過2道不同牽伸倍數的條混,計算其混合不勻率和IBI,模擬結果如圖9所示。 圖9 牽伸倍數、紗條定量與混合不勻率以及IBI指數的關系 從圖9(a)可以看出,12#、13#、14#樣品在2道并條混合時牽伸倍數不同,但是其輸出定量相同時,其混合不勻率、IBI均接近。說明牽伸倍數對條混效果沒有顯著影響。由圖9(b)可以看出,紗條定量越大,混合不勻率越小,而不勻指數增大,而實際經驗也顯示定量越大,越難混合均勻。這說明了混合不勻率無法準確表征不同定量的紗條混合均勻度,而混合不勻指數則可以較好地評述不同定量紗條的混合均勻程度。 對表3中17#、18#、19#樣品進行參數模擬,模擬了相同定量的2種紗條經過2道不同羅拉隔距的條混,計算其混合不勻率和IBI指數,模擬結果如圖10所示。 圖10 羅拉中心距與混合不勻率以及IBI指數的關系 由圖10可以看出,羅拉隔距不同,各道并條后IBI指數與混合不勻率均接近,說明羅拉隔距對條混的混合均勻度沒有明顯的影響。 為揭示條混時影響纖維在條子中混合均勻程度的因素,本文采用計算機模擬與實驗相結合的方法探究了條混工藝參數對混合均勻程度的影響,并采用改進的、綜合考慮了纖維在紗條縱向和截面(徑向及周向)的混合不勻指數IBI來表征混合均勻程度。研究結果表明,該IBI能更準確表征混紡紗條的混合均勻程度;增大并條道數、提高并合根數能夠有效降低混合不勻指數;各組分喂入排列越均勻,兩組分混合時各混紡比越接近50/50,紗條定量越小,越易混合均勻;牽伸倍數與羅拉隔距對條混效果沒有明顯影響。上述的計算機模擬結果與實測結果具有一致性,可以用于預測條混后紗條的混合均勻程度。 -------------------- 致謝感謝上海市現代紡織前沿科學研究基地對本文的資助。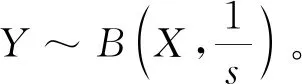

1.2 實際混合不勻率

1.3 混合不勻率指數測試
2 條混實驗與模擬
2.1 實驗部分


2.2 條混模擬
3 結果與討論
3.1 并條道數與并合根數

3.2 頭道并條排列方式


3.3 混紡比


3.4 牽伸倍數與紗條定量

3.5 羅拉中心距
4 結 論

