基于壓縮感知理論的大規模MIMO 系統下行信道估計中的導頻優化理論分析與算法設計
曹海燕 葉震宇
(杭州電子科技大學,杭州 310018)
針對大規模多輸入多輸出(multiple input multiple output,MIMO)系統信道估計中的導頻設計問題,在壓縮感知理論框架下,提出了一種基于信道重構錯誤率最小化的自適應自相關矩陣縮減參數導頻優化算法.首先以信道重構錯誤率最小化為目標,推導了正交匹配追蹤(orthogonal matching pursuit,OMP)算法下信道重構錯誤率與導頻矩陣列相關性之間的關系,并得出優化導頻矩陣的兩點準則,即導頻矩陣列相關性期望和方差最小化;然后研究了優化導頻矩陣的方法,并提出相應的自適應自相關矩陣縮減參數導頻矩陣優化算法,即在每次迭代過程中,以待優化矩陣平均列相關程度是否減小作為判斷條件,調整自相關矩陣縮減參數值,使參數不斷趨近于理論最優.仿真結果表明,與采用Gaussian 矩陣、Elad 方法、低冪平均列相關方法得到的導頻矩陣相比,本文所提方法具有更好的列相關性,且具有更低的信道重構錯誤率.
1 引言
傳統的下行信道估計方法,如最小二乘(least square,LS)信道估計和最小均方誤差(minimized mean square error,MMSE)信道估計[1],需要根據基站端天線數目的增加線性增加導頻數目,具有很高的導頻開銷和計算復雜度.基于壓縮感知[2](compressed sensing,CS)的信道估計方法利用大規模多輸入多輸出(multiple input multiple output,MIMO)無線信道在波束域或時延域信道參數中大部分元素接近于零[3],少部分元素包含了信道的絕大部分能量的特征,將信道抽象為稀疏模型,通過很少的測量次數恢復整個信道.有效降低信道估計中的導頻開銷.壓縮感知信道估計的兩個關鍵問題是感知矩陣的選擇和信道恢復算法,如何設計合適的感知矩陣以及高效的信道恢復算法對提高信道估計的精確性及降低復雜度有重要意義.因此這也成為大規模MIMO 信道估計中的重點問題.
目前Elad[4]、Xu 等[5]和Abolghasemi 等[6]報道了典型的感知矩陣構造方法.這些方法均通過縮減感知矩陣列相關性,達到提高信號重構性能的目的,但缺少對感知矩陣列相關性與信號重構錯誤率之間關系的理論分析.Elad[4]首次通過逐步迭代縮減由感知矩陣構造的Gram 矩陣中的非對角線元素使感知矩陣平均列相關性逐步減小,最后得到優化的感知矩陣,該算法構造的感知矩陣重構錯誤率較低,但矩陣縮減參數的選擇缺少理論依據,不當的矩陣縮減參數可能導致算法的重構性能下降.Xu等[5]和Abolghasemi 等[6]的算法采用等角緊框架(equiangular tight frame,ETF)[7],將感知矩陣逐步逼近EFT,其重構錯誤率比Elad[4]進一步降低.文獻[8]同樣依據ETF,將矩陣縮減參數直接取值為ETF 下界,并考慮了低冪平均列相關性的感知矩陣相關性定義,獲得了相關性更好的感知矩陣,但在實際中,ETF 下界是無法達到的,其并不一定是最優的矩陣縮減參數,且該算法采用固定的迭代次數,無法判斷優化過程是否收斂,存在優化性能不足或浪費計算資源的問題.針對以上問題,本文提出了自適應自相關矩陣縮減參數導頻優化算法.
首先將大規模MIMO 信道恢復問題抽象為稀疏信號恢復問題,給出了兩種導頻矩陣互相關性定義.并以信道重構錯誤率最小化為目標,根據正交匹配追蹤(orthogonal matching pursuit,OMP)算法分析導頻矩陣列相關性與信道重構錯誤率之間的關系,得出優化導頻矩陣的兩點準則:導頻矩陣列相關性期望最小化和方差最小化.然后研究優化導頻矩陣的方法,推導出導頻自相關矩陣縮減參數的最優下界和待優化導頻矩陣平均列相關程度的表達式,定義了相應的自相關矩陣縮減參數,并提出自適應自相關矩陣縮減參數導頻優化算法,即在每次迭代中,通過判斷優化矩陣平均列相關程度是否減小,調整自相關矩陣縮減參數值不斷靠近理論最優,且在內層循環通過計算導頻自相關矩陣與縮減自相關矩陣的差值范數的變化情況來判斷優化是否正在進行,保證算法收斂.最后設定仿真性能分析標準并給出仿真結果.仿真結果表明,相較于隨機Gaussian 矩陣[9]、Elad[4]方法和低冪平均列相關方法,采用所提出的導頻優化算法得到的導頻矩陣具有更優的矩陣列相關性,且可達到更低的信道重構錯誤率.
下文所用符號定義如下:E(·),D(·)和〈·〉分別表示取期望值,取方差值和求內積;xij,xi和hj分別表示矩陣的第i行j列的元素,第i列和信道向量h的第j個分量;代表集合 Ω 的補集.
2 系統模型與OMP 算法介紹
2.1 大規模MIMO 系統模型
本文采用一般的頻分雙工(frequency division duplex,FDD)大規模MIMO 系統模型,如圖1 所示.
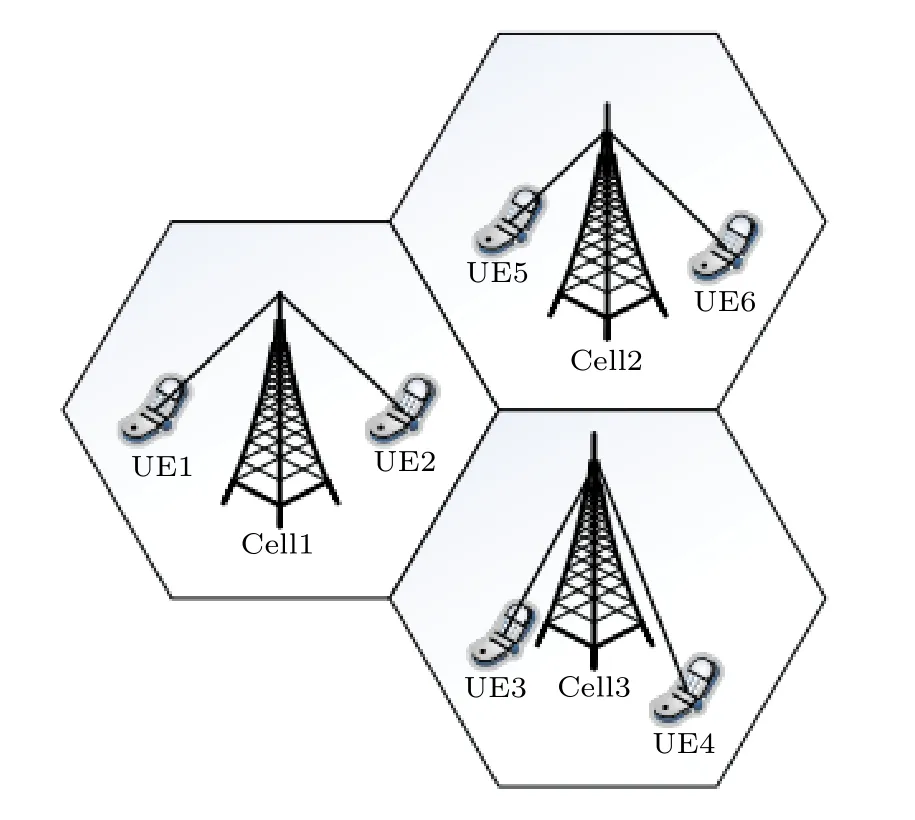
圖1 FDD 大規模MIMO 系統模型Fig.1.The FDD large-scale MIMO system model.
考慮一個基站端配置N根天線,分布U個單天線用戶的MIMO 系統,假設基站端共發送M次導頻序列,則對于每個單用戶,頻域接收信號y∈RM可表示為

其中,X ∈RM×N和h ∈RN分別為頻域導頻矩陣和頻域信道向量.理論研究表明,信道向量在角度域表現出稀疏性[1],即,F為離散傅里葉變換(discrete Fourier transform,DFT)矩陣[10],表示為

為角度域的稀疏信道向量,同樣將導頻矩陣在角度域中表示為為角度域信道矩陣,則 (1)式可改寫為
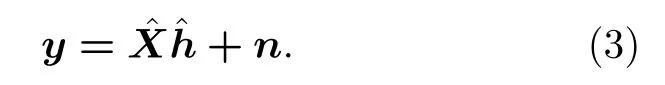
2.2 壓縮感知理論模型
壓縮感知[11]本質上是一個逆線性問題,目的是從少量的線性測量值中恢復高維的信號.
設信號x ∈RN存在稀疏變換Ψs,s ∈RN為稀疏向量,即‖s‖0=D,D ?N,Ψ ∈RN×N為字典矩陣,可以通過測量矩陣Φ ∈RM×N(M ?N)獲得測量值y ∈RM,則y=Φx=ΦΨs=Θs,其中Θ=ΦΨ為感知矩陣,當感知矩陣Θ滿足2K階約束等距性質(restricted isometry property,RIP)時,可采用l0范數最小化方法對稀疏信號進行重構,即
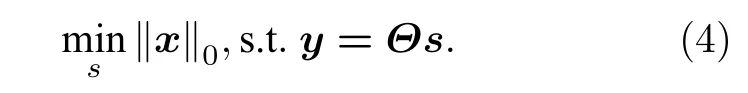
若考慮存在少量有界噪聲的情況,即y=Θs+n,則(4)式可改寫為
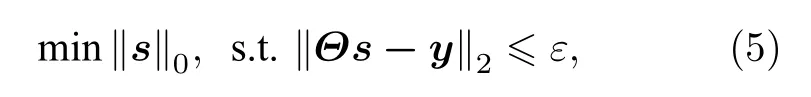
其中,ε為噪聲功率的界值.(4)式和(5)式均可以通過OMP 算法求出近似解[12].
2.3 導頻矩陣互相關性定義
由2.1 節和2.2 節分析可知,信道估計中導頻矩陣的設計問題就是壓縮感知中感知矩陣的設計問題.在信道估計中,導頻矩陣X的自相關矩陣為R=XTX,可根據選取R中非對角元素最大值,將一般的導頻矩陣列相關性定義為
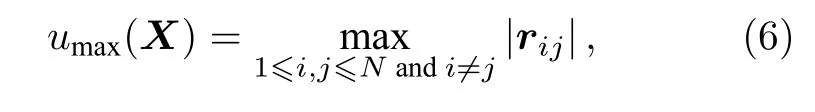
(6)式僅考慮了X中相關性最大的列,沒有考慮其余可能存在的相關性較大的列,缺少對矩陣相關性全面的評價,可以考慮更為全面的定義[8],
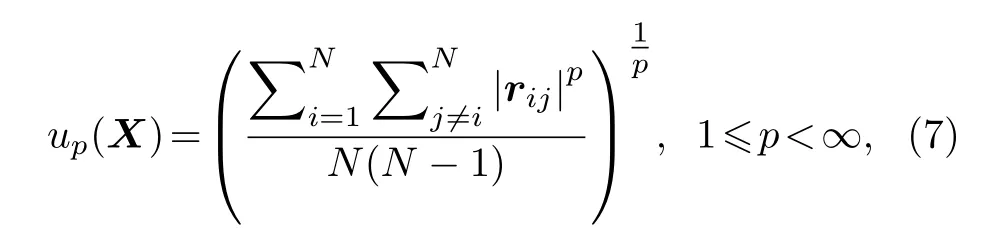
通過調整參數p的值,可以改變up(X) 判別列相關性中數值大的元素多少的能力.當p →∞時,(7)式即為定義(6)式.
2.4 OMP 信道估計算法介紹
OMP 算法是一種基于迭代的貪婪算法,把信號看成是感知矩陣的列向量通過線性組合構成,給定一個信號y,尋求通過感知矩陣列向量的稀疏線性組合來表示信號y.
考慮MIMO 信道估計模型為
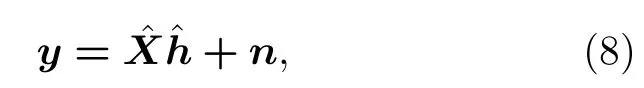
假設信道稀疏度為K,即信道向量只有K個非零分量值,其余分量值等于或接近于零,信道分量指標集合Ω={1,2,···,N},信道非零分量指標集合Ωi={i(1),i(2),···,i(K)}?Ω.
OMP 算法本質上尋找的目標是Ωi.假設在OMP 算法第m次迭代后,已選擇出m個非零信道分量指標Ω(m)={i(1),i(2),···,i(m)},對應的導頻子矩陣X(m)=[xi(1),xi(2),···,xi(m)].則信道估計值(m)∈RN,接收信號估計值(m)∈RM和殘差r(m)∈RM分別計算為[13]
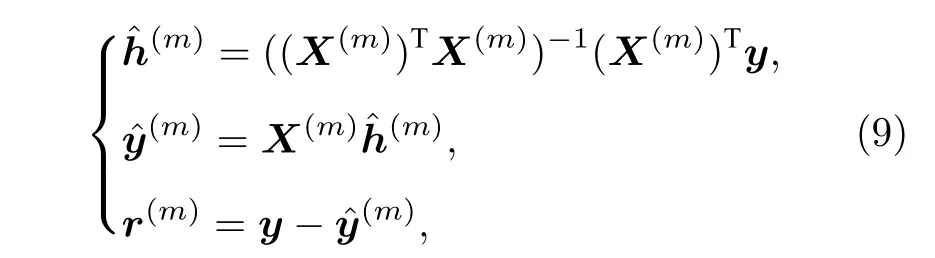
殘差r為原始信號y與導頻矩陣列向量的線性組合的差值,它描述了還沒有被解釋的測量值.
在第m+1 次迭代,OMP 算法的相關性計算為
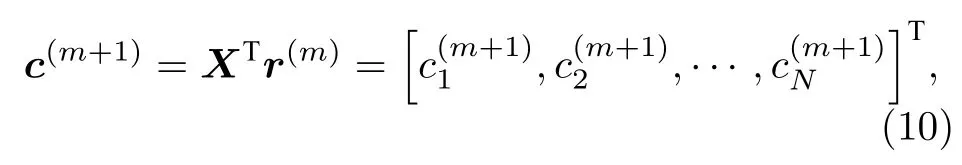
其中c(m+1)∈RN為相關性數值向量.OMP 算法每次尋找相關性數值最大的指標i(m+1)=,j=1,2,···,N,并將對應的導頻列向量加入到原來的導頻子矩陣,生成新的導頻子矩陣,最后通過最小二乘法恢復信道向量,
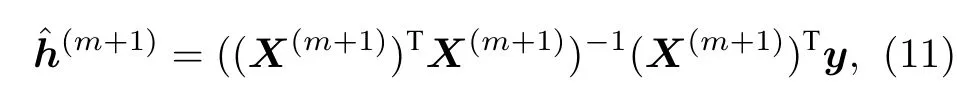
經過K次迭代后,(K) 即為OMP 算法最終得到的信道向量估計值.
3 OMP 算法下導頻矩陣優化準則及一般稀疏算法下的推廣
3.1 OMP 算法信道重構錯誤率與相關性判決的關系
OMP 算法的目的是通過相關性判決尋找信道中非零元素的位置,在算法每一次迭代中,相關性判決越容易找到信道元素值較大的位置,則信道重構越準確,信道重構錯誤率越小.
設導頻矩陣為隨機矩陣,各列均歸一化且任意兩列相關性取值〈xi,xj〉=αi,j,i,j ∈Ω,當i=j時,αi,j=1.
假設在OMP 算法第m+1 迭代中,信道向量h任意兩分量指標l,s ∈Ω,l/=s且|hl|>|hs|,指標l,s對應的相關性數值分別為.顯然是與αi,j,i,j∈Ω相關的隨機變量.它們絕對值之差的期望值體現了相關性判決正確與否的整體趨勢,則相關性判決期望值取值正確的條件為
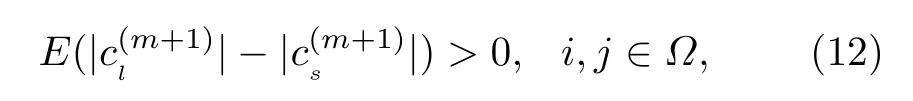
其中,E(·) 代表取期望值.
為了最小化OMP 信道重構錯誤率,在OMP算法每一次迭代中,目標函數為
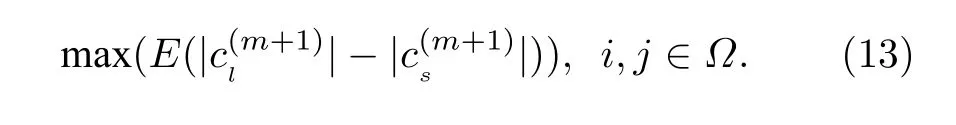
3.2 OMP 算法下導頻矩陣優化準則
定理1使OMP 信道恢復算法重構錯誤率最小化的導頻矩陣優化準則為
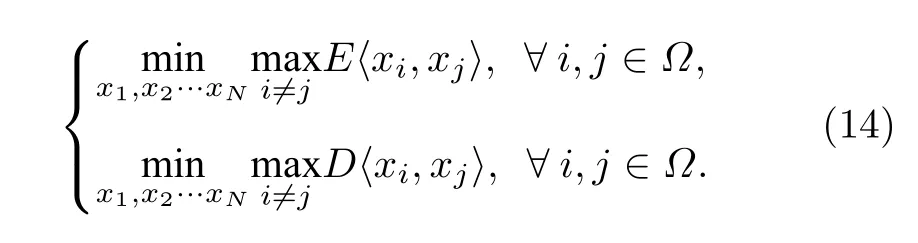
證明詳見附錄A.定理1 說明使OMP 信道恢復算法重構錯誤率最小化的準則為:導頻矩陣列相關性期望絕對值的最大值和方差的最大值最小化.它表明了導頻矩陣列相關性期望的取值越集中,且越接近于零時,OMP 算法的信道恢復性能會越好.
3.3 導頻矩陣優化準則在一般稀疏恢復算法下的推廣
根據壓縮感知理論,約束等距特性(restricted isometry property,RIP)是稀疏信號可重構的必要條件,K階約束等距特性定義為,如果存在δK ∈(0,1),使得
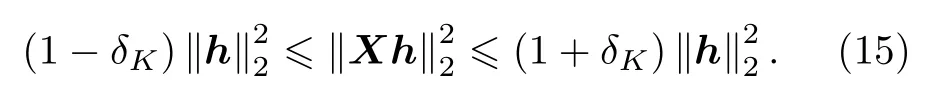
對所有h ∈{h|‖h‖0≤K}都成立,其中如果針對所有K階稀疏矢量h均滿足(15)式的最小常數為δK,則矩陣X滿足K階約束等距特性,δK稱為矩陣X的約束等距常數.
若Δ:RM →RN表示某一種重建算法,則導頻矩陣和重建算法對(X,Δ) 的穩定性[14]定義為:對于任何矢量‖h‖0≤K,e ∈RM,均有
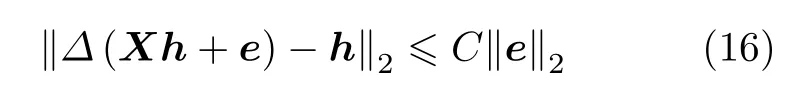
成立,則稱導頻矩陣X和重建算法Δ是C穩定的.如果導頻矩陣和重建算法對 (X,Δ)是C穩定的,則對于所有‖h‖0≤2K,均有
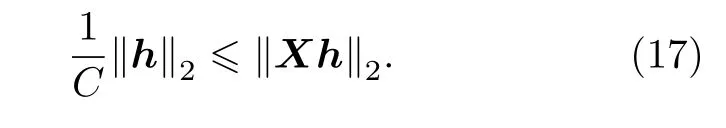
由定義(16)式可以看出,C越小,導頻矩陣和重建算法對(X,Δ) 穩定性越好,重建性能也越好,但是受限于導頻矩陣X的RIP 特性,C不能太小,當C →1時,矩陣必須滿足下限δ2K=1-1/C2→0.因此,如果希望獲得更優的信號重建性能,需要調整矩陣X使它滿足RIP 定義 (15) 式中更大的下界,即更小的δ2K,從而使得C更小.
考慮定義 (15) 式,設矩陣X滿足2K階RIP條件,即?δ2K ∈(0,1),有

對所有的h ∈{h|‖h‖0≤2K}都成立.
利用范數運算與跡運算關系,(18)式可轉化為
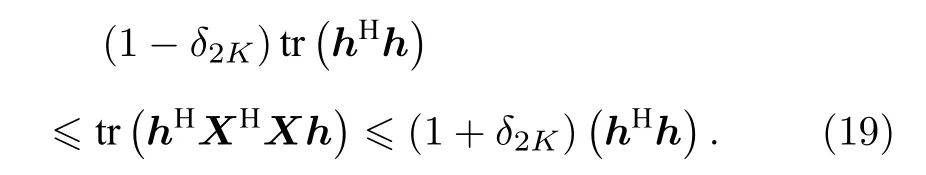
對?‖h‖0=2K,非零分量指標集合Ωi={i(1),i(2),···,i(2K)}.可得:
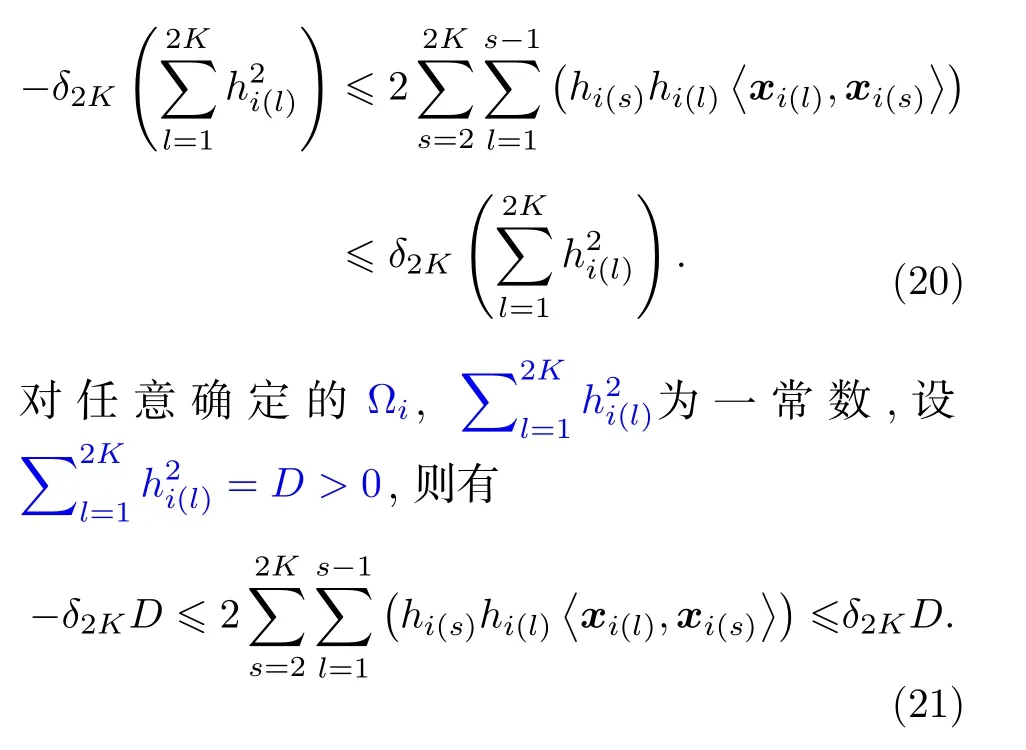
結合定理1,當導頻矩陣X滿足 (14)式,即導頻矩陣列相關性期望的取值越集中且越接近于零時,的取值越有可能在0 附近,此時越有可能滿足更小的δ2K使 (21) 式成立,即使得信號恢復性能越好.
根據以上推理,定理1 可推廣到任意稀疏恢復算法下.
定理2對于任意稀疏信道恢復算法重構錯誤率最小化的導頻矩陣優化準則為
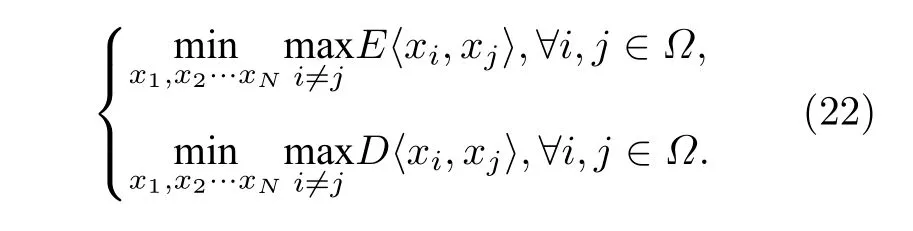
4 導頻優化算法分析與設計
4.1 導頻優化算法分析
設導頻矩陣X ∈RM×N且各列均已歸一化,其自相關矩陣R=XTX,故R為半正定矩陣,可以正交對角化,即:
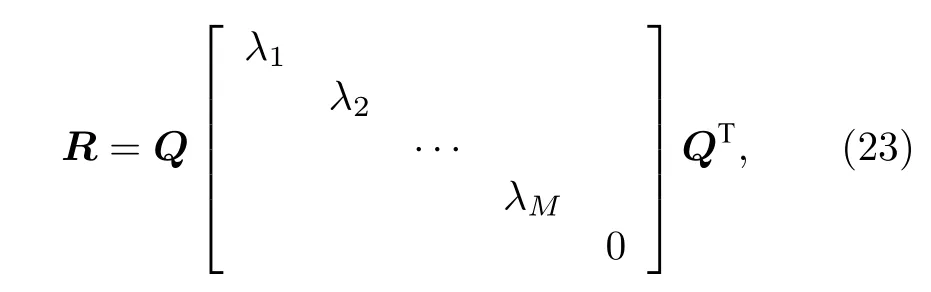
其中,λ1,λ2,···,λM為R的M個大于0 的特征值,Q為N階正交矩陣,由于R的對角線元素均為1,可得
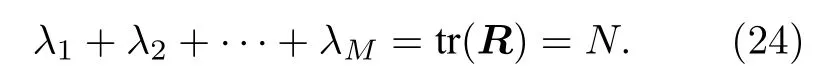
又因為R為實對稱矩陣,有R=RT,則
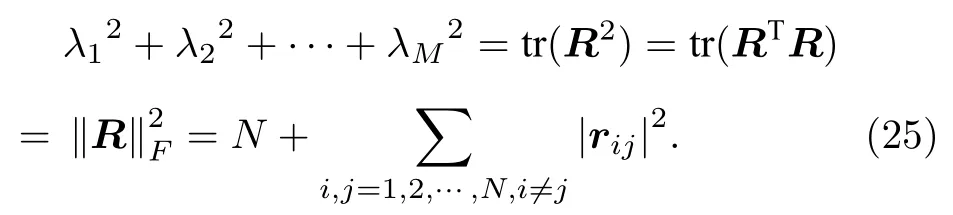
由拉格朗日乘子法,設函數為
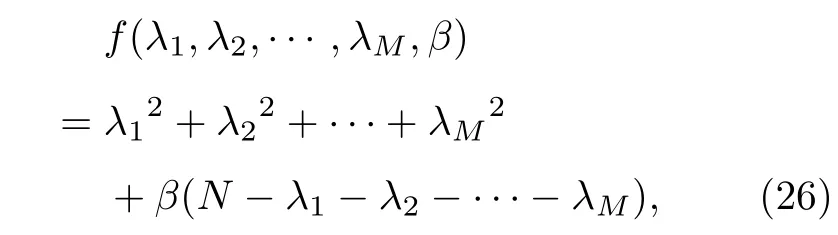
分別對λ1,λ2,···,λM求偏導數,得:
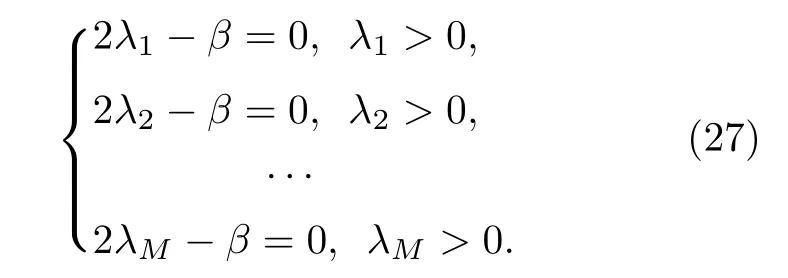
可知極點在λ1=λ2=···=λM處取得,且當λ1=N,λ2=···=λM=0時,
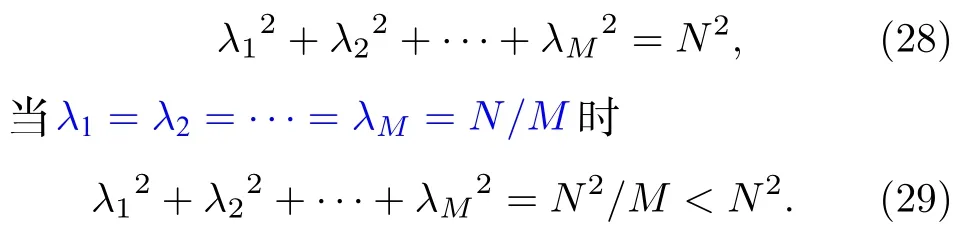
則λ1=λ2=···=λM是唯一極點且不是極大值點,故其為全局最小值點,結合(28)式和(29)式可得
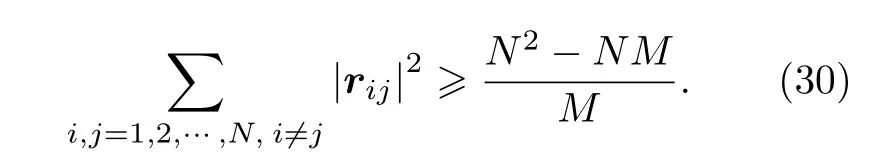
(30)式代表了導頻矩陣各列自相關性之和所能達到的最優下界,令bd=N2-NM/M,同時考慮到矩陣列相關性方差最小化的條件,將自相關性之和的最優下界平均到每一元素作為每一元素的最優下界,記為pd.則
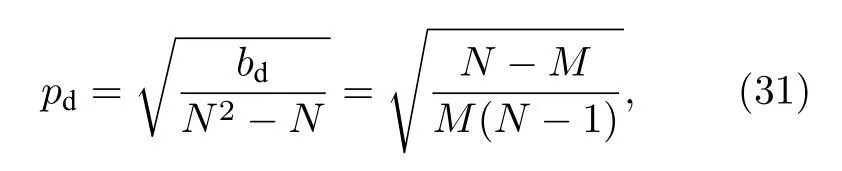
可看出是Welch 界[15].
設參數

(32)式代表了待優化矩陣的平均列相關程度.
通過設定自相關矩陣縮減參數ps使得pd≤ps<pt作為縮減標準對自相關矩陣R中元素進行縮減,即可以達到減小導頻矩陣X列相關性的目的,具體縮減規則設定為
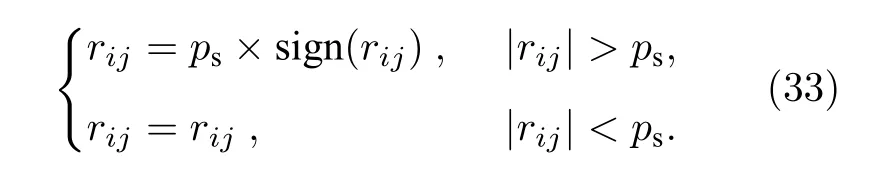
通常經過縮減后的自相關矩陣R會變成滿秩矩陣,但由于R=XTX限定了 rank(R)≤M,故需對縮減后的自相關矩陣做進一步處理,以恢復滿足矩陣秩取值條件的導頻矩陣X.因為矩陣R可以正交分解,所以可以采用裁剪較小特征值的方法來盡可能保留原矩陣中的數值,由R=XTX=,可得
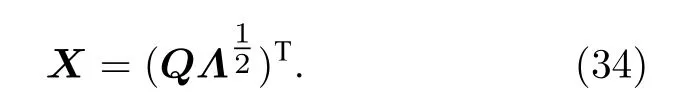
通過保留對角矩陣Λ中最大的M個特征值,根據(34)式即可恢復導頻矩陣X.
4.2 算法設計
根據以上分析,對于任意隨機高斯矩陣,提出自適應自相關矩陣縮減參數導頻優化算法如下.
輸入調整因子α,最優平均相關下界pm
初始化隨機高斯矩陣X ∈RM×N,自相關矩陣R=XTX,待優化矩陣平均列相關程度,縮減參數,縮減自相關矩陣Rs∈RN×N,其中rii=1,rij=ps,i/=j,l=0,m=0,=0.


輸出優化導頻矩陣
5 仿真結果
5.1 信道重構錯誤率
因為實際的信道估計不能達到完全的精確,可認為估計誤差在某一閾值ξ內時估計正確,若經過T次估計,所得估計信道向量集合為12=Υ,定義數列{aT}為
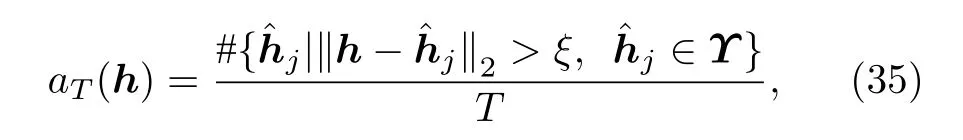
因為0 ≤aT≤1,故其上極限存在,定義信道重構錯誤率為
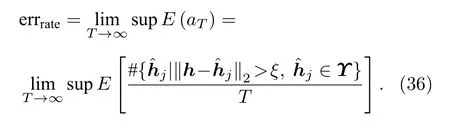
5.2 仿真參數
仿真采用FDD 大規模MIMO 下行鏈路模型,在基站端配置N根天線,每次估計發送M個導頻,信道稀疏度假定為K.各仿真參數說明如表1 所列,特殊參數取值以下特別說明.

表1 仿真參數Table 1.Simulation parameters.
5.3 仿真結果對比分析
圖2 給出了在(7) 式定義下的導頻矩陣相關性隨參數p變化對比情況.從圖2 可以看出,在參數p取值1—20 區間內,各導頻矩陣列相關性均隨著p的增大而增大,其中隨機高斯矩陣增幅最大,為10%—30%,Elad 方法顯著降低了導頻矩陣列相關性,可達到10%—15%,低冪平均列相關方法達到9%—12%,所提方法可以降低到大約9%—10%,已非常接近于理論最優下界8.87%.
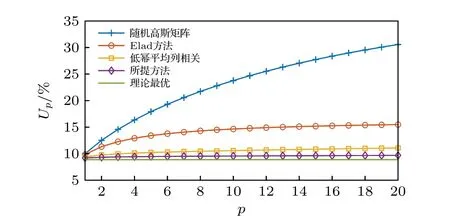
圖2 不同參數 p 定義下的導頻矩陣相關性對比Fig.2.Pilot matrix correlation contrast as defined by different parameters.
圖3 給出了在(6) 式定義下導頻矩陣列相關性隨著發送導頻個數變化的對比圖,可以看出導頻矩陣中列相關性最大的數值.在導頻個數M取值19—57 范圍內,導頻矩陣列相關性均隨著導頻個數的增加而減小.其中隨機高斯矩陣相關性最高,在56%—80%之間.Elad 方法相對隨機高斯矩陣有小幅度降低,在導頻個數小于35 時與后者大體接近,以后隨著導頻個數的增大略微減小,這說明Elad 方法對導頻矩陣最大相關性取值的優化效果不明顯.低冪平均列相關方法隨著導頻個數的增加顯著降低了導頻矩陣列相關性,取值在19%—70%之間,但是在導頻個數較少時還是具有較高相關性.所提方法進一步降低導頻矩陣列相關性至11%—48%,并且在較少導頻個數下便已獲得穩定的效果,隨著導頻個數增加,其相關性取值逐漸趨于最優下界.
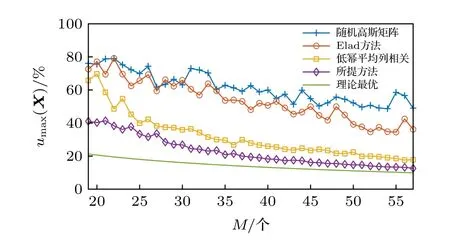
圖3 導頻矩陣相關性隨發送導頻數變化圖Fig.3.Changes of the pilot matrix correlation with the number of transmitted pilots.
圖4 繪制了各導頻矩陣不同列之間相關性取值的分布情況.可以看出,高斯隨機矩陣列相關性分布在0—30%之間較多且分布平均,說明高斯隨機矩陣列相關性方差較大,且存在較多有較大相關性的列,根據第3 節的理論分析,這會對信道恢復的正確率產生不利影響.Elad 方法減小了導頻矩陣列相關性方差,可以看出,當N=128,在N2-N=16256對相關性取值中,大約有2000 對取值集中在16%—17%,其他值則均勻分布在0—16%.低冪平均列相關方法不僅使導頻矩陣列相關性的方差進一步減小,而且相對于Elad 方法得到了更低的期望值,可以看到,大約有7000 對相關性取值分布在9%—13%之間.所提方法在9%—11%區間內聚集了大約8000 對相關性取值,其導頻矩陣列相關性期望和方差均小于上述方法.
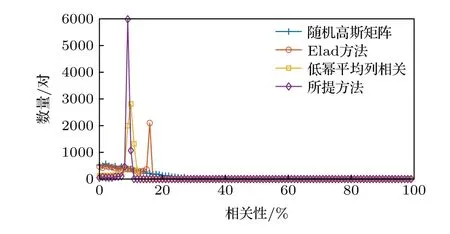
圖4 導頻矩陣列相關性取值分布圖Fig.4.Column correlation value distribution of pilot matrix.
圖5 給出了OMP 算法信道估計下重建錯誤率隨稀疏度變化情況,可以看出,在信道稀疏度K取16—32 范圍內,各導頻矩陣下的信道估計錯誤率均不斷上升,在稀疏度K=16 時,高斯隨機矩陣重構錯誤率最高為7.6%,Elad 方法和低冪平均列相關方法均有效降低了信道估計的錯誤率,達到2.00%和0.45%,所提方法達到了四者中最低的信道重構錯誤率0.3%.分別比前三種方法降低了96%,85%和50%.說明所提方法對進一步提高信道估計的可靠性有真實效果.
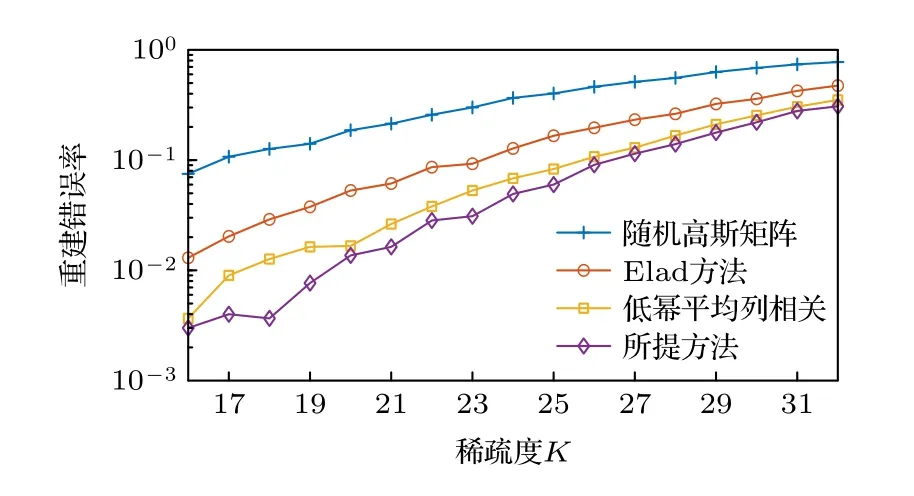
圖5 信道重構錯誤率隨稀疏度變化圖Fig.5.Channel reconstruction error rate change with sparsity.
圖6、圖7 分別給出了稀疏度K=8 和K=16時,OMP 信道估計下重購錯誤率隨導頻個數的變化情況.從圖6 可以看出,在K=8 時,各方法的信道重構錯誤率隨著導頻個數的增多而不斷減小.其中隨機高斯矩陣最高,在導頻個數范圍為21—32時,低冪平均列相關方法重構錯誤率略高于Elad方法,之后則大體重合.所提方法在相同稀疏度下的重構錯誤率與以上兩種方法相比,大約降低了5%,說明了所提方法在低稀疏度且發送較少導頻時具有更好的表現,這對于考慮到節省導頻開銷的實際場景是有意義的.
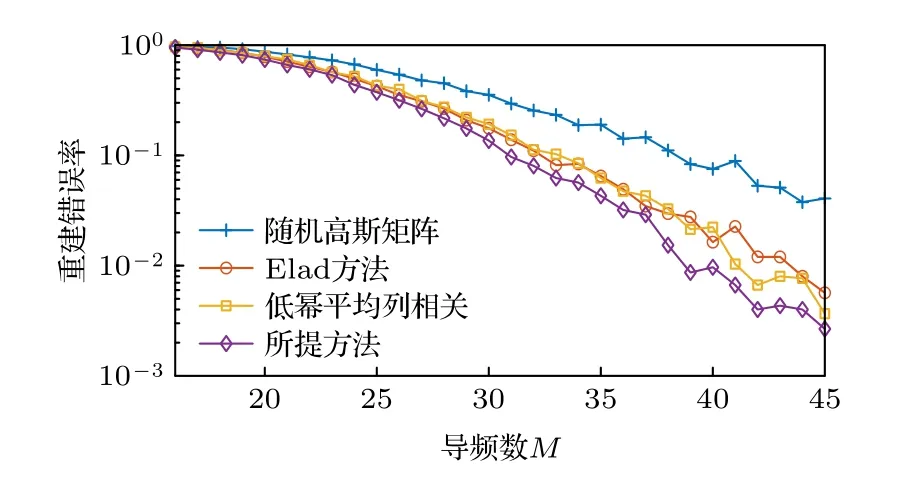
圖6 信道重構錯誤率隨導頻個數變化圖(K=8)Fig.6.Channel reconstruction error rate with number of pilots (K=8).
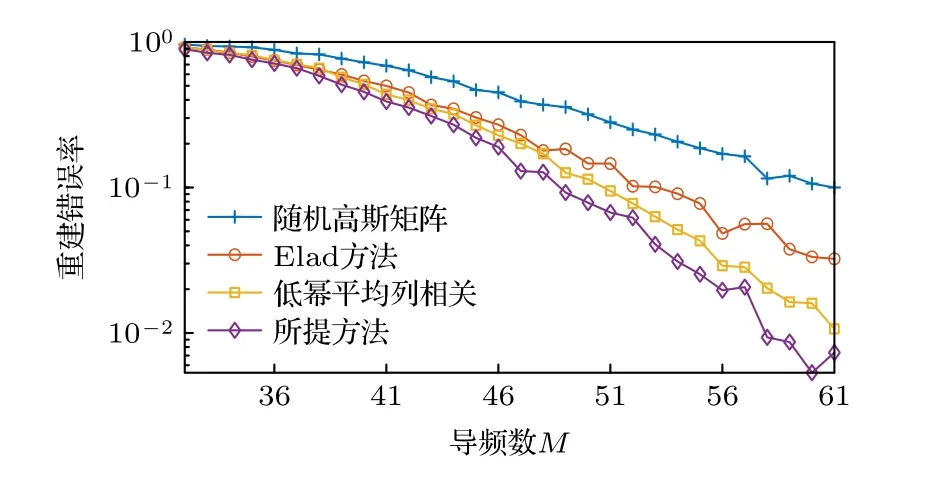
圖7 信道重構錯誤率隨導頻個數變化圖(K=16)Fig.7.Channel reconstruction error rate with number of pilots (K=16).
從圖7 可以看出,在信道稀疏度K=16 時,重構錯誤率明顯增大.低冪平均列相關方法與Elad方法在M取值范圍30—42 時大體重合,所提方法則比以上兩種方法降低5% 左右,在M取值范圍43—60 時,低冪平均列相關方法比Elad 方法有所降低,所提方法則具有四者中最低的信道重構錯誤率.說明所提方法在較為復雜的信道環境中,在保證一定的發送導頻數量的前提下,依舊具有良好的信道重構性能.
6 總結
本文首先理論分析了OMP 算法下信道重構錯誤率與導頻矩陣之間的關系,得出了優化導頻矩陣的兩條準則:導頻矩陣列相關性期望和方差最小化.然后依據優化準則分析了優化導頻矩陣的方法,并設計出相應的自適應自相關矩陣縮減參數導頻矩陣優化算法.仿真結果表明,該方法有效降低了導頻矩陣列相關性期望和方差.在采用OMP 算法進行信道估計時,所設計出的導頻矩陣降低了信道重構錯誤率,提高了信道估計的可靠性.
附錄A 定理1 證明
A1 OMP 算法相關性計算
由OMP 算法中殘差和已選取列空間的正交性可知,當j ∈Ω(m)時,(10)式中的取索引值(m),可計算出第m+1 次迭代的相關性數值:
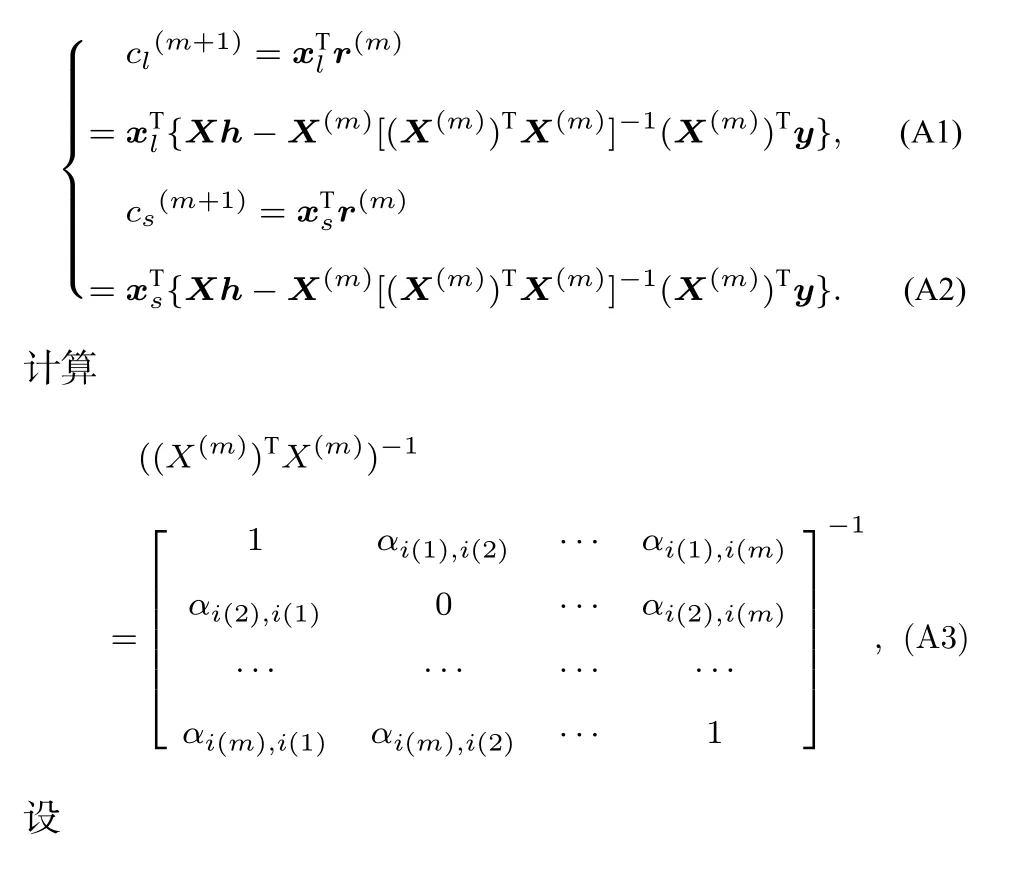

根據矩陣求逆引理[16],
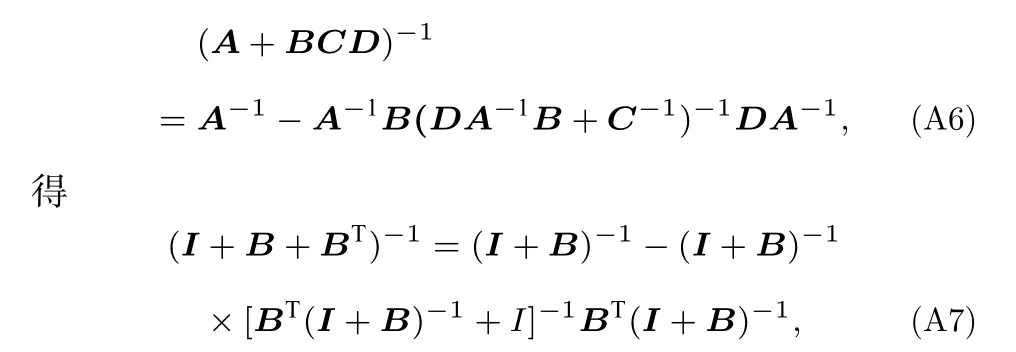
因為B為冪零矩陣,(I+B)-1可級數展開為
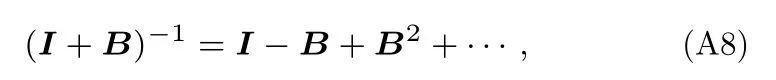
忽略2 次及以上的高次冪,取
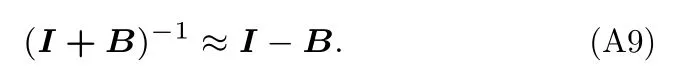
(34)式可化簡為
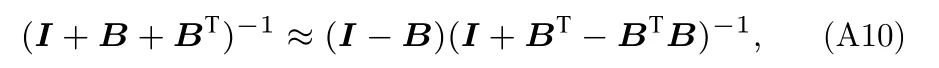
其中,BTB非常接近于零矩陣,取BTB ≈0,同樣(I+BT)-1可級數展開為
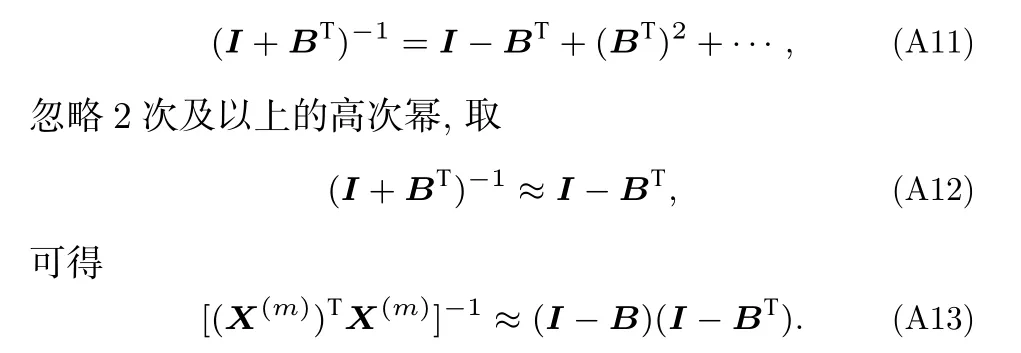
結合(A13)式,通過計算,(37)式可進一步展開為
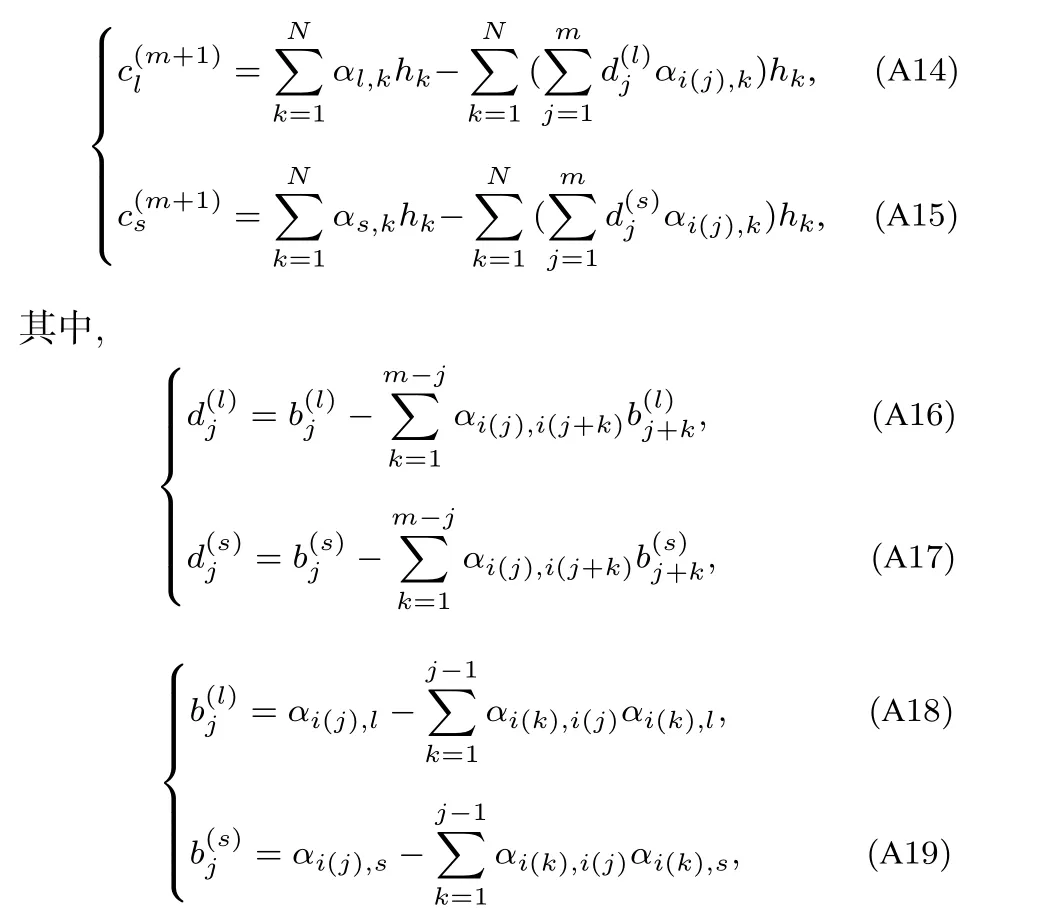
(A14)式和(A15)式是OMP 算法在第m+1 次迭代時,在索引l和s處的相關性數值表達式.
A2 OMP 算法重構錯誤率與導頻矩陣的關系分析
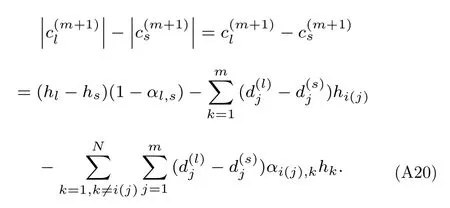
假設導頻矩陣X各元素為服從獨立同分布的隨機變量,則各列相關性〈xi,xj〉,i,j ∈Ω,i/=j的期望和方差可分別計算為
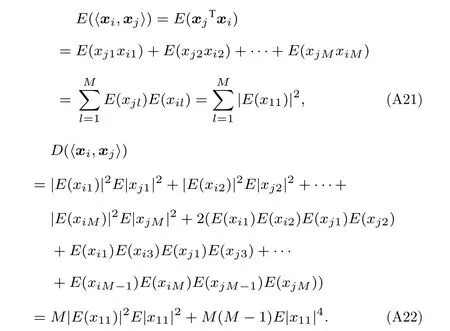
可看出E(〈xi,xj〉)和D(〈xi,xj〉) 均為常數,設:
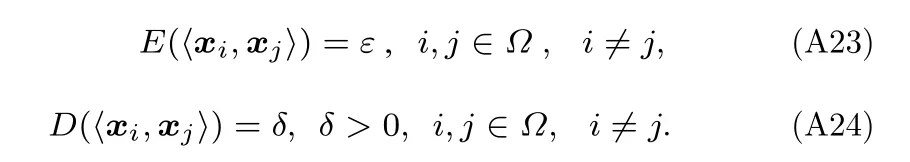
根據(A23)和(A24)式,對(A20)式左右兩端取期望值,其右端可做以下處理:
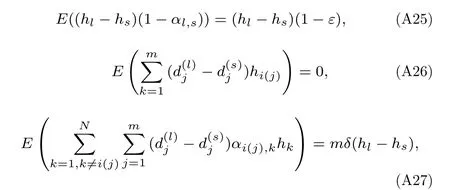
將(A25),(A26)和(A27)式代入(A20)式,可得:
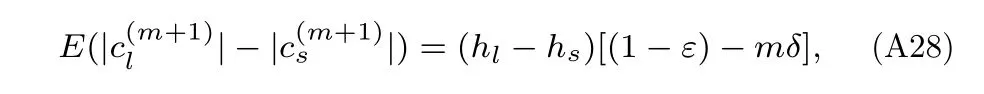
(A28)式表示對指標l,s代表的位置進行相關性判決后的期望值,因為l ∈Ωi為信道非零分量位置指標,s∈/Ωi為信道零分量位置指標,根據(12)式,當
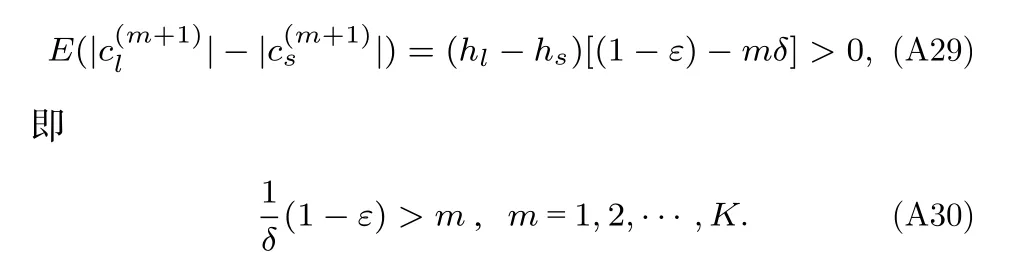
相關性判決的期望選擇了信道非零分量指標l,判決正確,令,為了盡可能減小判決出現錯誤的可能性,應使
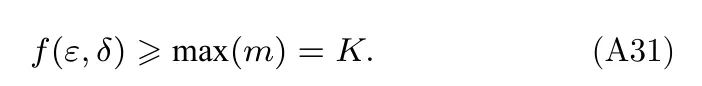
可見f(ε,δ)取值越大,則信道重構錯誤率越小,因為f(ε,δ)是關于自變量ε和δ的減函數,所以應取盡可能小的ε和δ使f(ε,δ)增大,故對于導頻矩陣X,使OMP 算法重構錯誤率最小化的條件為