基于AHP和DEA模型的高等教育測評系統

周子恒 葉思遠 黃運煒

摘要：為有效應對新型冠狀病毒肺炎疫情帶來的教育領域相關威脅，文章建立了基于AHP和DEA模型的高等教育測評系統。依托一系列指標并利用層次分析模型獲得各指標權重，評判高等教育水平的健康狀況。該文選取了幾個不同發展水平的國家進行實驗分析，并對得分最低的國家進行了問題探討，根據可持續模型為其設計發展藍圖。利用上述建立的兩個模型對藍圖進行衡量，發現該國在實行有關政策后，在較長階段內高等教育得到穩步提升，證明了整個測評系統的有效性。

關鍵詞：AHP模型;DEA模型;高等教育模型;投入產出

中圖分類號：TP3 ? ? ? ?文獻標識碼：A

文章編號：1009-3044（2022）02-0069-03

高等教育作為一個產業本身，應該考慮如何大力發展和可持續發展。作為國家重點人才培養的源頭，也要考慮其系統的整體性和健康性[1]。特別是在充滿變化和挑戰的21世紀，各國都應該對高等教育體制進行創新和改革，以適應時代的發展。世界各國的高等教育體系都有不同的教育形式，也有權威機構對所有國家的高等教育系統進行排名[2-3]。各種不同的評價標準往往帶來了高等教育評定的差異。因此，建立一個更加健康、可持續的高等教育體系顯得尤為重要。然而，改變往往是困難的。這一制度建立后，必須突破思維固有的局限，勇于創新，勇于改革，才能真正實現高等教育的進步與發展。

1 模型介紹

1.1 本文所使用到的符號

表1列出了本文中使用的符號和含義。

1.2 HES健康評價模型

1.2.1 模型描述

層次分析法（AHP）通過分析影響決策的各種因素，促進整體決策的制定。由于層次分析法易于理解和使用，可以使模糊的問題清晰，定性的問題定量[4]。它在現實生活領域中得到了廣泛的應用，教育系統的評價也不例外。層次分析法的基本步驟分別是構建層次結構模型、構造比較判斷矩陣、計算特征向量和進行一致性檢驗，具體流程如圖1所示。

1.2.2 HES健康評價模型的度量

通過對不同國家高等教育體系排名結果進行對比，確定健康標準指標。本文從目前公認的四大權威排名確定健康標準的一級指標及二級索引[5]。該指標從機會成本、公平資助等方面評價教育體系的健康程度，如表2所示將衛生標準定義為H，將4個一級指標變量分別命名為IR、IO、IC、ISE，分別代表資源、產出、合作和社會環境。然后列出H與指標變量的關系：[H=ω1IR+ω2IO+ω3IC+ω4ISE]。同樣，可以得到第一級指標和第二級指標的關系：

[MR=ω11IR1+ω12IR2]

[MO=ω21IO1+ω22IO2+ω23IO3]

[MC=ω31IC1+ω32IC2]

[MSE=ω41ISE1+ω42ISE2+ω43ISE3]

其中ω_i為一級指標權重，ω_ij為二級指標權重。指標權重結果將在下一節通過層次分析法說明。

1.2.3 判斷矩陣及指標權值確定

規則層Bi權重向量B=（B1， B2， B3， B4），[inBi=1]，指標層C=（C1， C2，…，Cn），滿足[inCi=1].。根據模型和相應的指標體系，Ai和Bi由計算所得來表示。

[A=aij]，[ aij>0， aij=1aji， aii=1]

根據矩陣A的元素判斷每一行乘積[Mi=j=1naij]，類型n為矩陣階數;計算所有M_i的幾何平均值，M?_i表示[Mi=Min];一級指標Ai的權重重用ω_i，二級指標Bi的權重重用ω_ij。將權重值歸一化，計算如下：[ωi=Mii=1nMi]

計算一致性指標：[CII]=[λmax-nn-1]，參照表3中同階矩陣的平均一致性指標RI，然后計算一致性比CR=CI/RI，得到結果CR<0.1即A具有完全一致性。

一級指標的最終權重見表4。

1.3 HES可持續評價模型

1.3.1 模型簡介

在一個穩定的環境中，系統的效益大于成本，就可以認為這個系統可持續，為了說明可持續這個結果，通過DEA模型來定義這個投入產出的效率比，表5為該模型的指標[6]。

對于一個國家而言，每年為一個DMU（決策單元），每個DMU有2種投入和3種產出，設[xij ]是第j個DMU的第i種投入量，[yrj ]是第j個DMU的第r種產出量，[vi ]表示第i種投入的權值，[ur]是第r種產出的權值，向量[xj]，[yj]是決策單元j的輸入和輸出向量，v和u分別是輸入和輸出權值向量。則有：[xj]=（[x1j，x2j]）T，[yj]=（[y1j，y3j，y3j]）T，u=（[u1，u2]）T， v=（[v1，v2，v3]）T

定義決策單元j的效率評價指數為[hj]：

[hj=uTyjvTxj， （j=1，2，3）]

根據層次分析模型順利求出輸入輸出權重，分別為資源20%、社會環境20%、合作20%、產出40%。

2 實驗進行及結果

通過分別統計美國、日本和馬來西亞的數據[7]，然后將這三個國家的指標數據帶入模型得到結果，如圖3所示。

從圖3可以看出，三個國家中，美國得分最高，日本得分緊隨其后，而馬來西亞得分最低。同時在實驗模擬過程中發現，美國在測評的各個板塊中都取得了極高的分數。而日本在資源及社會環境方面具有一定的優勢，但投入產出較低。而馬來西亞在國際合作領域具有一定的優勢，但是產出方面劣勢。以上結果導致了三國得分不同。

3 預期藍圖及設想

3.1 藍圖介紹

根據層次分析法，主要因素對高等教育系統的健康狀況影響的先后次序為：科研產出25%、教學投入、科研投入、雇主評價、校企合作、國際合作均為10%、師生比8%、人均所受高教率7%、大學總數量7%、人均GDP5%。可見，科研產出、教學科研投入等占比很大。

鑒于以上標準，可以認為從以下幾點為此類高等教育急需改善的國家設計發展藍圖。首先，加大高等院校的資金投入，增大教師收入，提高教師滿意度。其次，加大對教師、學生在論文發表、國際競賽等領域的宣傳和獎勵，調動積極性。同時，重視國內經濟發展，增大國內就業機會和薪資待遇。當然加大本國教師數量勢必降低國際教師人數，但可以增加國際交流和學術合作以減輕這一影響帶來的劣勢[8]。

3.2 測評模型

根據以上藍圖，該國政府積極采取相關政策，一年后各板塊得分發生了一些變化，如圖4所示。

指標的變化導致投入產出效率的變化。使用上述模型：

[hj=uTyjvTxj， （j=1，2，3）]

計算結果為：1.14>1，即產出大于投入，系統在下一年度能夠持續實施該政策。

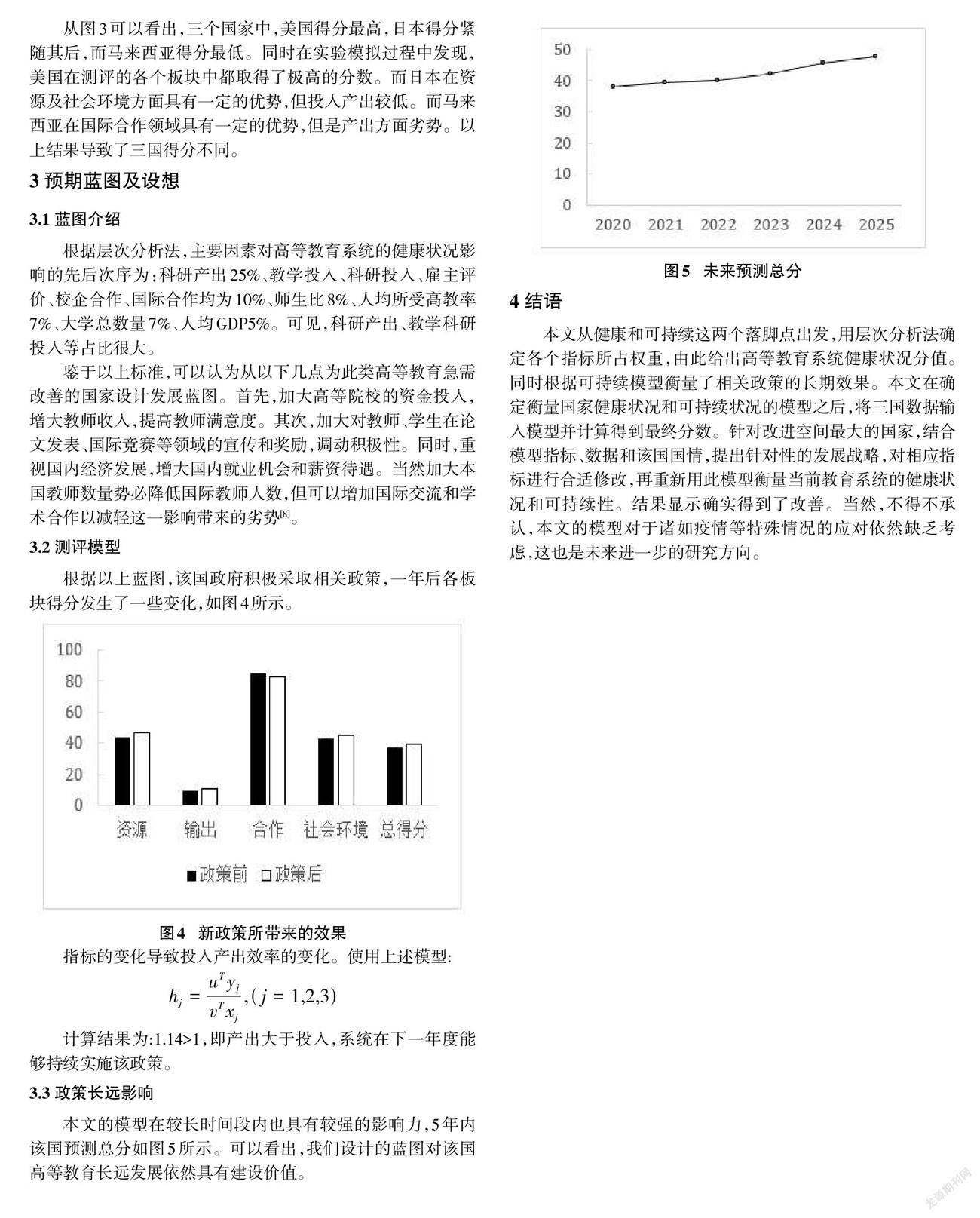
3.3 政策長遠影響

本文的模型在較長時間段內也具有較強的影響力，5年內該國預測總分如圖5所示。可以看出，我們設計的藍圖對該國高等教育長遠發展依然具有建設價值。

4 結語

本文從健康和可持續這兩個落腳點出發，用層次分析法確定各個指標所占權重，由此給出高等教育系統健康狀況分值。同時根據可持續模型衡量了相關政策的長期效果。本文在確定衡量國家健康狀況和可持續狀況的模型之后，將三國數據輸入模型并計算得到最終分數。針對改進空間最大的國家，結合模型指標、數據和該國國情，提出針對性的發展戰略，對相應指標進行合適修改，再重新用此模型衡量當前教育系統的健康狀況和可持續性。結果顯示確實得到了改善。當然，不得不承認，本文的模型對于諸如疫情等特殊情況的應對依然缺乏考慮，這也是未來進一步的研究方向。

參考文獻：

[1] Zhang Yong-min， Zhao Shi-dong，erburg P H. ClUE -S model and its application to land use spatial and temporal change simulation of Naiman gas[J].Journal of Natural Resources，2003（3）：3.

[2] Yang Yuan-yuan，Dai Er-fu，Fu Hua.Research on the value of ecosystem services based on InVEST model[J].Journal of Capital Normal University （Natural Science Edition），2012，33（3）：41-47.

[3] Lei J C，Liu J X，Yong F，et al.Multi-scenario ecosystem service assessment of Wuma river valley based on Clue-S and InVEST models[J].Journal of Ecology and Rural Environment，2017，33（12）：1084-1093.

[4] WANG Y L，MA K，JIANG W B.Preliminary report on salt tolerance test of five fruit trees[J].China Fruits，1990（3）：8-12.

[5] Mi Yin-fa，Ma Feng-wang，Ma Xiao-wei. Effects of rhizosphere hypoxia on growth and endogenous hormones of kiwifruit seedlings with different resistance[J]. Acta Horticulturae Sinica， 2009 ， 36（2）：163-170.

[6] WANG C X，CHENG B S，LI Y Z，et al. Screening of salt-tolerant variants in Chinese kiwifruit [J].Journal of Nuclear Agriculture，1990，4（4）：206-212.

[7] ZHOU L M，WANG F，WANG J.Directional screening of salt-tolerant mutants in kiwifruit by EMS mutagenesis[J].Acta Agriculturae Boreali-occidentalis Sinica， 2009，18（5）：330-335，340.

[8] WEI Y，RUAN Z，LAND CHANGE SCENARIO simulation of Liuzhou City in 2025 based on CLUE-S model[J].Journal of Anhui Agricultural Sciences， 202，48（1）：76-79.

【通聯編輯：代影】

1795500511222