低雷諾數下串列布置雙圓柱渦激振動特性研究1)

涂佳黃 黃林茜 何永康 呂海宇 梁經群

(湘潭大學土木工程與力學學院，湖南湘潭 411105)

引言

渦激振動現象廣泛存在于實際工程中,如海洋立管[1]、橋梁拉索[2]、高層建筑[3]等.彈性支撐結構體置于一定速度的流場中,會在其兩側產生交替脫落的旋渦,并誘發結構表面產生流體脈動力,引起結構振動.當彈性支撐結構的振動頻率與渦脫落頻率基本重合時,引發共振,從而對結構造成不可逆的破壞[4].因此,對于渦激振動問題一直是研究的熱點之一,并取得了一系列成果[5-8].

在實際工程中,結構往往以結構群的形式出現,因此對圓柱群渦激振動問題進行研究具有重要意義.影響渦激振動的主要參數包括雷諾數[9]、剪切率[10]、質量比[11]、間距比[12]、頻率比[13]等.近些年來學者們關于各個參數對圓柱渦激振動的影響開展了大量的研究.Papaioannou 等[14]對不同間距比工況下串列雙圓柱與單圓柱工況渦激振動問題進行了研究,當間距比較小時,上游圓柱所對應的鎖定區間較單圓柱工況明顯擴大,但當間距比超過臨界間距比時,上游圓柱基本不受下游圓柱影響,其振幅與單圓柱工況相似.Mittal 和Kumar[15]對Re=100 工況下,串列和錯列布置雙圓柱體流致振動進行了數值模擬,當圓柱排布方式從串列布置轉變為并列布置時,雙圓柱結構運動軌跡將從“8”字形轉變為“橢圓”形.及春寧等[16]對Re=100 條件下,串列雙圓柱在不同情況下的流致振動進行了數值模擬研究,發現無論上游圓柱固定或者振動,下游圓柱的振幅會強于上游圓柱.Qin 等[17]對串列布置雙圓柱體進行了實驗研究,在不同的頻率比工況下分別發現了鎖定、渦激發以及馳振等不同的振動機制.陳文曲等[18]運用分塊耦合法對下游圓柱渦致振動的升阻力特性進行了模擬研究,發現結構表面升力的變化和渦脫落模態以及初始渦脫落時刻之間的內在聯系.鄒琳等[19]運用動網格技術對Re=100 條件下串列雙圓柱渦激振動響應進行數值模擬研究,發現在不同間距比工況下,下游圓柱升阻力系數在折減速度Ur=7.2 附近會出現“跳躍現象”,并出現阻力峰值.陳威霖等[20]對小間距比下串列雙圓柱尾流耦合機制進行了模擬研究,發現由于串列雙圓柱之間平衡位置差的調和當間距比L/D=1.1 時,在較廣的折減速度區間內圓柱會發生大振幅運動.段松長等[21]研究了錯列角度對雙圓柱渦激振動的影響,當折減速度較小時,柱體升阻力系數隨錯列角度的增大而增大,當錯列角度固定時,折減速度的改變對升力影響較大而對阻力影響較小.Ryan 等[22]對層流范圍內臨界質量比進行了探究,當Re=40～ 95 范圍內存在臨界質量比,且其值隨著雷諾數的增大而減小.Chen 等[23]對間距比L/D=1.2～ 5.0 范圍內串列三圓柱進行數值模擬研究,并分析了平衡位置偏移、低頻振動以及漩渦脫落與圓柱之間的時機3 個關鍵因素對馳振現象的影響.

綜上所述,目前研究者們對于影響多圓柱渦激振動參數的探討大多集中在取兩到3 個變量,且多集中在對雷諾數、間距比、剪切率等關鍵參數影響的研究,而對不同頻率比的影響研究較少.然而,在實際工程中,結構會受到多種環境參數變量的影響.因此,本文基于四步半隱式特征線分裂算子有限元方法對層流條件下串列雙圓柱雙自由度渦激振動問題進行了模擬研究,主要分析了頻率比(r=1.0,1.5,2.0),間距比(L/D=2.5,3.5,5.5),剪切率(k=0.0,0.05,0.1)以及折減速度(Ur=3～ 20) 4 個關鍵參數對結構動力響應、尾渦特性、頻譜特性、相位特征與能量傳遞方面的影響,并揭示其內在機理,為實際工程應用提供參考依據.

1 流固耦合數值方法

1.1 流體控制方程

基于任意-拉格朗日歐拉方法下不可壓縮黏性流體N-S 方程的無量綱形式表達如下[24]

式中,xi與xj分別為i,j方向空間坐標;ui與p為流體速度與壓力;cj=uj-wj,其中wj為網格移動速度,cj為流體相對于wj的對流速度;t為時間;雷諾數Re=UcD/ν,其中D與Uc分別為特征長度尺寸與中心來流速度,ν為流體動力黏性系數.

1.2 固體控制方程

彈性支撐圓柱結構運動體系可假設為質量-阻尼-彈簧系統,雙自由度運動結構的控制方程無量綱形式如下

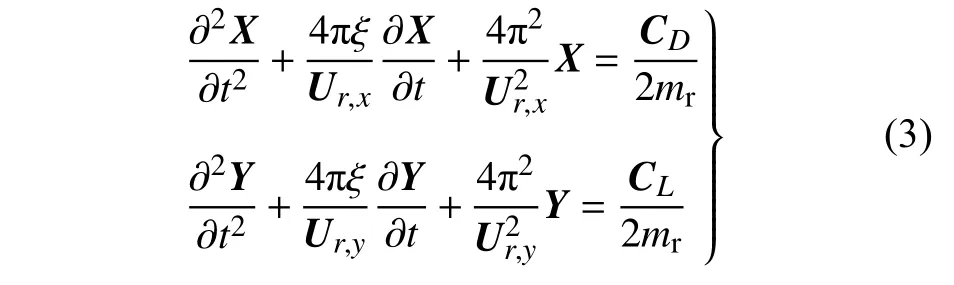
式中,X與Y分別為結構順流向和橫流向無量綱位移;ξ為結構阻尼系數,為了得到最大結構位移響應,取ξ=0;Ur,x=Uc/(fn,xD)和Ur,y=Uc/(fn, yD)分別為x方向(順流向)與y方向(橫流向)折減速度,其中fn,x和fn,y分別為彈性支撐圓柱體結構的順流向和橫流向自然頻率;分別為阻力系數和升力系數;mr=m/(ρD2)為結構折合質量,其中m為單位長度結構質量,ρ為流體密度.本文采用Newmark-β時間積分法求解結構動力方程.

1.3 網格更新

為了避免網格失效,本文對Laplace 方程的邊值問題方法進行了改進,采用改進的Laplace 方程對網格坐標進行更新[25]

式中,Si為網格節點i方向位移;Гm和Гf分別為網格動邊界和固定邊界;gi是運動邊界上的節點位移;τ是網格形變控制參數,表達式如下

式中,Δe為計算網格單元的面積(或體積);Δmin和Δmax分別為網格單元中最小與最大的面積(或體積).本文采用Galerkin 有限元方法求解該Laplace 方程的邊值問題.

1.4 計算流程

本文采用分區迭代方法求解鈍體結構渦激振動問題,該算法的計算流程如下:

(1) 求解流體控制方程:運用基于四步半隱式CBS 穩定化有限元方法求解流體控制方程式(1)和(2),獲得t(n +1)時刻流場速度與壓力,從而得到流體作用于結構上的流體力.

(2)求解固體控制方程:將流體力施加到結構,以Newmark-β時間積分方法求解結構運動控制方程式(3),得到t(n +1)時刻結構的動力響應.

(3) 網格更新:采用Galerkin 有限元方法求解Laplace 方程式(4),獲得網格節點位移及網格速度,并更新網格坐標.

(4)返回第一步開始計算t(n +2)時刻,并循環至系統達到穩定為止.

本文的數值方法已運用于渦激振動相關問題求解過程中,并能得到較好的數值結果[26-28],驗證其正確性與可靠性.

2 問題描述

2.1 計算模型

基于上述方法本文對串列雙圓柱流致振動問題進行了數值模擬研究,其計算模型如圖1 所示,兩圓柱在橫流向與順流向均可自由振動,選取雷諾數Re=100,其他參數選取為:間距比L/D=2.5,3.5,5.5;剪切率k=0.0,0.05,0.1;固有頻率比r=fn,x/fn,y=1.0,1.5,2.0;折減速度Ur=Ur,x=3～ 20;質量比mr=7.85.計算域尺寸為[-30D,60D] × [-10D,10D],上游圓柱(upstream cylinder,UC)的圓心位置為(0,0),下游圓柱(downstream cylinder,DC)的圓心位置為(L/D,0).本文計算域堵塞率B=5%,邊界條件設置如下:模型入口設定為速度入口ux=Uc+ky(Uc=1.0),uy=0;模型出口設定為壓力出口p=0;上下邊界均為自由滑移邊界?ux/?y=0,uy=0;結構表面為無滑移壁面u x=uy=0.對于彈性支撐圓柱體結構,為了獲得較大的結構動力響應,故不考慮阻尼影響,將其簡化成質量-彈簧系統模型,其量綱歸一化時間步長設為Δt=0.002.

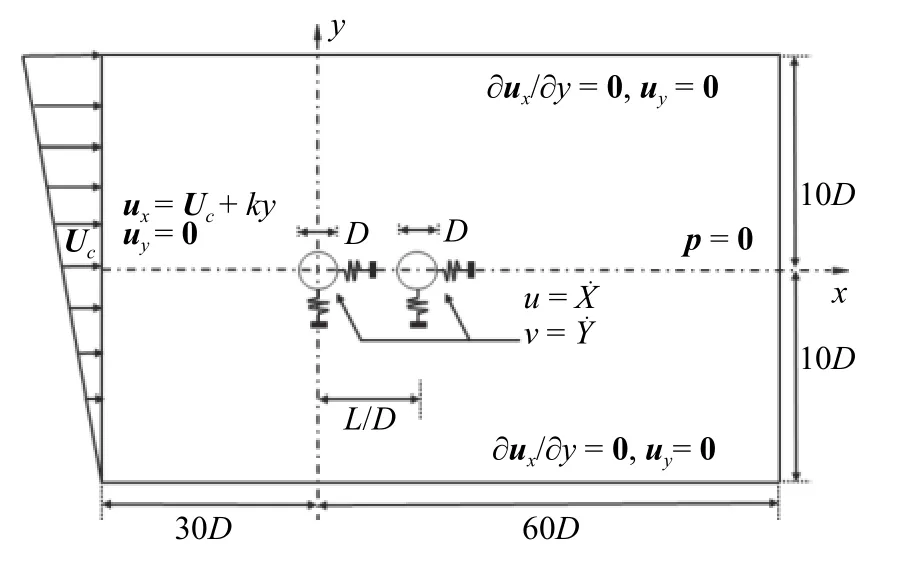
圖1 計算模型與邊界條件Fig.1 The computational model and boundary conditions

2.2 網格劃分

本文流場計算域采用非結構化三角形網格劃分法,為了更準確的刻畫出圓柱尾渦的形成與發展,故對圓柱附近及尾流區域進行網格加密處理.由表1 可知,與密網格GIII 相比,網格GI 的Xmax/D與Ymax/D的計算結果最大變化率分別為6.25%和4.96%;網格GII 的最大變化率分別下降為0.33%和0.06%.由于網格GII 已滿足數值模擬結果網格收斂性要求和計算精度要求,且若采用密網格GIII,雖能獲得更高的計算精度,但計算耗時會大幅度增加,效率降低.綜上所述,本文所有算例采用的網格密度和分布情況與GII 類似.

表1 網格獨立性驗證:串列布置雙圓柱流致振動計算結果(L/D=2.5,r=1.0,k=0.0, Ur=6.0)Table 1 Grid independence test:the results for the two tandem circular cylinders at L/D=2.5,r=1.0,k=0.0, Ur=6.0

3 計算結果與分析

3.1 振幅特性

本文對不同剪切率,固有頻率比,間距比以及折減速度工況下串列布置雙圓柱雙自由度流致振動振幅變化情況進行了分析.由圖2 可知,圓柱橫流向振幅要遠大于其順流向振幅,且UC 的共振區間明顯要寬于DC 的共振區間.整體上看,頻率比較小工況(r=1.0 與r=1.5)對UC 振幅值變化影響較小,其幅值隨折減速度的變化較為接近,但當r增大到2.0 時,UC 在兩個自由度方向的振幅明顯增大.一方面,當頻率比較大時,x,y方向的結構剛度不同,使其容易受到流體脈動力的影響,進而導致脈動力引發的振動越大.另一方面,可能由于此時圓柱流向振動和橫向振動同時達到共振有關,雙頻共振的出現使得頻率比為2.0 時,圓柱振幅明顯增大.特別的是,UC 在兩個自由度方向達到最大振幅值的折減速度不同,而DC 基本同步.另外,由于來流以及間隙流的干擾,使得UC 與DC 兩者“鎖定區間”的折減速度范圍存在差值,UC 較DC 更早進入共振狀態,同時也會更早退出.

圖2 不同頻率比與剪切率工況下,串列雙圓柱雙自由度最大振幅隨折減速度的變化(L/D=2.5)Fig.2 The variation of the maximum vibrating amplitude of tandem double cylinders with reduced velocity under different frequency ratios and shear rates in two degrees of freedom (L/D=2.5)

圖2 不同頻率比與剪切率工況下,串列雙圓柱雙自由度最大振幅隨折減速度的變化(L/D=2.5) (續)Fig.2 The variation of the maximum vibrating amplitude of tandem double cylinders with reduced velocity under different frequency ratios and shear rates in two degrees of freedom (L/D=2.5) (continued)

3.1.1L/D=2.5

當折減速度(Ur=3～ 4) 較小時,兩圓柱在x,y方向僅微弱振動,振幅接近于零.當Ur=5 時,振幅開始“啟動”,UC 在橫流向的振幅值迅速增大,逐漸進入鎖定狀態.然而,順流方向僅在r=2.0 工況下圓柱體結構會發生明顯的振幅,在其它頻率比(r=1.0,1.5)工況下,UC 基本不振動,如圖2 所示.由圖3 可知,r=1.0 與r=1.5 工況所受到的流場時均壓力基本相同,UC 迎流面受到來流的沖擊作用受到正壓,其尾部由于渦流的脫落產生吸力受到負壓作用.當r=2.0 時,UC 受到的正壓面積更廣,與此同時DC 的前駐點附近開始出現正壓,兩圓柱尾部負壓面積均增大,這可能是該工況比其它兩個工況振幅更大的原因,如圖3(c)所示.隨Ur進一步的增大,圓柱開始進入“鎖定區間”(Ur=5～ 10),在此區間內圓柱的振動頻率與渦脫落頻率無限接近,從而誘發共振現象.由圖2 觀察到兩圓柱在橫流向的振幅值迅速增大,并在不同的折減速度處取得極值.另外,UC 在不同自由度方向上被“完全鎖定”的折減速度不同,其橫流向振幅最大值在Ur=7 處取得,其值為0.82(k=0.05,r=2.0).然而,在Ur=5 時順流向振幅達到最大值,其值為0.19(k=0.0,r=2.0).對于下游圓柱則沒有出現錯位現象,DC 在兩個自由度方向上被“完全鎖定”的折減速度相同,其橫流向上最大振幅值達到了1.36(k=0.0,r=2.0)是UC 的1.7 倍,順流向上最大振幅值為0.24(k=0.0,r=2.0)是UC 的1.3 倍.當Ur≥9 時,UC 退出鎖定區間,在兩個流向上的振幅均趨于穩定,橫流向最大振幅值維持在0.2 附近,而順流向最大振幅值已趨于零.然而,DC 橫流向的振幅在Ur=9 時,還維持著較大的振幅值1.0.隨著Ur的繼續增大DC 在x方向的振幅值為0,在y方向的振幅由1.0 遞減到0.2 左右,當Ur≥16 時,UC 與DC 在兩個流向的振幅值均趨于0,兩圓柱體結構不再發生振動.

圖3 k=0.0 與Ur=7 時,不同頻率比下流場無量綱時均壓力圖Fig.3 Dimensionless time-averaged pressure diagram of flow field at different frequency ratios at k=0.0 and Ur=7

3.1.2L/D=3.5

當間距比增大到3.5 時,UC 與DC 在兩個自由度上最大振幅值變化規律與L/D=2.5 工況大致相同,UC 在Ur=6 處Ymax/D值最大,其最大值為0.79(k=0.05,r=2.0),而DC 在Ur=8 處Ymax/D值最大,其最大值為1.33(k=0.1,r=2.0),如圖4 所示.其中,UC 的振幅變化趨勢較為規律,而DC 較為特殊.特殊在于:均勻來流工況下,DC 在x與y方向上最大振幅值出現了“平臺期”,其“鎖定區域”圖形類似于梯形,在Ur=7 與8 時結構會發生最大振幅,如圖4(a)所示.剪切來流工況下(k=0.05),頻率比較小時(r=1.0,1.5)DC 在橫流向上的振幅值隨Ur的增大規則的增大,然而在r=2.0 工況下,Ymax/D在Ur≤7 時緩慢的增加,但當Ur=8 時,Ymax/D會從0.5(Ur=7)跳躍到1.47(Ur=8),DC 在此頻率比工況振幅啟動開關要晚于另外兩個頻率比工況,如圖4(b) 所示.由圖5 可觀察到,在r=1.5 工況下,DC 在Ur=7 與Ur=8 時尾部的負壓面積相當,如圖5(b)所示,使得DC 在橫流向上的振幅相同,出現了“平臺期”.然而,在r=2.0 工況下,DC 在Ur=7 時尾部負壓區面積接近于0,當折減速度增長到8 時,其尾部負壓區面積增大并超過了其他頻率比工況,導致結構大振幅現象會延時出現.當剪切率進一步增大到k=0.1 時,UC 在小頻率比工況下(r=1.0,1.5)橫流向振幅被完全鎖定的折減速度區間有所擴大(Ur=6～ 8),如圖4(c)所示.此時DC 在r=1.5 工況下無論是橫流向振幅還是順流向振幅都較平緩.當r=1.0 與r=2.0 時,其在橫流向上的振幅值在Ur≤7 時都較平緩,然而在Ur=8 處會突然跳躍到一個極大值,這與k=0.05 工況相似,但不同的是,在k=0.1 工況下,DC 在r=1.0 時Xmax/D最大會增長到0.5(Ur=8),結構順流方向振動會達到最大值.

圖4 不同頻率比與剪切率工況下,串列雙圓柱雙自由度最大振幅隨折減速度的變化(L/D=3.5)Fig.4 The variation of the maximum vibrating amplitude of tandem double cylinders with reduced velocity under different frequency ratios and shear rates in two degrees of freedom (L/D=3.5)

圖5 不同頻率比工況下,流場無量綱時均流場壓力圖(k=0.05)Fig.5 Dimensionless time-averaged pressure diagram of flow field at different frequency ratios (k=0.05)

3.1.3L/D=5.5

當間距比進一步增大到5.5 時,兩圓柱之間的間距超過臨界間距比,此時UC 的振動情況與單圓柱工況相似,而DC 受到上游圓柱尾流的影響明顯增強[12].圖6 給出了L/D=5.5 時不同剪切來流工況下UC 與DC 雙自由度振幅變化情況.由圖可觀察到UC 較DC 振幅變化更加規律,其振幅變化主要集中在4＜Ur＜9 范圍內.隨著剪切率的增大,不同固有頻率比對DC 影響較大,對UC 影響較小.這是由于對于串列雙圓柱繞流,上游圓柱的渦激振動是一種共振現象,然而下游圓柱受到共振作用的同時,還受到UC 尾流與圓柱的相互作用,隨著剪切率與間距比的增大,尾流與圓柱的相互作用逐漸起到主導作用,使得不同頻率比對圓柱振幅的影響越發明顯.Ur≤7時,DC 在r=2.0 工況下的Ymax/D值一直小于r=1.5 與r=1.0 工況.但是當Ur=8 時,r=2.0 工況下的橫流向最大振幅值會超過另兩個工況取得最大值,又會在Ur=9 時迅速減小.與均勻來流工況相比,DC 在剪切來流中振幅變化范圍有所擴大,在UC 尾流的影響下,DC 出現了次峰,且剪切率越大,UC 尾流與DC 相互作用越強,次峰越明顯,如圖6(b)與圖6(c)所示.相較于k=0.05 工況,剪切率增大到k=0.1 時,DC 在順流向的幅值變化呈波動狀,且頻率比越小波動越明顯.DC 在橫流向上,r=1.0 與r=2.0 工況均會在Ur=8 處取得極大值,然而r=1.5 工況則處于平穩的波動狀,沒有明顯的峰值,與L/D=3.5 工況類似,如圖4(c)所示.由于雙圓柱體結構間距較大,UC 受到DC 的影響較小,UC 尾渦脫落完整,DC 上行渦拉長在遠尾流區脫落,如圖7 所示.而下行渦由于DC 的劇烈振動受到抑制,在整個鎖定區間內,圓柱脫渦情況較為接近,使得此工況下圓柱振幅大小接近.

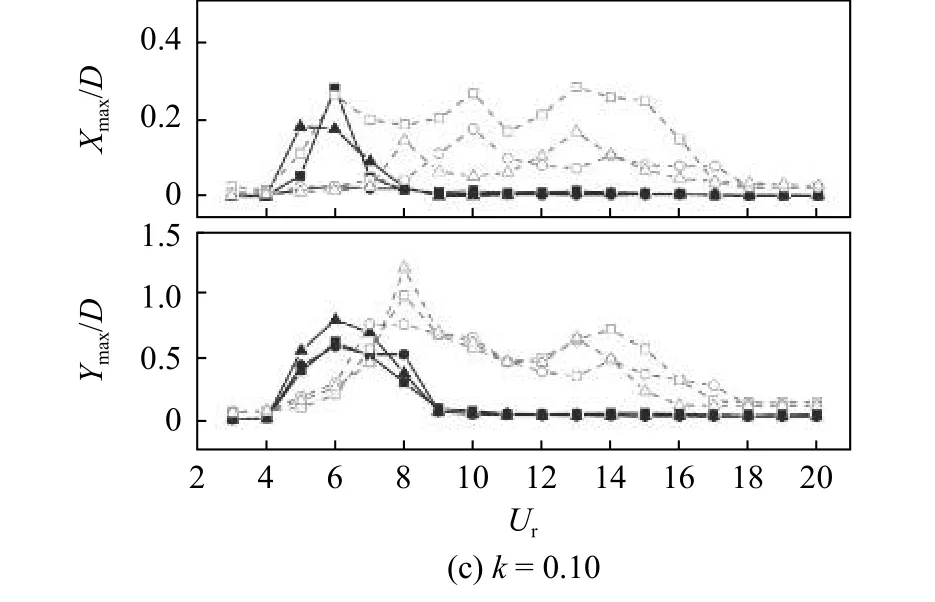
圖6 不同頻率比與剪切率工況下,串列雙圓柱雙自由度最大振幅隨折減速度的變化(L/D=5.5)Fig.6 The variation of the maximum vibrating amplitude of tandem double cylinders with reduced velocity under different frequency ratios and shear rates in two degrees of freedom (L/D=5.5)

圖7 r=1.5,k=0.1 時不同折減速度下的同一時刻流場瞬時渦量圖Fig.7 Instantaneous vorticity diagram of flow field at the same time at r=1.5 and k=0.1

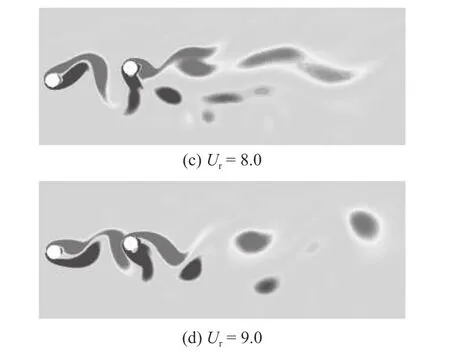
圖7 r=1.5,k=0.1 時不同折減速度下的同一時刻流場瞬時渦量圖 (續)Fig.7 Instantaneous vorticity diagram of flow field at the same time at r=1.5 and k=0.1 (continued)

3.2 相位特性變化

圓柱渦激振動中升力與位移的相位差變化體現了流體力做功的正負.當結構的振動頻率接近渦脫落頻率時會發生同步現象,升力幅值突然變大并且其與結構位移間的相位會有180°的跳躍[29-31].

3.2.1L/D=2.5

當L/D=2.5 時,雙圓柱體結構升力與位移之間的相位差在折減速度Ur=3～ 6 時接近于零,如圖8 所示,說明此時圓柱結構在一個振動周期內能量凈傳輸量為零.隨著折減速度進一步增大,在Ur=6～ 9 區間內升力與位移之間的相位差完成了從同相到反相的轉變,相位從0°跳躍到180°,能量傳遞在此區間內變得復雜起來,并且這個轉變區間正對應著圓柱振幅鎖定區間,由此說明相位轉變與結構振動幅度有著密切的關系,如圖2 所示.整體來說,剪切率的改變對升力與位移相位差的影響不明顯,UC 與DC 僅在相位轉變區間(Ur=6～ 9)較為雜亂而在其它區間內都較為規則.當間距比較小時,UC 與DC 結合類似一個整體,在來流作用下,兩者之間的相位差呈現同步變化.另一方面,頻率比的變化對UC 與DC 的影響主要在于:在相位轉變區間,頻率比越小,結構升力與位移之間的相位差完成從同相到反相的轉變速度越快.然而,頻率比越大在鎖定區間圓柱振幅越大,如圖2 所示.由此可以總結出:隨頻率比的增大會逐漸加強對結構渦激振動效應的影響,能量從流體傳遞到柱體的速度越緩慢,且過程會更復雜.

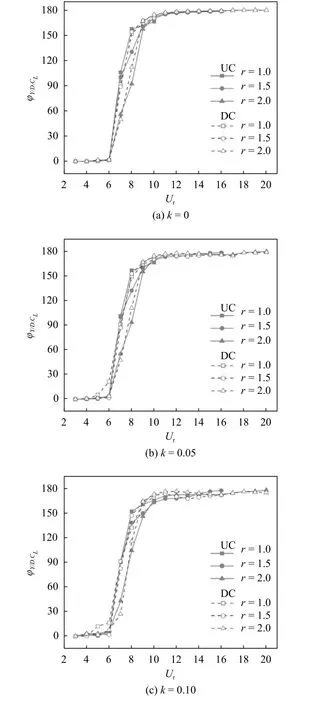
圖8 在不同剪切率與頻率比下,串列雙圓柱升力與橫流向位移相位差變化圖(L/D=2.5)Fig.8 Diagram of phase difference between lift and transverse displacement of double cylinders in series at different shear rate and frequency ratio (L/D=2.5)

以L/D=2.5,k=0.0,r=2.0 工況為例,當Ur=6,8,10 時,UC 上升力與位移間相位差分別處于同相、相位轉變以及反相區間.圖9 為3 個折減速度工況下升力時程曲線與位移時程曲線圖,由圖9(a)可知,當Ur=6 時,升力與位移同相變化,升力時程曲線變化幅值明顯大于位移時程曲線,且橫流向位移時程曲線變化呈現標準的正弦曲線而升力位移時程曲線雖然同為正弦曲線,但其每一個峰值由一大一小兩個次峰組成.當Ur=8 時,升力與位移處于相位轉變的復雜期,升力時程曲線呈現明顯的調制振幅,橫流向時程曲線雖為調制振幅但在各個瞬時階段總的振幅值相差不大,且位移幅值變化區間要大于升力時程曲線,如圖9(b)所示.當Ur=10 時,升力與位移完成了相位轉變,升力時程曲線與位移時程曲線反相且均會呈現規則的正弦曲線,升力變化幅值區間再次大于橫流向位移變化幅值區間.由此可以總結出:升力與位移時程曲線在同相與反相區間會呈規則的正弦曲線,然而在相位轉變期間,能量傳遞紊亂,升力與位移時程曲線均會發生調制振動.

圖9 在Ur=6,8,10 時,上游圓柱升力與橫流向位移時程曲線圖(k=0.0,r=2.0)Fig.9 The time history curve of lift force and transverse displacement of upstream cylinder at Ur=6,8 and 10 (k=0.0,r=2.0)

3.2.2L/D=3.5

當間距比L/D=3.5 時,隨著兩圓柱之間間隙的增大,上游圓柱的尾流將對下游圓柱造成一定的影響.如圖10 所示,在均勻來流工況下,UC 與DC 上升力與位移相位差的轉變與L/D=2.5 工況相似,都主要在“鎖定區間”完成相位的轉變.剪切來流下UC 在Ur=4 處出現了“弱鎖定”現象,特殊的是隨著剪切率增大到0.1 時,UC 與DC 在相位轉變區間(Ur=7～ 8)出現了“平臺期”,在這個“平臺期”內,隨折減速度的變大,升力與位移相位差不發生改變,流體與柱體之間能量傳遞相同.如圖10(c)所示,“平臺期”僅出現在r=1.5 與r=2.0 工況中,UC 在此兩個頻率比的相位差接近而DC 隨頻率比的增大升力與位移的相位差增大.通過對“平臺期”附近折減速度工況進行加算發現從Ur=6 增長到Ur=7 的過程中,各工況呈規律的線性增長,而從Ur=8 增長到Ur=9的過程中,會在Ur=8 處出現跳躍增長.較為特殊的是,在小頻率比r=1.0 時,UC 相位差會從40°跳躍到120°,而DC 相位差的變化較小,Ur=7 與Ur=8兩個工況的相位差幾乎一致.

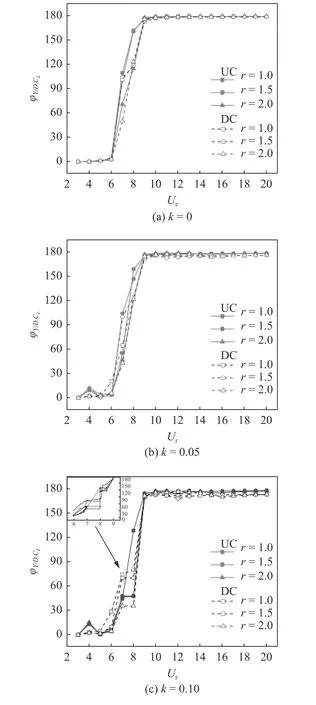
圖10 在不同剪切率與頻率比下,串列雙圓柱升力與橫流向位移相位差變化圖(L/D=3.5)Fig.10 Diagram of phase difference between lift and transverse displacement of double cylinders in series at different shear rate and frequency ratio (L/D=3.5)

以L/D=3.5,k=0.1 工況為例,DC 橫流向振幅在Ur=8 時取得最大值,結構進入“鎖定狀態”發生共振現象.圖11 給出了不同頻率比工況下DC 在共振狀態的升力時程曲線與位移時程曲線.當r=1.0 時,升力與橫流向位移時程曲線均為調制振幅,且橫流向位移時程曲線呈現為更為特殊的“拍”頻.當升力曲線幅值達到最大值時,位移曲線幅值則達到最小值,兩者之間會發生錯位振動.當r=1.5 時,升力與位移時程曲線調制幅度變小,時程曲線變化情況越發規律,位移時程曲線幅度明顯要大于升力時程曲線.當頻率比進一步增大到2.0 時,橫流向位移時程曲線已恢復成規律的正弦曲線,而升力時程曲線則呈現一個大周期包含3 個小周期的特殊調制振幅.

圖11 在不同頻率比工況下,下游圓柱升力與橫流向位移時程曲線圖(k=0.1,Ur=8)Fig.11 The time history curve of lift force and transverse displacement of downstream cylinder at Ur=6,8 and 10 (k=0.1, Ur=8)

3.2.3L/D=5.5

當間距比進一步增大到5.5 時,此時兩圓柱之間的距離超過了臨界間距比,上游圓柱與來流之間的相互作用類似于單圓柱體,而下游圓柱既受到來流作用,又受到上游圓柱尾流的干擾,使得其橫流向位移與升力相位差隨折減速度的變化越發復雜.由圖12 可知剪切率的不同對UC 影響較小而對DC 影響較大.均勻來流工況下,如圖12(a) 所示,UC 上升力與位移間的相位差變化較為規律,主要在“鎖定區間”完成了相位的轉變,且頻率比越大,轉變的速度越緩慢.DC 的不同之處是:當Ur=8 時,DC 升力與位移相位差增長到150°附近,而在Ur=9處相位差跌落到120°出現了能量的“反哺”,隨著折減速度的增大又再次回到180°.在剪切來流當中,當折減速度較小時(Ur=3),上下兩圓柱存在30°的初始相位差,隨著Ur的增大,升力與位移間的相位差先減小到0°隨后在“鎖定區間”(Ur=6～ 8)完成從同相到反相的轉變.特別的是,當DC 退出“鎖定區間”后,在Ur=9 處,升力與位移間的相位差會從180°減小到120°左右,最后再隨折減速度的增大又重新回到180°.從圖12(b)與圖12(c)可以觀察到,剪切率越大(k=0.1),下游圓柱相位差重新回到180°的折減速度越大.當k=0.05 時,r=1.5 與r=2.0 工況下的DC 相位差變化同步,不同的是r=1.0 工況下的相位差在小幅度上升后又會在Ur=11 處降低到120°左右,最后在Ur=16 處徹底完成相位的轉變.當剪切率增大到1.0 時,UC 與DC 僅在r=1.5 頻率比工況下出現了“平臺期”.對于上游圓柱而言,當Ur≥9 時,3 個頻率比工況均已完成相位的轉變,但特殊的是r=1.0 工況較另兩個頻率比工況要更加不穩定.對于下游圓柱,當Ur=8 時,3 個頻率比工況相位差值較大,r=1.0 與r=2.0 工況均是在到達一個極大值后在Ur=9 時相位差值回落且隨著折減速度的增大最后在較大折減速度下重新上升到180°.然而,對于r=1.5 工況沒有出現相位差回落現象,其升力與位移間的相位差隨著折減速度的增大緩慢增長,并最終在Ur=18 時徹底完成相位的轉變.

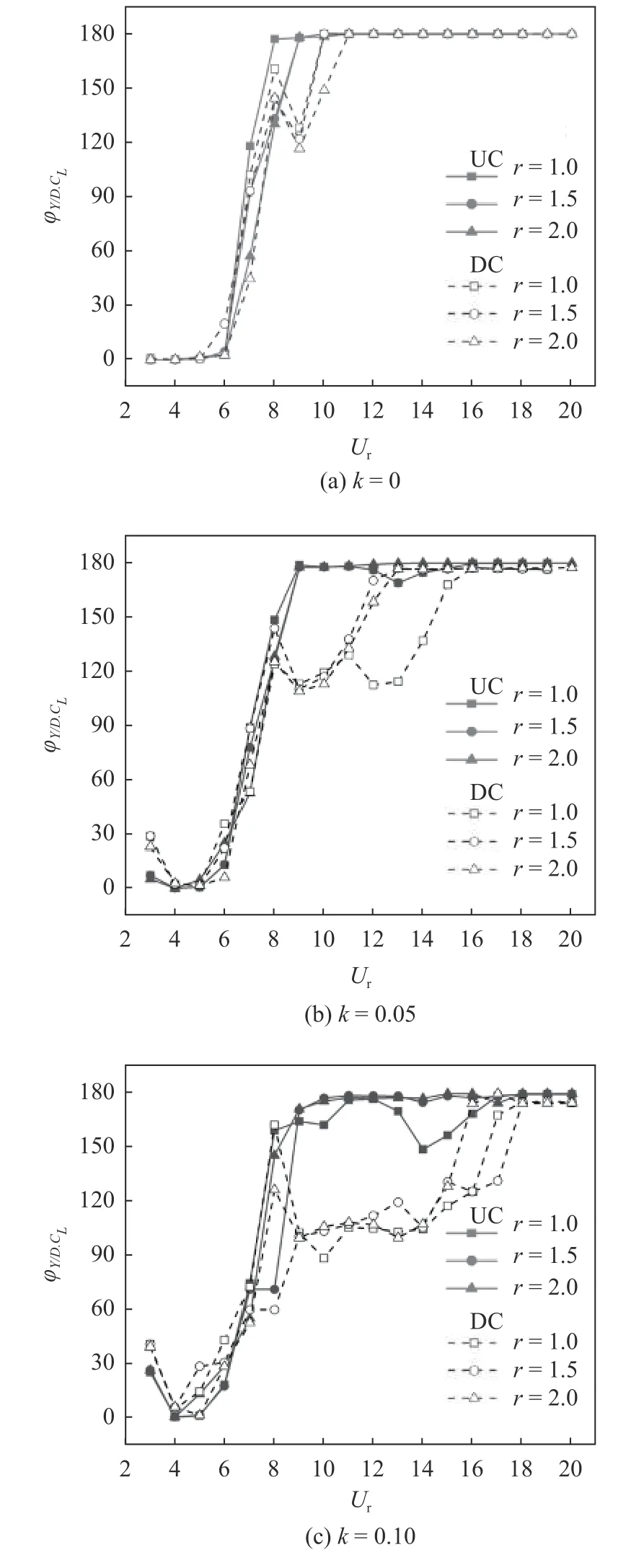
圖12 在不同剪切率與頻率比下,串列雙圓柱升力與橫流向位移相位差變化圖(L/D=5.5)Fig.12 Diagram of phase difference between lift and transverse displacement of double cylinders in series at different shear rate and frequency ratio (L/D=5.5)

由圖12(c) 可觀察到當圓柱退出鎖定區間后,UC 在Ur=8 處完成相位轉變后,隨著折減速度的增大,將會一直維持反相變化.圖13 給出了L/D=5.5,k=0.1,r=1.0,Ur=14 工況UC 與DC 的升力時程曲線與橫流向位移時程曲線圖.由圖13(a) 可知,UC 的橫流向位移時程曲線為一個大周期包含兩個小周期的調制振幅,而升力時程曲線變化類似于正弦曲線,但每臨近兩個峰值幅值有細小的差別.另一方面,DC 升力時程曲線呈現特殊的調制振幅,波峰變化相同,而波谷則為一低一高兩種波況,且兩者之間最小振幅值為接近1.7 倍大小的關系,如圖13(b)所示.

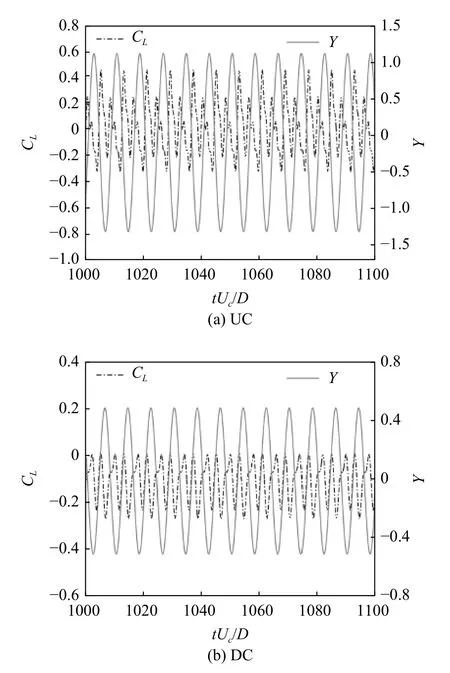
圖13 Ur=14 時,串列雙圓柱升力與橫流向位移時程曲線圖(k=0.1,r=1.0)Fig.13 The time history curve of lift force and transverse displacement of upstream cylinder and downstream cylinder at Ur=14 (k=0.1, r=1.0)

3.3 流體力功率譜密度分析

在3.2 節中通過對串列雙圓柱的升力與橫流向位移相位差變化情況進行對比分析,探究了不同工況下圓柱結構與流體之間能量轉換的關系.本節將以r=1.5 工況為例進一步對下游圓柱流體力系數功率譜密度(PSD)在不同間距比以及剪切率工況下的主峰幅值、頻譜成分及波動性進行分析,深入探究結構能量變化情況及內在力學機理.

如圖14 所示,在均勻來流工況下,當Ur=4 時,不同工況下的升阻力PSD 曲線均較為光滑,主頻能量值較小,圓柱振動微弱.當折減速度增長到6 時,在小間距比工況下(L/D≤3.5)流體力PSD 曲線增大至3 階,升力PSD 曲線包圍的面積有效增大使得DC 獲得更多的動能,在橫流向開始產生較大的振幅.然而,在L/D=5.5 工況下,流體力系數PSD 曲線次峰及雜頻占據的能量值增多,下游圓柱運動更加復雜.當Ur為7～ 8 時,此時下游圓柱位于鎖定區間,PSD 曲線出現多階同等量級的頻率峰值,波動性增強,能量由流體大量流向圓柱體,DC 劇烈振動.當Ur增大到9 時,在L/D≤3.5 工況下,下游圓柱流體力PSD 曲線波動性減弱,能量已基本完成從流體傳入結構物的轉變.然而在L/D=5.5 工況下,流體力PSD 曲線出現了多個雜頻,且能量均勻分布在各雜頻上,使得能量出現“反哺”現象,能量會從結構傳回到流體中,如圖12 所示.

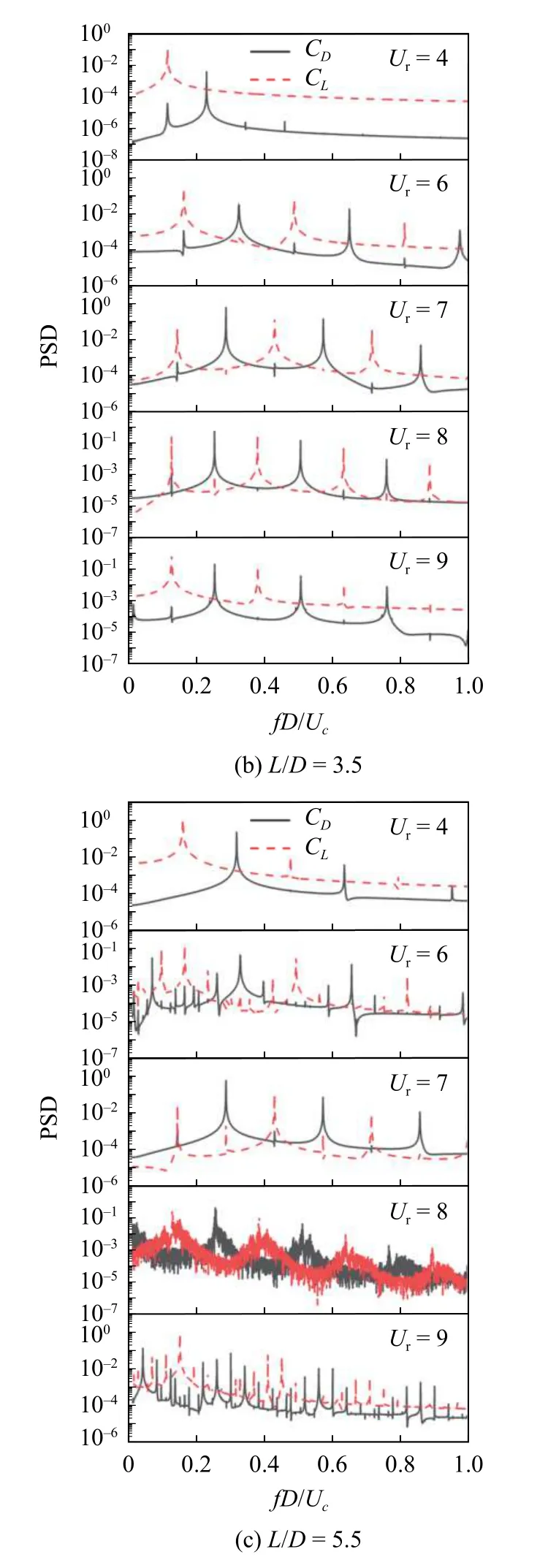
圖14 不同間距比工況下,下游圓柱升力系數功率譜密度(紅線)與阻力系數功率譜密度(黑線) (k=0.0,r=1.5)Fig.14 The power spectral density of lift coefficient (red) and drag coefficient (black) of downstream cylinder under different spacing ratios (k=0.0,r=1.5)

與均勻來流相比,剪切來流工況下,各工況流體力PSD 曲線波動性增強,所包含的多階頻率峰值增多,能量變化劇烈相對應的下游圓柱振動情況越發劇烈,如圖15 所示.在Ur=4 工況下,升力PSD 曲線與阻力PSD 曲線主峰頻率重合,使得能量大量由流體傳入圓柱體結構,在升力與橫流向相位差圖中出現了“弱鎖定”現象.隨折減速度的增大(Ur≤8),升力系數PSD 曲線出現的次峰數目增多且構成整體呈下降趨勢的曲線,包含的總能量較多,DC 逐漸進入鎖定狀態并振動劇烈.值得注意的是,當L/D≥3.5 時,如圖15(b)與15(c)所示,Ur=7 與Ur=8 工況下流體力系數PSD 曲線出現的頻率峰值數目、整體曲線變化趨勢以及各階頻率峰值所對應的能量值都相同.從圖16 觀察到,此時兩個折減速度工況在一個周期內的能量變化曲線其高、低峰值以及曲線變化形態都相同,這就意味著折減速度從7 增至8 的過程中圓柱能量變化相同,這可能是升力與橫流向位移相位差出現“平臺期”的原因,如圖10(c)與圖12(c)所示.

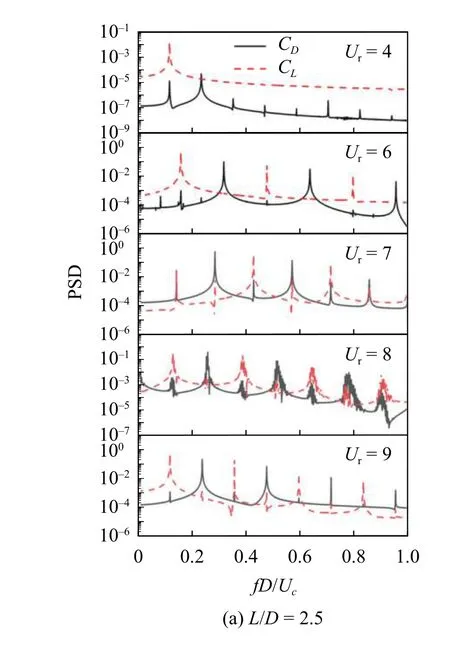
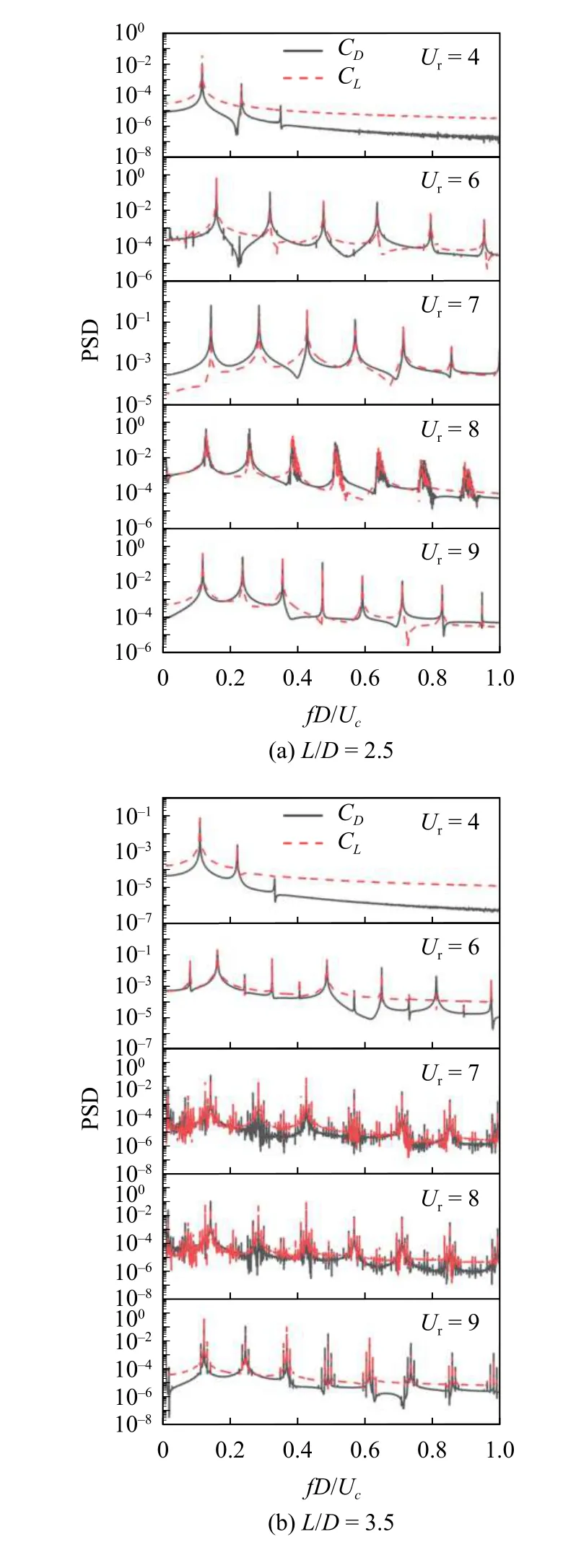
圖15 不同間距比工況下,下游圓柱升力系數功率譜密度(紅線)與阻力系數功率譜密度(黑線) (k=0.1,r=1.5)Fig.15 The power spectral density of lift coefficient (red) and drag coefficient (black) of downstream cylinder under different spacing ratios(k=0.1,r=1.5)

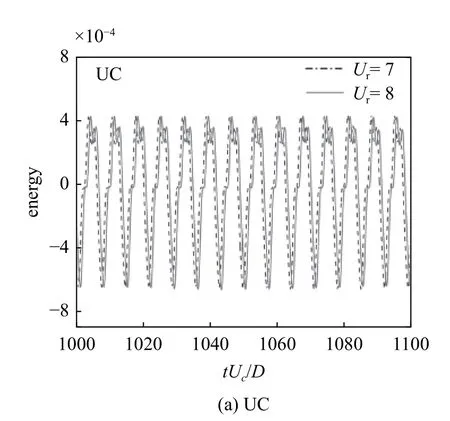
圖16 在Ur=7 與Ur=8 工況下串列雙圓柱的能量曲線(L/D=3.5,k=0.1,r=1.5)Fig.16 Energy curve of tandem double cylinders under the of Ur=7 and Ur=8 cases (L/D=3.5,k=0.1,r=1.5)

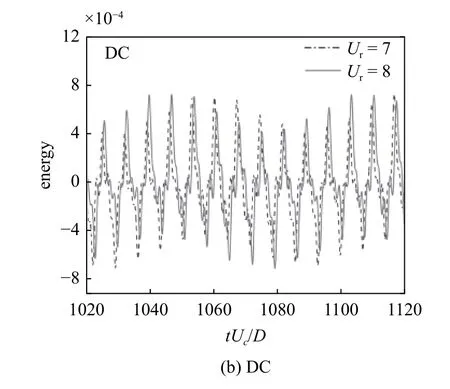
圖16 在Ur=7 與Ur=8 工況下串列雙圓柱的能量曲線(L/D=3.5,k=0.1,r=1.5) (續)Fig.16 Energy curve of tandem double cylinders under the of Ur=7 and Ur=8 cases (L/D=3.5,k=0.1,r=1.5) (continued)

4 結論

基于四步半隱式特征線分裂算子有限元方法,對串列布置雙圓柱雙自由度結構體系渦激振動問題進行了數值模擬,分析了間距比、剪切率、頻率比以及折減速度四個關鍵影響因素的變化對結構振動響應及流場的影響,主要結論如下.

(1)UC 的共振區間明顯寬于DC 的共振區間,UC 在兩個自由度方向達到最大值的折減速度不同,而DC 基本同步.由于來流與間隙流的干擾,使得UC 與DC“鎖定區間”的折減速度范圍存在差值,UC 較DC 更早進入也更早退出共振狀態.固有頻率比與剪切來流的變化對DC 影響較大,對UC 影響較小.

(2)兩圓柱主要在鎖定區間完成相位的轉變.頻率比越大對圓柱渦激振動影響越大,能量從流體傳遞到柱體的速度越緩慢與復雜,圓柱完成從同相到反相的速度越緩慢.特別的是,在L/D≥3.5,r≥1.5的剪切來流工況下會出現相位差的“平臺期”.此“平臺期”出現在鎖定區間Ur=7 與Ur=8 工況下,此時隨著折減速度的增大,升力與位移之間的相位差不變.當間距比超過臨界值時,對DC 相位轉變影響較大,下游圓柱在完成相位轉變后會隨著折減速度的增大出現相位差回落現象,并且剪切率越大,回落的折減速度區間越廣.

(3)在均勻來流工況下,升阻力PSD 曲線頻率呈兩倍關系,然而在剪切來流工況下,則基本重合.當間距比較大時,折減速度越大,流體力PSD 曲線出現的雜頻越多,由于能量均勻分布在各雜頻上,使得能量出現“反哺”現象.在剪切來流工況下,當L/D≥3.5 時,Ur=7 與Ur=8 工況中流體力系數PSD 曲線高度相似,同時兩工況的能量變化也相同,這可能是在升力與位移相位差圖中出現“平臺期”的原因.