含分數階Bingham 模型的阻尼減振系統時滯半主動控制1)

張婉潔 *, 牛江川 *,, 申永軍 *, 楊紹普 *, 劉佳琪

*(石家莊鐵道大學交通工程結構力學行為與系統安全國家重點實驗室,石家莊 050043)

? (石家莊鐵道大學機械工程學院,石家莊 050043)

引言

半主動控制系統[1-4]具有控制簡單易操作,以及良好的控制效果等特點,在許多工程領域得到了廣泛應用,如車輛懸架[5-6]、船舶可控浮閥[7]、結構振動控制[8]等.半主動控制策略的“開-關”切換條件中,通常需要采集系統的位移、速度等狀態反饋信息進行規則判斷,從而調整控制系統的阻尼、剛度以實現切換控制.

磁流變液阻尼器(magnetorheological fluid damper,MRFD)是一種典型的半主動控制裝置,通過調整控制電流利用磁流變液提供可控阻尼力,有效地實現振動控制[9-10].常用的描述磁流變液阻尼器的模型主要包括Bingham 模型、雙曲正切模型、Bouc-Wen 模型、黏性Dahl 模型和代數模型等[11-12].而基于分數階的Bingham 模型已被證明能夠以較少的參數更準確的描述磁流變液阻尼器的動力學特性,不但能夠擬合磁流變液阻尼器力-位移間的響應關系,并且可以更準確地描述其速度-阻尼力的滯回特性[13-15].

對于基于磁流變液阻尼器的受控系統而言,傳感測量、信號傳遞及作動機構執行均需要一定的時間,從而導致控制回路出現無法避免的時滯[16].時滯系統表現為系統輸出相對于系統的輸入具有一定的延遲,由于時滯的存在,可能會使系統的動態性能變差,降低控制系統的控制效果,甚至導致系統不穩定[17];也可能會改善系統的控制效果.王在華和胡海巖[18]從動力學角度對時滯動力系統的特點、研究方法、動力學等熱點研究進展問題進行了綜述.徐鑒等[19-20]深入討論了時滯耦合系統的動力學研究進展.Yu 等[21]對天棚控制下磁流變阻尼器中的非線性和時滯特性進行了分析,得到了不同非線性和時滯參數下系統的分岔準則.Shen 和Ahmadian[22]分析了4 種含時滯的半主動動力吸振器的非線性動力學特性,以及時滯對控制系統性能的影響.Yan 等[23]分析了二自由度車輛懸架系統在時滯最優控制下的性能,并討論了時滯對主動懸架系統控制穩定性的影響.Pyragas 等[24-26]提出的時滯狀態反饋已成為有效調控系統性能的重要途徑.Sun 和Xu[27]分析了一種二自由度的含時滯的可控機械吸振裝置,實現了時滯反饋控制.Naik 和Singru 等[28]研究了時滯反饋控制下1/4 車輛懸架模型的共振、穩定性以及混沌振動問題.Taffo 等[29]分析了小時滯反饋控制下二自由度非線性車輛懸架的穩定性切換與分岔問題.Sun 等[30-31]分別提出了一種新型的時滯耦合非線性隔振-吸振復合結構,可有效抑制系統的共振,并分析了非線性隔振系統在多種不同激勵下時滯主動控制的最優參數.

目前,大多數時滯減振控制策略是將含有時滯的位移、速度或加速度等反饋物理量直接引入系統的動力學方程.而當作動器的作用與時滯反饋物理量無關時,時滯對半主動控制的影響還需要進一步研究.因此,本文針對半主動控制過程中不可避免的時滯問題,在控制切換條件中引入時滯,將時滯作為一個可控變量,基于含有分數階Bingham 模型的磁流變液阻尼器的線性剛度系統,構建含時滯的半主動控制系統模型.利用平均法對系統的主共振響應進行解析研究,采用Lyapunov 理論分析系統的穩定特性,并詳細分析時滯對半主動阻尼控制隔振系統振動特性的影響.

1 近似解析解

基于磁流變液阻尼器的半主動阻尼控制隔振系統的物理模型如圖1 所示,其中磁流變液阻尼器的阻尼力采用分數階Bingham 模型進行描述.

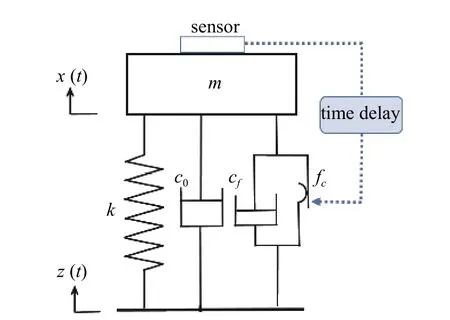
圖1 半主動阻尼控制隔振系統模型Fig.1 Model of semi-active damping on-off vibration isolation system

根據牛頓定律得到運動學方程為

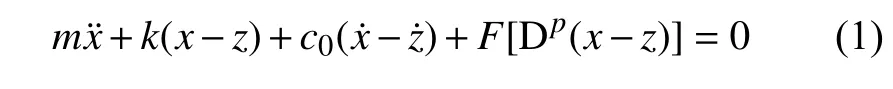
其中,磁流變液阻尼器的阻尼力為

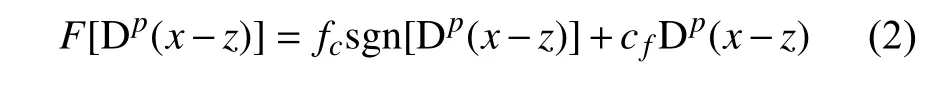
式中,fc為可變庫倫阻尼力,與磁流變液的剪切屈服強度成正比,通過輸入電壓或電流改變磁場強度進行調節;c0為系統的等效黏性阻尼系數,cf為磁流變液阻尼器的黏性阻尼系數,由其制造尺寸和磁流變液的黏度系數決定.Dp(x-z)表示位移差的p階導數,且 0＜p≤1 .依據Gerasimov-Caputo 定義[32],分數階微分項可以表示為

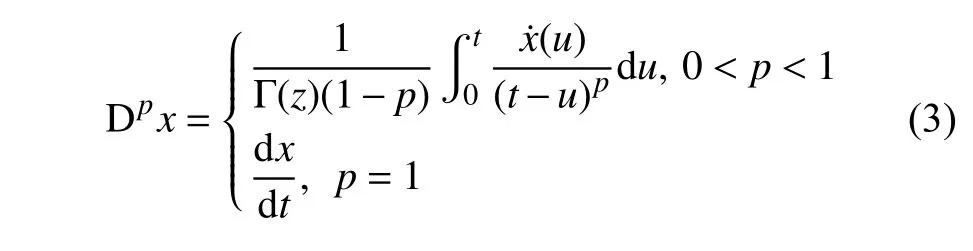
其中,Γ(z)為Gamma 函數,滿足 Γ(z+1)=zΓ(z) .

選取簡諧激勵z=Bcos(ωt) 作為基礎激勵,其中,B為簡諧激勵的幅值,且為常數,ω 為簡諧外激勵的角頻率.令y=x-z,代入式(1)可得

依據平均法,設式(5)的解滿足

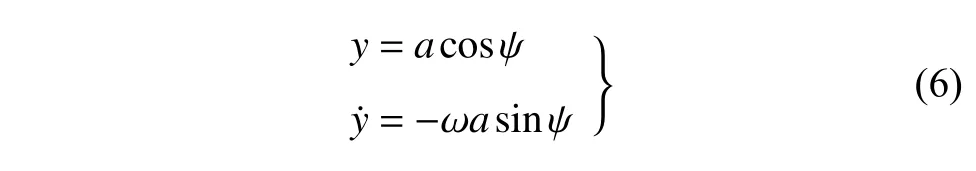
其中,ψ=ωt+φ .根據平均法可得到一階近似解振幅和相位滿足的方程

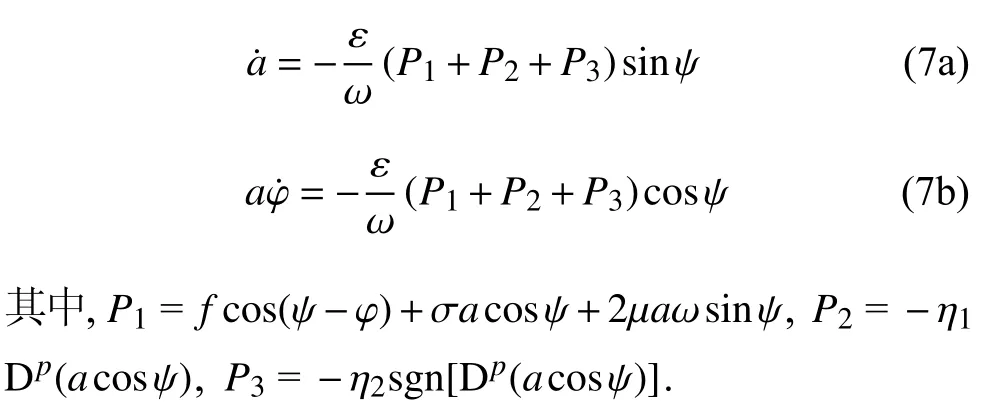
由于振幅和相位是隨時間變化的 ε 的同階小量,因此將式(7a)和式(7b)在一個周期內進行平均處理,得到近似解析解振幅和相位的顯式,即有

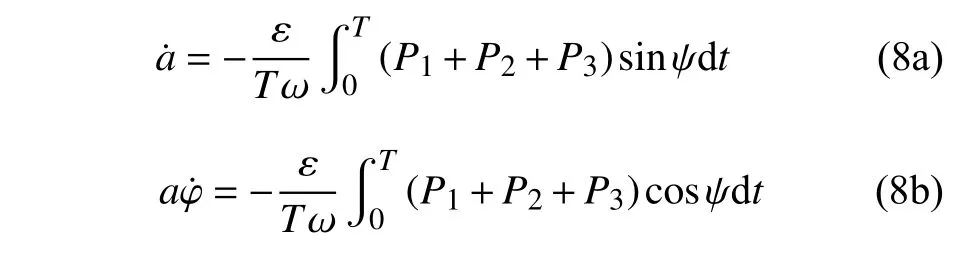
采用天棚阻尼半主動控制策略[33-35]對基于磁流變液阻尼器的隔振系統進行阻尼控制,磁流變液阻尼器所提供的阻尼力可表示為

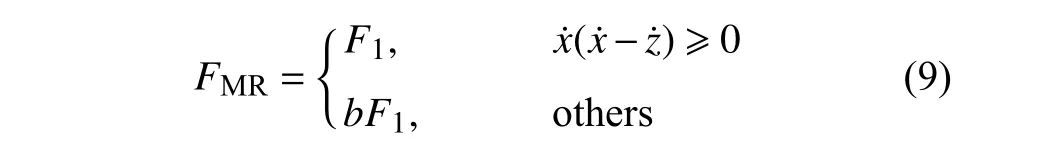
其中,b為半主動控制參數(0≤b≤1),F1為磁流變液阻尼器所能提供的最大阻尼力.考慮到磁流變液阻尼器在電壓為零時仍可提供一定的阻尼力,因此設定b=0.1 .

然而,基于磁流變液阻尼器的半主動控制系統在信號采集、信號傳輸、控制器決策、磁流變液阻尼器的響應過程中,存在的時滯會造成半主動控制信號滯后于理想狀態.當采用半主動控制策略,系統在進行相應動作執行切換時,可控阻尼力FMR與當前時刻的系統速度x˙(t) 同步.而由于實現目標的控制系統和作動機構均需要一定的反應時間,具有時間滯后量 τ＞0,使得控制判斷條件并非與當前時刻的速度(t) 同步,而是依賴于之前從傳感器中獲得的參數,與前面某一時刻的速度(t-τ) 同步.基于磁流變液阻尼器隔振系統的時滯半主動控制流程如圖2所示.

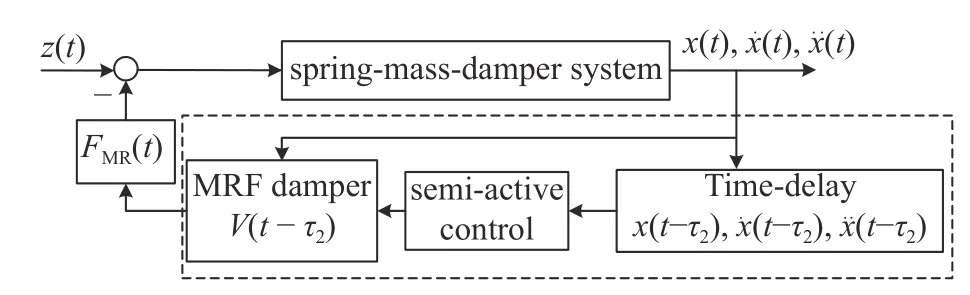
圖2 基于磁流變液阻尼器隔振系統的時滯半主動控制流程圖Fig.2 Flow chart of the semi-active control of the MRFD based vibration isolation system with time delay

將系統中的時滯綜合表示為時滯 τ,含時滯的天棚阻尼控制策略如下

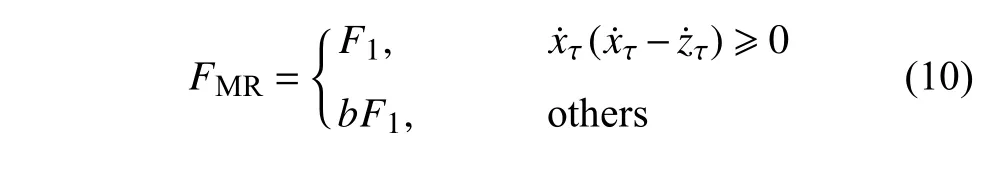
其中xτ=x(t-τ),zτ=z(t-τ) .控制條件為

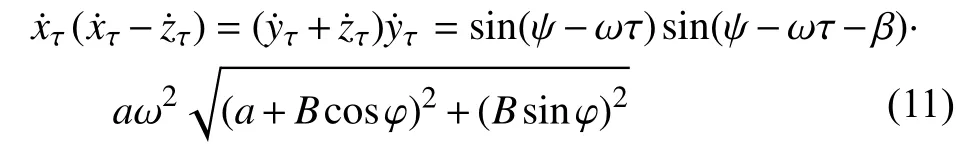
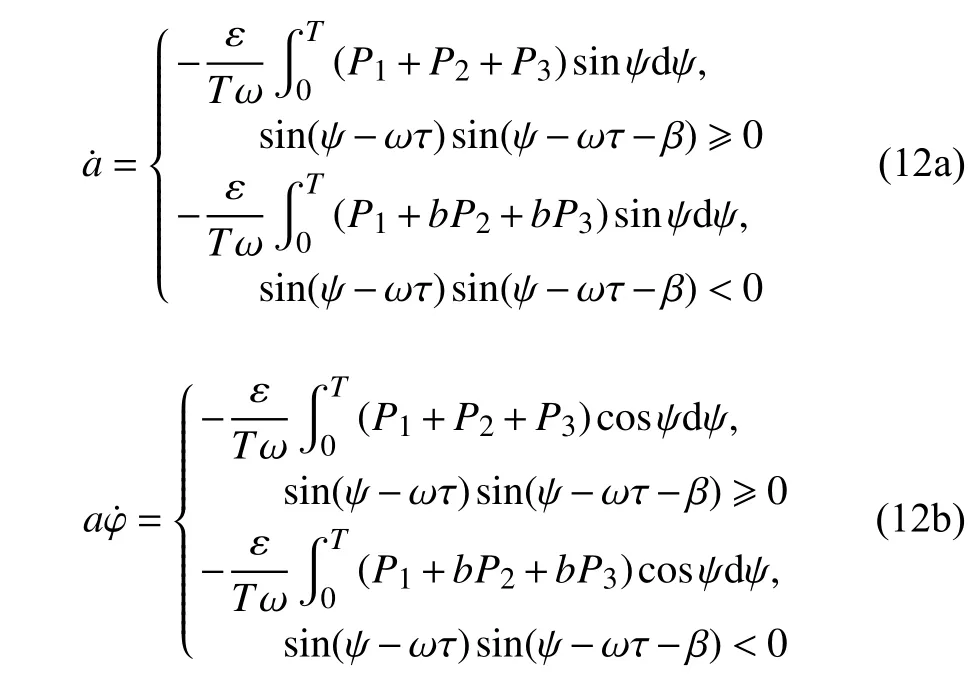
對于周期函數,其周期為T=2π/ω,式(8a)和式(8b)中第一部分的積分為

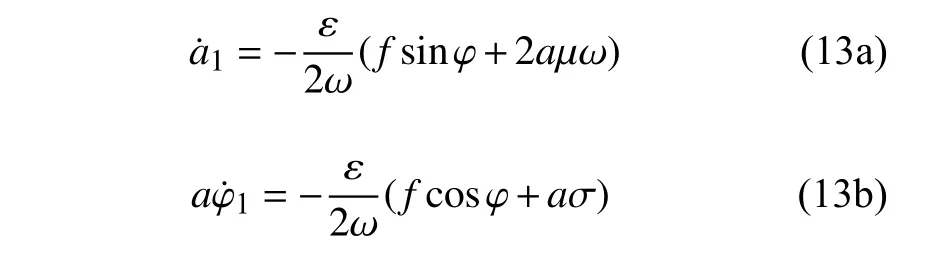
根據文獻[36-37],可以得到穩態響應時分數階項的近似表示

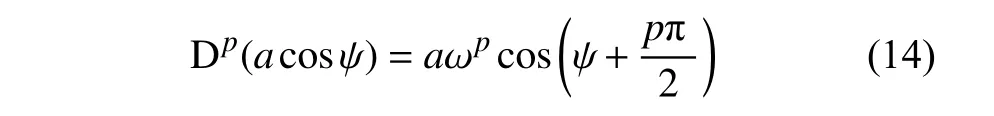
因此,第二部分在一個周期內的積分可以為:

當β ≥0 時

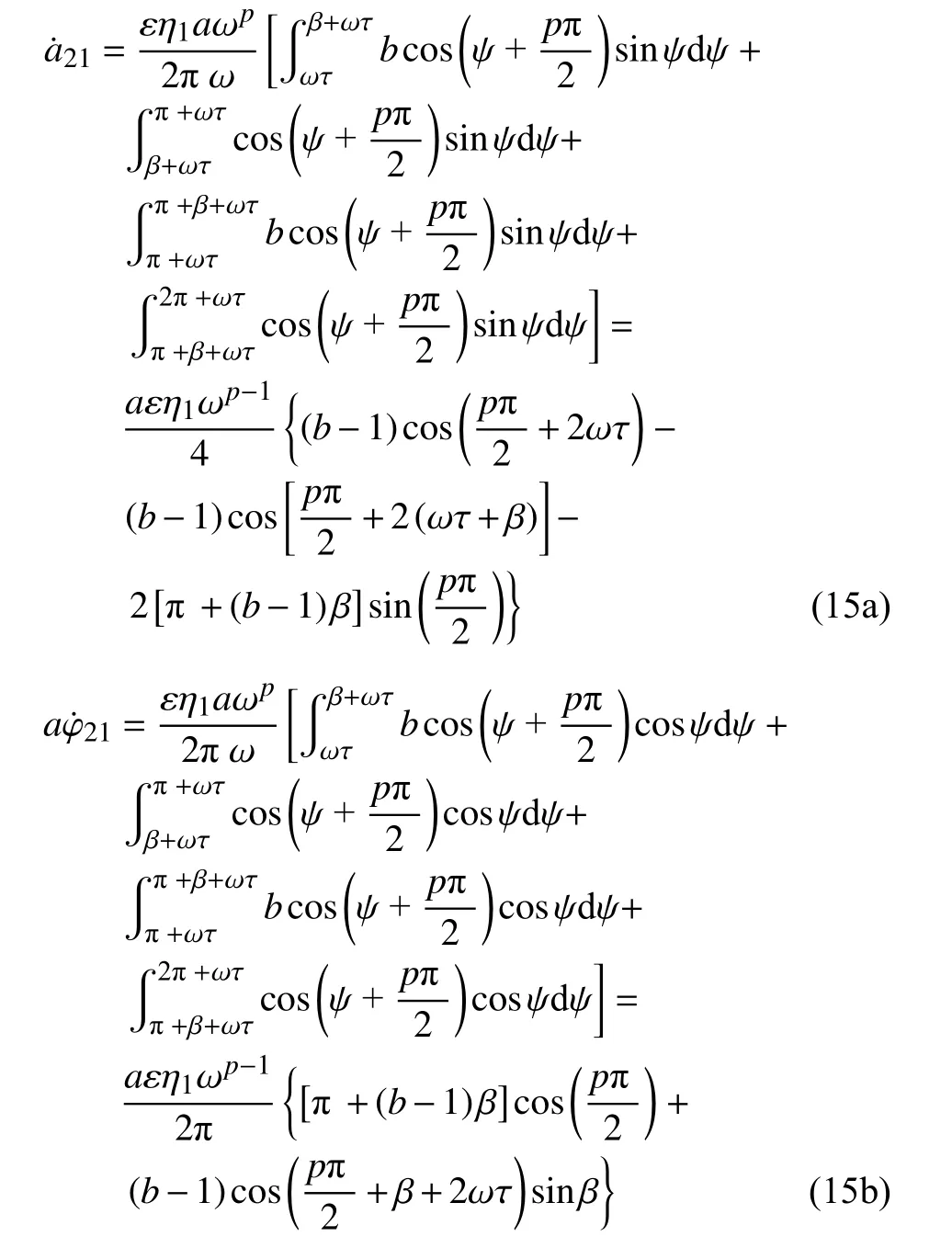
當β ＜0 時計算類似,由此可以得到第二部分在一個周期內的積分為

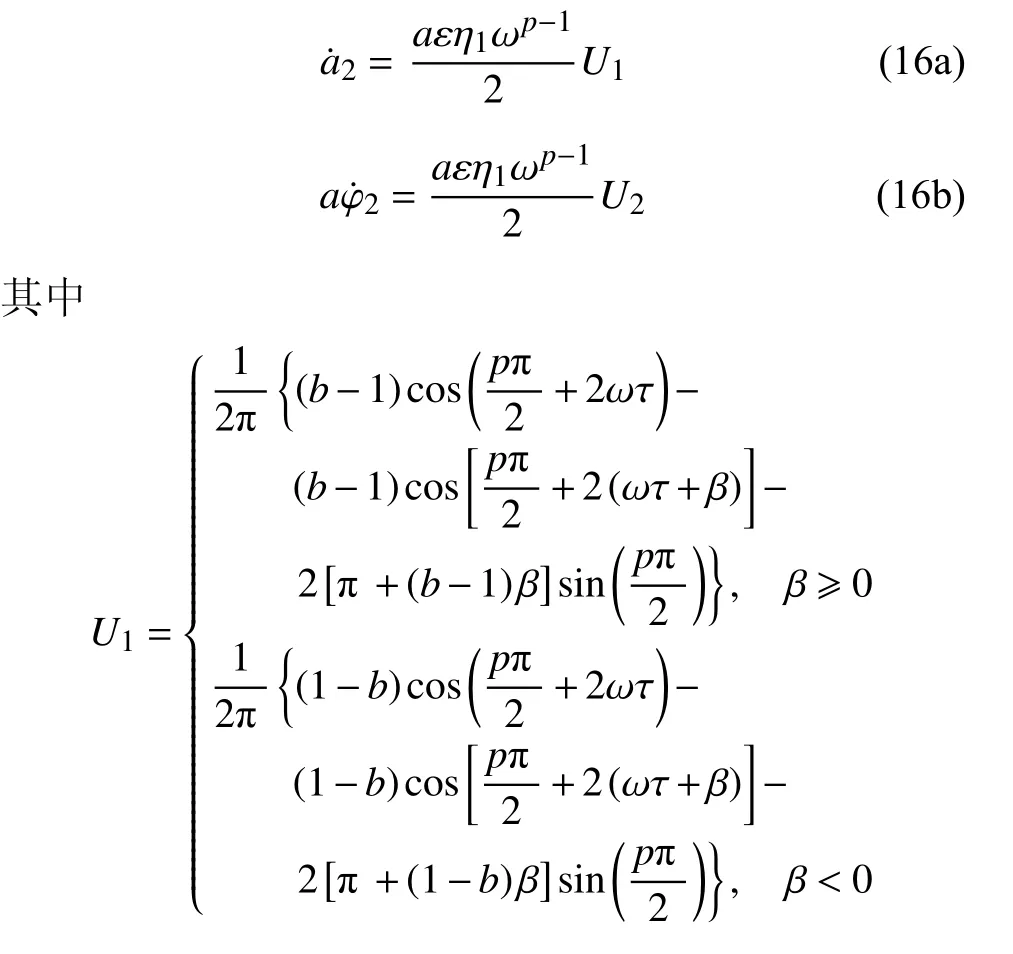
當考慮時滯對半主動控制的影響時,計算第3 部分在一個周期內的積分需要分別考慮8 種情況.當β ≥0 時,包括如下4 種情況:情況(1) (記作q1)

情況(3) (記作q3)

情況(4) (記作q4)

當β ＜0 時,同樣包含4 種情況:

情況(5) (記作q5)

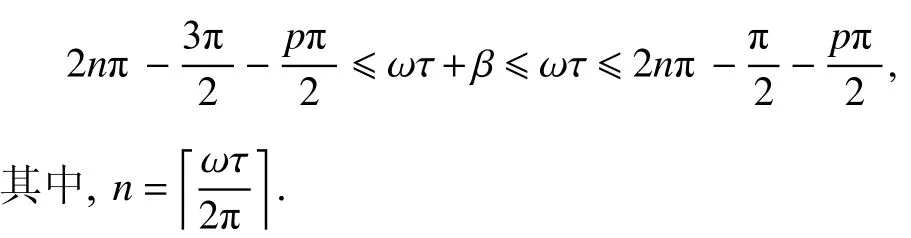
情況(6) (記作q6)

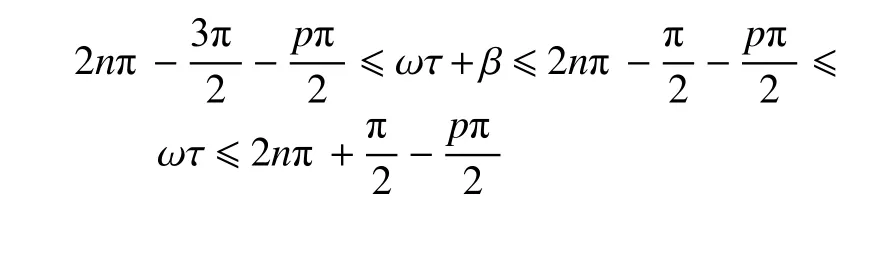
情況(7) (記作q7)

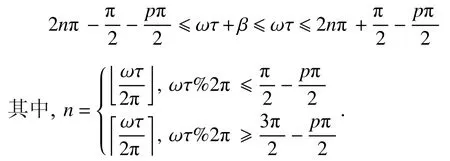
情況(8) (記作q8)

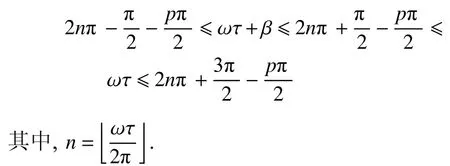
假設a＞ 0,在情況(1)下計算和可以得到

其他情況下可以進行類似的計算.由此可以得到第3 部分在一個周期內的積分為

其中

可以看出U和V既與控制參數b有關,又與時滯τ有關.因此,當β≥0和β＜0時,a˙和aφ˙可統一表示為

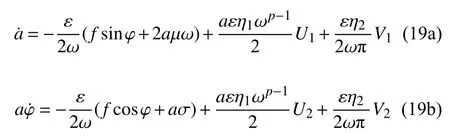
將系統原參數代入可得

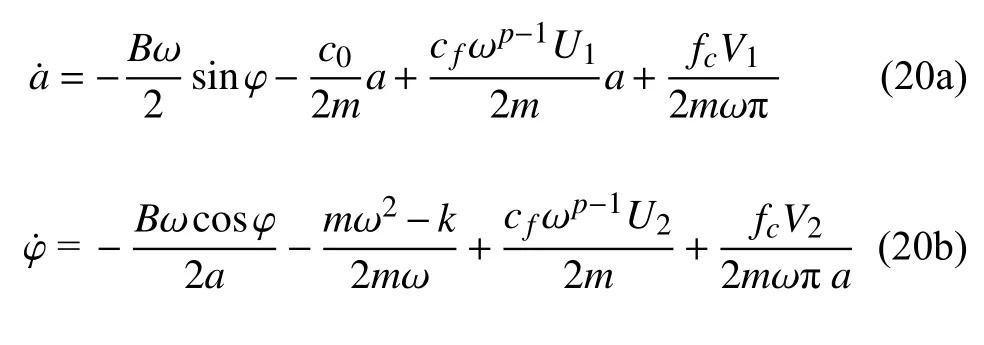
2 系統的定常解

研究系統的定常解,假設和分別是穩態解對應的振幅和相位,令式(20a)和式(20b)中=0,=0,可以得到系統的穩態方程

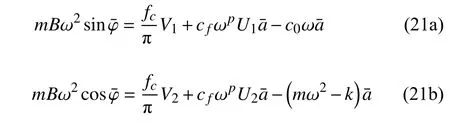
依據式(21a)和式(21b)可以得到系統的穩態幅頻響應方程為

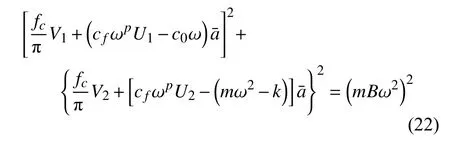
以及相頻響應方程

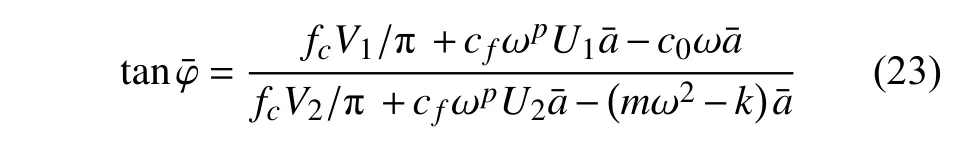
根據幅頻響應方程可以得到

3 定常解的穩定性分析

采用Lyapunov 一次近似理論判斷系統的穩定性,對穩態解引入小擾動,令a=+Δa,φ=+Δφ,代入式(20a) 和式(20b),略去高階項進行線性化,可得

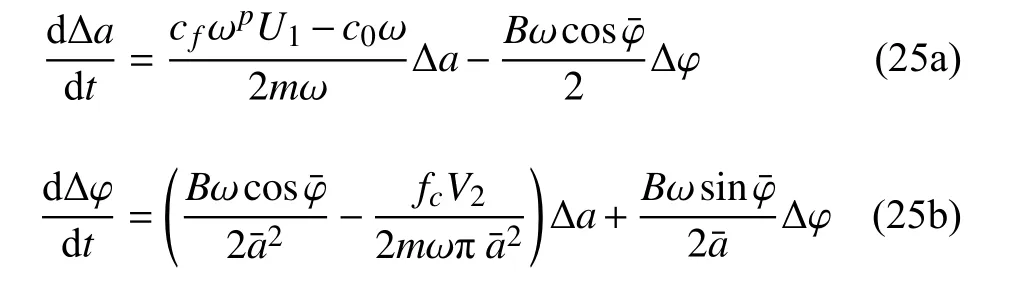
則特征方程為

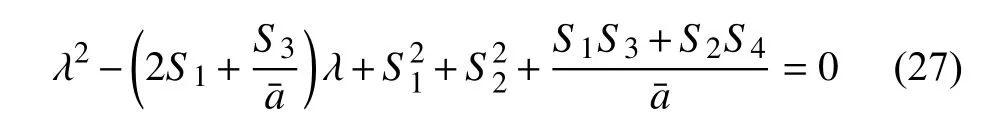
因此,系統定常解穩定的充要條件為

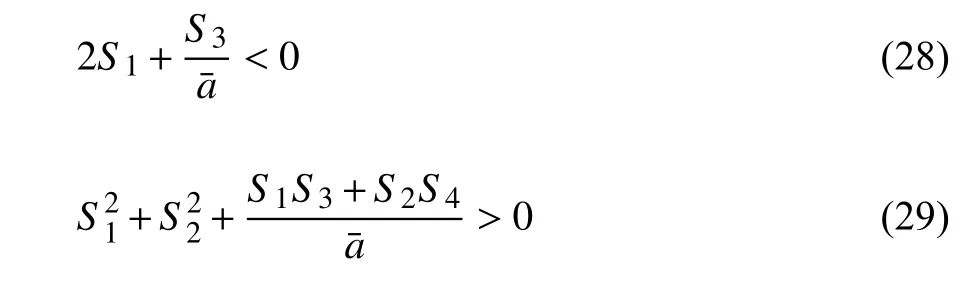
4 數值解驗證

根據參考文獻[13,38-39]選取一組示例參數值,具體參數為m=240 kg,c0=50 N·s/m,k=15 000 N/m,磁流變液阻尼器的參數選擇為:cf=300 N·s/m,fc=1000 N,分數階階次p=0.84,基礎激勵幅值為B=0.1 m.利用文獻[32]中的數值求解方法對系統進行數值計算,時間總長設定為188.5 s,以h=π/5000為步長,并將后62.8 s 響應的最大值作為穩態響應的峰值.通過計算發現,系統對于所有 τ≥0 始終滿足穩定性條件(29),說明當隔振器的作用與時滯反饋物理量無關時,時滯的引入未改變系統的穩定特性.

當系統處于被動控制(b=1)、不考慮時滯半主動控制(b=0.1,τ=0)、小時滯半主動控制(b=0.1,τ=40 h)、較大時滯半主動控制(b=0.1,τ=300 h)及(b=0.1,τ=580 h),以及大時滯半主動控制(b=0.1,τ=2000 h)時,根據數值解和近似解析解得到的幅頻響應曲線分別如圖3(a)～ 圖3(f)所示,圖中圓圈表示數值解,實線表示近似解析解.從圖3 中可以看出,系統在被動控制以及時滯較小的半主動控制時,近似解析解都與數值解具有很好的一致性,而時滯較大時,在共振峰值附近具有很好的一致性.系統在低頻(頻率小于 7rad/s)時數值解接近為0,是因為傳遞到磁流變液阻尼器的外力不足以克服其內部剪切摩擦力,使得系統幾乎沒有運動[14],此時半主動控制策略也不作用于系統.在半主動控制下,隨著時滯的增大,系統出現了明顯的高頻顫振,如圖3(d)～圖3(f)所示,而且時滯越大,高頻顫振問題愈加突出,振動控制效果惡化,因此,對于考慮時滯的天棚阻尼半主動控制系統而言,小時滯下的半主動控制才具有振動抑制的實際意義.

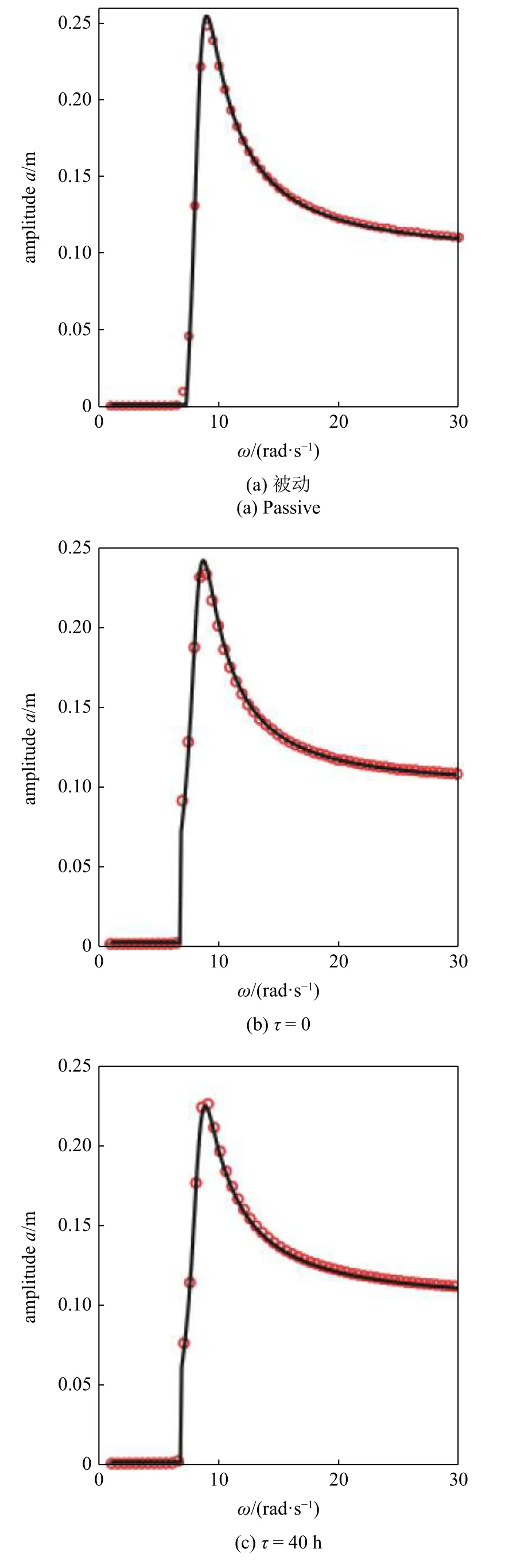
圖3 數值解與解析解的幅頻響應曲線比較Fig.3 Comparison of amplitude-frequency response for numerical solution and analytical solution

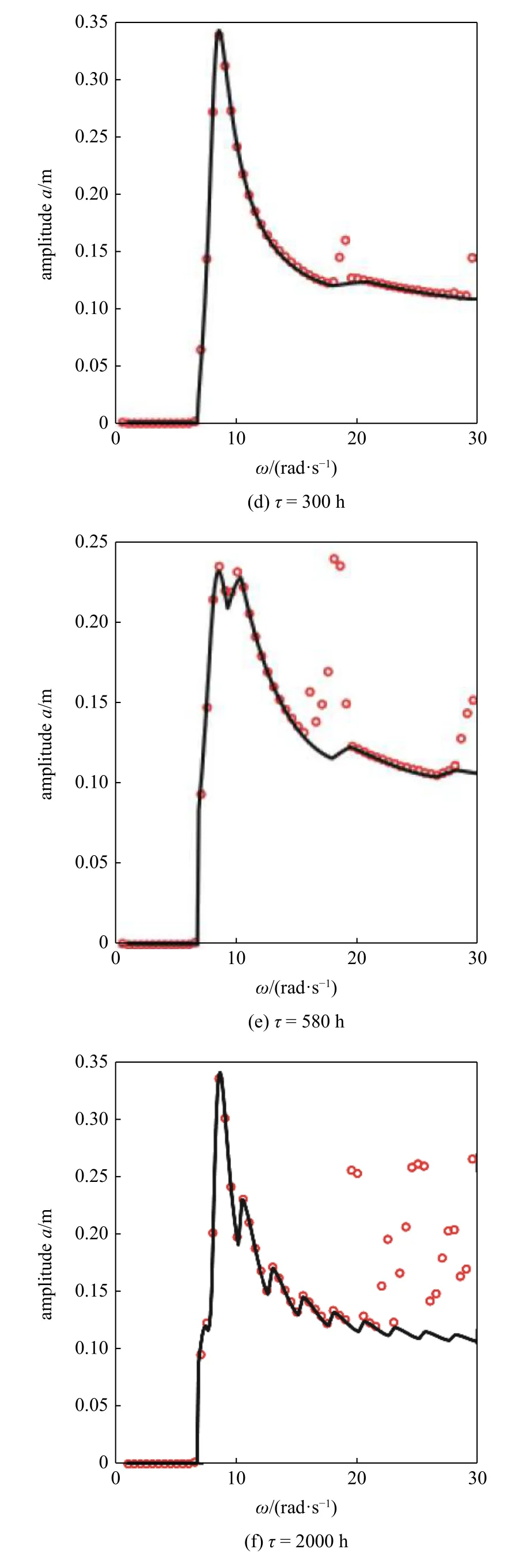
圖3 數值解與解析解的幅頻響應曲線比較(續)Fig.3 Comparison of amplitude-frequency response for numerical solution and analytical solution (continued)

5時滯對半主動控制的影響

為分析時滯對半主動控制(b=0.1) 的減振效果,對比圖3(a)～ 圖3(d) 4 種不同控制狀態和不同的小時滯控制參數時系統的幅頻響應曲線,如圖4 所示.可以看出,當時滯為0,40 h (25.1 ms)時在半主動阻尼控制下系統的穩態振幅在一定的激勵頻率范圍內優于被動控制(b=1)下的系統穩態振幅,可以有效地降低共振幅值.而當時滯為300 h (188.5 ms)時,反而會導致系統振幅的增大.相較于被動控制系統的幅頻響應曲線,不同時滯下的半主動阻尼控制不但會改變系統振動的峰值,其相應的共振頻率也會發生變化.

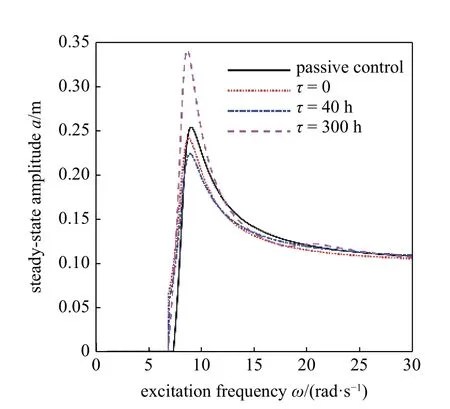
圖4 被動控制與不同時滯半主動控制的幅頻響應曲線對比Fig.4 Comparison of amplitude-frequency response curves between passive control and different time delay semi-active control

進一步研究時滯對系統振幅的影響規律.在天棚阻尼半主動控制策略下取時滯間隔為 5h,利用近似解析解獲得圖5 所示的激勵頻率為 ω=9 rad/s 和ω=10 rad/s 時系統穩態幅值-時滯響應曲線.在固定激勵頻率下系統的振幅呈現出與頻率相關的固定周期的變化規律,頻率越大所對應的變化周期越小.

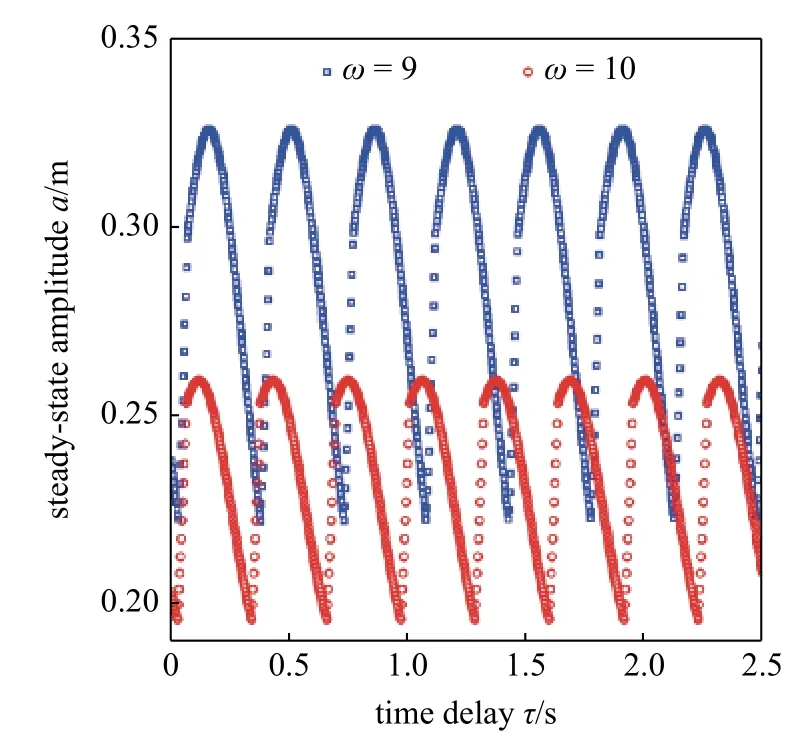
圖5 固定激勵頻率下系統穩態幅值-時滯響應曲線Fig.5 Steady-state amplitude with time delay under the fixed excitation frequency

根據近似解析解得到系統主共振峰值-時滯響應曲線如圖6 所示.從圖中可以看出,主共振峰值amax隨時滯 τ的變化是非簡諧的,但amax出現了明顯的周期性變化規律,而且隨著時滯 τ 的增大,主共振峰值所能達到的最小值越大.對比被動控制下主共振峰值(約為0.255 m),當時滯為364.4 ms (τ=580 h)時系統的主共振峰值也小于被動控制下的主共振峰值.但是由圖3(e)可知,由于時滯的增大系統會出現高頻顫振,因此只考慮第一個時滯周期內的時滯量作為時滯參數.由圖6 得到,當系統的固有時滯小于44 ms (τ=70h)時,在此范圍內的時滯半主動控制均可以達到優于被動控制的目的;當系統的固有時滯大于44 ms 時,半主動控制在時滯的影響下,會導致系統的振動抑制效果惡化,此時被動控制效果則優于半主動控制.特別地,在時滯為28.3 ms (τ=45h)時,時滯天棚阻尼控制策略可以達到最優減振效果,即當系統的固有時滯小于此最優時滯時,可以對控制系統引入時滯使其達到此最優時滯,使得系統主共振峰值最低.

圖6 主共振峰值隨時滯的變化曲線Fig.6 Primary resonance peak with time delay

改變半主動控制參數b為0.3 和0.6,繪制主共振峰值隨時滯的變化曲線如圖7 所示.可以看出,隨著半主動控制參數b的減小,時滯變化時主共振峰值的變化增大,但是對最優時滯區間沒有影響.在最優時滯區間內,半主動控制參數b越小,主共振振幅越小.

圖7 不同參數 b時系統主共振峰值隨時滯的變化曲線Fig.7 Primary resonance peak with time delay of differentb

主共振峰對應的共振頻率-時滯響應曲線如圖8 所示,其對應的共振頻率 ωr隨時滯 τ 的變化也是非簡諧的,半主動控制參數b越小,主共振峰對應的共振頻率變化范圍越大.

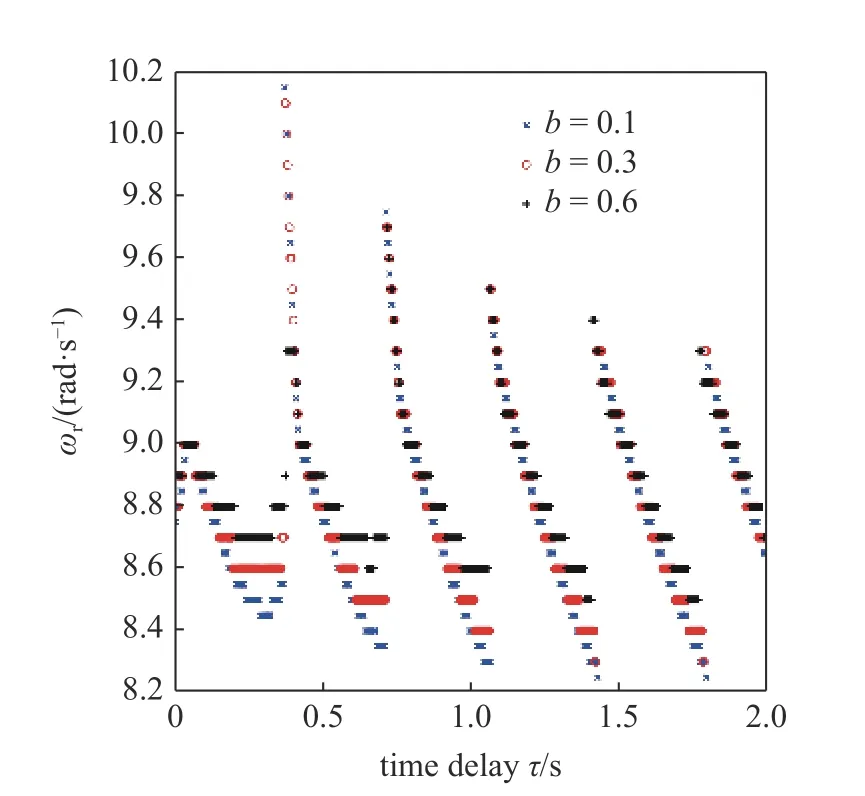
圖8 不同參數 b時共振峰值對應的頻率-時滯曲線Fig.8 Frequency corresponding to resonance peak with time delay of differentb

6 結論

本文對基于磁流變液阻尼器的隔振系統在含有時滯的半主動控制策略下的系統共振響應及其振動特性進行了分析.針對含有磁流變液阻尼器的半主動阻尼控制系統中存在的時滯問題,將時滯引入半主動控制切換條件中,利用平均法對基于分數階Bingham 模型的線性剛度系統在天棚阻尼控制下的主共振響應進行了解析研究,得出系統的近似解析解,并通過數值計算驗證了解析結果的準確性,解析結果與數值解具有較好的一致性.采用Lyapunov 方法分析了系統的穩定特性,而且在全頻域內,時滯的引入并不會改變原系統的穩定性.通過分析時滯對系統幅頻響應曲線的影響,表明在一定的小時滯范圍內,與被動控制相比,時滯半主動控制策略可以有效地降低主共振峰值,達到系統減振的目的.并且存在一個時滯量的取值區間,使系統的振幅在一定的激勵頻率范圍內低于被動控制系統,且在這個區間上會存在一個時滯點,使得系統的振幅得到最大幅度的降低.當系統固有時滯小于最優時滯時,在半主動阻尼振動控制系統的實際應用中即使不考慮時滯,也會使系統在一定的激勵頻率范圍內得到滿意的振動控制效果.然而大時滯的引入會導致系統的顫振,使系統的減振效果變差.本文的分析為實際工程應用中的半主動阻尼振動控制系統時滯選取提供了依據.