軟體連續機械臂動力學建模與仿真1)

白爭鋒 孔清峰 趙 起

(哈爾濱工業大學(威海)機械工程系,山東威海 264209)

引言

軟體機器人以其無限自由度、被動變形適應環境和柔順接觸等優勢在醫學、航天、農業、汽車、制造、核能、醫療保健和康復、環境保護和海洋勘探、反恐偵察等方面有著廣闊的應用前景[1-3].在過去十多年中,軟體機器人成為眾多學者研究的對象.仿象鼻、章魚觸手等結構的機械臂式連續體機器人,以其固有的柔順性,安全性及適應非結構化環境的優良特性使其顯示出巨大的應用潛力,成為目前機器人領域的熱門研究方向之一[4-8].

目前,研究人員針對軟體機械臂進行了一系列的研究,并取得了一些研究成果.Walker 等[9-13]對軟體機械臂建模做了大量研究,Renda 等[14]設計的仿章魚軟體機械臂樣機,基于Cosserat 梁理論將軟體機械臂軸線表示為空間中的一維曲線,并考慮了纜索驅動機器人的相關彈性力、驅動力和重力,建立了肌腱驅動的軟體機械臂運動學及靜力學模型;基于Kelvin-Voight 線性黏彈性本構方程建立Cosserat 應變模型[15],建立軟體章魚臂機器人在水下環境中的動力學模型;其后提出一種基于離散化Cosserat 理論的分段恒應變[16]方法,并建立了軟體機械臂的運動學和動力學模型.然而該方法推導出的動力學方程是一組耦合偏微分方程,在數值求解上十分困難.Kang 等[17-19]利用章魚生理解剖結構,基于分布式的彈簧-阻尼模型模擬章魚臂4 個縱向和4 個徑向肌肉,建立了章魚機械臂的三維動力學模型,但是該模型沒有從能量的角度考慮集中質量模型,并且使用歐拉遞推法建立動力學方程,方程推導十分繁瑣.Rone 和Ben-tzvi[20]使用一組有限的運動學變量來捕獲機械臂的曲率變化,基于虛功原理為肌腱驅動的軟體機械臂建立了動力學方程;在推導動力學方程中考慮了慣性、致動、摩擦、彈性和重力等效應.然而該方法推導連續臂的動力學方程會導致復雜的非線性積分,除了固有的數值不穩定性之外,這些積分在計算上是不可行的,因此該方法有一定的局限性.

Tatlicioglu 等[21]基于恒定曲率和分布式質量建立了可變長度連續體機械手平面動力學模型,并考慮了重力勢能項和彈性勢能項,使模型與機械臂的真實行為相一致.Falkenhahn 等[22-23]提出了一類稱為仿生操作助手的連續機械手的動力學模型,該模型采用歐拉-拉格朗日方法,并基于分段常曲率假設,將每個段的質量看作集中質量放置在每段的末端位置.該模型雖然在數值計算上可行,但是將每段質量看作位于頭部的集中質量并不能從能量上與實際的分布式質量相匹配.Giri 和Walker[24]建立了三段式平面軟體機械臂動力學模型,然而該模型將每段的質量看作位于末端的集中質量.針對軟體機器人變形后呈圓弧形狀彎曲,Mazzolaii 等[25]提出分段常曲率(PCC)理論模型.對于變曲率彎曲問題,可將軟體機器人本體結構分為多段,假設每段曲率恒定,每段形狀可通過曲率半徑、兩截面所在平面間夾角以及兩截面扭轉角來描述[26-27],然后建立末端截面與坐標系的關系.

軟體機械臂動力學模型數值求解精度與計算效率對于軟體機械臂的動態控制至關重要.本文基于模態方法推導軟體機械臂運動方程,明確地從能量的角度考慮軟體機械臂動力學特性,提出一種基于質心集中質量的軟體機械臂動力學模型,該模型將軟體機械臂的分布質量等效為位于質心的集中質量,通過動能等效系數實現二者的動能匹配.與將集中質量放置在任意位置(例如,軟體機械臂的末端)的集中質量模型相比,該模型兼顧了采用連續分布質量進行拉格朗日方法分析時的準確性,以及采用離散化的集中質量模型分析時的計算高效性.仿真結果表明,本文提出的將集中質量放置在與機械臂的能量行為相匹配的位置所建立的軟體機械臂集中質量動力學模型,能夠準確、高效地捕獲軟體機械臂的動力學特性,并且數值計算穩定.

1 運動學建模

1.1 軟體機械臂模型抽象

將軟體機械臂抽象為如圖1 所示的結構,軟體機械臂由三個結構完全相同的驅動器組成,且均布在間距為120°以r為半徑的輕質圓形剛性框架上,剛性框架實現了三個驅動器在空間上隔離與固定.結構中也等間隔分布圓形剛性框架,以保持驅動器軸線方向始終平行于中性軸,假設剛性框架相對于驅動器的質量可以忽略不計.三個驅動器的初始長度均為 ?,各驅動器的總長度隨時間變化規律為?+?k(t),k∈{1,2,3},k表示軟體機械臂上三個驅動器的編號,其中 ?k(t) 表示各驅動器長度的變化量,并且驅動器長度的變化量在一定的范圍內,即 ?min,?max均為定值,其物理意義是驅動器的最大壓縮量或最大伸長量.如圖1(a)描述的是軟體機械臂在空間中彎曲后的形狀,軟體機械臂在空間中彎曲成一段圓弧,C點表示圓弧的曲率中心,全局參考系 {R} 的原點O與軟體機械臂下底面的中心重合,將驅動器1 的底端落在X軸正方向上的A點,驅動器2 和3 按逆時針方向布置,分別對應于B點和D點.

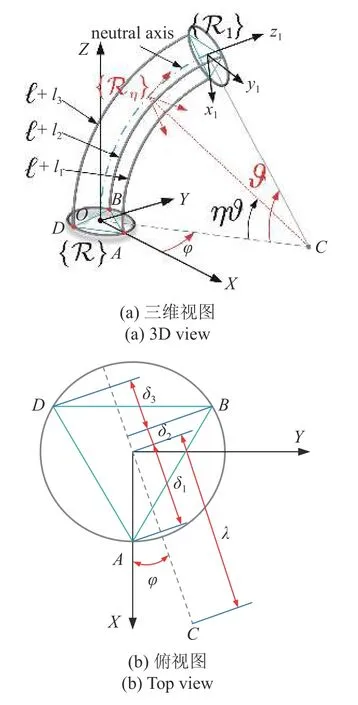
圖1 空間軟體機械臂示意圖Fig.1 Schematic diagram of space soft manipulator

為了簡化分析,在軟體機械臂運動學建模時提出以下基本假設:

(1) 軟體機械臂變形過程中,各驅動器假定為彎曲曲率相等的光滑連續曲線;

(2) 驅動器變形過程中不考慮扭轉變形;

(3) 驅動器僅沿長度方向變化,徑向尺寸不發生改變;

(4) 軟體機械臂沿長度方向具有均勻面密度.

1.2 驅動空間到配置空間的映射

為描述軟體機械臂的運動,引入如下坐標系:全局參考系 {R}固連在機械臂的底端,局部參考系{R1}固連在上端,并且z1軸與中性軸相切.根據假設(1),軟體機械臂變形后在空間中的配置可以由一組曲線參數完全定義,曲率半徑λ ∈(0,+∞),瞬時曲率中心C;彎曲張角?,以及彎曲平面相對于X軸正方向的轉角 φ∈[-π,π] .為了獲得末端執行器的位姿與驅動器的長度變化量的關系,定義三個空間與兩個映射.如圖2 所示,三個空間分別為:代表驅動空間關節變量;代表配置空間關節變量;H代表局部參考系 {R1}到全局參考系{R}的齊次變換矩陣,x代表任務空間,即軟體機械臂末端的笛卡爾空間.兩個映射分別為:fspecific表示從驅動空間到配置空間的映射,即 κ=κ(q),fgeneral表示從配置空間到任務空間的映射,即H=H(κ) .根據文獻[28]可以建立驅動空間到配置空間的映射關系為

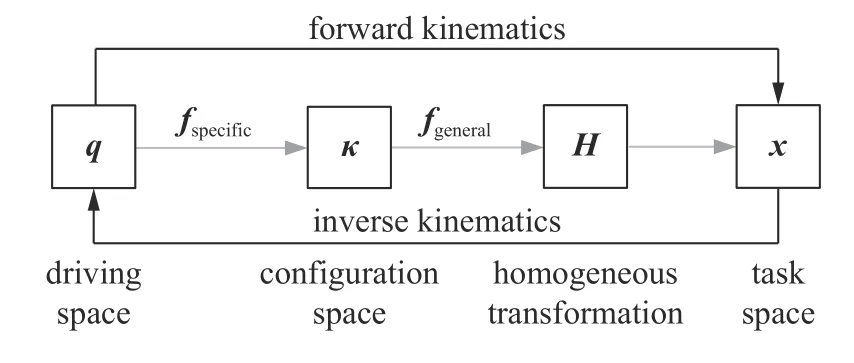
圖2 不同空間的運動學映射Fig.2 Kinematic mapping of different spaces

1.3 配置空間到任務空間的映射

考慮配置空間κ到任務空間x的映射關系,即求解局部參考系{R1}到全局參考系 {R} 的齊次變換矩陣H.齊次變換矩陣需要經過如圖3 所示的5 個步驟得到,分別為:首先,繞全局坐標系 {R} 的Z軸旋轉角度φ;然后沿著當前參考系X軸正向移動距離λ;接著繞當前參考系的Y軸旋轉角度?;再沿著當前參考系的X軸負方向移動距離λ;最后繞著當前參考系Z軸旋轉角度-φ,最終得到配置空間到任務空間的齊次變換矩陣為

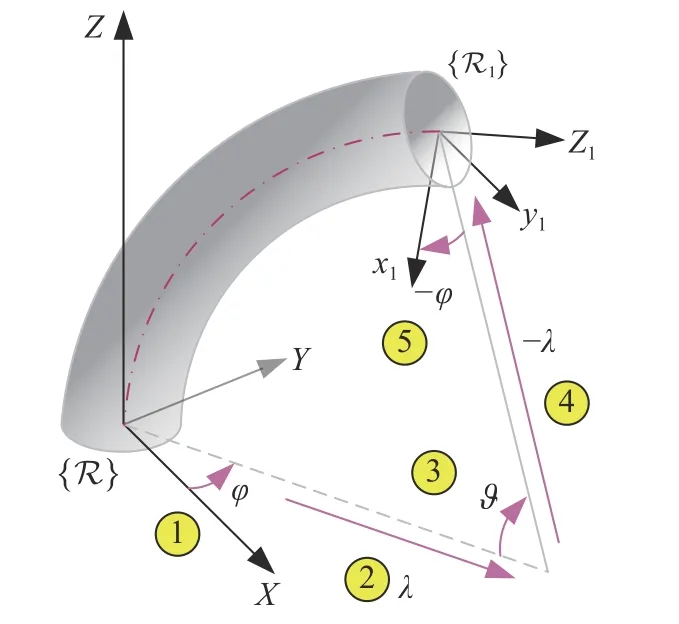
圖3 齊次變換矩陣的生成步驟Fig.3 Steps of homogeneous transformation matrix

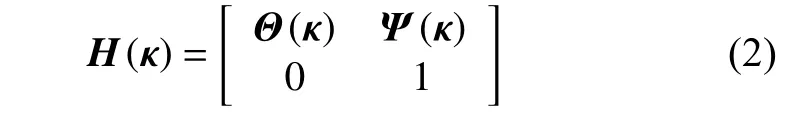
式中,Θ(κ)∈R3×3表示局部參考系 {R1} 到全局參考系{R}的旋轉矩陣,ψ(κ)∈R3×1表示局部參考系{R1} 到全局參考系 {R} 的位置平移向量.

Ψ(κ,η)∈R3×1表示動參考系到全局參考系的位置平移向量,該向量中的3 個元素表達式如下

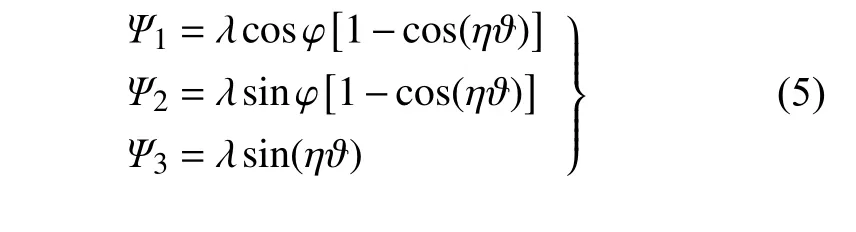
1.4 配置參數的局限性

式(3)給出的齊次變換矩陣包含關節空間中連續體中性軸上任意點的位置和方向,但該矩陣中的每個元素都是由三角函數構成.由于三角函數屬于復雜的非線性函數,并且該式中使用的配置參數為λ和φ,這兩項中的分母分別為和l2+l3-2l1,這將產生一個不可避免的問題,即當l1=l2=l3時,這兩項的分母都將變為零,隨之導致數值計算的奇異性與不穩定性.如果采取一種處理方式,將齊次變換矩陣中各元素近似為數值穩定的多元多項式,則可避免奇異性問題.不同類型的級數展開法,如冪級數、傅里葉級數以及泰勒級數均可用于簡化復雜的非線性函數[29].考慮到軟體機械臂連續變形的特性,多元泰勒級數展開不含三角項的多項式與具有驅動空間關節變量的分母,因此能夠有效消除數值計算的奇異性與不穩定性.

本文在描述軟體機械臂變形后的空間位置描時,使用模態方法代替配置參數導出的運動學方程,從而避免奇異性.模態方法是利用簡單的多項式函數逼近復雜的非線性函數,同時,利用模態坐標將會極大提高動力學方程求解效率.鑒于此,將式(3)展開為三元泰勒級數,齊次變換矩陣H用模態齊次變換矩陣T近似表達,本文給出截斷誤差具有11 階精度的模態變換矩陣的表達式,為表示方便,令

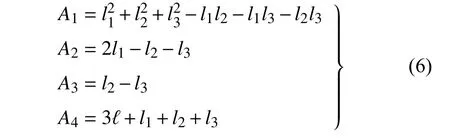
則模態變換矩陣T中模態旋轉矩陣R的表達式如下

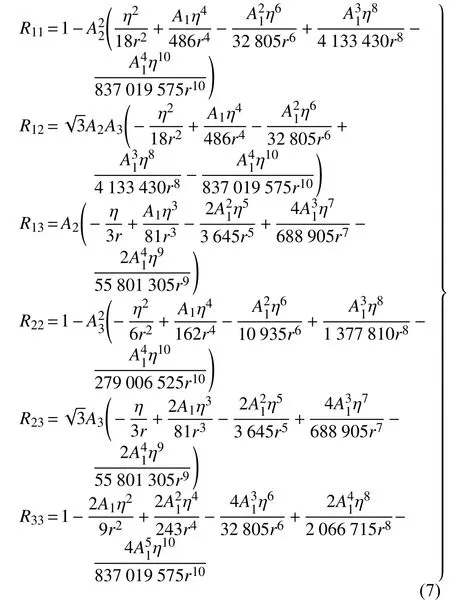
模態變換矩陣T中模態位置平移向量p的表達式如下

則軟體連續臂中性軸上任意點到全局參考系的模態齊次變換矩陣為

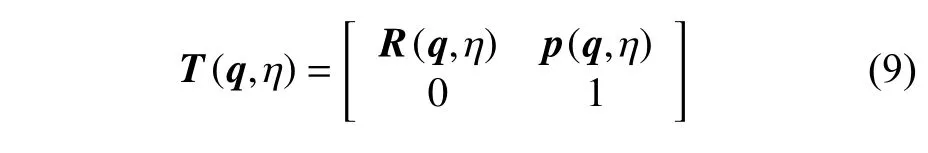
基于泰勒級數的模態方法提供了一個直觀和直接的選擇,使齊次變換矩陣H中的每個元素產生唯一且精確的多項式函數,因此,它避免了模型轉換和模型奇異性.此外,軟體機器人正運動學和逆運動學都可以在空間關節中直接計算,而不需要額外的奇異性解決方法,并且所提出的方法可以簡便地擴展到多節連續機械臂的動力學建模中.

2 連續機械臂動力學建模

通常認為機械臂的質量是沿臂的長度均勻連續分布的,如圖4(a)所示.本節首先考慮機械臂的質量是沿臂的長度均勻連續分布的,基于拉格朗日方法建立軟體機械臂動力學模型;然后提出基于質心集中質量的動力學模型,機械臂的質量位于質心處,如圖4(b)所示.

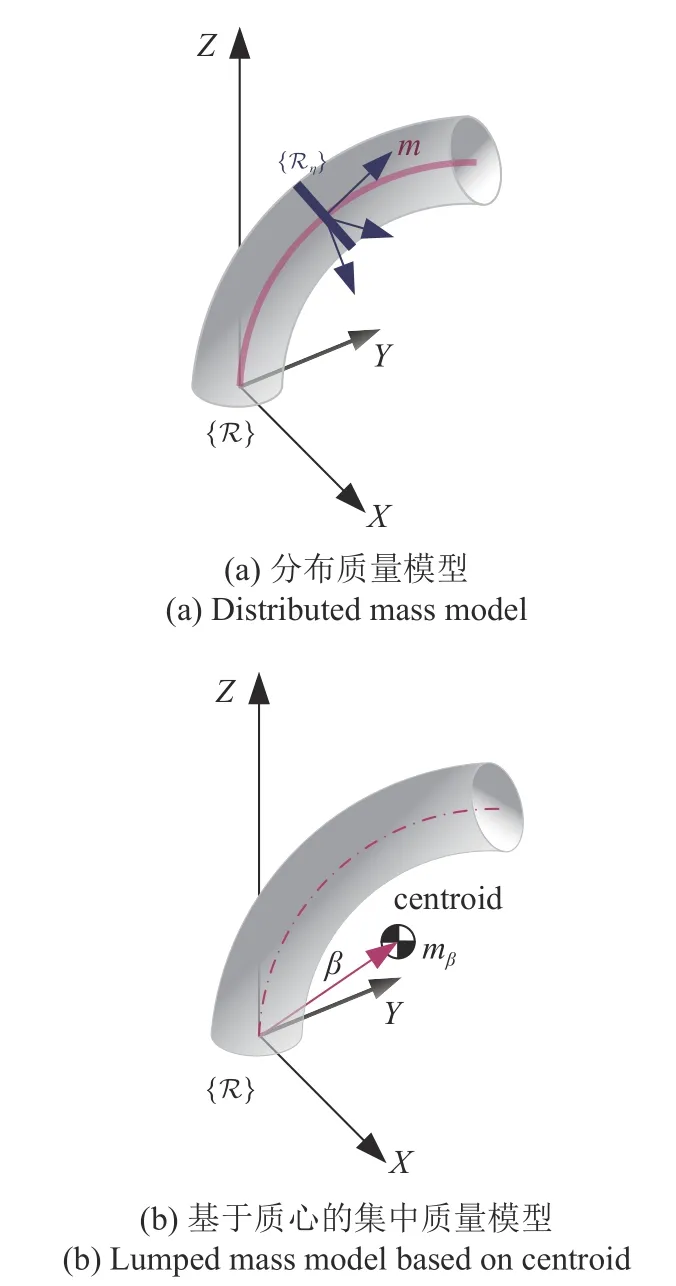
圖4 兩種動力學模型Fig.4 Two kinds of dynamics model

2.1 分布質量動力學建模

軟體機械臂的拉格朗日函數可以寫為 L=K-P,其中 K 表示軟體機械臂的總動能,P 表示軟體機械臂的總勢能.總動能 K=Kυ+Kω,Kυ表示軟體機械臂的平動動能,Kω表示軟體機械臂的轉動動能.總勢能 P=Pg+Pe,Pg表示軟體機械臂的重力勢能,Pe表示軟體機械臂的彈性勢能.為獲得以上各能量項的表達式,如圖5 所示基于微分的思想將軟體機械臂沿中性軸看作無窮多個切片組成,中性軸上η處切片的示意圖如圖6 所示,將切片看作質量為mdη,厚度為λ?dη,半徑為r的均質圓盤.位于η處切片的動能與勢能得到后,通過從底部到頂部對η從0 到1 積分確定軟體機械臂的總能量.

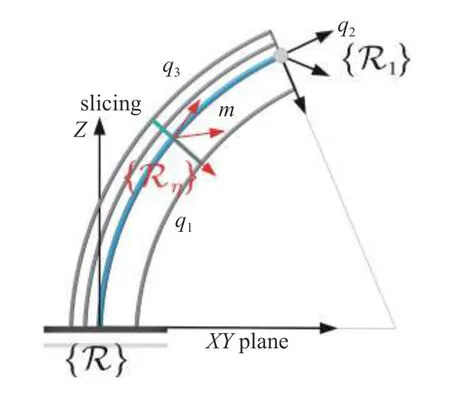
圖5 切片示意圖Fig.5 Schematic of slice

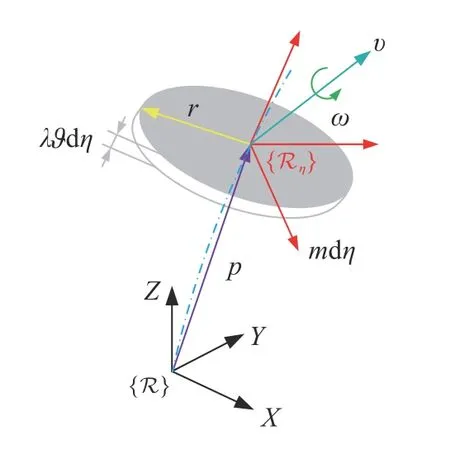
圖6 切片放大示意圖Fig.6 Slice enlargement

2.1.1 動能計算

為確定軟體機械臂的總動能,采用式(9)推導的模態變換矩陣獲得切片的瞬時速度,包括線速度ν與角速度ω.將式(8)對時間求導可得中性軸上任意點η處切片相對于全局參考系 {R} 的線速度為

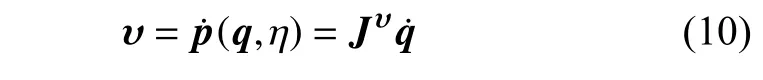
式中,線速度雅可比矩陣Jn表達式為

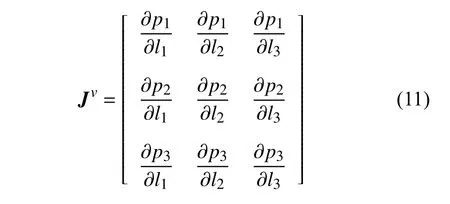
中性軸上點η處切片在體參考系 {R1} 中的角速度為

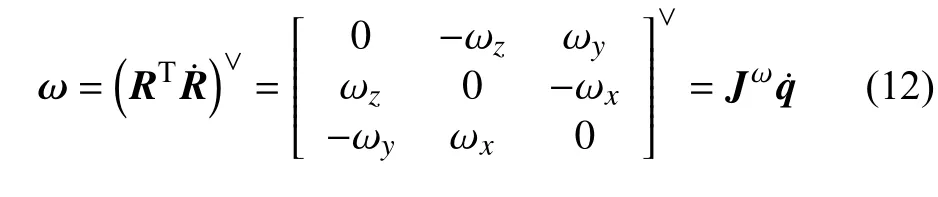
式中,操作符 ∨ 表示對反對稱矩陣提取非零元素,且角速度的三個分量為

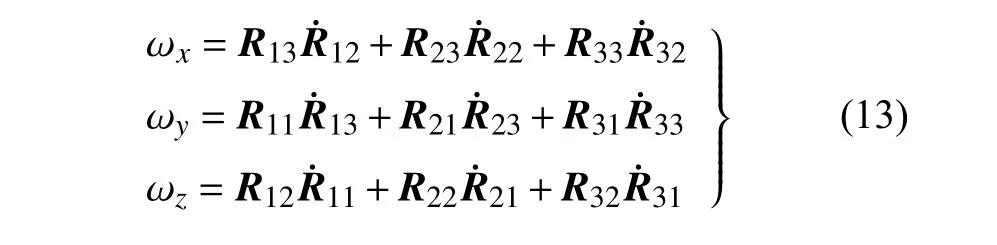
由于假定軟體機械臂的質量恒定且具有均勻的面密度,因此切片質量mdη具有的線慣性矩陣為Mυ=mdηI3,I3為三階單位矩陣.又由于假定切片具有圓形截面,因此其具有的慣性張量為Mω=Ixxdiag(1,1,2),其中表示對角矩陣.將質量相關的切片能量對 η 進行積分,則軟體機械臂的平動動能為

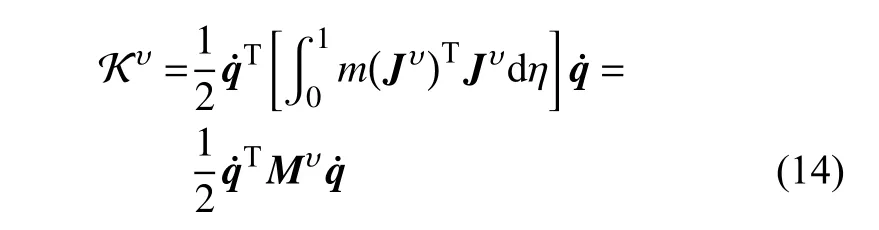
同理,軟體機械臂的轉動動能為

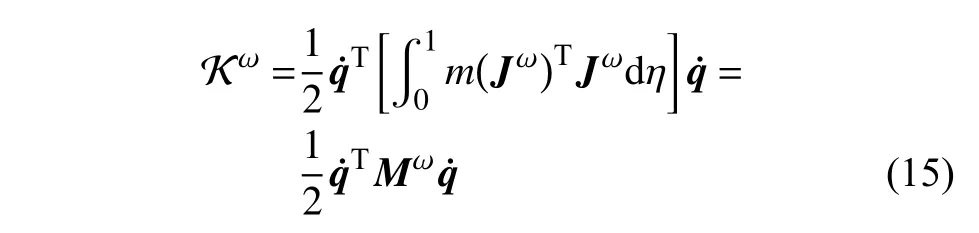
則軟體機械臂總動能為

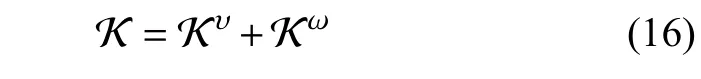
2.1.2 勢能計算

軟體機械臂的勢能主要包括兩部分,分別為重力勢能和彈性勢能,依次進行計算.中性軸上任意點η處切片具有的質量為mdη,則其重力勢能為

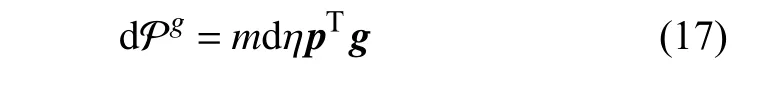
故整個軟體機械臂的重力勢能為

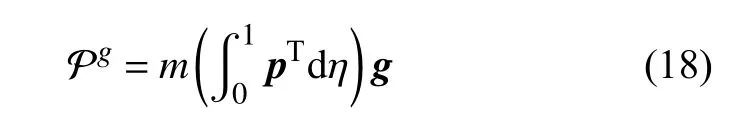
式中,g=[0,0,g]T,g表示重力加速度常數.

彈性勢能是由于三個驅動器的伸縮效應引起的.驅動器的彈性勢能需要根據驅動器所使用的不同的材料建立不同的函數關系[30].一般而言,彈性勢能是變形量的函數,即 Pe=f(q) .本文忽略驅動器材料的剪切變形,假設驅動器材料是線彈性的,即驅動器的彈性勢能正比于伸長量的平方.因此,軟體機械臂的剛度矩陣可以寫為

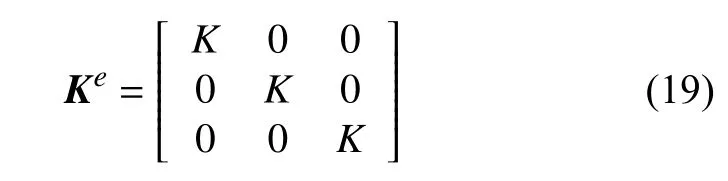
從而軟體機械臂的彈性勢能為

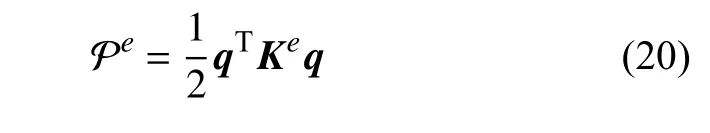
獲得以上各能量項后,則軟體機械臂的拉格朗日方程為

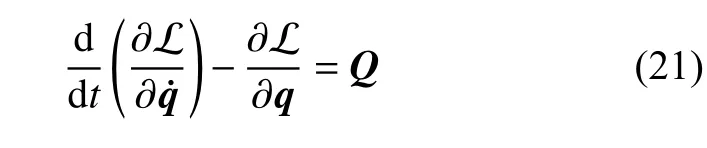
進而,該軟體機械臂驅動關節空間中的拉格朗日動力學方程以矩陣形式表示為

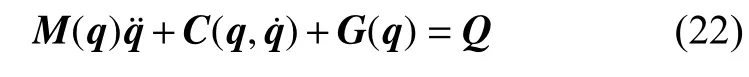
式中,M∈R3×3為機器人的質量矩陣;C∈R3×3為離心力與科里奧利矩陣;G∈R3×3為保守力矢量;Q∈R3×3為外力矢量.

質量矩陣為

保守力矩陣為

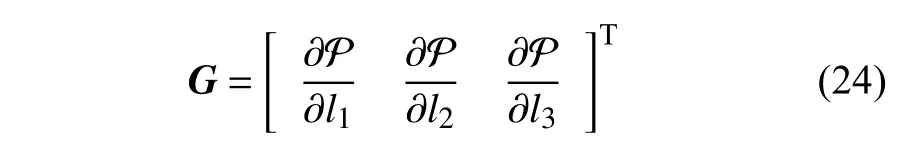
2.2 能量分析與方程簡化

由于軟體機械臂的軸向尺寸遠大于其徑向尺寸,本節對軟體機械臂的平動動能和轉動動能進行定量評估.平動動能與轉動動能是驅動空間變量q和驅動空間速度的函數,但驅動空間變量受驅動力的影響,隨時間變化的規律多樣,導致是變化多樣的,盡管q與變化規律不定,但受到材料物理極限的限制,兩者的變化量必位于某一范圍內.假定軟體機械臂驅動器的長度變化范圍為 [0,30 mm],并且其速度變化范圍為 [-50,50 mm/s],在此條件下,通過使用全局搜索計算得到 0≤Kω/K ≤3% .

進而,采用一具體的數值算例對動能進行分析,以便直觀的揭示轉動動能 Kω占總動能 K 的比值.假定軟體機械臂的三個驅動器長度變化量隨時間變化規律為,0≤t≤2π,根據驅動器的變化規律,首先計算軟體機械臂末端的線速度與角速度,分別如圖7 和圖8 所示.

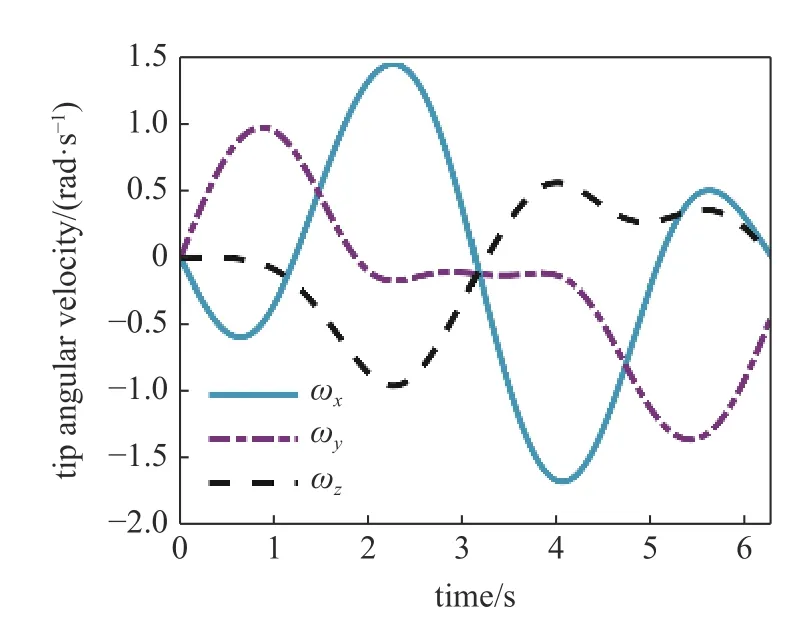
圖8 角速度變化曲線Fig.8 Angular velocity

由圖7 可以看出線速度的大小為每秒幾十毫米,角速度的大小為1 rad/s 左右,這顯然符合正常的速度值范圍,因此無法通過線速度與角速度的大小關系來判斷平動動能和轉動動能的大小關系.值得注意的是,在推導二者表達式時得到軟體機械臂的平移質量矩陣為 Mυ=mI3,轉動質量矩陣為Mω=,兩者的數量級是不同的,進而可以定性的判定出平動動能要遠大于轉動動能.

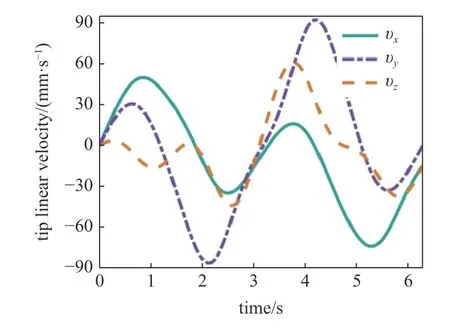
圖7 線速度變化曲線Fig.7 Linear speed

進一步經定量計算得到二者隨時間的變化規律如圖9 所示,為 Kω和 Kυ隨時間變化曲線,從圖9 中可以直觀地看出轉動動能遠小于平動動能.如圖10所示為 Kω占總動能 K 的比值隨時間的變化圖,可以發現兩者比值最大值不足 1.2%,由此可見,轉動動能Kω占總動能 K 的比值很小.另外,根據式(11)和式(12)可以看出,角速度雅可比Jω的計算量要比線速度雅可比Jυ的計算復雜的多,然而其對整個動能的占比又非常小,因此為了簡化計算,在建模過程中轉動動能可以忽略不計.本文下述動力學分析過程中,均不考慮轉動動能,即 K≈Kυ.

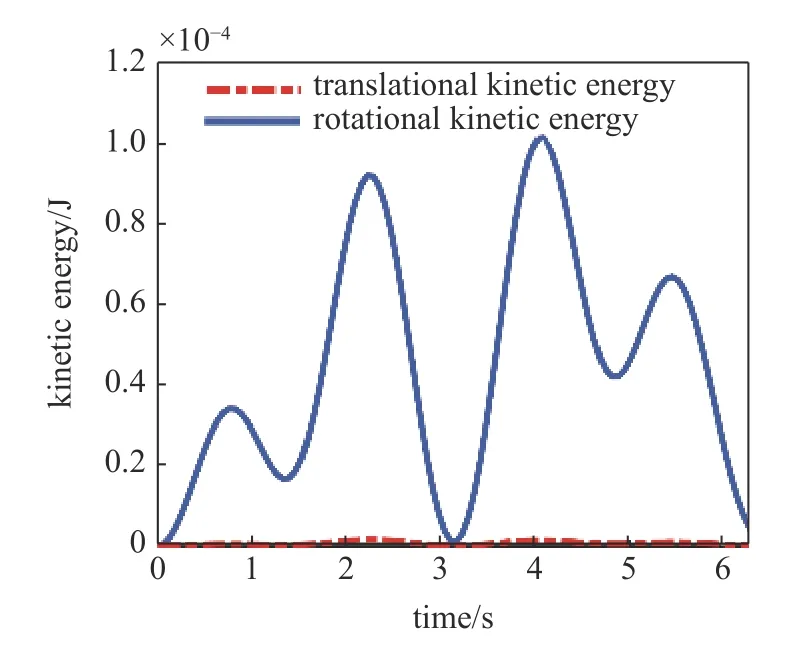
圖9 動能變化曲線Fig.9 Kinetic energy

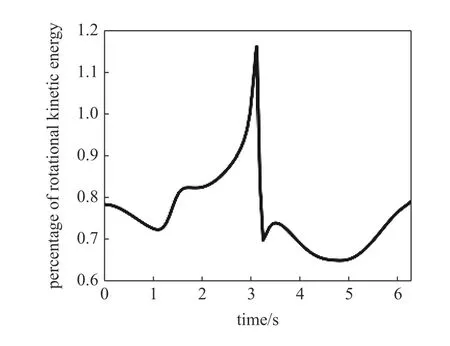
圖10 轉動動能占總動能百分比Fig.10 Percentage of rotational kinetic energy

如圖11 所示為軟體機械臂的彈性勢能以及重力勢能隨時間的變化規律.初始時,軟體機械臂處于未致動狀態,此時三個驅動器的長度均未發生變化,因此彈性勢能為零.但重力勢能恰好為mg?/2=0.112 5 J,隨著驅動器長度的變化,重力勢能的變化范圍并未出現較大的波動,這是因為軟體機械臂的質心位置在Z 軸方向上的位移沒有發生太大變化,該現象從圖12 也能明顯發現.彈性勢能的變化范圍較大,這主要是驅動器長度變化范圍引起的.需要特別指出的是,彈性勢能與重力勢能的大小在同一數量級上,這一點不同于平動動能和轉動動能,因此,二者均需要在動力學方程中考慮.

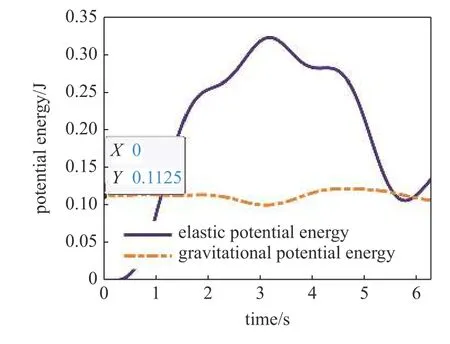
圖11 勢能比較Fig.11 Potential energy comparison

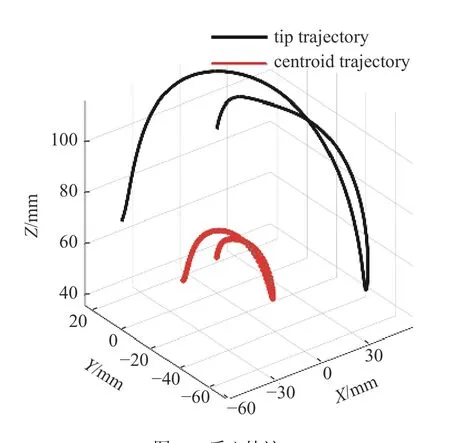
圖12 質心軌跡Fig.12 Trajectory of mass center

通過以上對軟體機械臂能量進行計算分析得出如下結論:第一,平動動能遠遠大于轉動動能,因此在動力學方程中忽略轉動動能;第二,重力勢能與彈性勢能處于同一數量級,二者均要在動力學方程中考慮.

2.3 基于質心集中質量動力學建模

考慮基于質心集中質量的動力學模型,質心在動力學分析中具有重要的地位,特別是在剛體力學中,其地位顯得尤為重要.事實上在處理大變形問題時,也可以基于質心進行分析,在軟體機械臂建模方面,已經提出了許多集中參數模型.然而,近似軟體機械臂的平滑彎曲需要將其劃分成很多小段或集中質量點,這顯著增加了模型的自由度和計算的復雜性[31],迄今為止,集中質量建模研究的重點主要是降低計算復雜性,而沒有充分考慮各種近似值在能量域中是否具有良好的匹配精度.本小節將從能量的角度考慮軟體機器臂動力學,將集中質量放置在與機械臂的能量行為相匹配的位置(即質心位置).與將集中質量放置在任意位置(例如每個部分的尖端)的集中質量模型相比,基于質心集中質量的動力學模型更接近基于分布質量建立的動力學模型,且沒有積分項,計算效率高,并且數值穩定.

2.3.1 基于質心的集中質量動力學建模

基于質心集中質量模型對軟體機械臂進行動力學分析,隨著驅動器長度的變化,軟體機械臂在運動時,其構型時刻發生改變,導致其質心位置不斷發生改變,并且軟體機械臂在運動過程中,其質心位置不一定位于幾何體上.圖12 顯示了隨著機械臂的構型發生變化,其質心的位置也在不斷改變.

盡管質心的位置在不斷變化,但可以確定的是,軟體機械臂質心位置矢量 β∈R3×3必然是驅動空間q的函數,且具有如下表達式

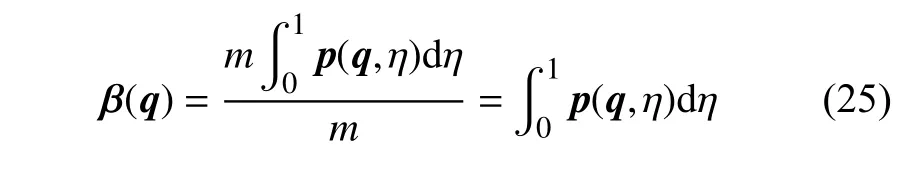
上式對時間求導可得質心的速度為

式中,Jβ表示速度雅可比矩陣且具有如下表達式

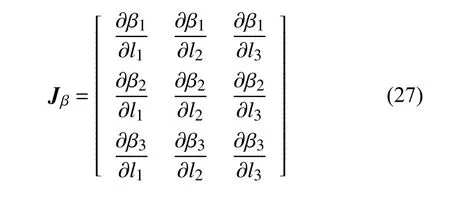
因此基于質心的動能為

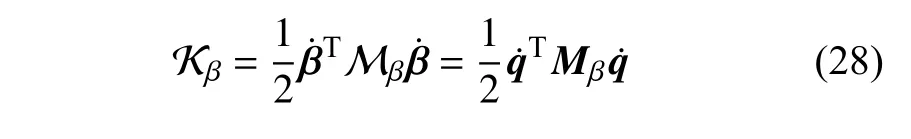
同理,基于質心的重力勢能為

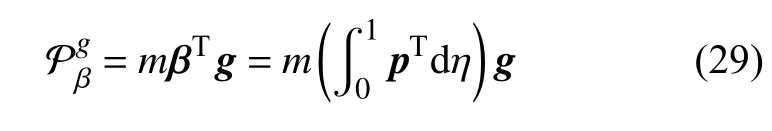
對比式(18)與式(29),不難發現基于質心集中質量模型所求軟體機械臂的重力勢能和采用連續分布質量所求的動力學模型相等.進一步分析基于質心所求的軟體機械臂的動能 Kβ與采用連續分布質量積分所求的動能 K,顯然,兩種方式計算出的動能都是驅動空間變量q以及其導數的函數,但驅動空間受驅動力的影響,其隨時間變化的規律是不確定的,將影響的變化,盡管其變化規律不定,但受到物理極限的限制,兩者的變化必定位于某一范圍內.為了比較 Kβ與 K 的數量關系,現假定兩者的變化范圍為[0,30 mm],[-50,50 mm/s],在該范圍內隨機生成10 000 個數據點來比較兩者的數量關系,結果如圖13 所示.

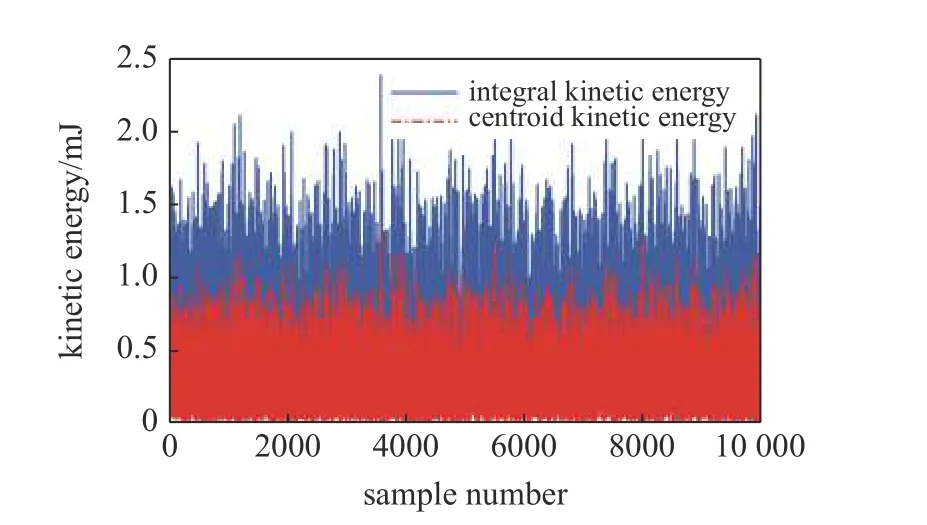
圖13 隨機樣本下動能大小Fig.13 Kinetic energy under a random sample

顯然兩者的大小并不相等.進一步研究兩者的比值關系,即對每一個隨機數據點計算,計算結果如圖14 所示,由圖發現比值的范圍落在區間 [0.5,0.75] 內,并且大致以0.56 為中心上下波動.將區間 [0.5,0.75] 以0.05 為間隔劃分為五個子區間,對隨機生成的10 000 個數據點落在各區間的數量進行統計,統計結果見表1.

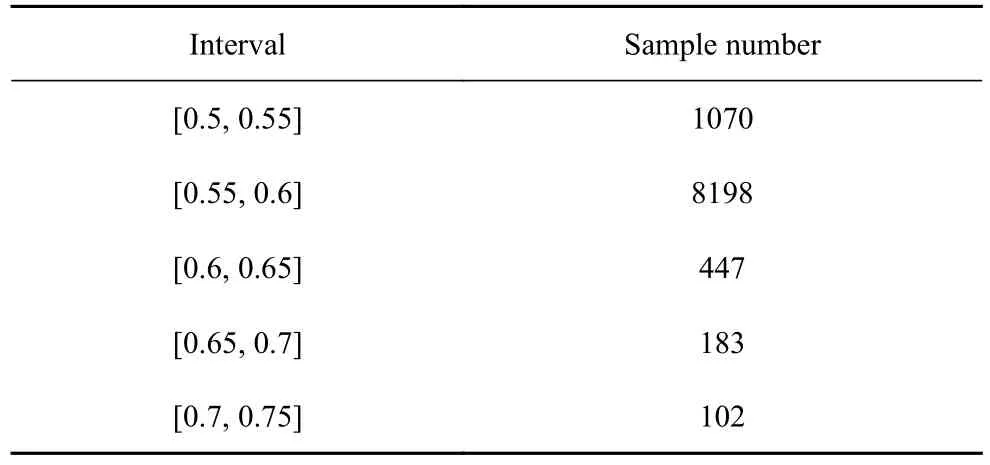
表1 樣本點落入各區間的個數Table 1 The number of sample points falling into each interval

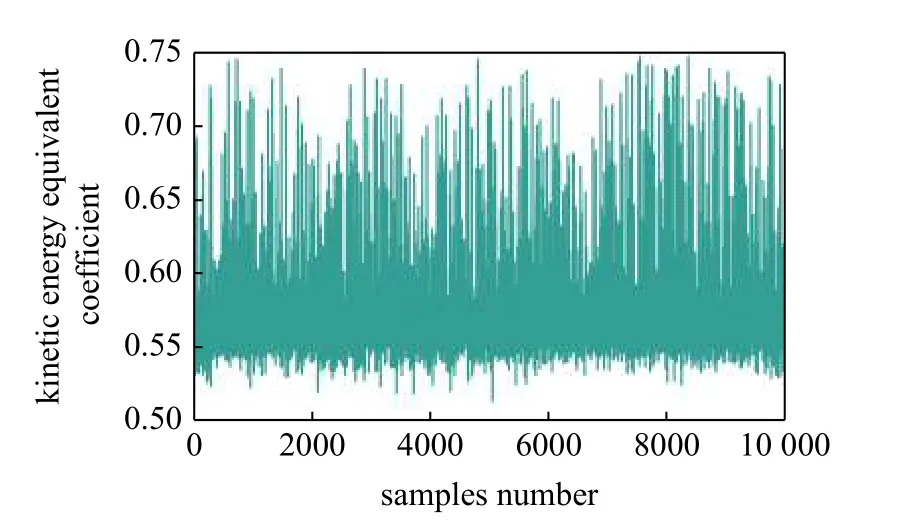
圖14 動能等效系數Fig.14 Kinetic energy equivalent coefficient

計算落在每個子區間的概率,繪制成如圖15 所示的條形圖,由圖15 可知,落在0.5 到0.6 之間的概率約為 93% ,均值記為 ξ,計算結果為 ξ=0.56 .

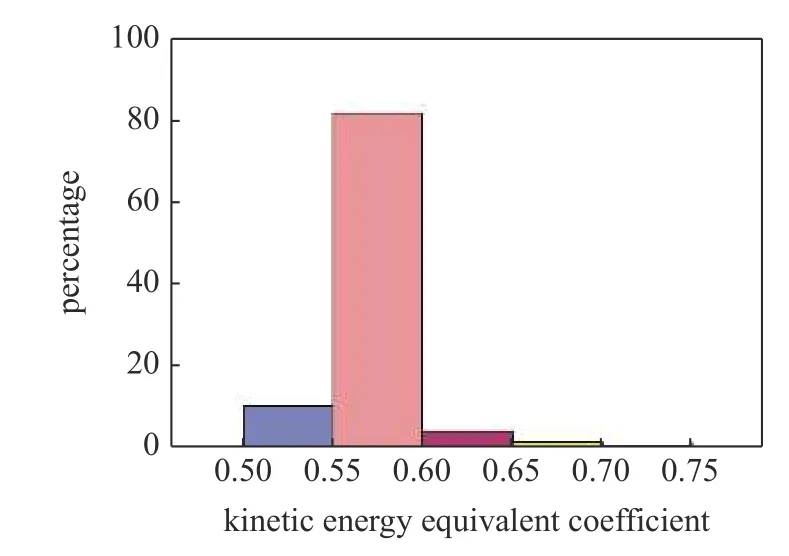
圖15 概率條形圖Fig.15 Probability bar

接著,以積分動能 K 為橫坐標,以質心動能Kβ為縱坐標繪制散點圖,如圖16 所示,顯然散點數據大致散落在某直線附近,然后對數據進行最小二乘擬合,擬合結果為一條過原點的直線,從上面的分析可以看出該直線斜率的物理意義即為 ξ .

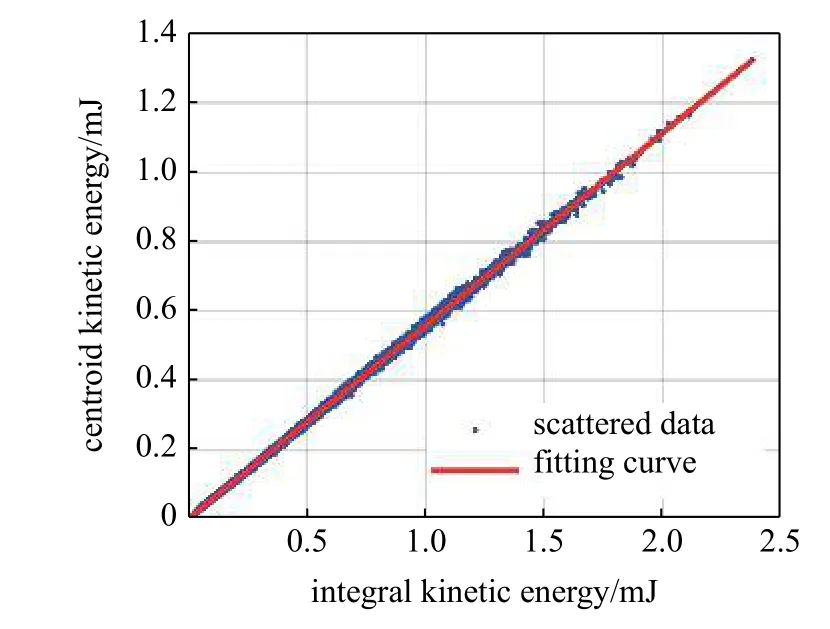
圖16 積分動能與質心動能比值關系擬合曲線Fig.16 Fitting curve of the ratio between integral kinetic energy and center-of-mass kinetic energy

由此可見將軟體機械臂的質量等效為位于質心處的集中質量所計算得到的質心動能 Kβ與實際的連續分布質量所計算得到的積分動能 K 是不相等的,但是二者的比值近似為一定值 ξ,將該定值稱為動能等效系數,為了補償二者的不等,引入基于質心的等效質量mβ,并且使mβ=m/ξ,如此,便可近似認為 Kβ≈K,從而使得基于質心所得的動能在能量上與分布式積分方法所得動能匹配起來.

綜上分析,基于質心集中質量模型的軟體機械臂拉格朗日函數為 Lβ=Kβ-Pβ,其中 Kβ由式(28)得到,.最終,將軟體機械臂的質量等效為位于質心的集中質量模型的動力學方程以矩陣形式可以寫為

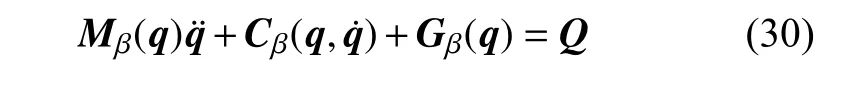
3 數值仿真算例

本小節對上述建立的軟體機械臂動力學模型進行數值仿真分析,動力學仿真參數參考文獻[32],如表2 所示.

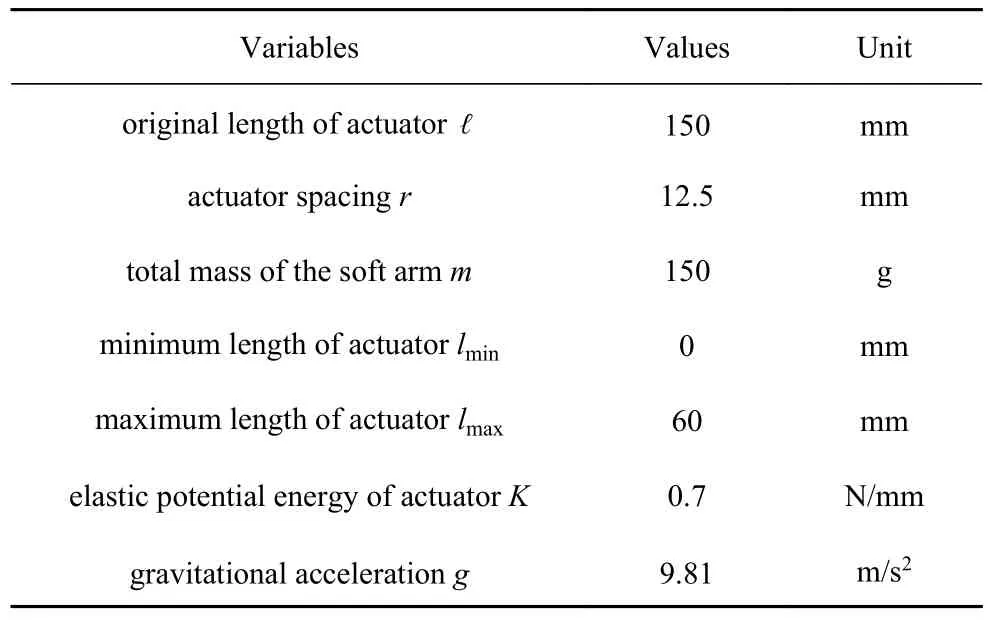
表2 動力學仿真數值Table 2 Parameters used in the dynamic simulation

3.1 純伸長模擬

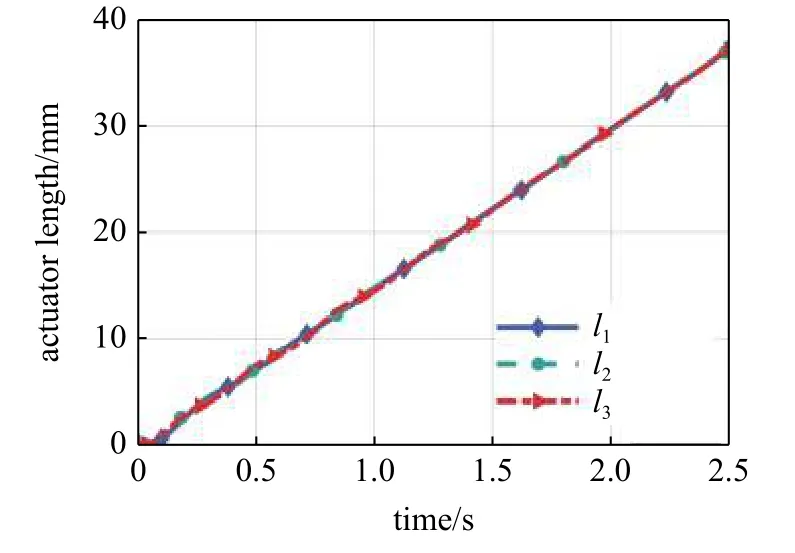
圖17 驅動器長度變化曲線Fig.17 Actuator length

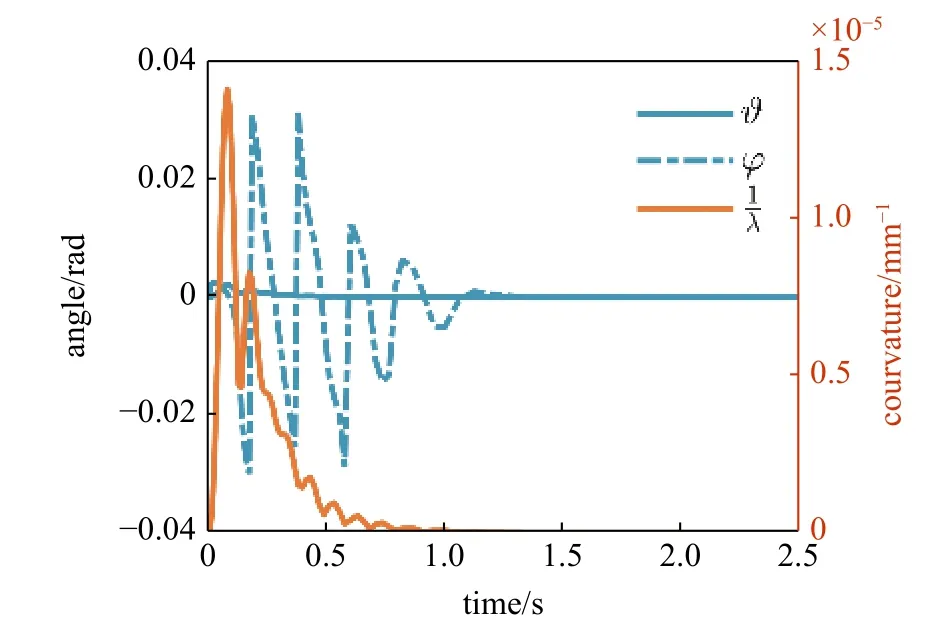
圖18 配置空間變量變化曲線Fig.18 Configure space variables

3.2 計算效率比較

為了定量比較動力學建模過程使用的兩種方法(即采用分布質量建立的積分動力學模型以及將質量等效成位于軟體機械臂質心的集中質量動力學模型)的數值計算結果與計算效率,對相同輸入條件下兩種動力學模型的求解結果以及數值仿真時間進行比較.圖19 表示的是采用分布質量的積分動力學模型求得的結果,圖20 是采用基于質心的集中質量動力學模型所求結果,比較圖19 和圖20,可以發現二者的求解結果一致,但使用兩種方法所用的時間卻大不相同,表3 給出了相同條件下兩種動力學模型的計算時間,結果表明基于質心的集中質量模型的求解效率比分布質量模型提高了大約8 倍.

表3 兩種動力學模型的計算效率比較Table 3 Comparison of computational efficiency of the two models

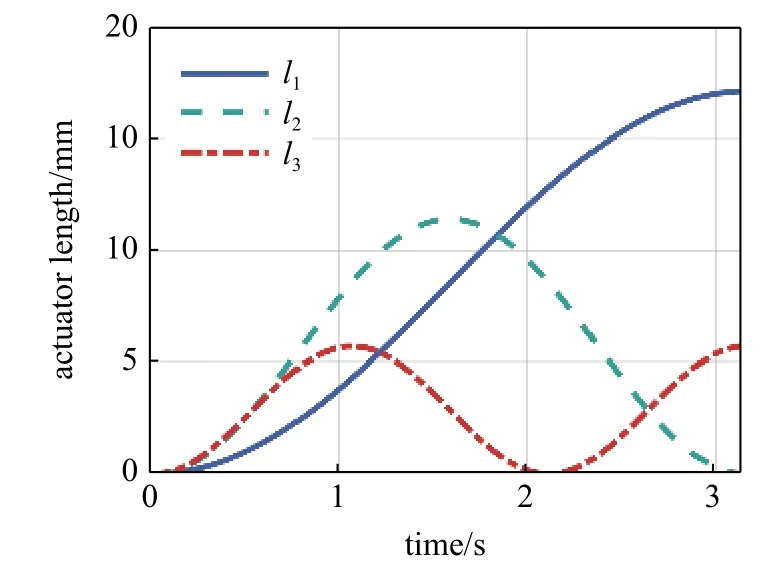
圖19 分布質量模型響應曲線Fig.19 Responses from distributed mass model

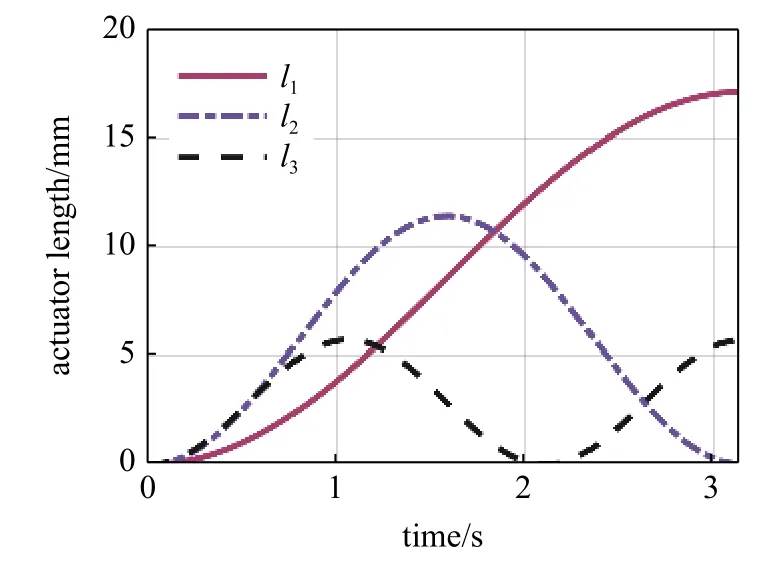
圖20 基于質心的集中質量模型響應曲線Fig.20 Responses from concentrated mass model based on mass center

分析其原因在于本文所提出的基于質心集中質量動力學模型的主要優點是它不需要可積項乘積的預積分.例如,式(14)必須預先通過對中性軸上任意點對位置求導得到速度雅可比矩陣Jυ,而該矩陣是含有積分變量η的函數矩陣,這必然會導致(Jυ)TJυ是關于積分變量η更加復雜的矩陣,然后對η積分后才能得到動能.與之相反的是,使用基于質心的集中質量模型恰好避免了這一復雜的積分計算,這是因為式(25)是預先對積分變量η進行積分,顯然這一步的積分運算是簡單的,其后再求速度并計算動能,顯著降低了計算的復雜性.

4 結論

本文以一類具有常曲率彎曲與伸長能力的軟體機械臂為研究對象,對其空間運動學及動力學建模與仿真進行了研究,主要研究結論如下.

(1) 本文采用模態方法對軟體機械臂進行運動學描述,該方法以多項式函數描述軟體機械臂的變形場,能夠簡便地推導出精確、無奇異且唯一的模態變換矩陣,該方法在沒有使用中間變換或曲線參數的情況下,直接以驅動關節變量推導軟體機械臂運動學方程.仿真結果表明該方法既能有效模擬軟體機械臂的彎曲行為,又可以模擬軟體機械臂的純伸長運動,不需要將純伸長運動狀態單獨考慮,有效克服了以往模型假定軟體機械臂變形后曲率不為零(只能模擬彎曲變形,而不能模擬直線運動)的局限性.

(2) 軟體機械臂動力學建模時,轉動動能計算復雜,影響動力學方程的求解效率,但與平動動能相比,在給定條件下,轉動動能占總動能的百分比不超過3%,其對動力學結果影響很小.因此在動力學建模過程中可以忽略,進而提高動力學方程求解效率,為軟體機械臂的實時動態控制奠定了理論基礎.

(3) 本文提出的基于質心集中質量動力學模型,將軟體機械臂的連續分布質量模型等效為位于質心的集中質量模型,利用統計的方法計算出動能等效系數,進而通過動能等效系數實現兩種模型的動能匹配.仿真結果表明,本文所建立的模型既具有分布質量模型的準確性,又具有集中質量模型的計算高效性,能夠準確、高效地獲得軟體機械臂的動力學特性.