擾動輸入時偏差傳遞函數計算方法探討

張甲英 肖美玲

（湖南交通工程學院高科技研究院 湖南·衡陽 421001）

在自動控制原理的教學當中，傳遞函數是一個非常重要的概念，計算給定輸入信號的閉環傳遞函數相對容易，而當計算系統輸出對擾動信號的傳遞函數時，一般需要對系統框圖進行等效變換。計算擾動輸入時的閉環傳遞函數或相對于擾動的偏差傳遞函數時，假設給定輸入信號為0，并將系統框圖變換為類似于計算給定輸入信號時的傳遞函數的圖形，以方便計算。但在框圖等效變換過程中，需要把綜合節點變換為一個環節或使信號符號發生變化，對原框圖變化較大。本文將綜合節點變換為一個反相器環節，而對其他環節都不做任何變更，可簡化系統變換過程，而且物理意義明確，并在此情況下研究系統對擾動輸入時傳遞函數的計算方法。

1 求取系統傳遞函數的一般方法

控制系統的分析，是通過系統的相關傳遞函數進行的。系統的結構圖往往是比較復雜的，因此，難于直接求出系統的各種傳遞函數。于是在求取傳遞函數之前，一般都進行結構簡化，得到如圖1所示的“典型結構”后，才能容易求出相關的傳遞函數[1]。在圖1的典型結構中，R(s)是給定輸入信號，B(s)為主反饋信號，E(s)為偏差信號，Y(s)是系統的輸出信號，N(s)為擾動輸入信號，G1(s)、G2(s)是前向通道的傳遞函數，H(s)為反饋通道傳遞函數。

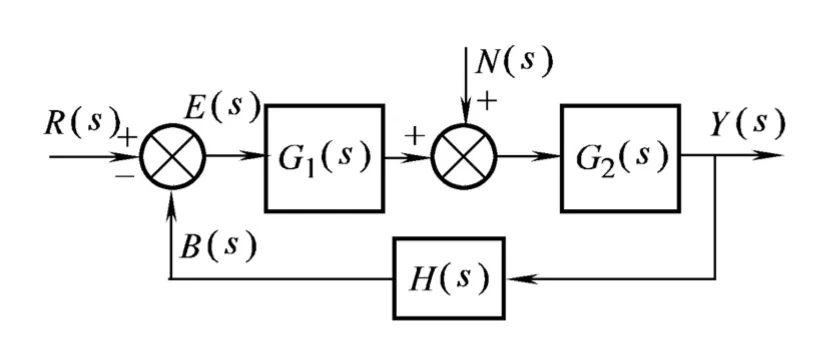
圖1：系統的典型結構圖

對應圖1結構圖，給定輸入作用下系統的閉環傳遞函數(擾動輸入N(s)=0時)為：

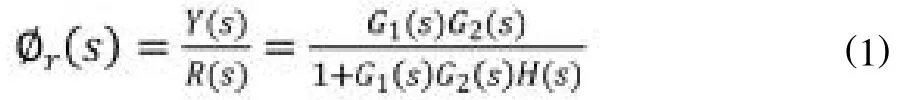
2 反相器環節的引入

由于自動控制原理課主要討論的是單輸入單輸出的關系，所以在求取擾動輸入作用下的傳遞函數時，都假設給定輸入信號為0，即R(s)=0，在此情況下研究擾動輸入時閉環傳遞函數和偏差傳遞函數。擾動輸入單獨作用下系統典型結構圖如圖2所示。對于此種情況，有的教材沒有詳細的推導過程，直接給出擾動作用下的偏差傳遞函數[1]，學生理解起來還是比較困難的。在此，本文引入一個反相器環節，可將此結構圖變換為如圖1所示的典型結構圖樣式，然后再利用類似(1)式的計算方法，即可很方便的求得擾動作用下的系統閉環傳遞函數。

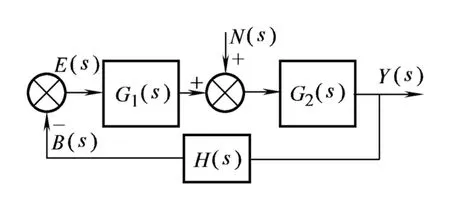
圖2：擾動輸入單獨作用下系統典型結構圖

由圖1可知，E(s)=R(S) B(S)，當R(S)=0時，

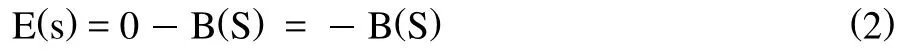
也就是說，此時E(s)與B(s)信號相反，信號從B(s)到E(s)相當于經過一個反相器，他們的傳遞函數G0(s)可通過式(2)求得，即：

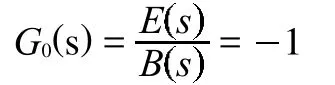
即反相器環節相當于一個傳遞函數為-1的環節。

因此，可將圖2變換成類似于圖1那樣的典型結構圖，結果如圖3所示。在變換過程中，只是把一個綜合相加點換成反相器(-1)環節，而其他環節、信號流向以及信號正負號都不變，然后利用前向通道傳遞函數、反饋通道傳遞函數的概念，很容易的求得擾動作用下的系統變換傳遞函數。

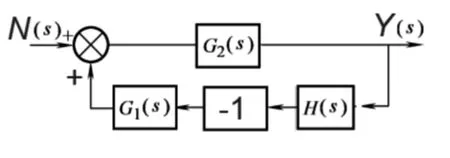
圖3：擾動輸入作用下偏差輸出的結構圖

根據圖3，擾動作用下系統的閉環傳遞函數可安下式計算：

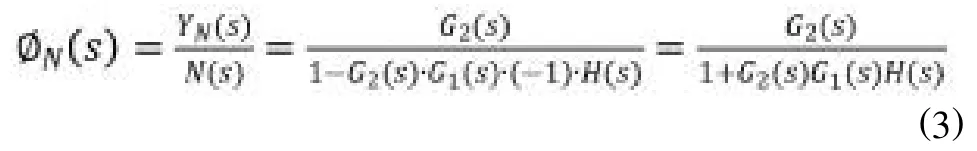
計算結果與資料[1]相同。

3 -1環節的應用

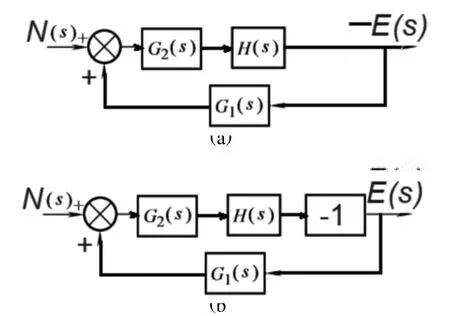
圖4：擾動作用下偏差輸出的等效變換結構圖

圖4(a)在等效變換過程中，E(s)的符號發生了變化，原圖中的E(s)變為-E(s)，有的學生理解有困難，在求取傳遞函數時，信號的符號也需要細致的處理，難以直接求得相對應的傳遞函數。而圖4(b)除了將綜合節點變換為反相器(-1)環節外，結構圖中的其他信息都沒有改變。按照圖4(b)很容易的求得擾動作用下的偏差傳遞函數：

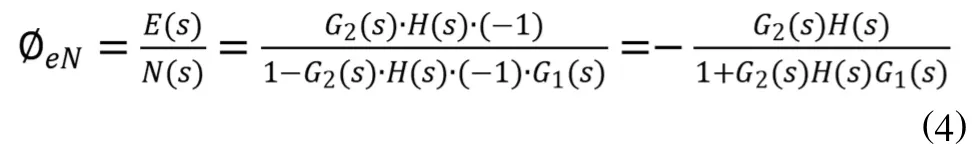
計算結果同資料[1][2]。

4 -1環節合理性討論

在計算擾動作用下系統的閉環傳遞函數或偏差傳遞函數時，假設給定輸入信號為0，即R(s)=0，這樣就會使E(s)=R(s) B(s)=0 B(s)= B(s)，根據此公式，從理論上講，偏差信號E(s)就相當于反饋信號B(s)的反向得到的，因此，用反相器(-1)環節代替綜合環節（相加）在理論上是合理的，有理論基礎。

在實際的結構圖等效變換過程中，只是用反相器(-1)環節代替綜合環節(相加)，而結構圖的其他各部分都沒有發生變化，變換過程也相對簡單。

變換后的圖形簡單，概念清晰，計算方法相對簡單，學生容易理解，結果也是正確的。

綜上所述，采用反相器環節(-1)，代替綜合環節(相加)是合理可行的方法。

5 結論

在自動控制原理的教學當中，計算擾動輸入時的閉環傳遞函數或相對于擾動的偏差傳遞函數是一個重要內容。本文在對系統框圖進行等效變換過程中，引入反相器(-1)環節，可使變換過程變得相對簡單，概念清晰，計算傳遞函數相對簡單。引入反相器環節(-1)，在理論上是合理的，實際變換過程簡單，計算結果正確，是合理可行的方法。