基于K近鄰算法的來波方向估計方法
陳 中,王杰貴,唐希雯,楊 航
(國防科技大學電子對抗學院,安徽 合肥 230031)
0 引言
來波方向(direction of arrival,DOA)估計是目標定位、輻射源識別、威脅等級判定以及有效實施干擾的基礎和前提,對于現代電子戰具有非常重要的意義。隨著電子對抗偵察裝備的發展和更新換代,信號處理任務越來越復雜,對波達角估計的要求也越來越高,如高精度、高分辨率、實時性和智能化等。
目前常用的來波方向估計方法可以分為四種:1) 基于振幅法測向的算法:常見的有最大信號法測向、比幅法測向[1]、振幅和差法測向、羅特曼透鏡法測向等;2) 基于時延相位的算法:典型代表為相位干涉儀測向[2];3) 基于空間譜估計的算法:多重信號分類(MUSIC)算法[3]測向和旋轉不變子空間(ESPRIT)算法[4]等;4) 基于機器學習[5]的算法:徑向基函數(RBF)神經網絡[6]、BP神經網絡[7]和支持向量機(SVM)[8]等。利用機器學習的方法進行來波方向估計,實現高精度、實時化和智能化的波達角估計是近年來波達角估計方法研究的熱點。
振幅法測向和相位干涉儀測向只適用于特定結構的天線陣列,空間譜估計算法計算量過大、實時性差,難以滿足實際運用的需要,而RBF神經網絡、BP神經網絡和支持向量機的算法復雜度明顯高于KNN算法。
針對上述問題,本文利用信號的相位和幅度信息作為K近鄰[9](k-nearest neighbor,KNN)算法模型的輸入數據,信號的來波方向[10]作為輸出特征,實現對于任意天線陣列高精度、實時化的來波方向估計。
1 K近鄰算法
K近鄰算法是機器學習領域的一種常用算法,能夠有效處理分類和回歸問題,在數據分類和數據挖掘中獲得了廣泛應用。KNN算法結構清晰易于實現,模型訓練時間復雜度低,不需要訓練產生額外的參數作為輔助決策,適用于來波方向估計。通過計算待分類樣本與樣本空間中所有樣本的距離,找出K個距離值最小的點,這K個點就是樣本點的K個最近鄰,根據K個最近鄰的類別歸屬情況來判斷待分類樣本所的類別,出現次數最多的類別作為分類結果。KNN的原理如圖1所示,利用K近鄰算法判斷黑色方塊的類別,當K=3時,與黑色方塊距離較近的3個對象中,有2個紅色圓點,所以黑色方塊與紅色圓點為同一類別;當K=5時,與黑色方塊距離較近的5個對象中,有3個藍色三角,所以黑色方塊與藍色三角為同一類別。
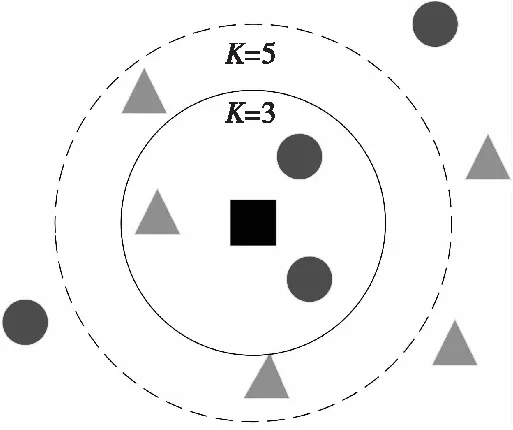
圖1 K近鄰算法原理圖Fig.1 K-nearest neighbor algorithm schematic diagram
K近鄰算法分類結果的準確性取決于樣本分布特性、K的取值和距離度量的定義。當待分類樣本分布均勻時,分類準確率較高,對訓練數據進行預處理,剔除與其他數據存在嚴重差異的數據,可以有效提升分類準確率。從圖1可以看出,K值不同,分類結果可能存在巨大差異,可以選取多個K值,統計分類結果,然后結合分類任務的實際需要,選取合適的K值。距離是衡量不同樣本間差異的一種方法,通常選用歐氏距離進行計算,在具體計算時,要選取不同樣本存在明顯差異的屬性,并為不同屬性設置不同的權重。假設一個樣本x用特征向量[a1(x),a2(x),…,am(x)]來表示,其中ar(x)表示隨機樣本x的第r個屬性。那么,對于兩個樣本xi和xj來說,距離可以定義為:
(1)
式(1)中,wr為不同屬性的權重。
2 基于K近鄰算法的來波方向估計方法
基于K近鄰算法的來波方向估計方法主要優勢有兩點:一是新的特征提取方法能夠使用于任意天線結構;二是構建基于K近鄰算法的來波方向估計模型,能夠極大地提升來波方向估計的準確性、實時性和智能化水平。
2.1 特征提取
通過數字化處理,提取各陣元采樣信號的頻率、幅度和相位等特征信息,作為K近鄰算法估計模型的輸入數據。
對采樣信號進行預處理,然后做FFT變換,獲取采樣數據的頻率、相位差等特征信息,作為KNN波達角估計的輸入數據。設某一路采樣信號為:
x(n)=A0exp[j(2πfnts+φ0)]+v(n),n=0,1,…,N-1
(2)
式(2)中,A0為信號振幅;f為接收信號頻率;φ0為信號初始相位;ts為采樣間隔;N為采樣點數;v(n)為接收機內部噪聲,假定為高斯白噪聲。
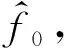
(3)
式(3)中,ts為采樣時間間隔,即采樣率的倒數;N為采樣數。
接收天線第i個陣元收到的信號為si′(i=0,1,…,K-1),其中K為陣元個數,則作相參積累后得到的最終信號:
(4)
接收天線第i個陣元和第j個陣元接收到的信號相位差為:
φij=arg{Si·Sj*}
(5)
多元陣測向系統的天線陣列結構多種多樣,如比幅法測向系統通常采用均勻圓陣列,相位干涉儀測向系統的天線陣元間距需要符合一定的比例,傳統的DOA估計方法只能處理某一類的天線陣列,而本方法可以適用于所有天線陣列結構。
2.2 基于K近鄰算法的來波方向估計模型
基于K近鄰算法的來波方向估計方法是將來波方向估計問題轉化為分類問題,將信號入射范圍分為若干個類別,訓練集中包含每個類別的若干個樣本,計算待分類樣本與訓練集中所有樣本的距離,統計距離最小的K個樣本,K個樣本中出現頻率最高的類別就是待分類樣本的類別,而該樣本的類別就是信號的來波方向,其流程圖如圖2所示。
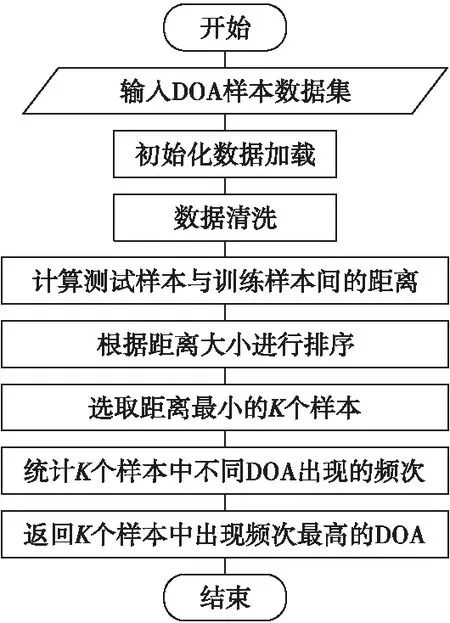
圖2 基于K近鄰算法的來波方向估計模型流程圖Fig.2 Flow chart of incoming wave direction estimation model based on K-nearest neighbor algorithm
將0°~360°的信號入射范圍分為1°,2°,…,360°等360個類別,訓練集中包含每個類別的100個樣本,共3.6×104個樣本,計算待分類樣本與訓練集中所有樣本的距離,即可得到信號來波方向,DOA估計精度為1°。在信號入射范圍相同的情況下,DOA估計精度越高,類別越多,計算復雜度越高。
3 仿真與分析
以6陣元線形天線為例,相鄰陣元間的距離之比為3∶5∶7∶11∶17,改變來波信號的頻率和信噪比,生成基于不同頻率、不同信噪比和不同波達方向的樣本數據集,進行對照實驗,通過統計不同條件下的來波方向估計的準確率,檢驗基于K近鄰算法的波達角估計方法的實際效果。
利用均方根誤差(RMSE)和估計準確率兩個可視化標準衡量基于KNN的來波方向估計方法的性能,均方根誤差是估計值與真實值之差的平方與測試次數比值的均方根,計算公式為:
(6)
式(6)中,θe為DOA的估計值,θt為DOA的真實值,m為測試次數。
估計準確率為估計誤差小于估計精度的比例,計算公式為:
(7)
式(7)中,Δθ為DOA估計精度。
3.1 不同DOA估計精度下的估計準確率
運用基于K近鄰算法的來波方向估計方法進行來波方向估計時,估計精度由訓練樣本集中來波方向的步進決定,生成不同估計精度的訓練樣本集,觀察來波方向估計準確率的變化情況。訓練樣本的頻率為10 GHz,信噪比為5 dB,信號來波方向為-50°~50°,步進分別為0.1°、 0.5°、 1°,每個來波方向隨機產生50個信號樣本,訓練樣本集分別包含50 000、10 000、5 000個訓練樣本;測試樣本的頻率分別為10 GHz,信噪比為5 dB,信號來波方向為1°~5°,步進為0.1°,隨機產生包含每個來波方向的測試樣本集。不同來波方向估計精度下的來波方向估計準確率如圖3所示。
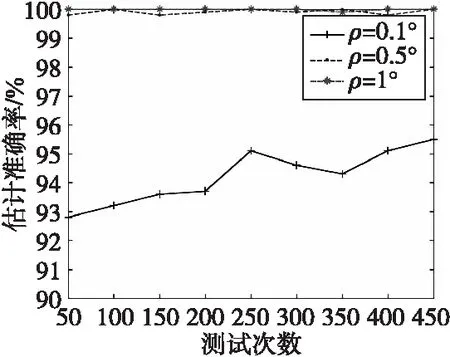
圖3 不同頻率估計精度下的來波方向估計準確率Fig.3 Estimation accuracy of direction of arrival under different frequency estimation accuracy
從圖3可以看出,當來波方向估計精度為0.5°和1°時,估計準確率均在99.8%以上,當來波方向估計精度為0.1°時,估計準確率也在92.8%以上,能夠滿足實際需要,這說明本方法能夠實現高精度的來波方向估計。
3.2 不同頻率估計誤差下的估計準確率
運用相位干涉儀測向方法進行來波方向估計,信號頻率為10 GHz,信噪比為5 dB,信號來波方向為0°~50°,步進為1°,每個來波方向隨機產生100個信號樣本,共5 000個樣本,然后在頻率估計誤差分別為10、 300、 600 MHz的情況下進行來波方向估計,計算均方根誤差,不同頻率估計誤差下的均方根誤差如圖4所示。
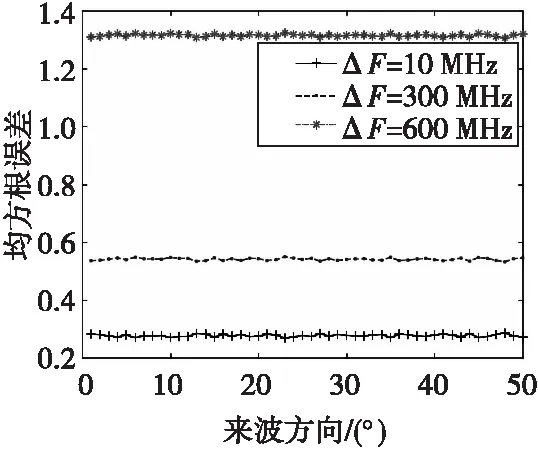
圖4 不同頻率估計誤差下的均方根誤差圖Fig.4 Root mean square error under different frequency estimation errors
從圖4可以看出,當頻率估計誤差ΔF=10 MHz時,均方根誤差在0.28左右浮動;當頻率估計誤差ΔF=300 MHz時,均方根誤差在0.54左右浮動;當頻率估計誤差ΔF=600 MHz時,均方根誤差在1.31左右浮動。隨著頻率估計誤差的增大,相位干涉儀測向的精度下降非常明顯。
運用基于K近鄰算法的來波方向估計方法時,訓練樣本的頻率為10 GHz,信噪比為5 dB,信號來波方向為-50°~50°,步進為0.1°,每個來波方向隨機產生50個信號樣本,訓練樣本集包含50 000個訓練樣本;測試樣本的頻率分別為10.01、 11、 12 GHz,即頻率估計誤差分別為0.01、 1、 2 GHz,信噪比為5 dB,信號來波方向為1°~5°,步進為0.1°,隨機產生包含每個來波方向的測試樣本集。不同頻率下的來波方向估計準確率如圖5所示。
從圖5可以看出,真實頻率與訓練樣本的頻率之間的差值越來越大,但來波方向估計準確率的變化并不明顯,即便是在頻率相差2 GHz的情況下,來波方向估計準確率依然在90%以上,這說明本文提出的估計方法在信號頻率估計誤差方面具有較好的魯棒性,能夠在存在嚴重頻率估計誤差的情況下進行準確的來波方向估計。
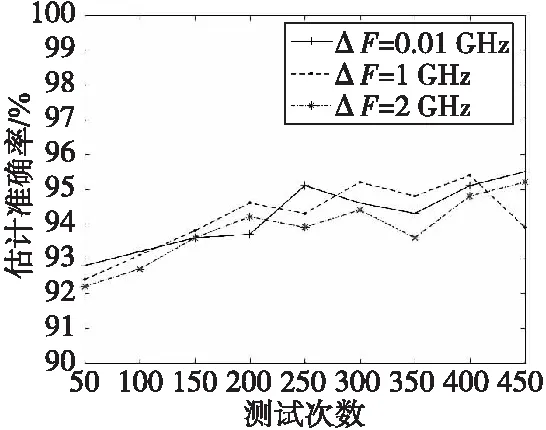
圖5 不同頻率估計誤差下的DOA估計準確率Fig.5 Estimation accuracy of direction of arrival under different frequency estimation errors
3.3 信號入射范圍對來波方向估計的影響
運用相位干涉儀測向方法進行來波方向估計,在相同的陣列天線模型和信號模型下,信號頻率分別取8、9、10、11、12 GHz,信噪比為5 dB,信號來波方向為-50°~50°,步進為1°,每個來波方向隨機產生50個信號樣本,每種頻率生成5 000個樣本,分別統計不同頻率下的均方根誤差,得到均方根誤差與來波方向間的關系如圖6所示。
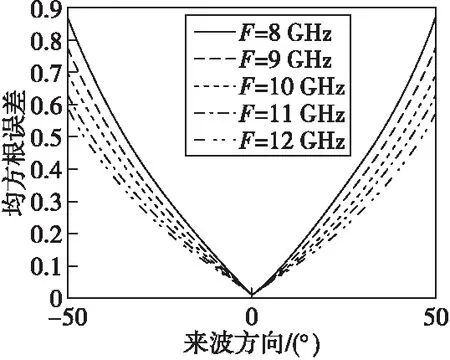
圖6 不同頻率下的均方根誤差圖Fig.6 Root mean square error plots at different frequencies
可以明顯看出,隨著入射角的范圍增大,均方根誤差明顯增大,這說明來波方向范圍越大,相位干涉儀測向方法誤差越大。
采用基于K近鄰算法的來波方向估計方法時,訓練樣本的頻率為10 GHz,信噪比為5 dB,信號來波方向為-50°~50°,步進為0.1°,每個來波方向隨機產生50個信號樣本,訓練樣本集包含50 000個訓練樣本;測試樣本的頻率分別為10 GHz,信噪比為5 dB,信號來波方向為-50°~50°,步進為10°,每個來波方向產生1 000個樣本。來波方向估計準確率隨來波方向范圍變化的情況如圖7所示。
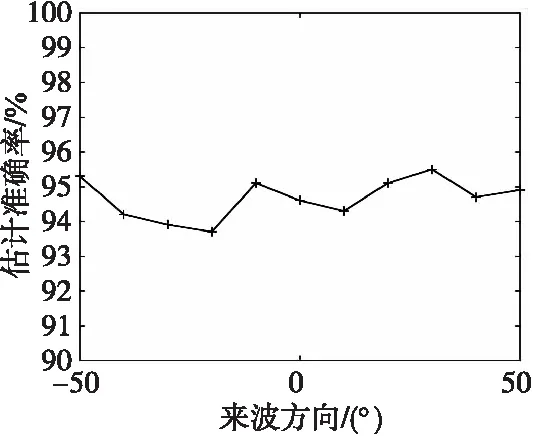
圖7 估計準確率變化圖Fig.7 Change chart of estimation accuracy
從圖7可以看出,采用基于KNN的來波方向估計方法時,不論來波方向范圍怎么變化,來波方向估計準確率始終保持在相對穩定的范圍。這說明與相位干涉儀測向方法不同,信號入射范圍的寬度對本方法的影響不大,本文方法可以穩定地對較大范圍內的來波信號的來波方向進行準確估計。
4 結論
本文提出基于K近鄰算法的來波方向估計方法,該方法提取來波信號的相位和幅度信息作為輸入數據,利用K近鄰算法構建來波方向估計模型,實現了高精度、實時化的來波方向估計。仿真實驗結果說明該方法能夠實現高精度的來波方向估計,并通過和干涉儀測向方法的對比,證明本文方法對頻率估計誤差和信號入射范圍有更好的魯棒性,進一步體現了該方法的優越性和可行性。

