基于變分模態(tài)分解的激光幕破片信號處理算法

陸治鵬，劉 吉，武錦輝，牛雅昕

(中北大學信息與通信工程學院，山西 太原 030051)

0 引言

彈丸的速度是評估彈行系數的重要參數，其結果是判斷武器性能的一項重要指標，是優(yōu)化武器的重要依據[1]。傳統(tǒng)的速度測試裝置有網靶、線圈靶、光電靶等。破片體積小、速度高、形狀不規(guī)則，散布方向任意、范圍大，且破片測試中通常環(huán)境惡劣、干擾大。為解決這些難題，改進的高速攝影、微波雷達、多光譜探測、激光靶等被廣泛應用[2-3]。其中，激光靶對于小破片速度測量有獨特優(yōu)勢，其測試精度高、靈敏度可調且可重復獲得破片的近似瞬時速度。對于破片信號的提取，由于存在振動、沖擊、火光等因素的影響，過靶信號會混疊大量噪聲信號。過靶信號中噪聲信號為不規(guī)則、非平穩(wěn)隨機高頻信號以及沖擊、振動、火光等外力因素帶來的偏移信號[4]，在時域中直接使用傳統(tǒng)方法峰值，上升沿或下降沿一半等方法取值有很大困難。此外，在頻域中使用小波變換處理時，會存在小波基的使用問題，小波變換有良好的時頻特性，可以將混雜在噪聲中的過靶信號識別出來，但不同形狀的彈丸產生的波形不同，選用不同的小波基會產生不同精度的誤差[5]。本文針對上述問題提出基于VMD的激光幕信號處理算法。

1 激光幕測速系統(tǒng)

原向反射式激光幕系統(tǒng)主要由光電探測模塊、信號調理模塊、高速數據采集裝置和主機組成[6]。如圖1所示，當破片通過光幕的有效區(qū)域時，光電探測模塊接收到的破片遮擋產生過靶信號，過靶信號通過信號調理電路放大濾波后，通過高速采集卡進行采集，將過靶信號在軟件中進行處理識別取點后，完成破片的速度測量。

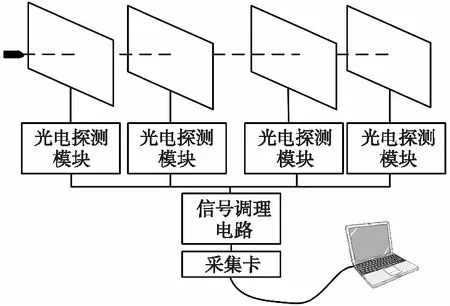
圖1 激光幕測速系統(tǒng)Fig.1 Laser screen velocimetry system

圖2所示為激光幕測速系統(tǒng)產生的過靶信號，圖中是采集到的3 mm小破片，若不對其進行處理，在時域中直接進行識別，會將圖中噪聲信號誤判為過靶信號。

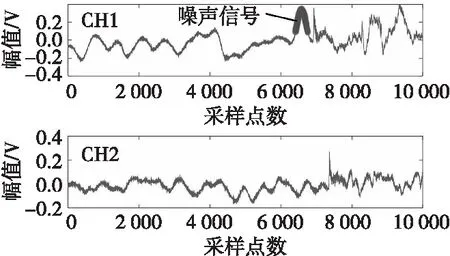
圖2 兩通道過靶信號Fig.2 Two channel target signal

2 破片信號的算法處理

2.1 變分模態(tài)分解

小破片通過激光光幕時，過靶信號為突變信號，信噪比較好的情況下，可在時域中直接對過靶信號識別，而當破片信號淹沒在噪聲中時則無法直接分析[7]。VMD將過靶信號分解成不同中心頻率的模態(tài)分量，過靶信號作為突變信號，對包含其頻率和幅值成分較多的信號進行重構，可進行降噪且利于識別。

VMD分解中通過迭代搜尋變分模型的最優(yōu)解，期間，每個固有模態(tài)函數的中心頻率和帶寬都經過交替方向更新，自適應地實現信號的頻域分離，得到K個模態(tài)分量。如下為VMD的處理過程：

假設待分解的信號f由k個中心頻率不同的IMF分量Uk構成，并且各IMF圍繞中心頻率ωk收斂，據頻移信號的高斯平滑度來估計其帶寬，使每個子信號的估計帶寬和最小。其帶約束條件的變分問題構造如下[8]：

(1)

式(1)中，Uk(t)為t時復雜信號，f(t)通過VMD分解得到的頻率不同的離散子信號，δ(t)為單位沖激函數。為了求解該變分問題的最優(yōu)解，引入式(2)：

L({uk},{wk},λ)=

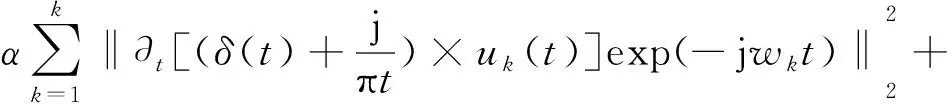
(2)

式(2)中，α為懲罰因子，λ(t)為拉格朗日乘子。

采用懲罰算子交替方向法，尋求式(2)的最優(yōu)解，按照收斂條件并應用最優(yōu)解更新每個本征模式函數Uk(t)，中心頻率ωk和λ(t)，最終將過靶信號分解成有限個模態(tài)分量。具體分解步驟如下：

1) 對式(2)中參數uk、ωk、λ和n進行初始化，n為0。

2) 設置循環(huán)過程，使得n=n+1，更新uk、ωk，求其極小值公式描述如下：

(3)

(4)

3) 乘法算子λ的更新公式如下：

(5)

式(5)中，τ表示步長更新系數。

4) 判斷分量是否滿足約束條件：

(6)

式(6)中，ε<10-6。若滿足約束條件式(6)，終止循環(huán)，獲得有限個IMF分量；如果不滿足，則返回至步驟2)，重復上述的步驟。

VMD的分解參數選取很重要，選用不合適的參數會導致過靶信號混疊在低頻部分中，導致過靶信號被當做噪聲去除掉，VMD效果主要取決于模態(tài)數K和二次懲罰因子α。模態(tài)數K是原信號經過分解所得K個模態(tài)分量，VMD預先設定分量個數減少模態(tài)混疊現象的發(fā)生；二次懲罰因子α影響分解的精度，懲罰因子越大，頻帶越窄，重構信號越集中[9]。

對過靶信號進行VMD分解結果如圖3所示。該通道信號選用的模態(tài)個數為5，帶寬參數a=2 000，分解結果如下：IMF1中振動產生的偏移信號，IMF3-IMF5中高頻噪聲均被當作模態(tài)分量很好的分解出來；過靶信號集中在IMF2中，過靶信號被當作模態(tài)分量分解出來。

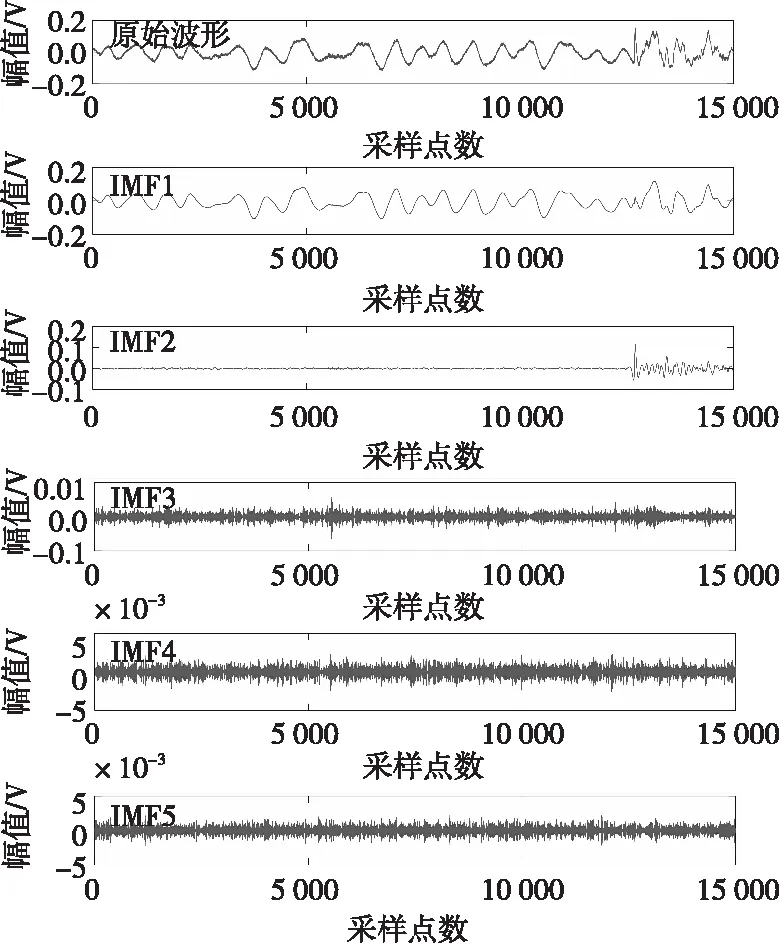
圖3 VMD分解結果Fig.3 VMD decomposition results

2.2 小波閾值處理

小波閾值去噪選用合適的小波基與分解層數對過靶信號進行處理，得到一組不同尺度的小波分解系數[10]。針對破片信號特征，除過靶信號之外，其余信號均為噪聲，硬閾值函數處理效果較好，但信號平滑性較差；軟閾值處理后信號相對平滑，但會產生固定誤差。本文使用文獻[11]中的改進閾值函數，將硬、軟閾值函數采用加權平均的方法結合起來，得到一種新的閾值函數：

(7)

式(7)中，a和b為調節(jié)因子，a=[0,1]，b>0。該閾值函數結合折中閾值函數引入了調整系數a，結合了硬閾值與軟閾值的優(yōu)點，并加入了調整因子b，改善小波系數的收縮程度。本文使用該函數完成分量中的低頻部分的濾波，增大小波系數的收縮程度，同時，用于改善多個分量還原后產生的固定誤差。

2.3 基于VMD的激光靶信號處理算法

激光幕測速系統(tǒng)通過采集卡采集過靶信號，當進行多破片識別的時候，破片的大小不確定，其過靶產生的突變信號頻率不確定，過靶信號不一定完整地分解在某一分量中，因此，需對各個分量中的結果進行判斷。判斷IMF1中閾值與其余分量中極大值點的關系，若大于閾值，則進行小波閾值去噪，否則認為其為噪聲將該分量去除[12]。處理流程如圖4所示。

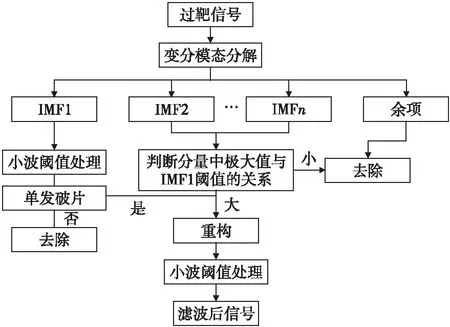
圖4 算法處理框圖Fig.4 Algorithm processing block diagram

得到重構信號后，通過峰值點識別信號中的過靶信號的特征點。對于單發(fā)小破片，直接提取波形的最大值點。對于破片測試，將分量中的低頻部分去除，其余分量與低頻部分的閾值進行判斷后重構，對重構信號進行極大值取點，依據先入先出原則進行速度計算。

3 仿真及結果處理

3.1 濾波信噪比結果對比

在某靶場進行3 mm預制破片試驗，試驗現場如圖5所示。分別用小波變化、EMD分解以及VMD分解的方法進行處理過靶信號，小波變化選用“db4”小波，分階層數為5；EMD去除前兩層高頻分量；VMD分解層數為5，去除兩層高頻分量，可得其信噪比(SNR)結果如表1所示。

圖5 試驗現場Fig.5 Experimental site

信噪比值越大說明該方法降噪越好，對比表1結果可得，VMD分解的信噪比優(yōu)于EMD和小波處理的結果，其去除高頻噪聲的效果更好。

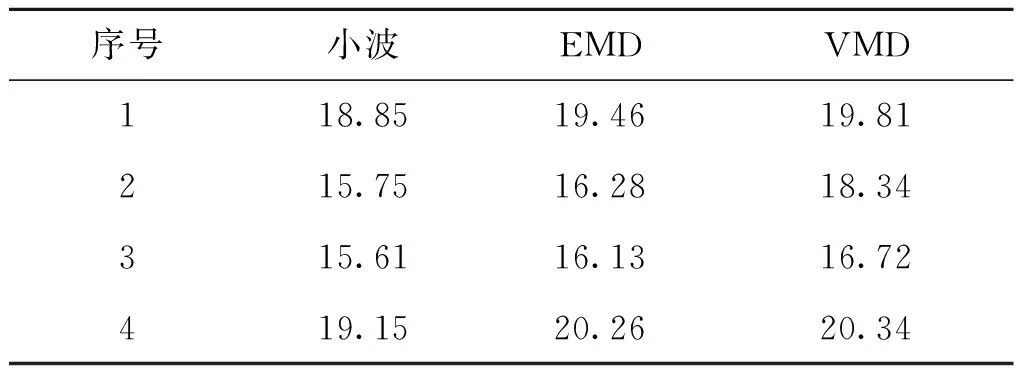
表1 信噪比對比Tab.1 Signal to noise ratio comparison

3.2 單發(fā)3 mm破片速度計算

對圖5試驗現場獲得的過靶波形進行處理，如圖6所示。圖6(a)、(b)分別為光幕靶第一通道和第二通道的波形圖，過靶波形為3 mm破片通過獲得的原始信號，處理后波形為使用該算法的處理結果，由圖可知，破片的過靶信息被提取出來。

圖6 過靶信號處理前后對比Fig.6 Comparison before and after target signal processing

獲得過靶波形后，依據過靶波形計算破片速度，如表2所示。由表可知，相較于手動選擇區(qū)域中的峰值點，本文算法不僅可以完成自動識別，且其求得的平均誤差更小，對于單發(fā)高速小目標的速度提取有一定參考意義。

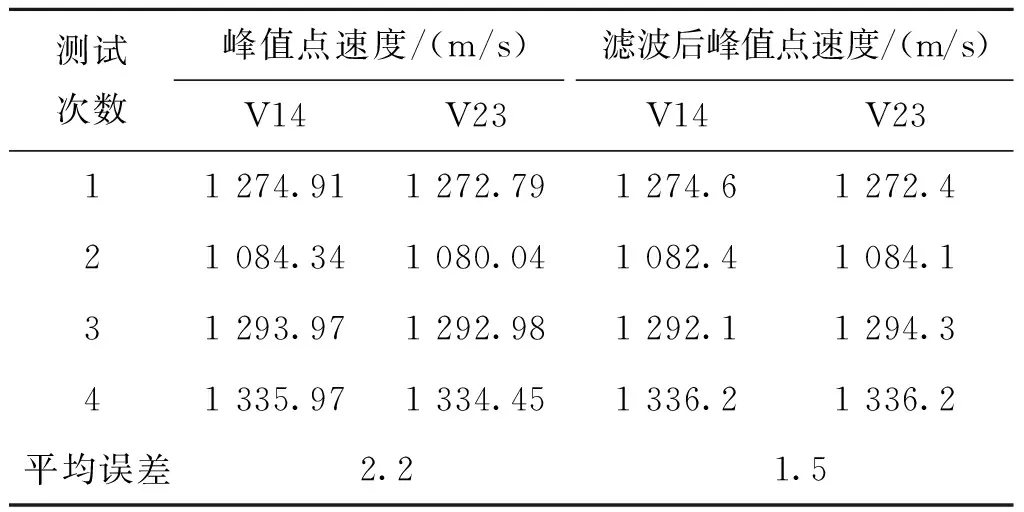
表2 單發(fā)3 mm破片計算Tab.2 Calculation of single shot 3 mm fragment

3.3 多發(fā)小破片處理結果

將本文方法應用于破片識別，由于破片的數據量較大，為得到更多頻率信息，將模態(tài)數設置為7。同時將分解后的IMF1分量直接去除，將分解后的模態(tài)分量IMF3-IMF5進行重構后進行劃分閾值的極大值點識別，閾值選用0.27，其VMD分解重構后以及其處理后拾取率如表3所示。

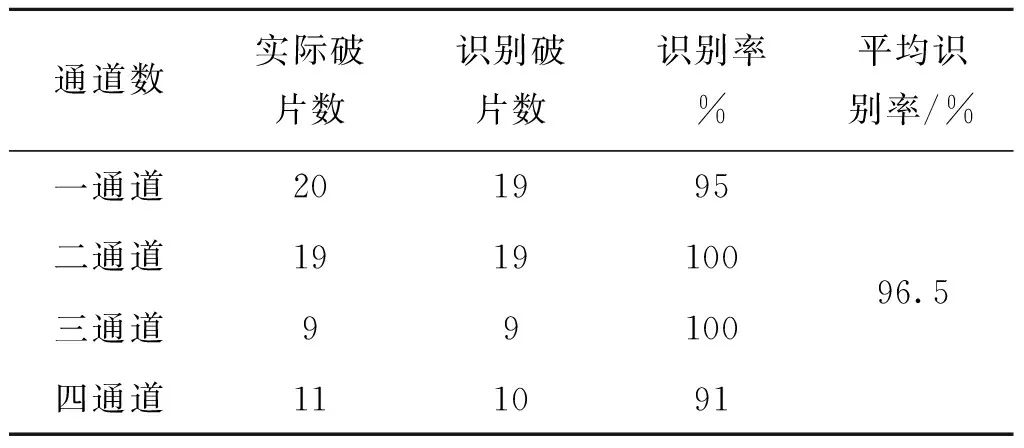
表3 多發(fā)破片拾取率Tab.3 Pick up rate of multiple fragments

四個通道中的部分處理效果圖如圖7所示。上圖為初始的過靶信號，下圖為使用本文算法處理后的波形圖。由圖7可知，破片的過靶波形均被成功提取出來，再使用極大值法提取過靶的峰值點，依據先入先出原則對兩靶的峰值點對應進行速度計算，由經典速度計算公式v=s/t可得速度結果如表4所示。

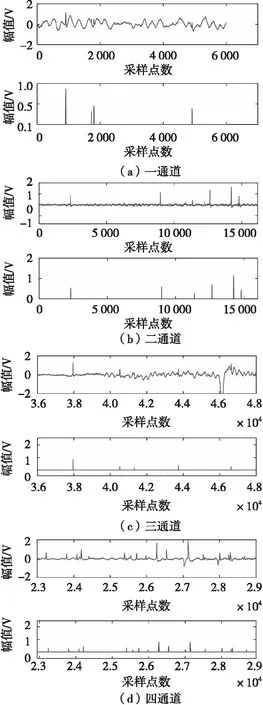
圖7 破片處理效果Fig.7 Fragment processing effect

表4 多發(fā)破片速度計算Tab.4 Velocity calculation of multiple fragments

4 結論

本文提出基于變分模態(tài)分解的激光幕破片信號處理算法，該算法使用VMD將破片過靶信號分解成不同中心頻率的模態(tài)分量，再對低頻部分進行小波閾值處理并進行衰減或去除，其余分量與低頻部分閾值進行判定后進行濾波或者去除，最后將剩余分量重構，進而依據先入先出原則對光幕進行取點之后再計算速度。實驗結果表明：該方法較小波閾值濾波相比信噪比提高了8.7%；特征點提取的平均誤差降低了31%；目標的拾取率達到96.5%。該算法對于小破片的自動濾波識別具有一定的參考意義。但對于兩光幕各自的破片匹配，提升其自動處理的識別率和準確率，仍需進一步改進和研究其處理算法。VMD算法可應用于軸承故障檢測、語音增強、地震信號去噪等方面，本文算法對于這些領域的信號處理亦有參考意義。