HPM課例研究中的教學研討主題

汪曉勤

(華東師范大學教師教育學院 200062)

近年來，HPM課例研究的對象逐漸由單一的新課擴展到單元教學、復習課教學，教師對于數學史料的需求日益增加；而隨著HPM課例的涌現，他們對于教學設計創新性的要求也在不斷提高.HPM課例研究包含“選題與準備”“研討與設計”“實施與評價”“整理與寫作”四個環節，其中，“研討與設計”環節是課例成敗的關鍵，若研討的方向不明確，效果勢必會大打折扣.

另一方面，在后疫情時代，網絡研修業已成為教師專業發展的重要途徑之一.來自不同地區、不同學校、具有不同教育背景和不同教齡的一線教師和高校研究者定期相聚云端，針對同一主題的教學設計開展深入的研討，這種無門檻、無費用、便利高效的教研形式深受那些有強烈學習動機的教師的歡迎，但如何讓教師在網絡研修中真正有收獲，是組織者需要深入思考的問題.

“內容呈現”和“認知需求”是HPM課堂教學評價的重要指標，前者指的是數學史料的科學性、可學性、有效性、人文性和趣味性，而后者指的是數學史料的運用方式，也就是教師在教學中“用什么數學史料”和“如何用數學史料”的問題.本文以HPM網絡研修的若干知識點為例，初步呈現教學研討的一個內容框架.

1 追本溯源

HPM視角下數學教學的基本理念是“再創造”，即讓學生親歷知識的發生和發展過程.數學史可以幫助教師在課堂上構建“知識之諧”，營造“探究之樂”，實現“能力之助”，為此，教師需要以數學史為參照系設計探究活動.因此，數學主題的源與流理應成為教學研討最重要的內容.

以滬教版高中數學新教材中的“三角不等式”為例.該主題與正負數運算法則息息相關.眾所周知，我國是世界上最早認識并應用負數的國家，漢代數學典籍《九章算術》“方程章”中提出了世界上最早的有理數四則運算法則，其中，非零兩數的減法法則為“同名相除，異名相益”，非零兩數的加法法則為“異名相除，同名相益”.雖然中國古代數學家沒有明確提出“絕對值”的概念，但這里的“相益”說的就是絕對值相加，“相除”說的就是絕對值相減.設有兩數

a

和

b

，若

ab

>0，則若

ab

<0，則|

a

-

b

|=|

a

|+|

b

|，|

a

+

b

|=

中國古代數學家尚未將數系從有理數擴充到實數，但上述運算法則顯然也適用于實數.因此，對于任意非零實數

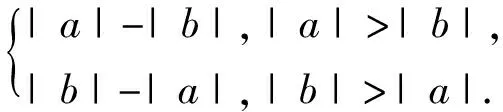
a

和

b

，絕對值不等式|

a

±

b

|≤|

a

|+|

b

|均成立.當

a

或

b

等于零時，上述不等式顯然也成立.因此，絕對值不等式對于任意實數均成立.這里我們看到，絕對值不等式源于實數的運算，了解了這一點，我們就能理解數學史融入絕對值不等式教學的意義了.教科書將上述不等式稱為“三角不等式”，對教師起了誤導作用.例如，有的教師會從向量的不等式(真正的“三角不等式”)|+|≤||+||出發引入絕對值不等式，與絕對值不等式的歷史序相悖.事實上，A.A.Bennett于1921年首次提出關于范數的三角不等式‖

r

+

r

‖≤ ‖

r

‖+‖

r

‖.之后，數學家根據向量減法的三角形法則提出關于向量的三角不等式，如J.L.Kelley在《近世代數引論》中將向量,和之間的關系|-|+|-|≥|-|①稱為“三角不等式”(圖1)，而將不等式|+|≤||+||視為①的特殊情形；N.D.Kazarinoff在《解析不等式》中則借助復平面建立了復數

w

和

z

之間的三角不等式|

w

±

z

|≤|

w

|+|

z

|(圖2).

圖1 向量的三角不等式 圖2 復數的三角不等式

但是，實數的絕對值不等式與三角形并無關系，只因它與向量或復數的三角不等式形似，故編者采用了同樣的名稱.只有正本清源，才不會望文生義，誤入歧途.

2 想方設法

HPM視角下數學命題或公式的教學，注重命題或公式的不同證明方法，彰顯“方法之美”、實現“能力之助”，是數學史的兩類基本價值.教學設計研討的目的之一在于提供豐富的素材，打開教師的思路，拓寬教師的思維.例如，關于均值不等式，常用的方法有趙爽弦圖模型和歐幾里得半圓模型等，但還可以嘗試更多的方法，《九章算術》中的勾股容方問題可以用來構造新的幾何模型.

如圖3，在矩形

ACBR

中，

BC

=

a

，

AC

=

b

，

a

<

b

，正方形

FCED

和

VSUR

分別內接于Rt△

ACB

和Rt△

BRA

，延長

VS

，交

FD

于

T

.因

a

<

b

，故

TD

<

ST

，即于是得②或③.兩邊開方即得均值不等式④.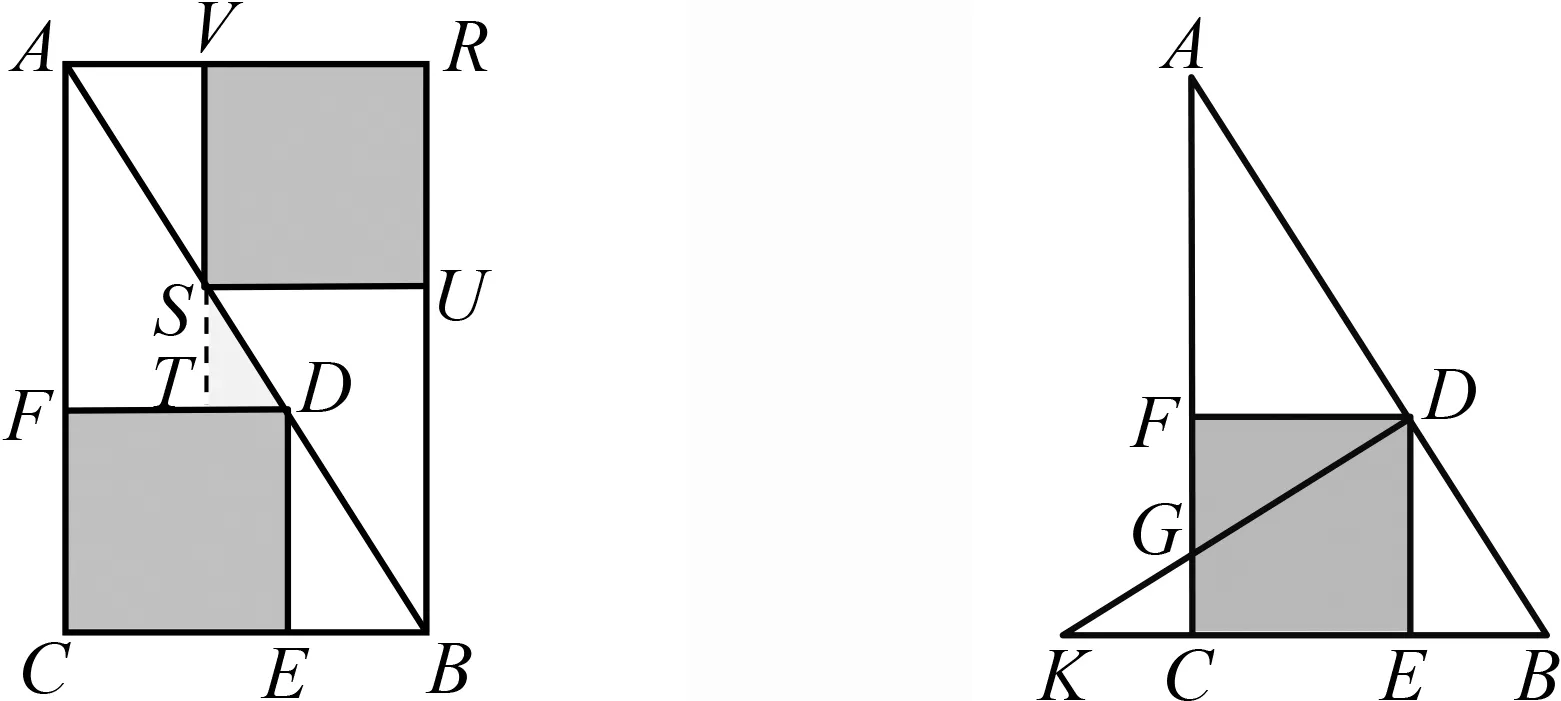

圖3 均值不等式證明之一 圖4 均值不等式證明之二

如圖4，正方形

FCED

內接于Rt△

ACB

，過

D

作

AB

的垂線，交

BC

的延長線于點

K

，交

FC

于

G

.易證Rt△

ADG

≌Rt△

KDB

，故

S

△<2

S

△，即于是同樣可得不等式②和③.如圖5，正方形

FCED

內接于Rt△

ACB

，不難證明，Rt△

ACB

內接長方形的最大面積 為

ab

，故有于是得不等式③和④.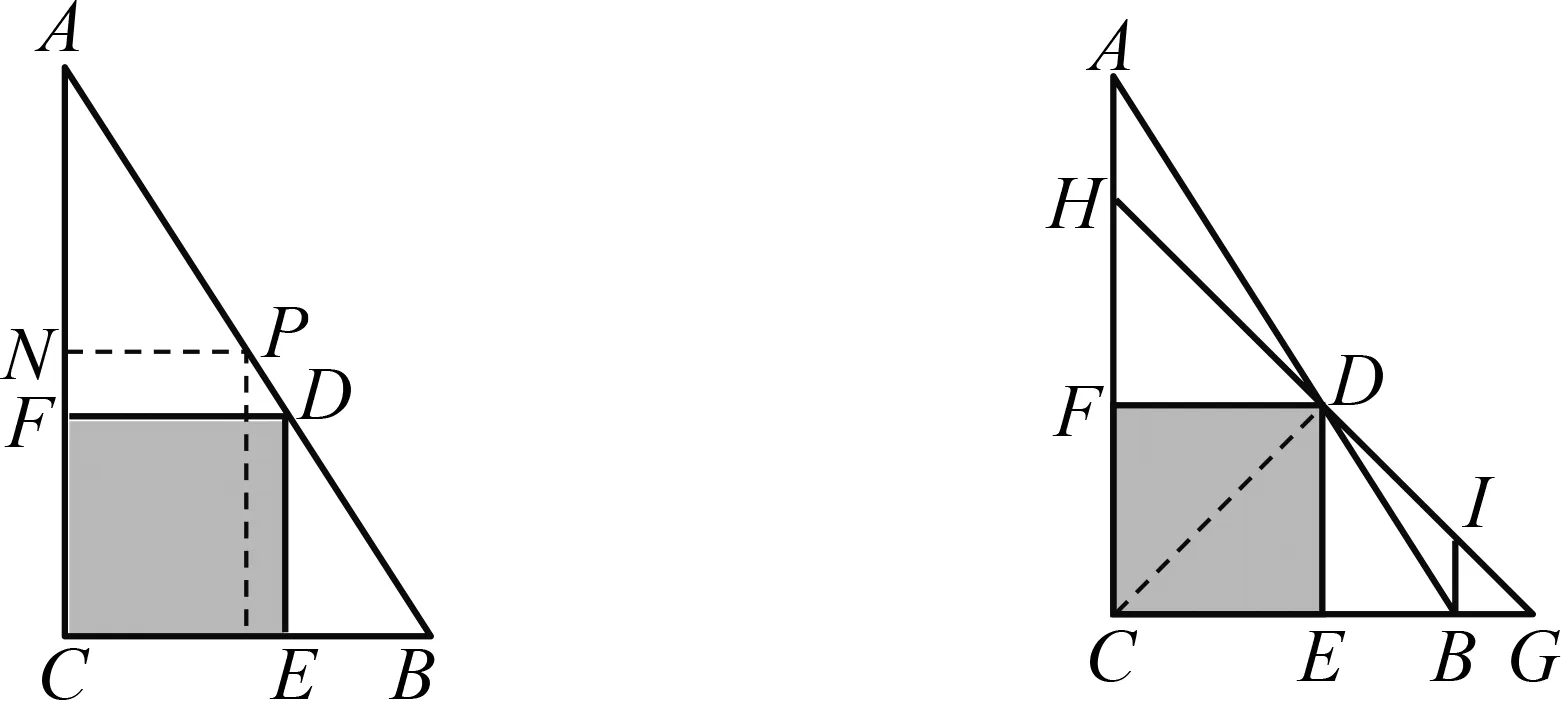

圖5 均值不等式證明之三 圖6 均值不等式證明之四

如圖6，正方形

FCED

內接于Rt△

ACB

，過點

D

作

CD

的垂線，交

AC

于

H

，交

CB

延長線于

G

，過點

B

作

CB

的垂線，交

HG

于點

I

.因

a

<

b

，故

DB

<

DA

，由△

AHD

和△

BID

的相似性知，

BG

=

BI

<

AH

，若設

EB

=

p

，

AF

=

q

(

p

<

q

)，則即于是有故得不等式如圖7，在Rt△

ACB

中，

CG

為斜邊

AB

上的高，在

CG

上作正方形

CGHI

，邊

HI

交

AC

于

J

，易知Rt△

CIJ

≌Rt△

CGB

，故

S

<

S

△.設則有由此可得不等式④.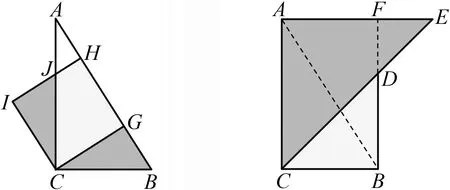

圖7 均值不等式證明之五 圖8 均值不等式證明之六

如圖8，在Rt△

ACB

的直角邊

CB

上作等腰Rt△

CBD

，過點

A

作

CB

的平行線，交

CD

的延長線于點

E

，則

S

<

S

△+

S

△，設則得不等式④.

上述證明表明，古為今用，數學史料可以幫助我們揭示均值不等式豐富的幾何內涵.

關于正弦定理，教師通常采用作高法進行證明，簡潔卻不夠直觀.我國清初數學家梅文鼎(1633—1721)在其《平三角舉要》中已運用了轉化思想證明正弦定理.實際上，翻開歷史的畫卷，正弦定理的證明豐富多彩，其基本思路是通過構造相似三角形，將角的正弦之比轉化為相似三角形對應邊的比.

證法1 如圖9，在△

ABC

中，

AC

>

AB

，延長

BA

至

E

，使得

BE

=

AC

，分別過點

A

和

E

作

BC

的垂線，垂足為

D

和

F

，于是sin

B

∶sin

C

=

EF

∶

AD

=

BE

∶

AB

=

AC

∶

AB

.

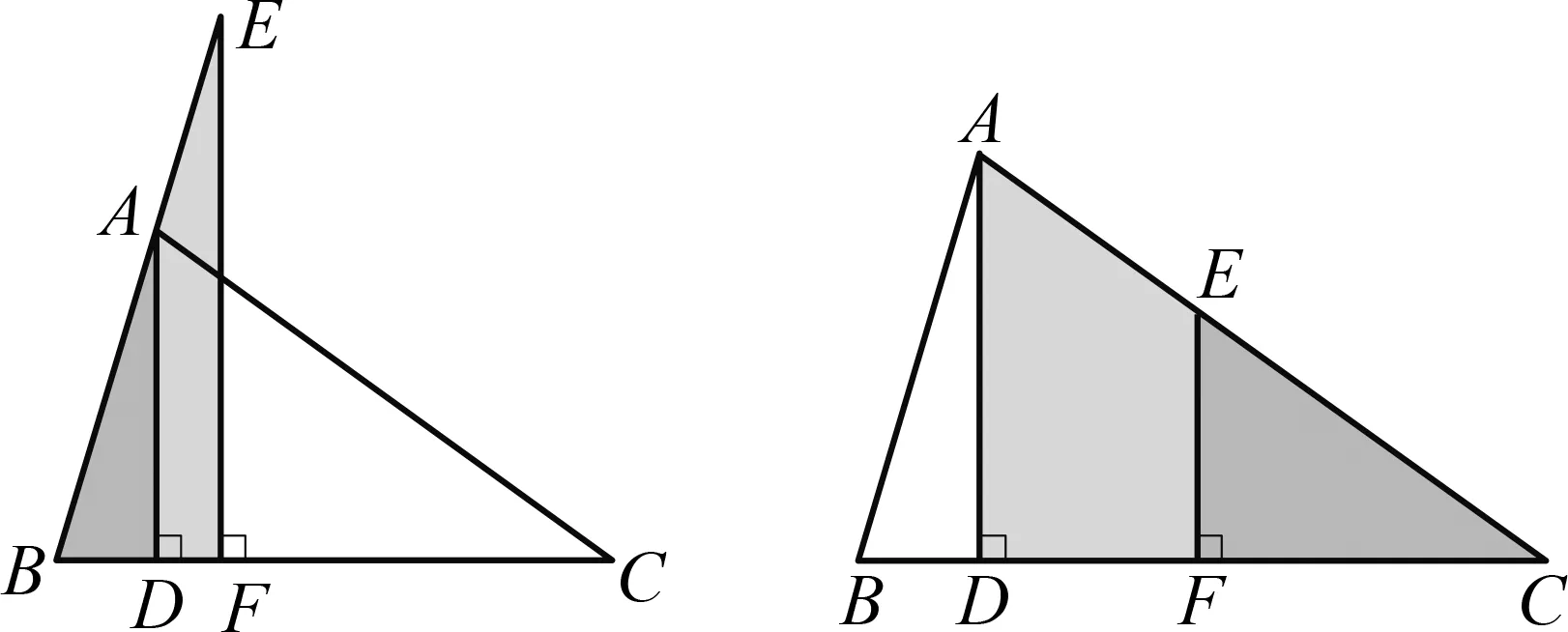
圖9 正弦定理的證明之一 圖10 正弦定理的證明之二

證法3 如圖11，在△

ABC

中，過點

B

和

C

作

AC

和

AB

的垂線，垂足分別為

D

和

E

，則sin

B

∶sin

C

=

CE

∶

BD

=

AC

∶

AB

.

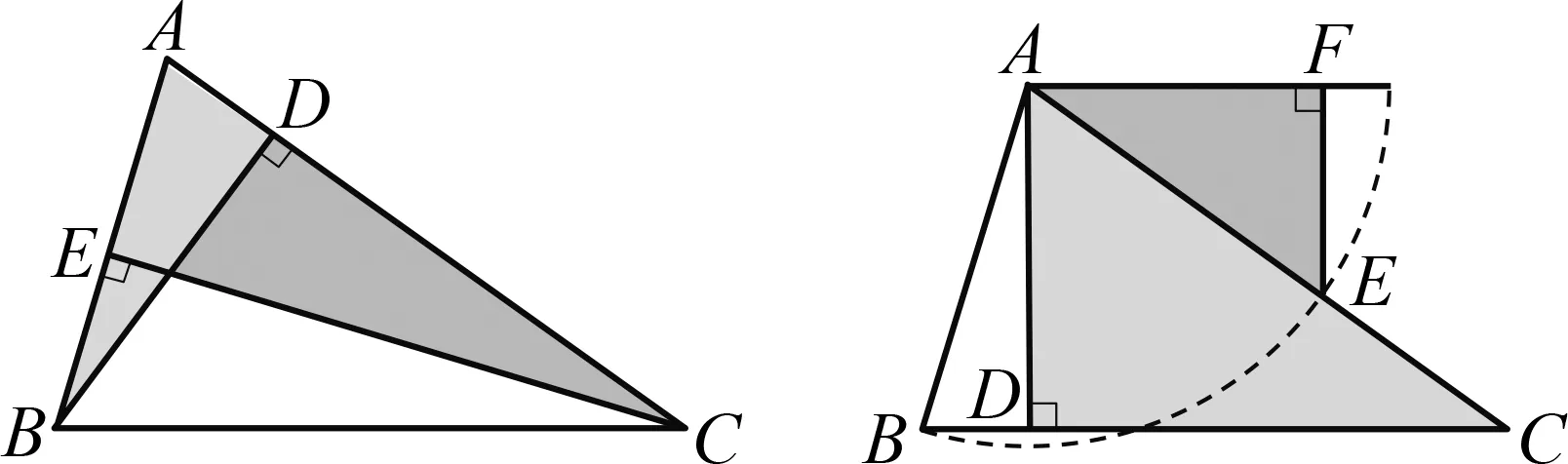
圖11 正弦定理的證明之三 圖12 正弦定理的證明之四

證法4 如圖12，在△

ABC

中，

AC

>

AB

，在

AC

上取點

E

，使得

AE

=

AB

，過點

A

作

BC

的垂線，垂足為

D

.又過點

A

作

BC

的平行線

AF

，過點

E

作

AF

的垂線，垂足為

F

，則sin

B

∶sin

C

=sin

B

∶sin∠

EAF

=

AD

∶

EF

=

AC

∶

AE

=

AC

∶

AB

.

上述證明表明，正弦定理背后蘊含著轉化的數學思想，相似三角形是溝通幾何學與三角學的一座橋梁.

3 探賾索隱

眾所周知，任何數學主題都不可能是孤立的存在，碎片化的教學不足以讓學生達到關系性理解.教學設計(特別是單元教學設計)中，教師需要揭示知識之間的聯系，而數學史可以幫助我們建立這樣的聯系，從而為學生提供探究機會，提升理解層次，落實高階思維，發展核心素養.

以圓錐曲線為例，古希臘數學家梅奈克繆斯用垂直于圓錐母線的平面截圓錐，當圓錐的頂角分別為銳角、直角和鈍角時，所截得的曲線分別稱為銳角、直角和鈍角圓錐曲線.后來，阿波羅尼奧斯用與母線具有不同位置關系的平面去截同一個圓錐，分別得到同樣的三種曲線，根據畢達哥拉斯學派的面積貼合理論，更深刻地揭示了三者之間的統一性，并據此重新對其進行了命名，這就是ellipse(橢圓)、hyperbola(雙曲線)和parabola(拋物線)的起源.在圓錐曲線單元教學中，我們可以從標準方程出發來揭示三種曲線之間的統一性.

如圖13，已知橢圓的左、右頂點分別為

A

和

B

，

P

(

x

,

y

)為橢圓上異于

A

,

B

的任意一點，

PQ

⊥

AB

，垂足為

Q

.

CD

為垂直于長軸

AB

的焦點弦(稱為橢圓的通徑)，易知過

A

作

AB

的垂線，且在垂線段上(位于

x

軸下方)取

AE

=

CD

，連結

BE

，交

PQ

的延長線于

F

，利用相似三角形性質易得

MUSIC算法是現代譜估計中的一種功率譜估計方法，基本原理是對信號Tx進行特征分解，獲取兩個相互正交的子空間，分別對應信號子空間Ts和噪聲子空間Tn，再利用其正交性構造出空間譜函數.過程可表示為

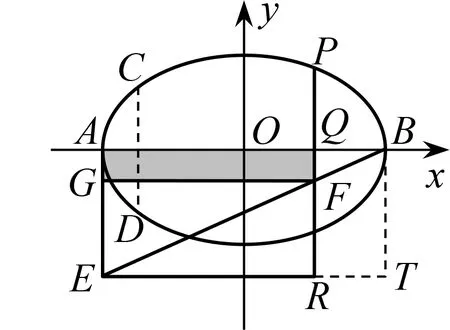
圖13 橢圓方程的幾何意義

由橢圓方程得此即

PQ

=

AQ

×

QF

.故得橢圓方程的幾何意義：矩形

AGFQ

的面積等于

PQ

.根據面積貼合理論，在長度為通徑的線段

AE

上作一個長為

AQ

、面積等于

PQ

的矩形，該矩形的寬

AG

小于

AE

，且不足于

AE

的部分矩形

GERF

與長為

AB

、寬為

AE

的矩形

AETB

相似.因矩形

AGFQ

未填滿矩形

AERQ

，故稱橢圓為虧曲線.如圖14，已知雙曲線的左、右頂點分別為

B

和

A

，

P

(

x

,

y

)為雙曲線上異于

A

,

B

的任意一點，

PQ

⊥

AB

，垂足為

Q

.

CD

為垂直于實軸

AB

的焦點弦(稱為雙曲線的通徑)，易知過

A

作

AB

的垂線，且在垂線段上(位于

x

軸下方)取

AE

=

CD

，連結

BE

并延長，交

PQ

的延長線于

F

，利用相似三角形性質易得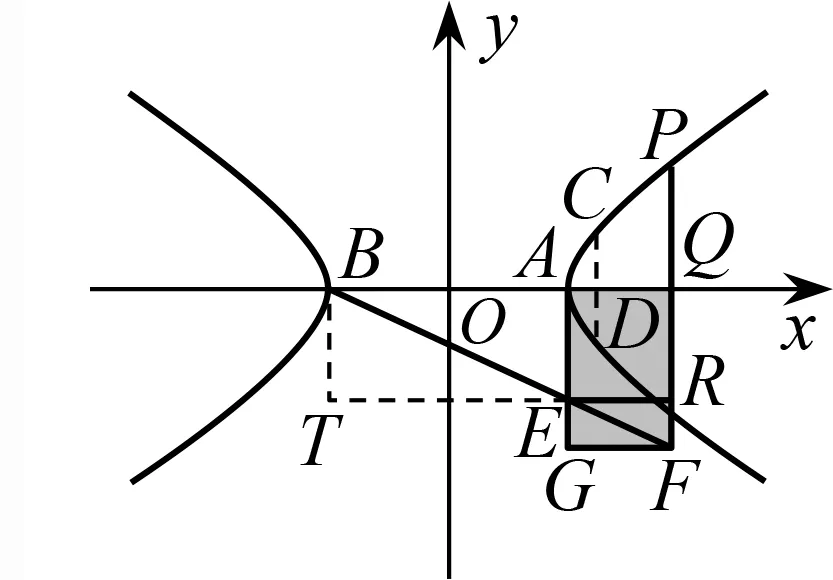

圖14 雙曲線方程的幾何意義

由雙曲線方程得此即

PQ

=

AQ

×

QF

，故得雙曲線方程的幾何意義：矩形

AGFQ

的面積等于

PQ

.根據面積貼合理論，在長度為通徑的線段

AE

上作一個長為

AQ

、面積等于

PQ

的矩形，該矩形的寬

AG

大于

AE

，且超出

AE

的部分矩形

GERF

與長為

AB

、寬為

AE

的矩形

AETB

相似.因矩形

AGFQ

超出矩形

AERQ

，故稱雙曲線為盈曲線.如圖15，已知雙曲線

y

=2

px

(

p

>0)的頂點為

A

，

P

(

x

,

y

)為拋物線上異于

A

的任意一點，過

P

向

x

軸引垂線，垂足為

Q

.

CD

為垂直于

x

軸的焦點弦(稱為拋物線的通徑)，易知

CD

=2

p

.過

A

作

x

軸的垂線，且在垂線段上(位于

x

軸下方)取

AE

=

CD

，過

E

作

x

軸的平行線，交

PQ

的延長線于

F

，

QF

=

AE

=2

p

.

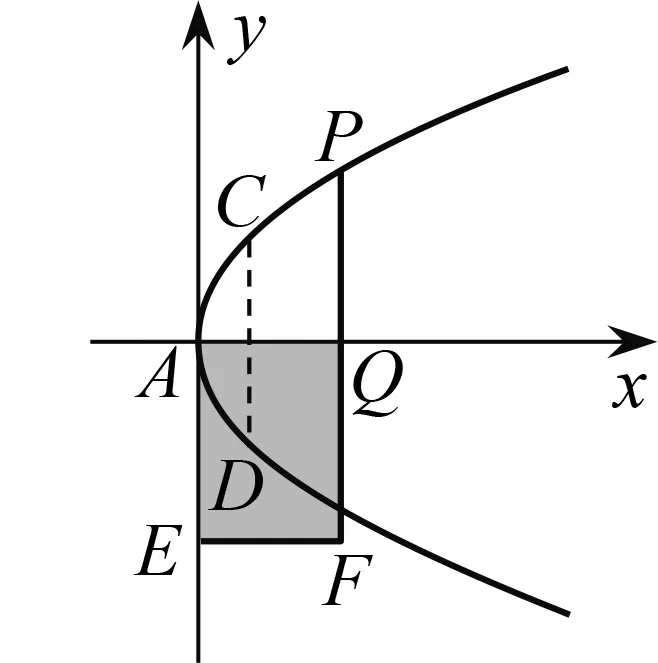
圖15 拋物線方程的幾何意義

由拋物線方程得

PQ

=

AQ

×

QF

，故得拋物線方程的幾何意義：矩形

AEFQ

的面積等于

PQ

.根據面積貼合理論，在長度為通徑的線段

AE

上作一個長為

AQ

、面積等于

PQ

的矩形，該矩形的寬恰好等于

AE

.因矩形

AEFQ

恰好占滿

AE

，故稱拋物線為齊曲線.

可見，三種圓錐曲線方程的幾何意義揭示了它們之間的統一性.

又如，今日教科書并未揭示正弦定理和余弦定理之間的密切關系，而歷史上數學家已經證明了兩者之間的等價關系.

由余弦定理，不難得到 sin

A

=1-cos

A

=,sin

B

=1-cos

B

=,sin

C

=1-cos

C

=.于是有故得正弦定理的結論.又由正弦定理得

a

sin

B

=

b

sin

A

，于是有

a

sin

B

=

b

sin

A

，即

a

=

b

+

a

cos

B

-

b

cos

A

=

b

+(

a

cos

B

+

b

cos

A

)(

a

cos

B

-

b

cos

A

)=

b

+

c

(

c

-2

b

cos

A

).同理可得另兩個等式.實際上，平面三角中的和角公式、射影公式、正弦定理和余弦定理之間有著密切的內在聯系，如圖16所示.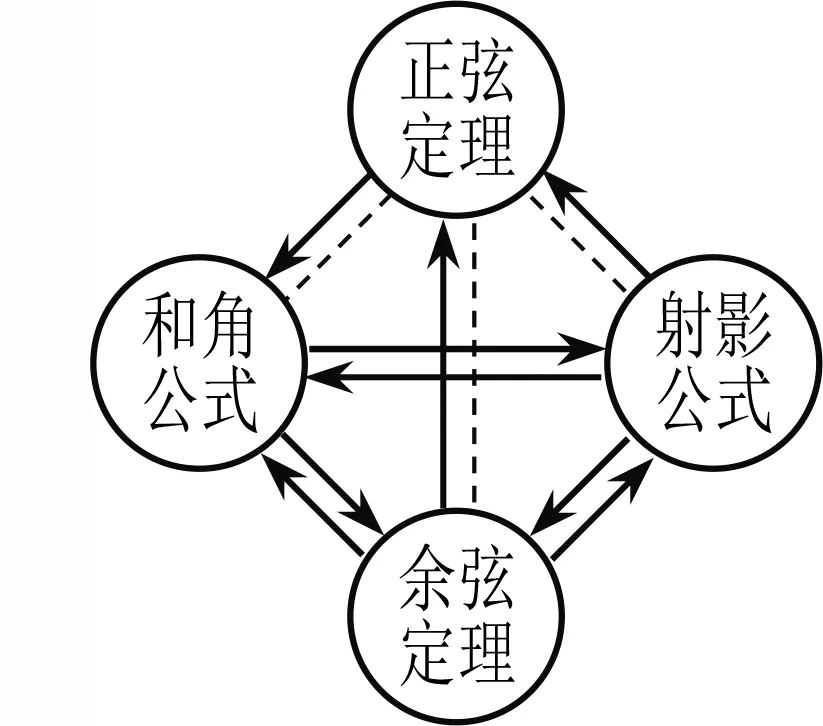

圖16 平面三角公式與定理之間的聯系

4 登高望遠

對于一個知識點的教學，不能僅僅照本宣科，作繭自縛，為知識而知識，而需轉換視角，從更高的觀點對該知識點加以審視，從而進一步構建“知識之諧”.用函數的觀點來看絕對值不等式，不難發現，它不過是函數

f

(

x

)=|

x

|的凹凸性的一種表達方式(圖17)：或即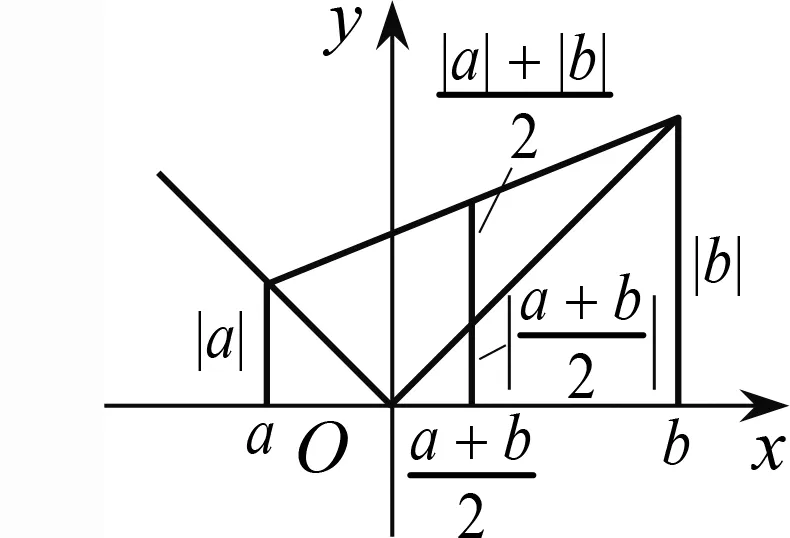

圖17 函數觀點下的絕對值不等式

類似地，若考察函數

f

(

x

)=ln

x

和

g

(

x

)=

x

的凹凸性，則分別有即得不等式人們熟悉的均值不等式鏈也可以從高觀點加以審視.可以證明，函數為單調遞增函數.又因故定義則

F

(

x

)為(-∞,+∞)上的單調遞增連續函數.由

F

(-1)≤

F

(0)≤

F

(1)≤

F

(2)可得可見，中學數學課程中出現的一些不等式，不過是有關函數性質的推論而已.

HPM課例研究的主要目的是利用數學史料來改善教學，但教學設計研討不可能僅僅局限于古代的數學史料上.事實上，在德國數學家F·克萊因(F.Klein,1849—1925)之前，函數概念并非中學數學課程的核心概念，人們很少用函數觀點來看待中學數學課程中的主題.因此，HPM研究者還需要以更寬廣的視野去研究有關主題的歷史.

5 質疑問難

正如做一道好菜既需要好的食材也需要好的烹飪技術一樣，從HPM的視角上一節好課，既需要好的數學史料也需要好的運用策略.如何將數學史料融入教學設計，特別是如何利用數學史料編制理想的數學問題，是教學研討的重要主題.

基于數學史的問題提出策略包括復制式、情境式、條件式、目標式、對稱式、串聯式和自由式七類，表1給出了不同類型的史料與問題提出策略之間的對應關系.

表1 基于數學史料的問題提出策略

類別數學史料問題提出的策略含有條件和目標公式、定理或法則復制式、條件式、目標式、對稱式、自由式數學問題復制式、情境式、條件式、目標式、對稱式、串聯式、自由式不含條件和目標概念定義自由式作圖工具自由式其他史實自由式

例如，阿波羅尼奧斯在《圓錐曲線論》中給出以下命題：如圖18，設

P

是圓、橢圓或雙曲線上一點，過

P

向對稱軸引垂線，垂足為

Q

，

T

是對稱軸上位于曲線外的一點，滿足

TB

∶

TA

=

QB

∶

QA

，則

TP

為曲線在點

P

處的切線.由該命題可得圓錐曲線切線的尺規作圖方法：如圖18，設點

P

是圓、橢圓或雙曲線上一點，

AB

為直徑、長軸或實軸，在

AB

延長線(或

AB

)上取一點

C

(

C

位于曲線外部)，使得

BQ

=

BC

，過點

B

作

AP

的平行線，交

AB

在點

C

處的垂線于點

D

，連結

DP

，交

AB

延長線或

AB

于點

T

，則

TP

即為所求的切線.事實上，根據作圖法有

TB

∶

TA

=

BD

∶

AP

=

BC

∶

AQ

=

QB

∶

QA

.據此我們可以采用自由式策略提出以下解析幾何問題：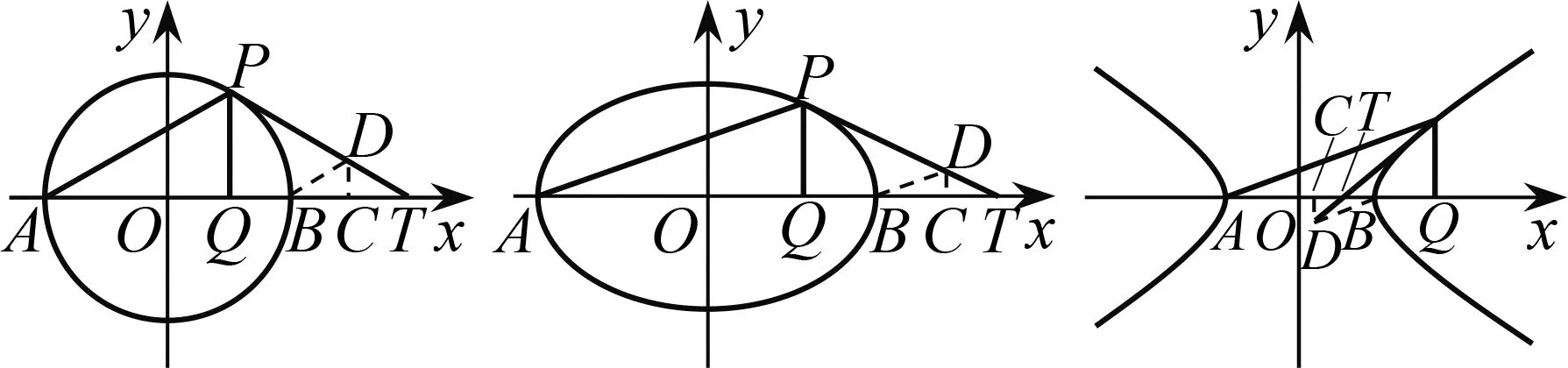

圖18 圓和圓錐曲線切線的作圖

設點

P

是圓

x

+

y

=

a

上一點，

AB

為直徑，

PQ

⊥

AB

，垂足為

Q

.在

AB

延長線上取一點

C

，使得

BQ

=

BC

，過點

B

作

AP

的平行線，交

AB

在點

C

處的垂線于點

D

.試證明：

DP

為圓在點

P

處的切線.類似地，你能給出橢圓和雙曲線的切線作圖法嗎？

數學史為數學問題的編制提供了取之不盡、用之不竭的資源.

6 歸根結底

在教學研討中發現，許多教師在運用數學史料時往往忘了“初心”，即未能深入思考為什么要采用HPM的視角、數學史究竟有什么獨特的價值、用HPM和不用HPM究竟有何不同，在實際教學中，也缺乏對整節課的提煉和升華.教學研討中，對于HPM視角下的一份教學設計，至少可從數學思想(方法之美)、核心素養(能力之助)、數學文化(文化之魅)、學科德育(德育之效)等角度加以總結.

例如，“絕對值不等式”的一種教學設計如下：從歷史上的等周問題中，抽象出等周矩形的最大面積問題，從而引出均值不等式；引導學生用代數方法和幾何方法(勾股容方模型)對不等式加以證明；再用海倫公式和均值不等式來解決古希臘的三角形等周問題：底邊固定的所有等周三角形中，面積最大的三角形具有什么形狀？這樣一份教學設計運用了三種數學思想——從特殊到一般、數形結合和化歸，落實了三種核心素養——數學抽象、邏輯推理和直觀想象，呈現了三種文化元素——知識源流、社會角色和多元文化，體現了三種德育價值——理性、信念和品質.

又如，“正弦定理”的一種教學設計如下：根據10世紀阿拉伯天文學家阿爾·庫希(al-Kuhi)測量流星的方案，提出流星測量問題，引出解三角形問題；再從《幾何原本》卷一中的“等邊對等角”“等角對等邊”“大邊對大角”“大角對大邊”四個命題出發，引出三角形邊角定量關系問題；然后引導學生從圖19所示的特殊三角形中得到特殊的邊角關系進而猜想出一般三角形的邊角關系；然后引導學生探究正弦定理的各種幾何證明；最后利用正弦定理解決流星測量問題.這份教學設計運用了一種數學思想——轉化，落實了兩種核心素養——邏輯推理和直觀想象，呈現了三種文化元素——知識源流、學科聯系和多元文化，體現了四種德育價值——理性、信念、情感和品質.

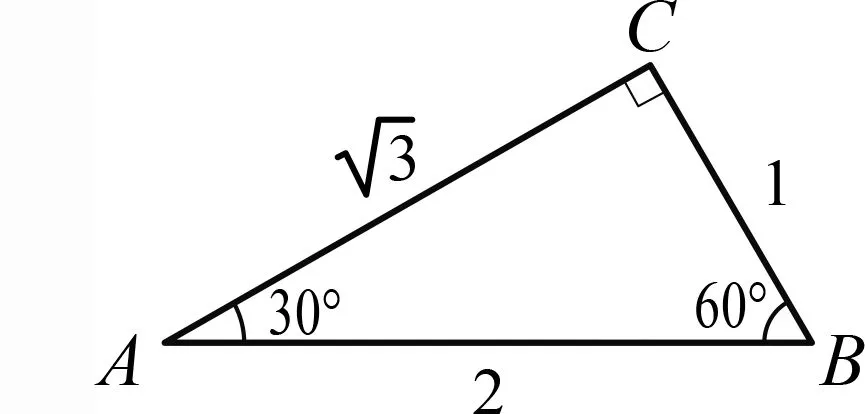
圖19 特殊直角三角形中的邊角關系

以上我們呈現了HPM視角下教學研討的一個較為完整的內容框架，其中，“追本溯源”“想方設法”“探賾索隱”和“登高望遠”解決的是“用什么數學史料”的問題，“質疑問難”解決的是“如何用數學史料”的問題，“歸根結底”解決的則是“為何用數學史料”的問題.我們有理由相信，在HPM教學理念廣泛傳播和教師在線學習研修常態化的今天，基于該框架的教學研討，對于確保HPM課例質量、促進教師專業發展、深化HPM實踐研究必將產生積極的影響.