BCC 點陣結構力學性能與應用
張璠, 田國富
2001 年, 美國哈佛大學的Hutchinson 教授首次[1]提出點陣結構的概念, 是由桿件在空間上的結點與結點間的連接組成, 按一定規則重復排列,也常被視作微桁架結構。
隨著3D 打印技術的成熟, 點陣結構制備的復雜程度和成本大大降低。 同時, 由于點陣結構具有輕質、 減震、 吸能和傳熱滲透等功能特性[2],在航空航天、 機械、 醫療、 汽車等行業應用廣泛[3~5]。
本文研究點陣結構中最為經典的BCC 點陣結構, 分析其力學性能, 并應用在輕量化設計中,證明點陣結構在輕量化設計中有明顯優勢。
1 BCC 點陣結構模型與參數
1.1 BCC 點陣單胞的結構
BCC 點陣結構模型中的每個單胞模型由8 根橫截面為圓形的桿件組成, 各桿件在中心點相交且長度相同, 每根桿件長度為l, 單胞底邊為正方形, 底邊長為l1, 單胞的側邊長為l2, 桿件的半徑為r, 直徑為d, 桿件與底面夾角為θ( 見圖1、 圖2)。
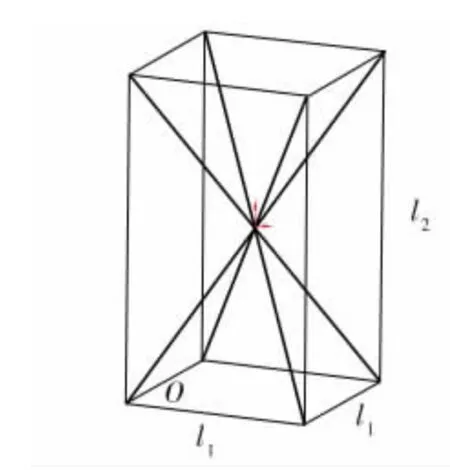
圖1 BCC 點陣結構單胞模型示意圖

圖2 BCC 點陣結構
1.2 BCC 點陣結構的相對密度
相對密度用來描述材料的輕質化程度, 也是影響點陣結構力學性能的關鍵因素之一。 由于點陣結構的結構特殊性, 以及整體結構是由點陣單胞在空間上呈周期性排列分布組成的, 整體結構的相對密度可由單胞的相對密度得到, 所以取單胞的相對密度進行分析。
根據點陣結構的幾何參數可得到桿長為:

同時, 根據相對密度的定義可以得到BCC 點陣結構單胞的相對密度為:

2 BCC 點陣結構的等效彈性模量
彈性模量是工程材料重要的性能參數, 負責衡量物體抵抗變形能力, 也是研究材料力學性能的重要指標。 因此, 將點陣結構視為一種材料并研究其等效彈性模量對研究其力學性能十分重要。
為了研究靜態力學性能, 參考文獻[6] 引入以下假設:
(1) 對制備點陣結構的材料要求連續性、 各向同一性及均勻性。
(2) 組成點陣結構的桿件橫截面為圓形。
(3) 點陣結構單胞中所有桿件都屬于細長桿。
(4) 當有外部載荷作用時, 各桿件只發生微小變形。
當點陣結構在豎直方向上受到載荷時, 每個桿件承受的壓力為Pr, 四個桿件的均分壓力載荷為P(見圖3), P=4Pr。

圖3 BCC 桿件受力示意圖
取其中一個單一胞體中的桿件進行靜力學分析, 由于點陣結構具有對稱性, 故對點陣結構受力模型進行簡化, Pr從頂端點移至B 點產生的彎矩為:


根據得到的結果可知, 點陣結構的等效彈性模量與桿件的半徑成正比, 與桿件長度成反比, 即桿件半徑越大, 桿件長度越小, 點陣結構的承載能力越強。
3 在輕量化設計中的應用
筆者以典型連桿結構為例, 運用點陣結構對其進行輕量化設計。 根據連桿的工作特點, 對底部的螺栓孔做固定約束, 在頂部圓環內中心設置遠程力, X 和Z 方向各100 N。
按照以上載荷邊界條件分析(見圖4)。

圖4 連桿機構有限元分析結果
通過應力分布可以看出, 整體結構最大應力集中在連桿與底部圓環的連接側, 由于載荷條件的特殊性, 可知整體結構最危險的地方就是連桿與頂部圓環、 底部圓環的連接部分, 此外, 連桿中間部分的應力非常小, 應力集中在外側, 故從輕量化角度考慮, 填充部分選擇在連桿中間位置以實現輕量化設計(見圖5)。

圖5 連桿-點陣結構填充效果圖
填充后的模型轉邊界條件與載荷條件保持不變, 再次分析得到填充后的結果( 見圖6~7, 表1)。

表1 連桿結構填充前后有限元分析結果

圖6 連桿-點陣結構有限元分析結果
結果表明, 填充前后連桿的質量及體積均發生較大改變, 填充后重量下降41.67%, 體積下降41.34%; 連桿整體結構的應力分布發生改變, 填充前, 連桿中間部分的應力很小, 填充后整體結構的最大應力值變大, 出現在填充部位的點陣結構上。 由應力分布云圖可知, 填充改變了填充部分的應力分布, 而其他部分應力分布的改變非常小。 對比發現, 點陣結構的填充不僅改善整體結構的應力分布, 且大大減輕了整體結構的重量和體積, 證明點陣結構在輕量化設計上的優勢, 同樣表明點陣結構對連桿結構輕量化設計的有效性。 定義相對剛度[7]為最大位移量與模型體積的比值, 通過計算得出填充后模型的比剛度是填充前的2.66 倍,故應用點陣結構同時實現輕質與提升連桿結構剛度的功能。

圖7 連桿結構填充前后位移分布云圖
4 結 語
隨著增材制造技術不斷發展, 點陣結構的制備更加方便, 成本大大降低, 點陣結構的應用更加廣泛。 現在, 全球對點陣結構性能及應用的發掘仍在繼續, 包括點陣結構快速建模軟件、 點陣結構力學性能分析方法的開發, 對點陣結構特性的探索及點陣結構快速填充技術的實現等。

