升力式飛行器助推段多約束彈道優化設計

梁欣欣,王 惠,姜 威

(北京宇航系統工程研究所,北京 100076)

升力式飛行器一般在某一高度處入軌,通常采用多級固體運載器經助推段飛行將其助推至入軌點。由于整個助推段全部在復雜大氣環境中飛行,彈道設計約束條件較多。助推段彈道設計除了要滿足入軌條件外,還需提供盡可能大的入軌速度。目前,對于升力式飛行器的軌跡優化問題較多,多偏重于優化算法與優化方法研究,過程較為復雜、效率不高,工程應用可操作性不高。本文旨在基于工程設計方法,研究助推段軌跡優化的設計方法。

本文以三級固體運載器為研究對象,提出了升力式飛行器助推段彈道設計方法,建立了多約束下以入軌速度最大為目標的優化模型,并以牛頓迭代法確定初值,且以序列二次規劃(sequential quadratic programming,SQP)法進行優化仿真。仿真獲得了滿足多約束條件下的優化解,驗證了升力式飛行器助推段彈道設計方法的正確性和有效性。

1 助推段彈道設計方法

升力式飛行器助推段彈道具有飛行高度低、轉彎角度大的特點,需要在入軌點處完成三級固體運載器從垂直向水平的轉彎過程。三級固體運載器二級發動機為兩擋變推力發動機,各級發動機均為耗盡關機方式,助推段一直在大氣中飛行,飛行環境復雜,因此助推段彈道設計需盡可能提供較好的飛行環境。根據各級飛行特點,進行助推段俯仰程序角設計,設計結果如圖1所示。圖中,,,分別對應各級攻角轉彎時的最大負攻角;(=0,1,…,8)為各階段時刻點,為二級飛行兩檔推力間的無動力滑行時間,為二三級分離后無動力滑行時間;,,分別為對應定軸飛行的俯仰程序角。

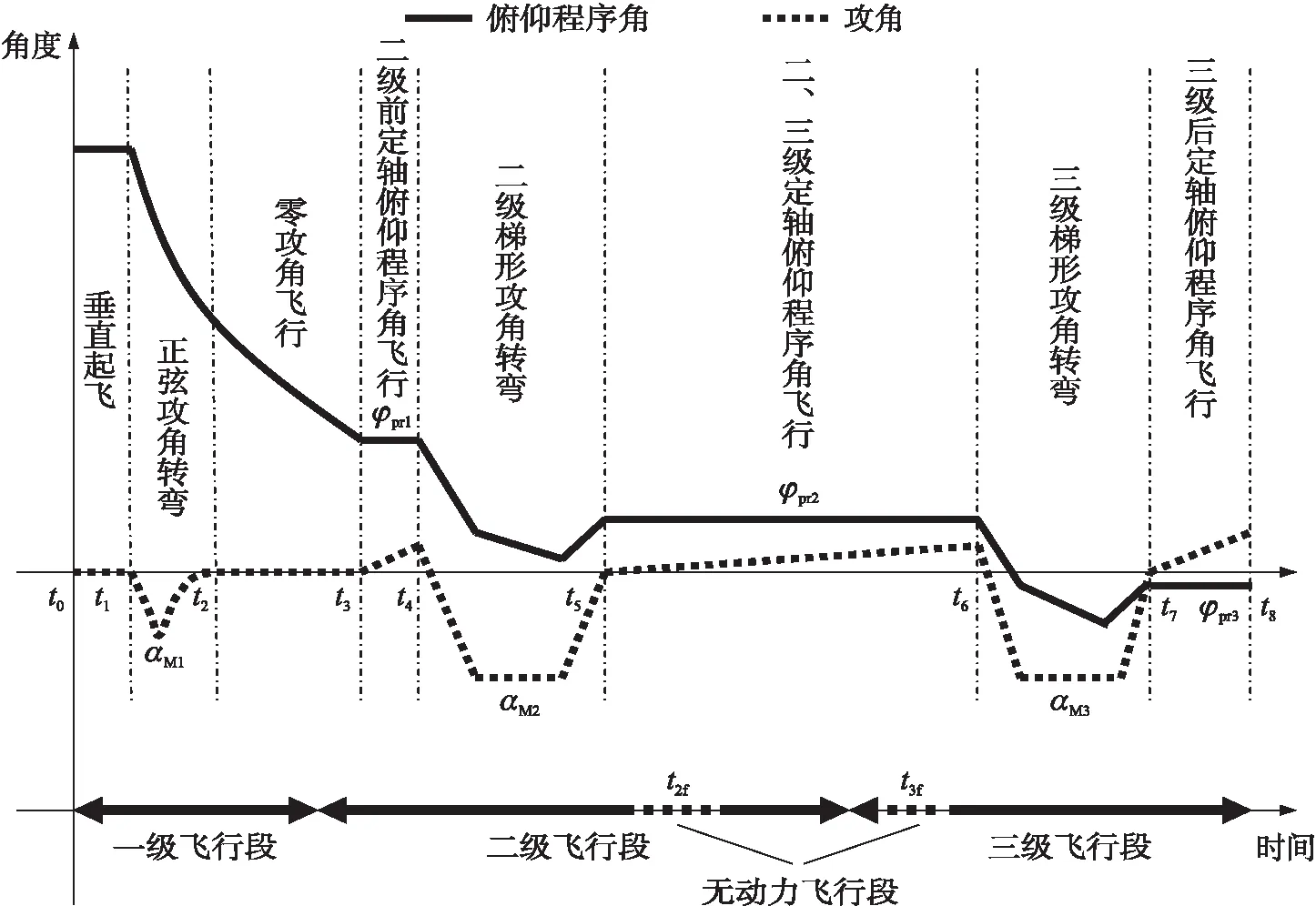
圖1 飛行程序角設計示意圖

圖1中各段俯仰飛行程序角表達式為

(1)

式中:為速度傾角;為俯仰程序角;(),(),()分別為一級、二級、三級攻角轉彎段攻角隨時間變化的函數。

固體運載器的程序角設計方法如下:

①垂直起飛段。三級固體運載器為垂直發射,在進入攻角轉彎時,需要一段時間進行垂直飛行。

②正弦攻角轉彎段。三級固體運載器在一級發動機額定工作段開始攻角轉彎,這一時間不能太早,保證發動機工作在額定狀態下,轉彎具有足夠的控制力;同時,這一時間不能太晚,否則轉彎具有較大阻力,損失運載器能量。一級要穿越稠密大氣,故需要在亞音速階段完成攻角轉彎。此段采用正弦函數攻角構造法進行轉彎。

③零攻角飛行段。在一級跨音速及二級飛行段初始段,飛行高度低,大氣稠密,為減小大氣阻力,運載器以零攻角飛行,飛行結束時刻點可根據飛行至某一高度確定。

④二級前定軸俯仰程序角段。在二級飛行段高度較高時,可實行定軸俯仰程序角飛行,對于拋頭罩等分離時序的實現具有積極意義。

⑤二級梯形攻角轉彎段。在二級以梯形攻角形式進行轉彎,減小運載器飛行的當地彈道傾角。由于轉彎時機早,二級相對于三級轉彎效率高,但同時將消耗較多能量。

⑥二級、三級定軸俯仰程序角段。在二級攻角轉彎后、三級攻角轉彎前,均實行定軸俯仰程序角飛行,其中包含三級發動機點火前的無動力飛行段。采用定軸飛行形式對于二三級分離具有積極意義。

⑦三級梯形攻角轉彎段。在三級以梯形攻角形式進行轉彎,進一步減小運載器飛行程序角,由于此時大氣稀薄,可采用較大攻角轉彎飛行。

⑧三級后定軸飛行段。在轉彎結束后,以某一定值俯仰程序角助推運載器入軌。

2 優化模型與求解流程

對助推段飛行特點分析和飛行程序角設計后,本節建立了升力式飛行器助推段優化模型,并進行了優化流程設計。

2.1 目標函數

選取初始入軌速度最大為優化目標。定義目標函數()=-,尋找優化設計變量,使得目標函數()最小,即:

min()=-

(2)

2.2 優化變量

在進行飛行程序角設計時,各級攻角轉彎最大負攻角,,作為主要的設計變量,因此可作為優化變量;,,,分別為二三級攻角轉彎段起始時刻和終止時刻,其需選擇在發動機額定工作時間段內,并具有一定的可調節空間,可作為優化變量;此外,兩段無動力飛行的飛行時間,可作為優化變量。因此,選取,,,,,,,,作為優化變量,即:

=()

(3)

2.3 約束條件

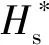
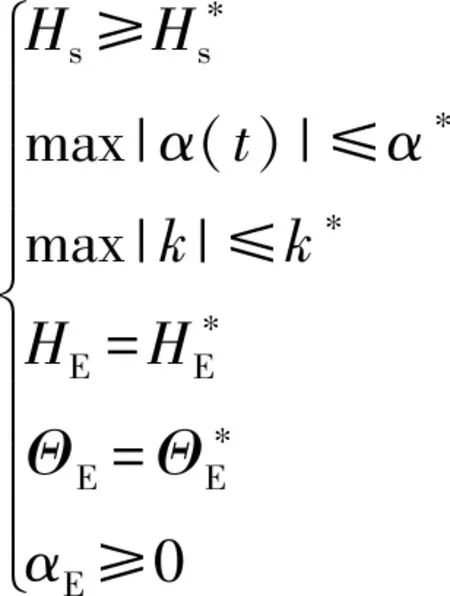
(4)

式中:為一二級分離高度,為俯仰程序角變化率,為入軌點高度,為入軌點當地彈道傾角,為入軌點攻角。

2.4 優化模型

綜合以上各式,得到升力式飛行器助推段彈道優化模型如下。

目標函數:

min()=-

優化變量:

=()

約束條件:

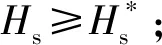
②攻角限幅約束max|()|≤;

③程序角斜率約束max||≤;

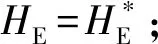
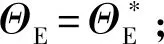
⑥入軌點攻角約束≥0。

2.5 優化流程

以牛頓迭代算法選取優化初值,并利用SQP法進行優化求解。由于自變量和約束較多,采用多輪次多維度牛頓迭代,為優化提供較為準確的初值,提高優化效率。通過深入分析模型各優化變量與約束條件的耦合關系,找出設計變量對約束的靈敏度影響,以一維或二維牛頓迭代快速找出滿足部分約束的設計變量參數,從而達到降低優化設計變量維度、減少約束條件、提升優化效率的目的,優化流程如圖2所示。

圖2 優化流程圖

3 仿真結果

針對前文給出的升力式飛行器助推段彈道設計方法、優化模型與優化流程,開展優化仿真。優化變量上下限、初值、牛頓迭代初值、優化解如表1所示,相關約束條件設定值、計算值和滿足情況如表2所示。

從表1和表2中可以看出,約束條件均得到滿足,優化變量值均在設計變量的優化范圍內。此外,優化得到的入軌速度高出原來的3.1%,優化結果理想,進而證明了升力式飛行器助推段彈道設計方法的正確性,也驗證了優化求解流程的有效性。優化后的彈道仿真結果無量綱化曲線如圖3～圖6所示。

表1 優化變量值

表2 約束條件設定值

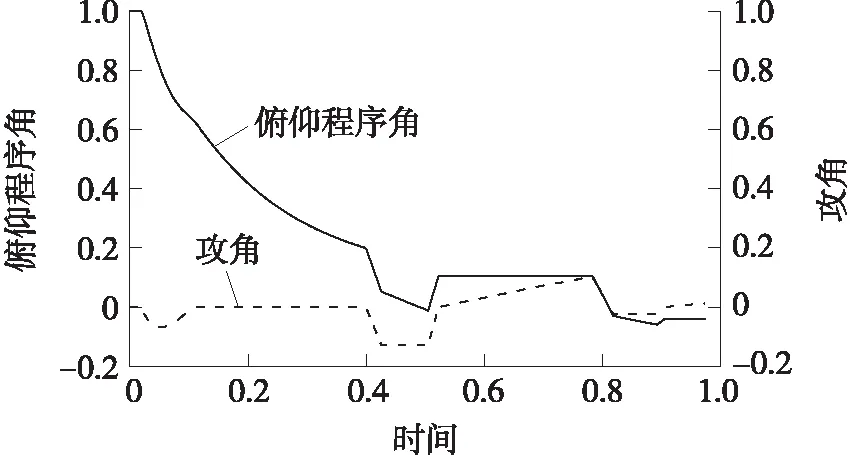
圖3 攻角-時間和俯仰程序角-時間無量綱曲線

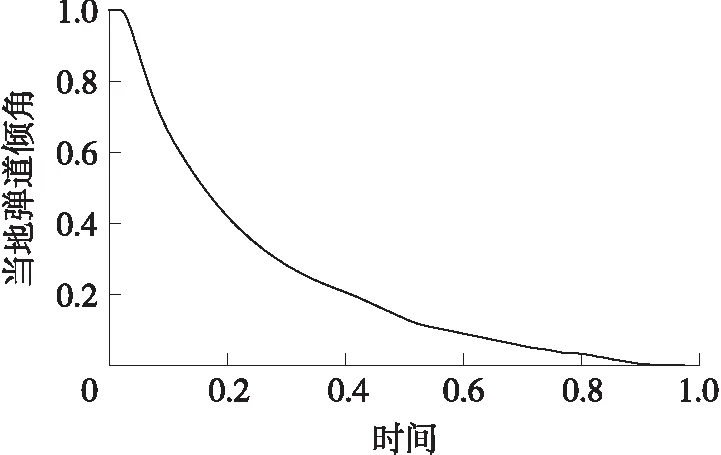
圖4 當地彈道傾角-時間無量綱曲線

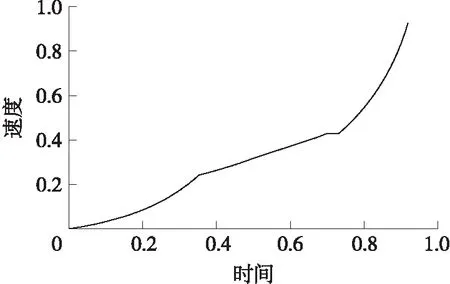
圖5 速度-時間無量綱曲線

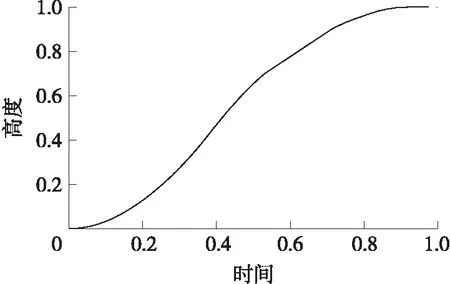
圖6 高度-時間無量綱曲線

4 結束語

本文首先給出了升力式飛行器助推段彈道設計方法,選擇了優化變量,確定了飛行過程約束和入軌點入軌約束,以入軌速度最大為優化目標,建立了優化模型,并以牛頓迭代法確定優化初值,且以序列二次規劃法開展優化仿真。從優化結果來看,約束條件均得到滿足,優化得到的入軌速度提高了3.1%,優化結果理想。本文中升力式飛行器助推段彈道設計方法具有較強的工程適用性,優化模型建立方法與優化求解流程可為其他優化問題提供參考。