基于FPCA與DEELM的彈藥協調機械臂性能故障診斷

閆少軍,文 浩

(1.內蒙古第一機械集團有限公司,內蒙古 包頭 014000;2.南京理工大學 機械工程學院,江蘇 南京 210094)

彈藥協調器是大口徑火炮彈藥自動裝填系統的重要部件,負責從彈倉和藥倉中接受彈丸和模塊藥并傳輸至炮尾后部推彈線上。彈藥自動裝填系統是一個存在沖擊載荷且工作環境惡劣的復雜機電液一體化系統,在使用中存在諸多故障,例如協調器液壓系統故障引起定位精度超差,嚴重影響火炮武器系統的可靠性。如何從系統狀態信息中提取表達系統狀態的量化的故障特征,是實現彈藥自動裝填系統智能故障診斷的關鍵之一。

傳感器檢測得到的系統狀態信息不能直接使用,需要進行特征提取,將信號中的故障特征信息和與故障無關的特征信息分離,同時起到降維的作用。在彈藥自動裝填系統的故障診斷研究中,特征提取方法主要采用經典信號處理方法和多元統計分析方法。機電系統中的大多數物理量隨時間的變化曲線都是連續且具有一定平滑性的,通常以離散點集形式表示,傳統的信號處理方法忽略了數據本身的平滑特性。函數型數據分析(functional data analysis,FDA)將觀測數據表示為平滑的曲線或連續的函數,實現有限維數據到無限維數據的轉換,得到的數據信息更豐富、可靠,目前FDA已廣泛應用于工業生產監督和金融領域等。在故障診斷領域中,FPCA用于提取故障特征,文獻[7]使用FDA建立了彈藥協調器故障因素與故障特征之間的對應關系,通過BP神經網絡進行診斷,但由于無法對真實的裝備破壞以獲取故障樣本,只是利用仿真樣本對診斷方法的可行性進行了驗證。

本文針對某彈藥協調機械臂定位精度超差性能故障,基于FPCA對協調過程中的支臂角位移曲線進行特征提取,并對提取的特征進行分析與選擇,將選擇的特征參數作為故障特征集,通過DEELM實現故障診斷,使用仿真數據與模擬故障實驗數據驗證了該方法的可行性。

1 協調機械臂動力學建模

圖1為某彈藥協調器的原理實驗臺架,支臂由MAXON直流電機通過2個行星齒輪減速器驅動,負載安裝在支臂自由端;氣彈簧連接到支臂上,用于平衡支臂和負載的重力矩,減小驅動電機的負載;采用PC作為上位機,編碼器提供支臂的角位移和角速度信號。

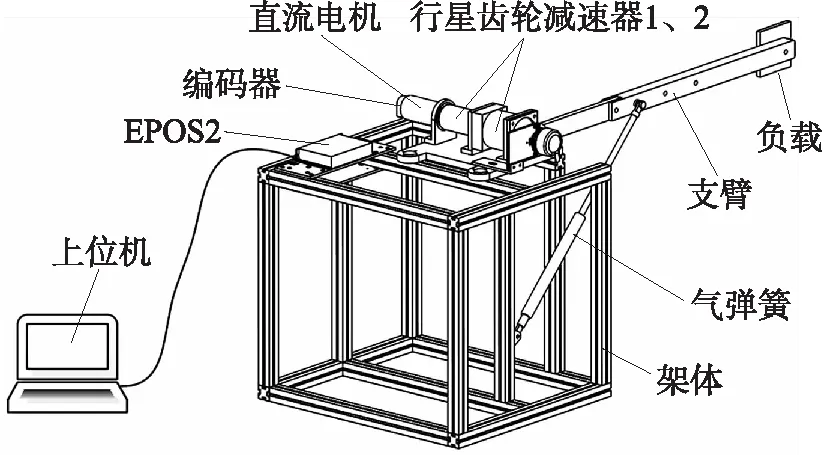
圖1 協調機械臂實驗臺架

真實的系統不便于對故障因素進行人為設定,為了便于獲取故障樣本數據,建立協調機械臂的動力學模型,以支臂為系統的等效構件,其動力學方程為

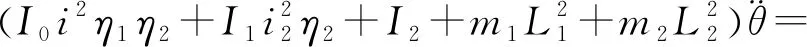
(1)

式中:為支臂的角位移;為電機轉子的轉動慣量;,分別為行星齒輪減速器1和行星齒輪減速器2的轉動慣量;為系統總的傳動比,=;和分別為行星齒輪減速器1和行星齒輪減速器2的傳動比;和為行星齒輪減速器1和行星齒輪減速器2的傳動效率;為支臂的質量;為負載的質量;為支臂質心至支臂轉軸中心的距離;為負載質心至支臂轉軸中心的距離;為直流電機的輸出轉矩;為氣彈簧對支臂提供的平衡力矩;為支臂與負載的重力矩,為支臂轉軸處的摩擦力矩。氣彈簧活塞桿和外筒的質量較小且運動速度相對緩慢,在計算時忽略了氣彈簧的動能。

采用比例-微分控制,驅動電機的輸出力矩為

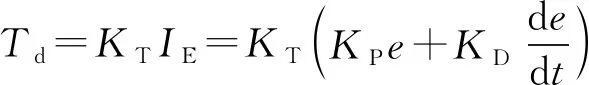
(2)

式中:為電機轉矩常數,為電機期望電流,為編碼器測量的角位移與目標角位移之間的偏差,=20-,為編碼器輸出信號與真實信號的比值,為支臂真實角位移;為比例放大系數;為微分常數。

平衡力矩取決于支臂轉角和氣彈簧氣體壓力:

(3)

式中:為氣彈簧提供的平衡力方向與支臂轉軸中心的距離,為氣彈簧內部氣體初始壓力,為氣彈簧活塞面積,為氣體初始體積,Δ為活塞行程,為氣體多變指數,在特定的熱力學過程中可以認為是定值。和Δ都與支臂角位移有關。

支臂和負載的重力矩取決于支臂的角位移:

=cos(+)+cos(+)

(4)

式中:為初始位置支臂質心與支臂轉軸中心連線和水平線之間的夾角。

支臂轉軸處的摩擦力矩通過LuGre摩擦模型來描述,LuGre模型能夠較準確地描述摩擦過程中的黏滑運動、摩擦滯后、預滑動位移和變最大靜摩擦力等特性,它假設接觸面通過彈性鬃毛接觸,鬃毛的平均偏移量用表示,鬃毛的彎曲產生了摩擦力矩,模型表示為

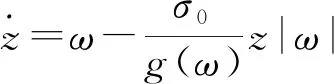
(5)

()=+(-)e-||

(6)

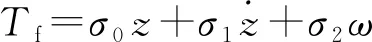
(7)

式中:為支臂角速度,為鬃毛的剛度,為微觀阻尼系數,為黏性摩擦系數,()描述了Stribeck效應,為庫倫摩擦力矩,為靜摩擦力矩,為Stribeck特征速度,為形狀校正系數。摩擦模型參數中,和屬于動力摩擦因數,、、、和屬于靜力摩擦因數。

根據式(1)～式(7)可對協調機械臂的協調過程進行求解。協調機械臂的動力學解析模型中有些參數是未知且難以測量的,如氣彈簧的初始壓力,氣體多變指數以及LuGre摩擦模型中的靜力摩擦和動力摩擦因數,這些參數通過辨識的方法獲取,參數辨識過程在這里不展開敘述。

以20°為協調目標角度,進行了3次協調過程的測試,最終支臂角位移分別為19.73°,19.66°和19.63°;同時,利用協調機械臂解析模型進行相同狀態下的仿真,最終支臂角位移為19.54°。仿真結果與測試結果對比如圖2所示。由圖2可知多次協調過程的一致性較好,并且解析模型的輸出與測試結果較為吻合,表明協調機械臂的解析模型能夠較好地反應真實系統的特性。

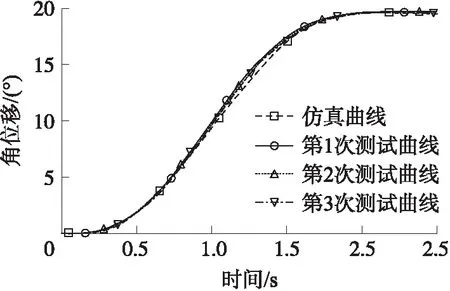
圖2 仿真結果與測試結果對比

2 抽樣仿真與模擬故障實驗

協調機械臂的協調過程為在2.5 s內向下轉動20°,并且要求定位精度不超過±0.6°,其性能故障表現為定位精度超差。根據實際彈藥協調器的調研情況,結合協調機械臂實驗臺架的結構特點分析,選取造成定位精度超差的原因為氣彈簧初始壓力變化和支臂角位移測量誤差,即和偏離正常值范圍。分別改變動力學解析模型中和的值進行協調過程仿真,得到的臨界取值范圍為1.02～1.57 MPa,的臨界取值范圍為[0.955,1.0]。考慮到2種因素同時偏離正常取值范圍的情況,定義表1所示的故障類型與代號。

表1 故障類型代號

分別在表1所示的6種故障類型對應的和取值范圍內進行拉丁超立方抽樣,然后將其代入動力學解析模型中,仿真得到支臂角位移曲線,每種情況抽樣仿真30組,共得到180組樣本。

利用協調機械臂實驗臺架進行模擬故障實驗。在保持初始位置氣彈簧與支臂夾角不變的情況下,通過改變氣彈簧的長度來模擬氣彈簧初始壓力變化;在LabView程序中將編碼器反饋的角位移信號乘以系數模擬編碼器測量誤差,表1所示的每種故障類型進行2組模擬故障實驗,得到12組實驗樣本曲線。

將上述仿真得到的曲線,每種情況隨機選擇25組作為故障診斷模型的訓練樣本,共150組;每種情況剩余的5組仿真樣本與模擬故障實驗的12組實驗樣本共同作為測試樣本,共42組。

3 基于FDA和FPCA的曲線特征提取

3.1 數據函數化與平滑處理

在對協調器支臂角位移曲線進行FPCA特征提取時,首先通過B樣條基函數將樣本數據函數化,利用粗糙懲罰函數對函數化后的樣本數據進行平滑處理。

假設第(=1,2,…,)個觀測樣本包含一系列離散的觀測數值1,2,…,,對應的采樣時刻為1,2,…,,其函數形式()由個已知相互獨立的基函數()的線性組合表示:

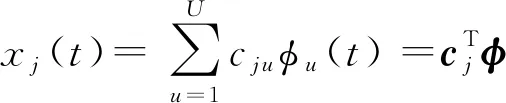
(8)

式中:=(()()…())為個基函數()組成的函數型向量,=(12…)為相應的基函數系數向量。

對于非周期性數據通常采用B樣條基函數展開,B樣條函數根據以下方程組進行遞歸求解:

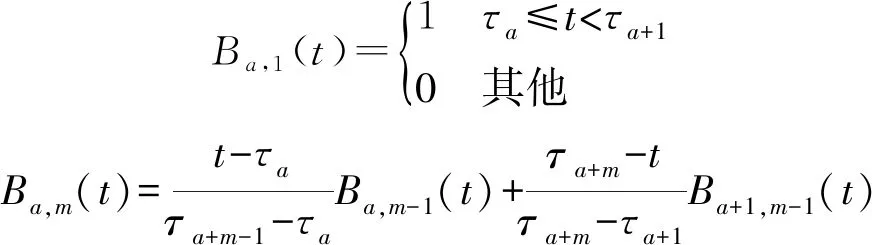
式中:(=1,2,…,)為區間[1,]上的等間距節點,為B樣條基函數的階數,且>1。

估計系數向量最簡單的方法是利用最小二乘準則最小化誤差平方和,求解時基函數()的個數越大,估計值的偏差越小,方差越大,平滑性越差,為控制平滑程度,引入二階粗糙度懲罰():

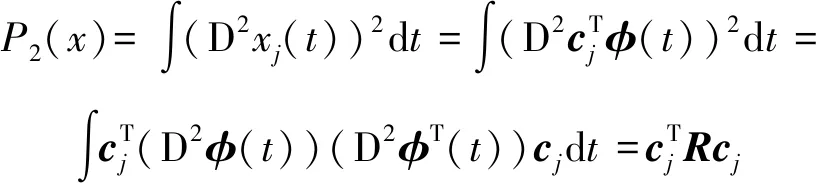
(9)

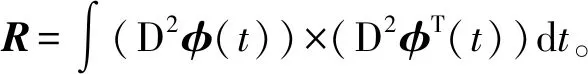
令為加權矩陣,為平滑參數,使用加權最小二乘法最小化誤差平方和估計系數向量:

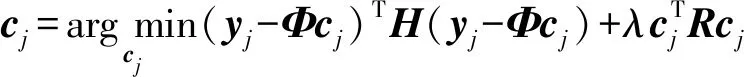
(10)

式中:為觀測樣本的向量形式,為基函數離散值組成的×階矩陣。

基函數系數向量的估計值為

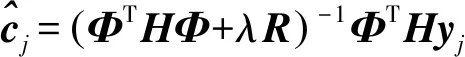
(11)

3.2 函數型主成分分析方法

主成分分析法是一種經典多元統計分析方法,也是一種常用的降維方法,FPCA是主成分分析到Hilbert空間的推廣,其主成分是特征函數。根據RAMSAY等的推導,特征函數()滿足以下方程:

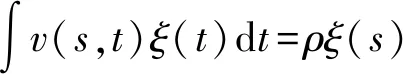
(12)

V=

(13)

主成分函數同樣需要平滑處理,考慮最大化帶有粗糙度懲罰的樣本方差:

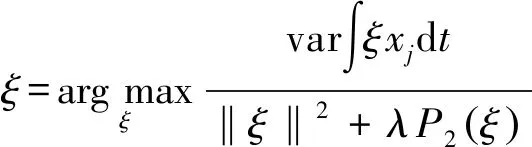
(14)

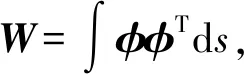
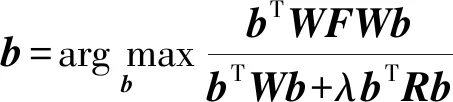
(15)

對應的廣義特征值問題:

=(+λ)

(16)

進行Cholesky分解+λ=,定義=,式(16)轉化為

()()=()

(17)

定義=,式(17)可寫為

()=ρ

(18)

這是標準的特征值問題,可依次求解出、和特征函數。類似于傳統的主成分分析,按照上述過程可以得到前階主成分函數。將去均值后的樣本函數與各個特征函數作內積:

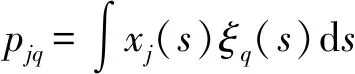
(19)

式中:()為第(=1,2,…,)階主成分函數。

所得結果作為函數型主成分得分(functional principal component score,FPCS),即FPCA提取的曲線特征參數。

3.3 樣本曲線特征提取

首先將仿真樣本數據和實驗樣本數據函數化,使用圖3所示的4階B樣條基函數進行函數展開,同時使用平滑參數為100的2階粗糙懲罰函數進行數據平滑,圖4為函數化后的樣本數據。

圖3 B樣條基函數系統

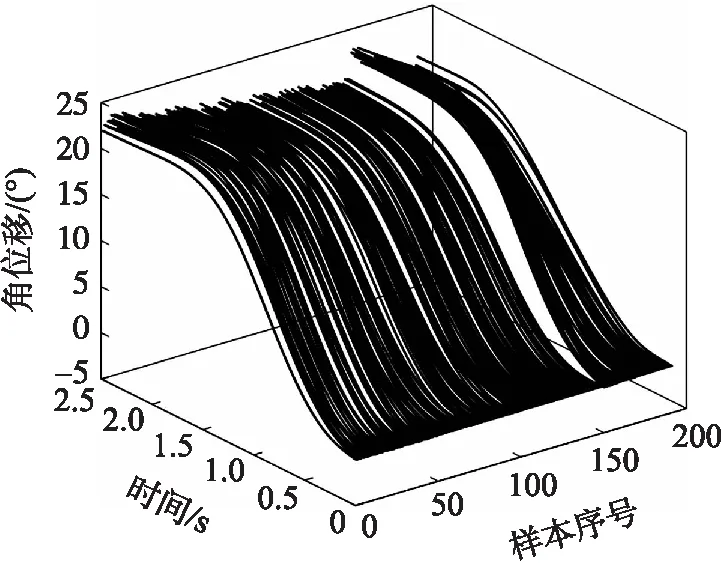
圖4 函數化后的角位移曲線

樣本數據函數化后去均值,采用與函數化過程同樣的粗糙度懲罰函數和平滑參數計算前10階主成分函數,并計算前10階主成分函數的占比,即按式(18)計算得到的各特征值占其總和的比率,前3階主成分函數占比為0.980 2,0.016 3和0.003 0,累計占比為0.999 5,第4到第10階主成分函數占比很小,因此保留了前3階主成分函數,如圖5所示。

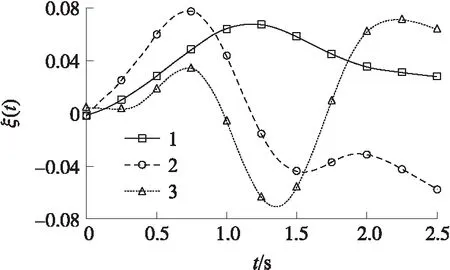
圖5 角位移曲線前3階主成分函數

對函數化后的樣本曲線與前3階主成分函數進行內積計算得到FPCS。圖6為150組訓練樣本數據的前3階FPCS,第1階和第2階FPCS能夠較好地體現曲線特征對不同系統狀態的反映,因此選取前2階FPCS作為支臂角位移曲線的特征參數,并將其作為ELM的輸入參數。提取的特征參數對不同故障類型的分類效果如圖7所示。

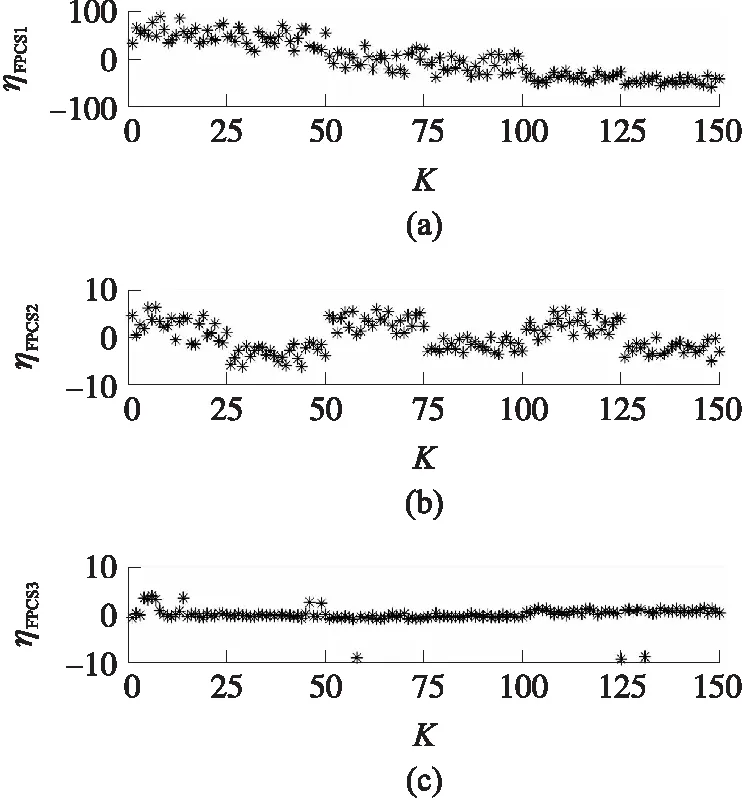
圖6 訓練樣本數據前3階FPCS

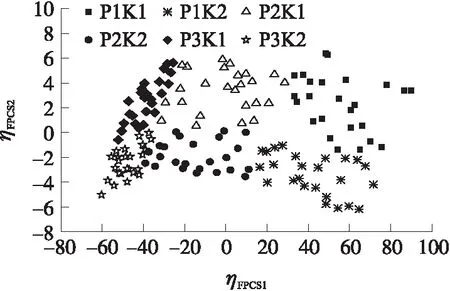
圖7 前2階主成分得分的分類效果

4 基于DEELM的故障診斷

4.1 基于DEELM的故障診斷模型

極限學習機(extreme learning machine,ELM)是一種基于單隱層前饋神經網絡的機器學習算法,廣泛應用于分類和回歸問題。分類問題的ELM網絡如圖8所示,輸入層為對應特征參數的個節點,隱含層有個節點,輸出層節點為對應的分類。

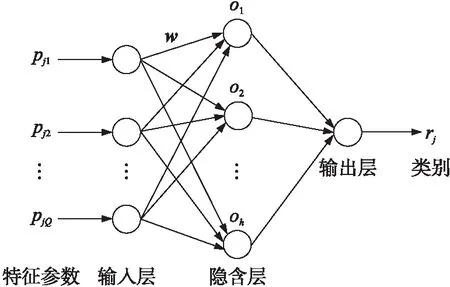
圖8 ELM的網絡結構

由于ELM隱含層與輸入層的連接權值和隱含層閾值是隨機生成的,并且可能存在參數為0的無效節點,其訓練結果具有隨機性,使用優化算法優化ELM能夠提高其準確率和泛化能力。

差分進化(differential evolution,DE)算法是在遺傳算法的基礎上提出的,具有能夠快速收斂并且不易陷入局部最優的優點。在確定ELM隱含層節點數目后,利用差分進化算法對ELM的隱含層輸入權值和閾值進行優化能夠提高ELM的性能,具體過程如下:

①設置初始參數,確定ELM的隱含層節點個數和DE算法的種群大小、種群迭代次數、變異因子、交叉概率等參數;

②隨機生成初始種群,種群中的個體作為ELM的隱含層節點參數和,以ELM測試集的預測正確率為適應度函數,計算每個個體的適應度值;

③對每個個體進行變異、交叉和選擇操作,得到新一代種群;

④重復過程③直到達到指定的迭代次數;

⑤輸出最優的隱含層節點參數和,訓練性能最優的ELM。

本文提出的FPCA和DEELM算法結合的協調機械臂性能故障診斷模型如圖9所示。首先采集不同故障類型下協調機械臂協調過程中的支臂角位移信息,以函數的視角對支臂角位移信息進行分析,將其表示為平滑的函數曲線,利用FPCA方法提取曲線特征參數作為故障特征集。將訓練樣本的故障特征集與對應的分類標簽作為ELM的輸入與輸出進行訓練,同時利用DE算法對ELM的隱含層參數和進行優化,得到性能最優的ELM作為故障識別器。然后對待識別樣本進行FPCA特征提取,將特征參數輸入到訓練好的DEELM中,對待識別樣本進行診斷測試。

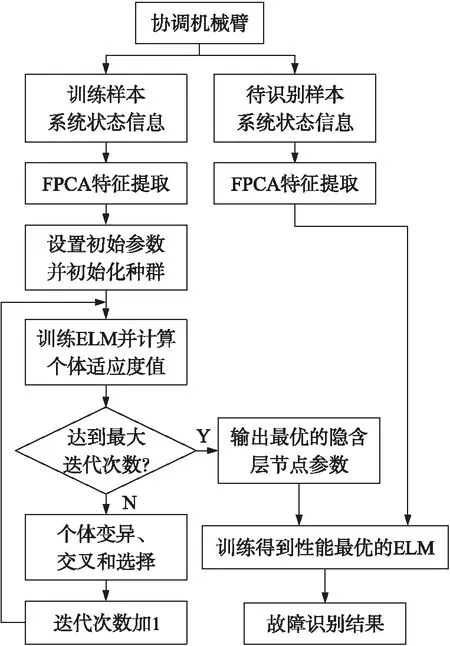
圖9 故障診斷模型

4.2 診斷結果

按照圖9所示的故障診斷流程,將FPCA提取的150組訓練樣本的支臂角位移曲線特征參數作為DEELM的輸入參數,對應的故障類型作為輸出參數,設置隱含層節點數為30,DE算法中種群個數為100,變異因子為1,交叉概率為0.7,最大迭代次數為50,進行DEELM訓練,得到最優的DEELM后對42組測試樣本進行診斷測試,同時利用ELM進行診斷測試作為對比。為了不失一般性,進行了10次測試,結果如表2所示。

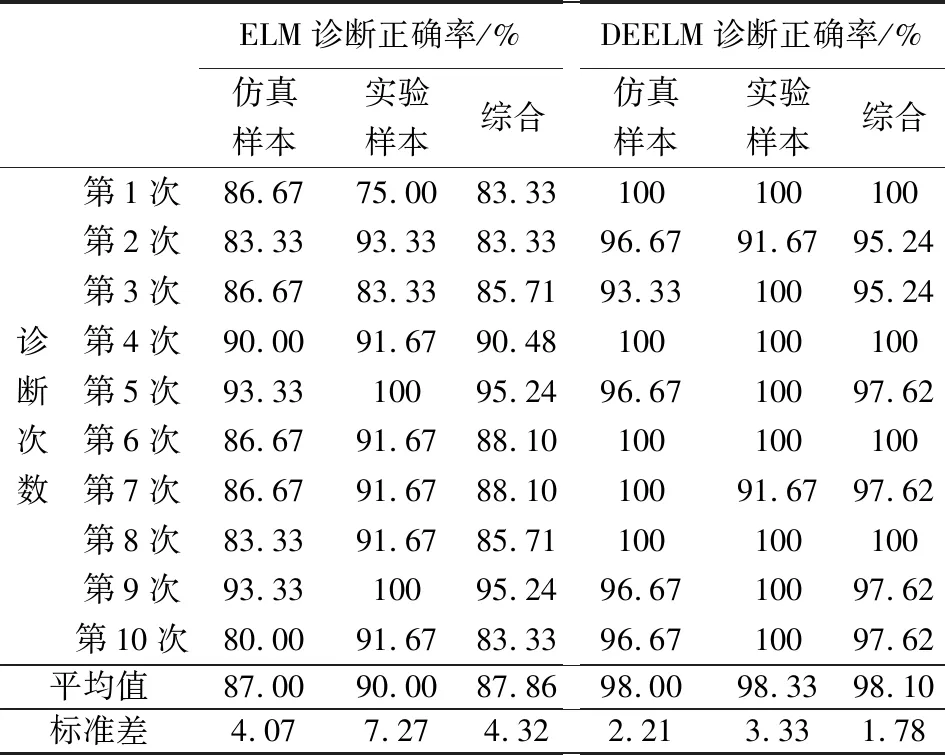
表2 10次故障診斷正確率

由表2可知,DEELM診斷正確率的平均值比ELM高,標準差比ELM小,表明通過DE算法優化ELM能夠提高ELM的診斷正確率,并且其性能更加穩定。DEELM對30組仿真樣本和12組實驗樣本的診斷正確率分別達到98.00%和98.33%。

表3給出了利用DEELM的10次診斷測試結果中各種故障類型的診斷正確率平均值,可以看出6種故障類型中沒有診斷正確率明顯低的情況,造成個別樣本診斷錯誤的原因可能是訓練樣本故障特征集的不完備性導致的。診斷結果表明,本文提出的FPCA與DEELM結合的方法能夠實現協調機械臂的性能故障診斷。

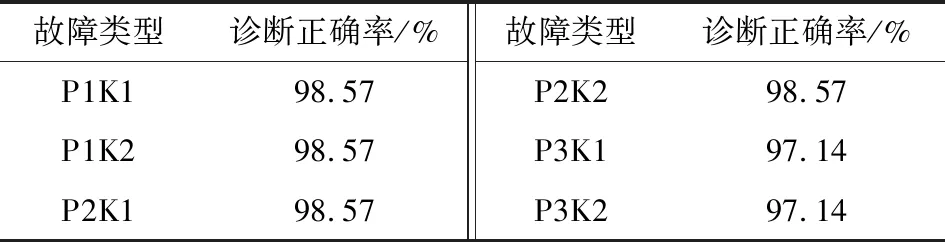
表3 6種故障類型10次診斷正確率平均值

5 結束語

本文針對彈藥協調機械臂定位精度超差的性能故障,提出了一種基于FPCA和DEELM的故障診斷方法。

①包含故障參數的協調機械臂動力學解析模型能夠近似表示真實的協調機械臂系統,并且便于獲取大量仿真故障樣本數據,利用協調機械臂實驗臺架進行模擬故障試驗能夠獲取真實故障樣本數據。

②協調機械臂發生性能故障會引起支臂角位移信號的變化,FPCA能夠有效提取支臂角位移信號中的故障特征成分,所提取的特征參數對6種故障類型的分類效果較好。

③DEELM具有比ELM更穩定的性能,基于DEELM的10次故障診斷測試,仿真樣本和實驗樣本的診斷正確率分別為98.00%和98.33%,表明該方法能夠對協調機械臂性能故障進行有效診斷。