二維趨化-Navier-Stokes方程的全局吸引子①
劉婷熙,范小明
西南交通大學 數學學院, 成都 611756
趨化現象最早在文獻[1-2]中提出, 描述的是生物學中由于化學物質的影響, 細胞進行定向運動的現象. 眾所周知, 細菌細胞一般是生活在各種各樣的粘性流體當中的, 所以近十年來趨化-Navier-Stokes方程[3-7]已經成為生物學家和數學家們比較關注的數學模型. 對于趨化-Navier-Stokes方程, 前人關于它在不同邊界條件下解的存在情況已有了很多研究[8-12]. 但是對于該系統吸引子的存在性的研究甚少. 本文主要討論二維有界域下的趨化-Navier-Stokes方程的全局吸引子. 趨化-Navier-Stokes方程如下:
(1)
(2)
(3)
(4)
下面是這個方程的初邊值條件:
n(x, 0)=n0(x),c(x, 0)=c0(x),u(x, 0)=u0(x),x∈Ω
在這個模型中,Ω?R2是一個帶有光滑邊界Γ: =?Ω的有界區域. 其中ν(x)是x∈Γ上的單位外法向量,φ是重力勢并且有φ∈L∞(Ω), Δφ=0,n表示細菌的種群密度,c代表化學濃度,p和u=(u1,u2)分別代表流體的壓力和速度. 設n(x,t),c(x,t)是關于空間和時間t>0的連續函數, 因為c是化學濃度, 故可設
再設f,g可導,f(0)=0,g(0)=0并滿足下列條件:
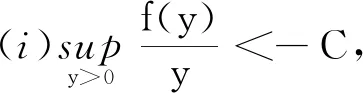

假設細菌和化學物質在一種不可壓縮的流體(如水)中求解, 利用Navier-Stokes方程中的速度u來模擬其流動, 由于重力勢的存在, 細菌細胞的重量將會影響流體的流動.
本文主要包含了以下幾個部分.
第1部分, 給出了半群和吸引子的定義、 吸引子的存在性定理; 討論了n,c是正解及解的適定性, 從而方程(1)-(4)決定了一個解半群.
第2部分, 證明趨化-Navier-Stokes方程(1)-(4)所對應的解半群在所研究的空間上存在正向不變的有界吸收集. 前人在處理這部分時是將趨化-Navier-Stokes方程看作一個整體來證明其系統的吸收性, 但由于方程(1)-(4)的復雜程度, 采用整體法無法處理其吸收性. 因此我們可以利用此方程的強耦合性, 將它分成3部分來處理. 首先利用能量估計等方法證明化學濃度c的吸收集是存在的, 再從c的吸收集出發證明細菌種群密度n的吸收集存在, 最后由n的吸收性證明了流體速度u的吸收集存在, 綜上所述得到了(n,c,u)的吸收集是存在的.
第3部分, 證明方程所對應的解半群是一致漸近緊的. 首先得到u的光滑性, 再利用方程的強耦合性, 通過u的光滑性得到c的光滑性, 再由u的光滑性得到n的光滑性, 最后利用半群性質, 得到解半群在所研究的空間上是一致漸近緊的.
1 預備知識
本章節將會給出一些證明所需的基本定義和定理.

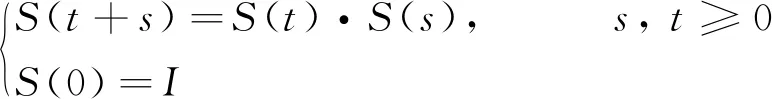
則稱S(t)為算子半群.
定義2[13]如果緊集A滿足下面的條件:
1) 不變性: A是半群S(t)作用下的不變集, 即S(t)A=A, ?t≥0;
2) 吸收性: A吸收H上的所有有界集. 即對于任意一個有界集B∈H, 這里的B滿足
3) A有一個開鄰域U, 使得對于U上的任意一個n0, 當t→∞時, 所有從n0出來的軌跡S(t)n0都收斂到A. 即當t→∞時, dist(S(t)n0, A)→∞, 則稱這個緊集A為半群S(t)的一個吸引子. 如果A還吸收相空間H, 則稱A為全局吸引子.
引理1[13]設{S(t)}t≥0是一個算子半群, U?H是一個開集, 并且
1) B是U上的一個吸收集;
2)S(t)是一致緊的(對于充分大的t), 則B的ω-極限集A=ω(B)是U上的一個緊的全局吸引子.
引理2若(n,c,u)是方程(1)-(4)在Ω×[0,T], ?T>0中的弱解, 則
n(x,t)>0,c(x,t)>0 a. e. (x,t)∈Ω×[0,T]
證由文獻[12]可知方程(1)-(4)在沒有f(n),g(c)這兩項時, 它的解n(x,t)>0,c(x,t)>0是成立的, 則可以推出
其中A(t)=-u·+Δ-(c·+Δc), 所以因此有
又因為f(0)=0, 所以由中值定理可以得到
則
同理可證c(x,t)>0.

‖u‖Lq(Ω)≤C‖u‖Lp(Ω)


其中


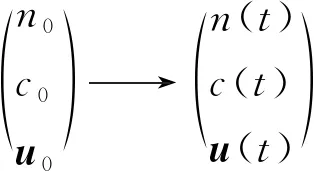
該定理給出了解的適定性, 其證明主要利用Faedo-Galerkin方法[13], 與文獻[11]類似, 本文不做過多贅述. 再結合引理2, 我們得到n,c>0.
由定理1足以在空間H上定義連續的算子半群{S(t)}t≥0:
下面將利用文獻[13-15]證明在空間H上半群{S(t)}t≥0存在全局吸引子A.
2 H上吸收集的存在性
首先證明在H上存在有界吸收集, 其過程需要在相應的空間中對解進行估計.
引理5設B1是L2(Ω)中的任一有界集,c是從B1中出發的方程(2)的一個解. 存在常數γ1>0和時間t1=t1(B1)>0, 當t≥t1時,
證由條件(ii)可得存在常數β∈(0,λ1)和充分大的正常數K1, 使得
g(c)≤(λ1-β)c+K1
(5)
對方程(2)的兩邊分別與c作L2(Ω)的內積
由(5)式得
(6)

(7)

(8)
對(8)式使用Gronwall不等式, 有

(9)
引理6設B2是L2(Ω)中的任一有界集,n是從B2中出發的方程(1)的一個解. 存在常數γ2>0和時間t2=t2(B2)>0, 當t≥t2時,
證設L2(Ω)上一球形鄰域包含B1, 其圓心為零點, 半徑為γ1. 由引理5知,c從L2(Ω)的有界集出發, 在時刻t1后將一直在有界集B1中. 不妨設c總在B1中.
對方程(1)的兩邊分別與n作L2(Ω)的內積, 得到
由化學濃度c的有界性和連續性得
再由條件(i)可得f(n)≤-Cn+K1,K1是一個充分大的常數, 則
對K1‖n‖L1使用Young不等式得
因此
(10)
由Gronwall不等式得
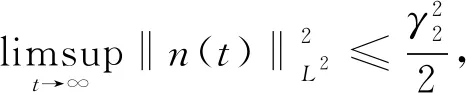
(11)

證設L2(Ω)上一球形鄰域包含B2, 其圓心為零點, 半徑為γ2, 由引理6知,n從L2(Ω)的有界集出發, 在時刻t1+t2后仍在有界集B2中. 不妨設總在B2中.

此時壓力項將會消失, 得到
(12)
由(19)式
利用Gronwall不等式,

(13)
綜合(9), (11), (13)式可以得到在H上以零點為圓心,RB=γ1+γ2+γ3為半徑的有界閉球B=B(0,RB)是(n,c,u)的有界吸收集, 且是正向不變的, 即H上任意有界集B?B(0,RB), 經過時間t*=t1+t2+t3后, (n,c,u)進入B中且不再離開. 故由引理5- 7得到.
定理2方程(1)-(4)生成的解半群{S(t)}t≥0在空間H上存在正向不變的有界吸收集.
3 解半群{S(t)}t≥0一致漸近緊
設B是{S(t)}t≥0在H中的正向不變集. 設(n,c,u)是方程(1)-(4)的整體解. 現證明從B出發, 方程的解最終都進入K的有界集, 從而得到解半群{S(t)}t≥0是一致漸近緊的.
引理8?r>0, 存在常數γ4(r)>0, 當t≥r時, 有
證對(12)式從t到t+r上積分, 有
(14)
讓方程(3)在Ω上與-Δu作內積, 得
利用引理4和Young不等式
再利用(13)式可得
(15)
(16)
由(15),(16)式得
根據(11)式得

這意味著對所有的t≥r,
(17)
引理9?r>0, 存在常數γ5(r)>0, 當t≥r時, 有
證將(7)式從t到t+r上積分, 有
(18)
讓方程(2)在Ω上與-Δc作內積得
利用Young不等式、 H?lder不等式和引理3得
由(17)式可得
(19)

(20)

結合(19)-(20)式得到如下不等式
(21)
對(21)式從0到r上積分
由(18)式得


這意味著對所有的t≥r
(22)
引理10?r>0, 存在常數γ6(r)>0, 當t≥r時, 有
證對(10)式從t到t+r上積分, 有
由(11)式可得
(23)
讓方程(1)在Ω上與-Δn作內積
利用Young不等式、 H?lder不等式和引理3
(24)
由(17)和(24)式可得
(25)
這里C4是一個充分大的正常數.
(26)

(27)
由(25)-(27)式可得
(28)
對(28)式從0到r積分, 得
由(23)式得

這意味著對所有的t≥r,
(29)
定理3方程(1)-(4)生成的解半群{S(t)}t≥0是一致漸近緊的.
證設K上以零點為圓心,RM=γ4+γ5+γ6為半徑的有界閉球M=B(0,RM). 由引理8、 引理9和引理10知(n,c,u)從H中的正向不變集B出發, 經過時間r后, 進入K中的有界集M. 而K緊嵌入到H中, 從而得到解半群{S(t)}t≥0在H中是一致漸近緊的. 證畢.
由定理2和定理3以及引理1得到方程(1)-(4)在H上存在緊的全局吸引子.

