數列求和問題面面觀

薛紅利

(吉林省長春市第六中學)

數列求和是高考中比較常見的考點,有時以解答題的形式出現,有時以選擇題或填空題的壓軸題形式出現.數列求和問題除了直接利用等差數列或等比數列的求和公式外,經常還通過裂項相消法、錯位相減法、分組轉化法、并項求和法等方法來求解.

1 裂項相消法

破解策略 裂項相消法求和需過的“三關”:第一關是定通項,即會利用求通項公式的常用方法求出數列的通項公式;第二關是巧裂項,即能將數列的通項公式準確裂項;第三關是消項求和,即把握消項的規律,準確判斷剩余的項是哪幾項,從而順利求和.

2 錯位相減法

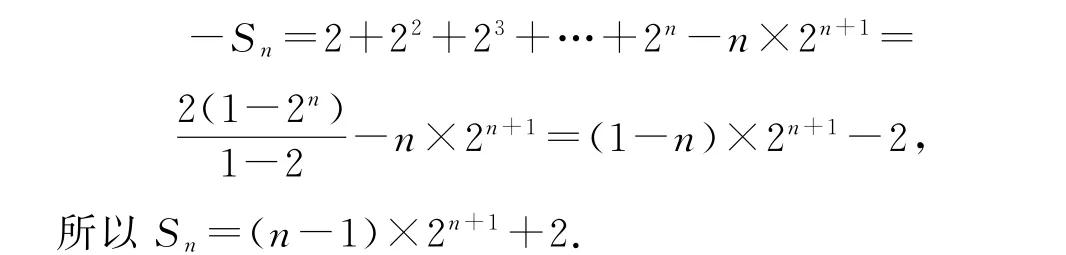
破解策略 應用錯位相減法求和的關鍵:一是判斷模型,即判斷數列{an},{bn}是不是一個為等差數列、一個為等比數列;二是錯開位置,為兩式相減做準備;三是相減,相減時一定要注意最后一項的符號,在解題時常在此處出錯,一定要小心.

3 分組轉化法

當一個數列既不是等差數列,也不是等比數列時,可以將這個數列合理拆分,再重新組合,變成幾個可以利用特殊數列進行求和的部分(經常采用分組轉化法加以分別求和),然后再合并即可達到數列求和的目的.

破解策略 分組轉化法求和需過的“四關”:第一關是轉化,即將已知條件轉化為數學語言;第二關是解方程,即利用方程(組)的思想求出等差數列或等比數列中的基本量;第三關是分組求和,即觀察數列通項公式的特征,若其是由若干個簡單數列(如等差數列、等比數列)的通項組成,則求和時可用分組求和法,把數列分成幾個可以直接求和的數列;第四關是用公式法求和,對分組后的各個數列求和,觀察各個數列的特點,利用等差數列、等比數列的前n項和公式求和.

4 并項求和法

在解決一些涉及三角函數或與絕對值有關的數列求和問題時,經常根據相關數列的特征,先將數列的每兩項(或多次)合并到一起,再轉化為熟悉的等差數列或等比數列進行求和處理.這種方法常適用于擺動數列的求和應用問題.

破解策略 用并項求和法對數列進行求和,關鍵是將一個數列分成若干段,然后分別利用等差數列或等比數列的求和公式或其他求和方法求解各分段數列.利用并項求和法求解數列問題的常見類型:一是數列的通項公式中含有絕對值符號;二是數列的通項公式中含有符號因子“(－1)n”等相關的形式.