具有混合執行器故障的多智能體分布式有限時間自適應協同容錯控制

張 普, 薛惠鋒, 高 山, 左 軒

(西北工業大學自動化學院, 陜西 西安 710129)

0 引 言

近年來,多智能體系統協同控制技術在人工智能發展中具有重要作用,吸引了大量學術界和工業界學者的研究目光。其在軍事和民用方面均有廣泛的應用,例如無人機集群、機器人協作,森林火災救援等方面。這些應用對多智能體系統協同控制技術的可靠性和控制精度均有較高的要求,然而,隨著智能體系統的復雜程度逐漸增大,系統發生故障的可能性也越來越頻繁。尤其是執行器故障問題,如果不能及時地進行有效的容錯處理,不僅智能體系統的協同性能受到影響,甚至會導致整個目標任務的失敗。基于此,本文著眼于研究多智能體系統中執行器發生故障時的協同容錯控制技術。

目前,學者們基于先進控制理論已經提出了很多關于具有執行器故障的多智能體系統的容錯控制方法。文獻[4]采用一種分層容錯控制策略,底層為故障檢測、隔離及重構,上層為預測與補償故障,為一類四旋翼無人機編隊解決了執行器卡死故障。文獻[5]針對嚴參數反饋非線性系統,提出了一種完全分布式自適應容錯控制器,解決了部分失效型執行器故障問題。文獻[6]設計了一種魯棒自適應容錯控制律,補償執行器偏置故障和部分失效執行器故障。文獻[7]提出了一種事件觸發容錯控制方法,用于解決執行器故障問題。文獻[8]基于自適應滑模觀測器,構建了一種分布式協同容錯控制器,補償執行器失效故障和偏置故障。文獻[9]提出了一種基于在線重構的自適應協同容錯控制策略,用于補償異構多智能體系統的時變失效故障和加性執行器故障。文獻[10]采用delta算子的方法設計了一種H/H模型預測容錯控制方案,解決時變執行器故障問題。文獻[11]設計了一種基于虛擬執行器的協同容錯策略,通過對稱控制器和觀測器相結合,來隱藏執行器故障對系統的影響。在上述研究中,大多是基于執行器故障模型中具有一種或兩種類型故障展開的研究。然而,在實際工程中,非線性多智能體的執行器故障類型不僅未知,而且不止一種或兩種,并可能伴隨有混合故障類型的現象。此外,除了未知故障問題,系統模型中的控制增益參數一般也不具有先驗性。因此,有必要針對同時具有未知混合執行器故障及未知動態控制增益的非線性多智能體系統的容錯控制問題展開深入研究。

值得關注的是,上述研究主要針對未知故障和未知控制增益參數所引起的多智能體系統不穩態性能,沒有涉及到瞬態性能問題,即有限時間內穩定問題。而在諸多有關多智能體系統的實際工程應用中,諸如無人機、航天器以及機器人的姿態等,不僅需要有效克服執行器故障所引起的系統不穩定,并且需要系統在有限時間收斂到零或者零點的鄰域內,最終使多智能體系統實現漸近穩定。因此,盡管上述文獻提出了很多解決多智能體系統執行器故障的容錯控制方法,然而很少能夠在有限時間內有效地解決具有混合執行器故障和未知控制增益的多智能體系統協同容錯問題,并且保持沿預設編隊軌跡運動。

因此,本文針對一類高階嚴反饋非線性多智能體系統,基于動態面控制和自適應反推技術相結合,提出了一種自適應協同容錯控制策略,解決系統模型中含混合執行器故障和不確定非線性參數問題。主要貢獻有以下幾點:

(1) 考慮了混合執行器故障,針對一類更具一般性的具有未知混合執行器故障的干擾高階非線性多智能體系統,提出了一種新穎的基于動態面控制的自適應容錯控制策略。在文獻[4-11]中,作者僅能解決一種或兩種執行器故障。與上述文獻相比,本文所提方法同時考慮了不同類型的執行器故障,在拓寬應用潛力方面具有重要意義。

(2) 與現有文獻的神經網絡估計技術相比,本文所提的徑向基函數神經網絡(radial basis function neural networks, RBFNNs)自適應技術,不僅能夠在線精確估計不同類型故障,實時補償未知的混合執行器故障,并對系統模型中的未知動態參數實現局部最優估計。因此,所提方法在混合故障情形下依舊能夠保持良好的容錯能力。

(3) 與現有方法相比,所設計的分布式有限時間控制器,基于有限時間理論與一致性協議,能夠確保多智能體系統在有限時間達到穩定狀態,并以預設隊形運動。

1 預備知識

1.1 圖論及通訊條件

一個有向網絡可以用=(,,)表示,是用于建立智能體之間通訊模式的數學工具。其中={,,…,}是個節點的集合,?×是有向邊的集合,=()×∈×是加權鄰接矩陣,滿足>0。而且,中有向邊表示一個有序點對(,),即從到的有向信息流,也就是說節點可以獲得節點的信息。當且僅當中存在有向邊(,),鄰接矩陣中的每個元素>0,否則=0(≠;,=1,2,…,)。此外,本文均不考慮自環,即=0(=1,2,…,)。若鄰接矩陣滿足=,則稱該特殊情況下的=(,,)為無向網絡。

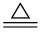
信息交互是多智能體系統實現協同控制的必要條件。

1.2 RBFNNs理論

()=()+()

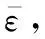
(1)

式中:∈?表示RBFNNs的輸入向量;=[,,…,]表示權重向量;表示隱藏層;()是徑向基函數向量。

本文所選的徑向基函數為高斯函數,其表達式為

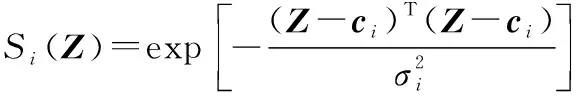
(2)

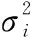
理想的權重是由最小估計誤差優化而來。

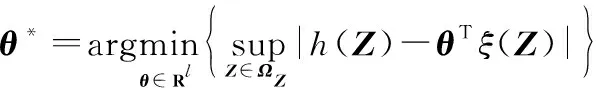
(3)

式中:表示實數。基于理想權重,()是給定的光滑函數,對式(1)進一步求解,可得未知的非線性函數如下:

()=()+()

(4)

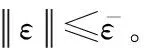
1.3 有限時間理論

原點是有限時間穩定平衡的,當且僅當原點是Lyapunov穩定且存在原點的開鄰域?和一個被稱為設定時間的正定義函數():→使得對于所有(0)∈{0},有

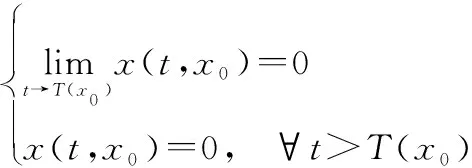
(5)

此外,如果原點在=上是有限時間穩定的,則原點是全局有限時間穩定平衡的。而且,原點的有限時間穩定性也意味著原點的漸近穩定性。

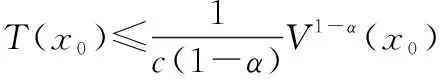
(6)

對于非線性系統,假設存在一個連續光滑正定函數()和標量>0, 0<<1,>0使得

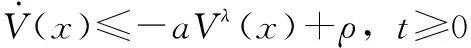
(7)

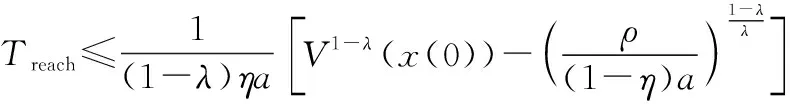
(8)

對于,∈,0<<1,有如下不等式成立:

(+)≤+

(9)

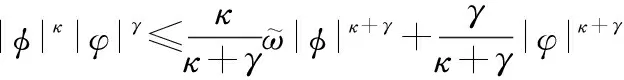
(10)

2 系統模型

2.1 執行器故障模型

智能體的執行器故障主要是由于智能體出現老化、損傷,通訊失效以及傳感器失效等形成部分失效故障、完全失效故障、偏置故障、卡死故障等4種故障,其數學模型如下:

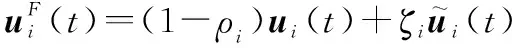
(11)

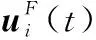
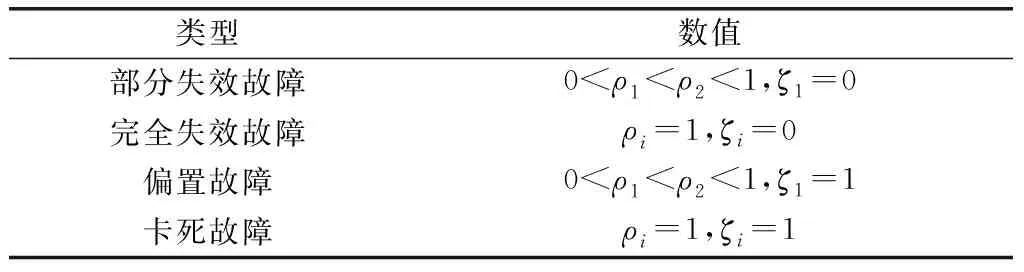
表1 執行器故障類型Table 1 Actuator failure types

綜合分析,可得系統執行器故障模型如下:

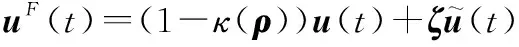
(12)

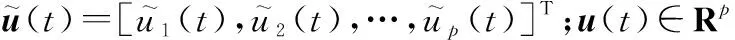
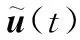
多智能體編隊系統在實現預期控制目標過程中,當某一個智能體的執行器出現部分失效故障時,多智能體系統由于通信的中斷,有可能引起執行器不能正常運行,表現為部分失效現象。

多智能體編隊系統預設的隊形編隊運動,每個智能體的軌跡均為一條光滑的函數,存在一個正常數,使得滿足以下緊集:

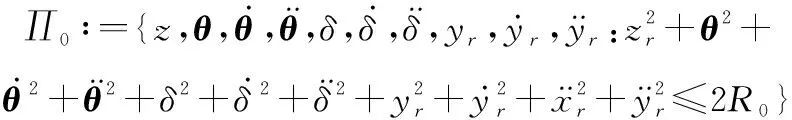
(13)

2.2 多智能體模型

考慮一類包含個智能體的多智能體系統,每個智能體具有不確定性的嚴反饋非線性動態性能,模型表示為

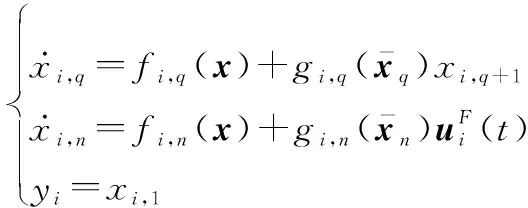
(14)

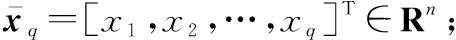
時變參考軌跡是連續有界的,則控制系統式(14)是一個閉環穩定系統且能夠追蹤給定的參考軌跡信號。

3 跟蹤控制律設計

基于執行器故障模型式(12)和系統模型式(14)進行容錯控制律設計,其過程如下。

定義跟蹤誤差:

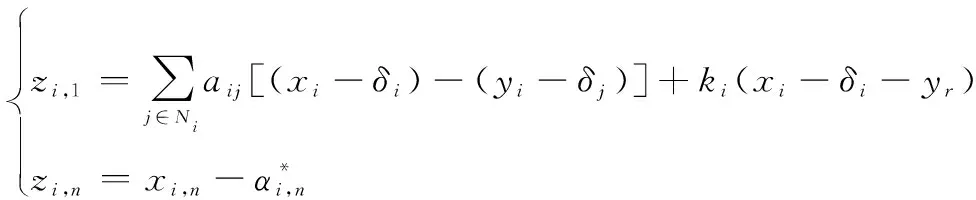
(15)

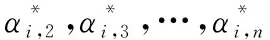
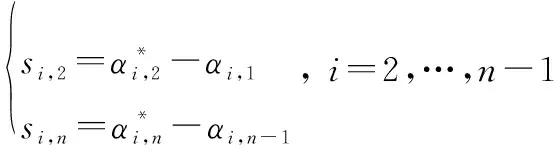
(16)

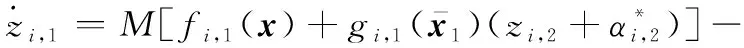
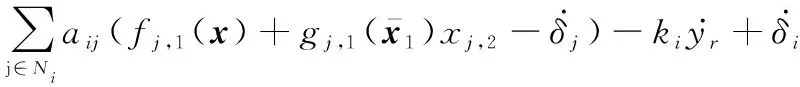
(17)

式中:=∑∈+。

根據RBFNNs,式(17)可進一步改寫為

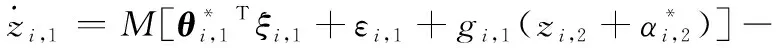
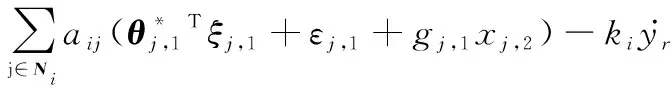
(18)

構建Lyapunov函數如下:

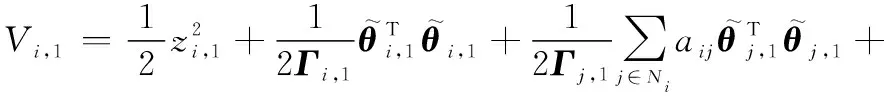
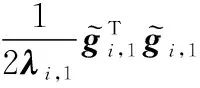
(19)

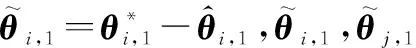
對式(19)時間求導,得

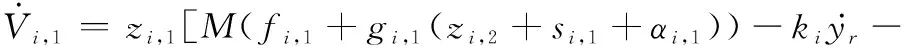
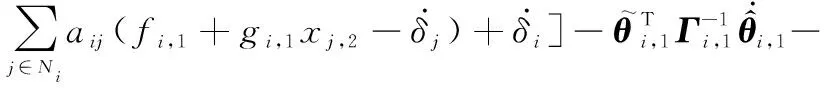
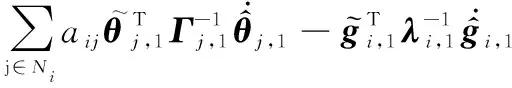
(20)

應用第12節的RBFNNs,對未知函數,1和,1逼近處理,得

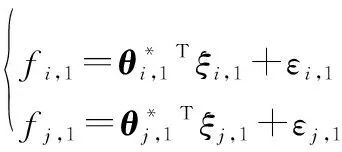
(21)

根據引理5和Young’s不等式,可知

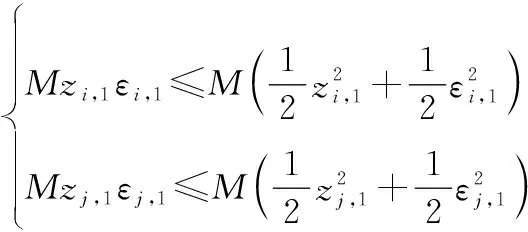
(22)

將式(21)和式(22)代入式(20),可得

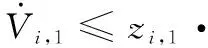
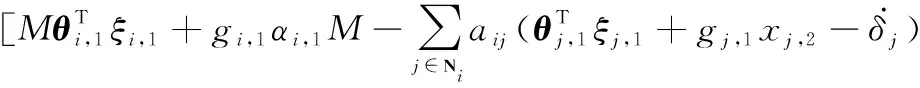
4）訓練方式、手段及步驟：將學生分成幾個小組（5人一組），每個小組確定說話的類型，小組內進行談論，要求每位學生都參與，說話時間至少3分鐘；小組訓練結束后，教師在隨機抽取各小組幾名學生，進行即興說話，學生和老師按照既定標準進行的評分和點評。

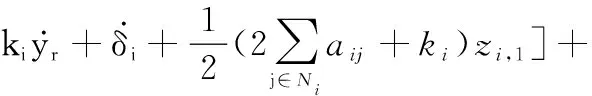
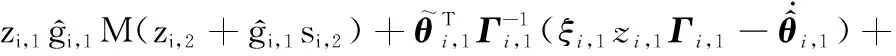
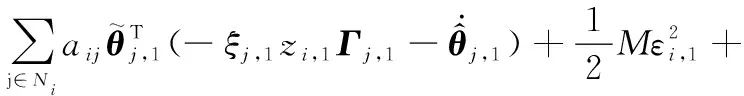
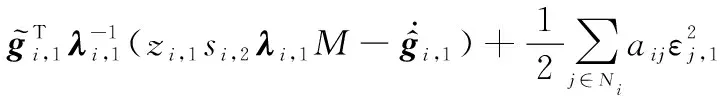
(23)

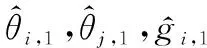
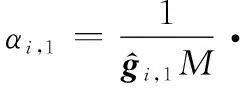
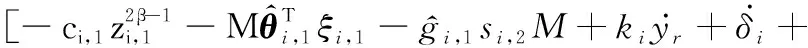
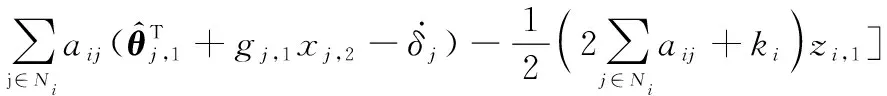
(24)

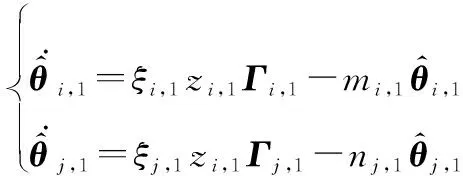
(25)

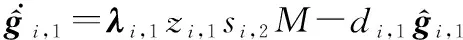
(26)

式中:,1、,1、,1、,,為設計常數。

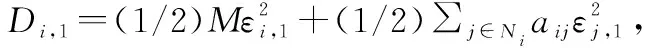
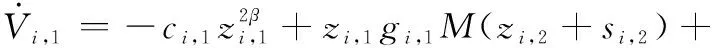
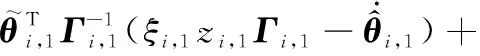
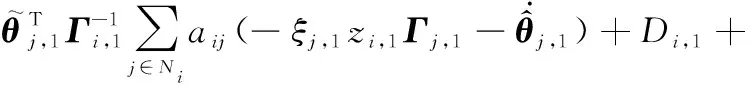
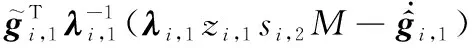
(27)

將式(25)和式(26)代入式(27),則有

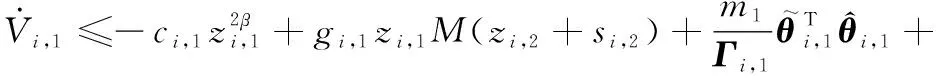
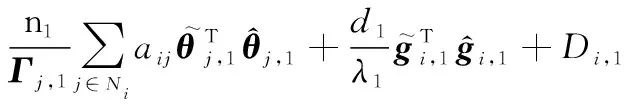
(28)

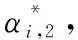
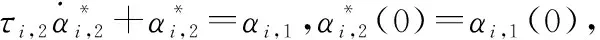
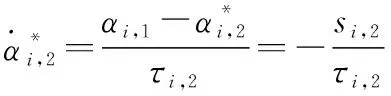
(29)

由此可知

(30)

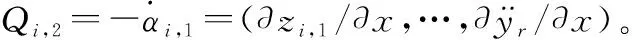
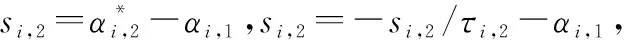
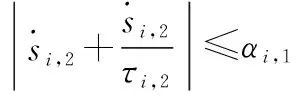
(31)

根據引理4和引理5,則有

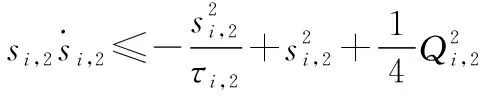
(32)

定義新誤差如下:

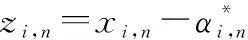
(33)

對式(33)求導,可得

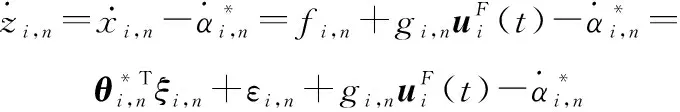
(34)

同理,選取構建Lyapunov函數如下:

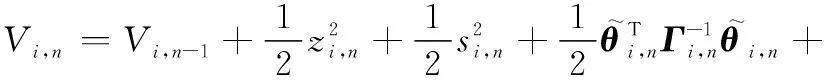
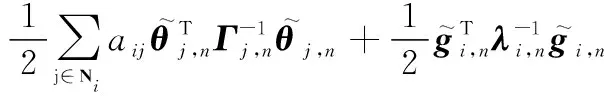
(35)

對式(35)時間求導,可得

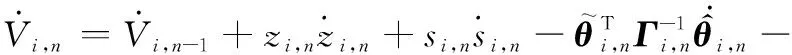
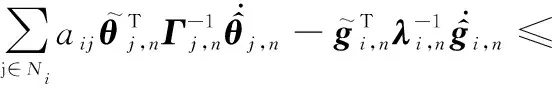
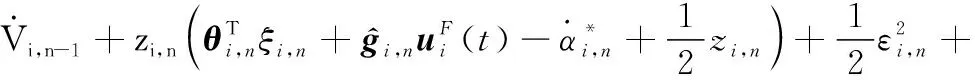
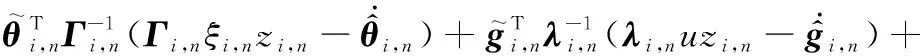
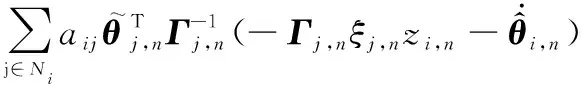
(36)

根據式(12),式(36)進一步化簡為

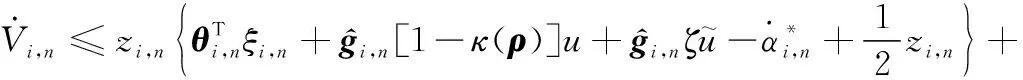
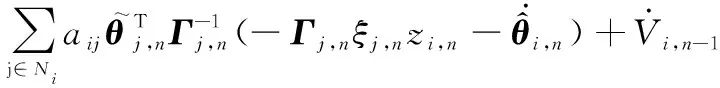
(37)

根據RBFNNs逼近理論,可得

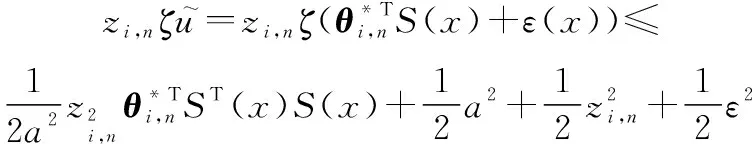
(38)

聯立式(37)和式(38),可得

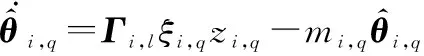
(39)

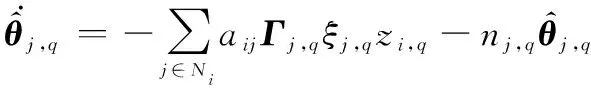
(40)

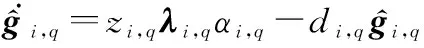
(41)

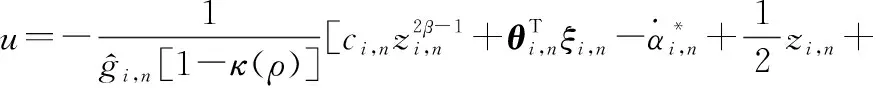
(42)

將式(39)～式(42)代入式(37),可得

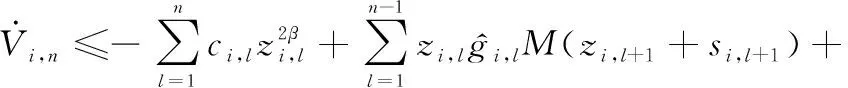
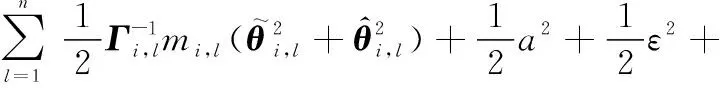
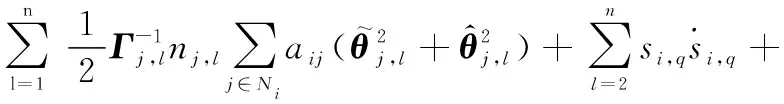
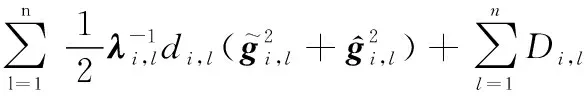
(43)

根據引理4和引理5,可得

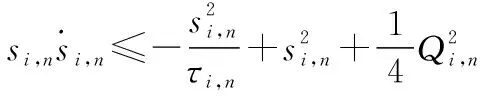
(44)

將式(44)代入式(43),則有

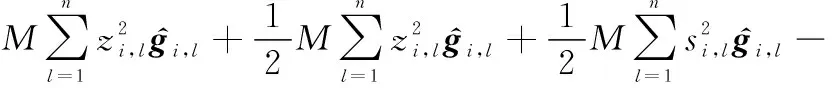
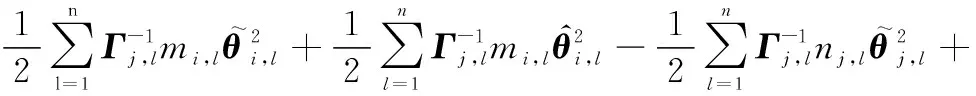
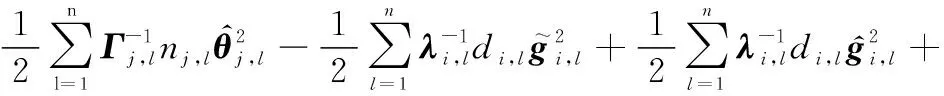
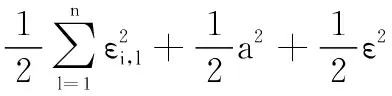
(45)

根據引理5,對式(45)進行變換,則有

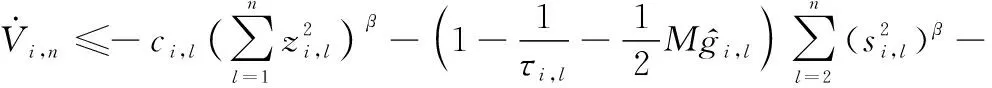
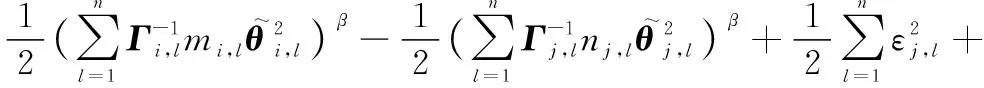
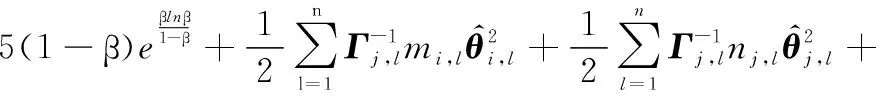
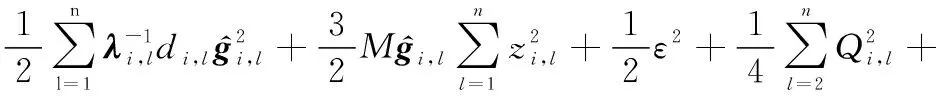
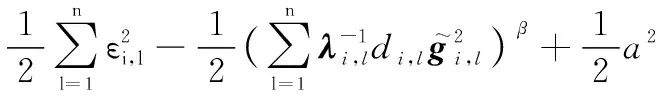
(46)

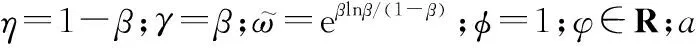
根據有限時間定理,式(46)可進一步簡化為

(47)

式中:

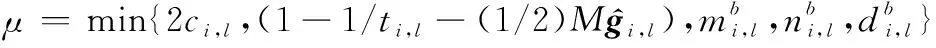
于是,可進一步得出給定時間如下:

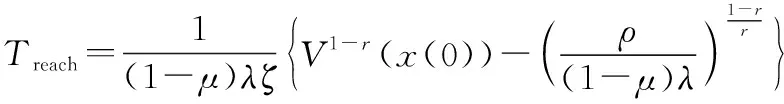
(48)

4 穩定性分析

高階非線性多智能體系統式(13)在滿足假設1至假設3的前提下,利用分布式動態面控制和分布式自適應控制,能保證控制系統目標的實現,即高階非線性多智能體系統式(14)的狀態能最終以預設隊形實現漸近一致追蹤的目的。

為了分析所設計控制律的穩定性,構建整個閉環系統的Lyapunov函數如下：

=1+2

(49)

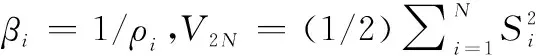
對式(49)求導,可得

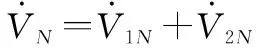
(50)

于是,可得

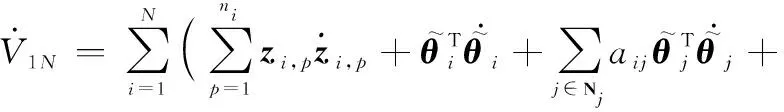
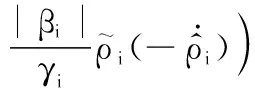
(51)

根據引理5、追蹤誤差式(15)、邊界誤差式(16)、RBFNNs式(1)以及有限時間理論式(5),式(51)可進一步重寫為

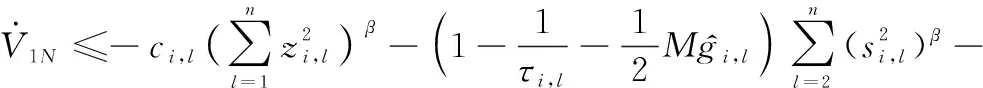
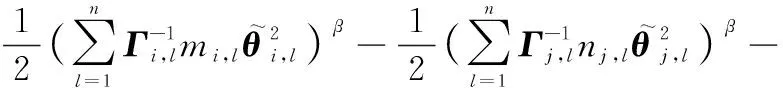
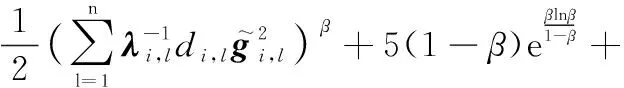
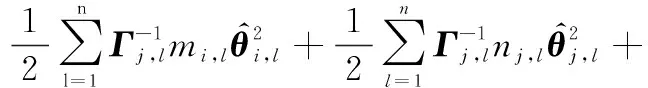
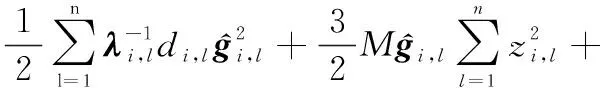
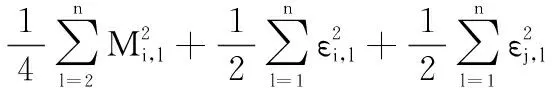
(52)

同理,2的導數如下:

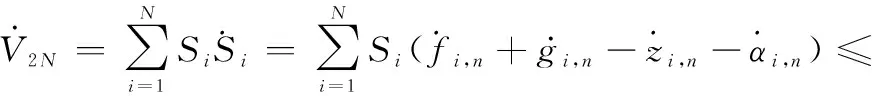
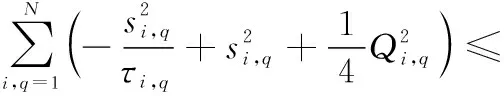
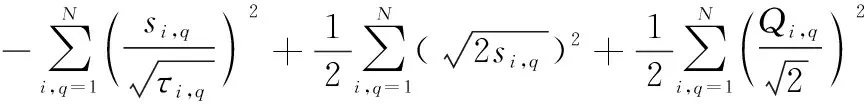
(53)

式中:

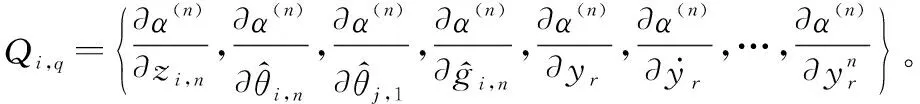
于是,聯立式(52)和式(53),可得

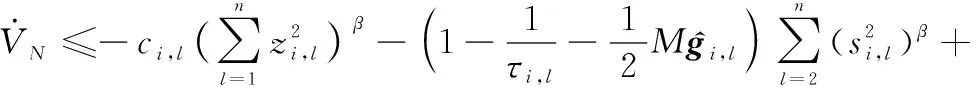
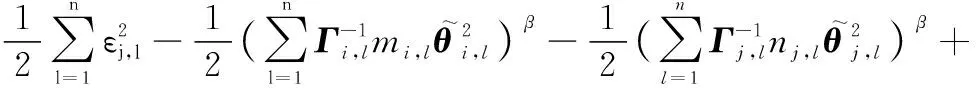
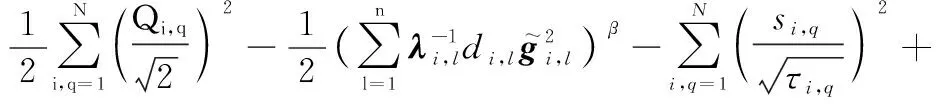
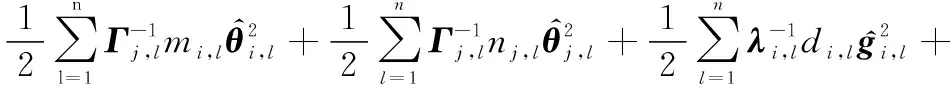
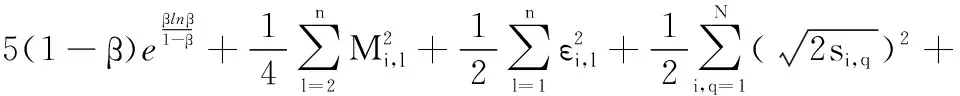
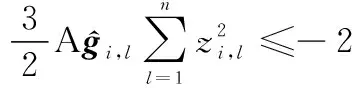
(54)

式中:

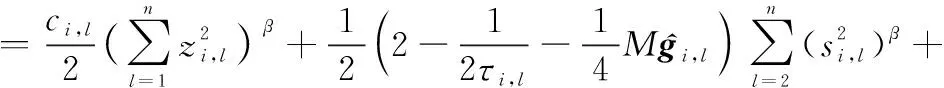
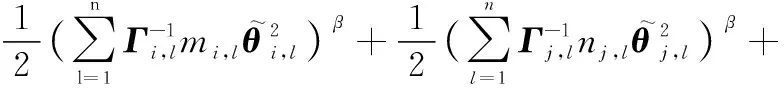
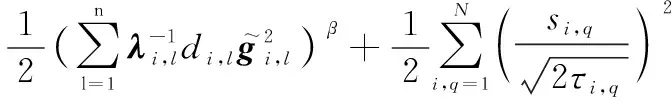
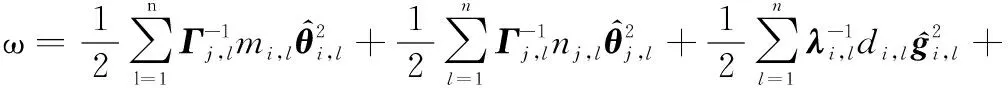
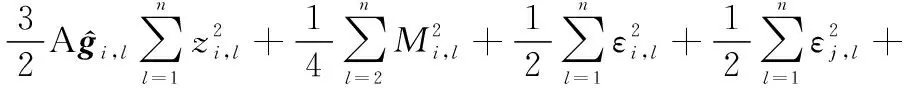
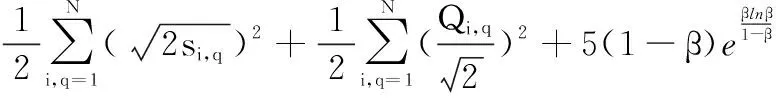
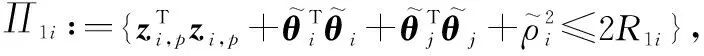
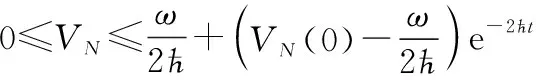
(55)

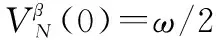
因此,當時間足夠大時,多智能體系統的跟蹤誤差,,…,在有限時間收斂,而且均為有界的,從而實現多智能體系統在執行器故障的情形下有限時間集結預設隊形,并保持該隊形追蹤運動目標。

證畢

5 仿真實驗

在本節中,采用由(=10)個智能體組成的多智能體系統有向拓撲結構,其中包括一個領航者和-1個跟隨者(見圖1)。

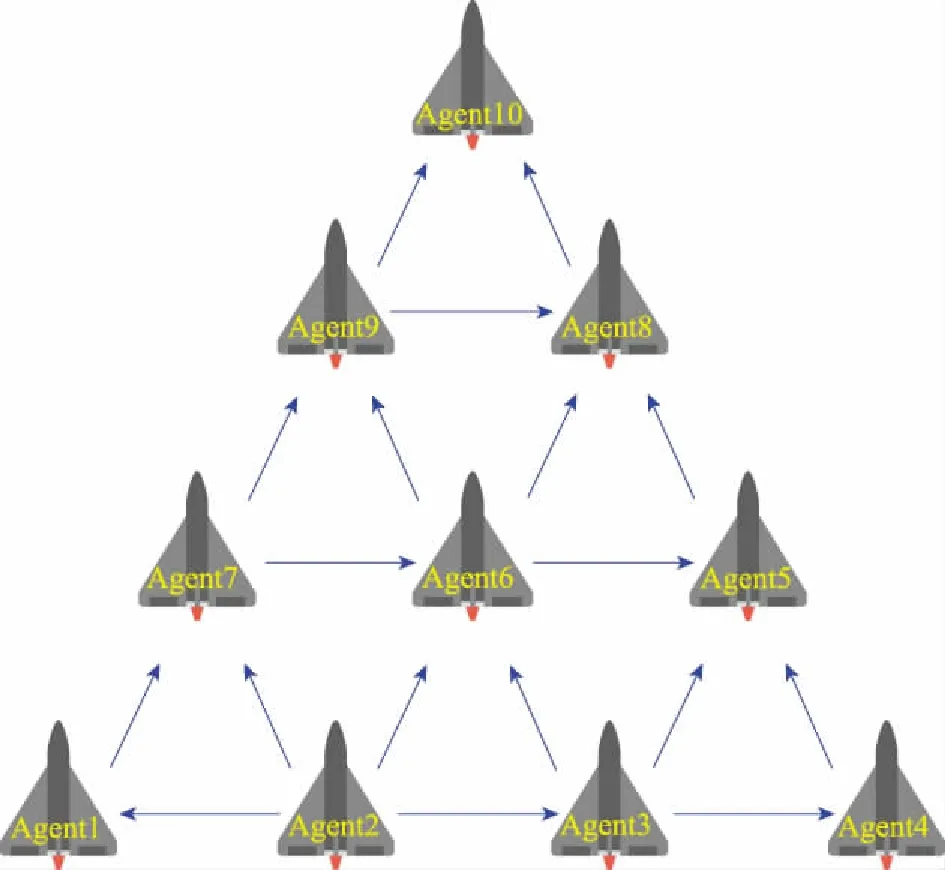
圖1 多智能體系統網絡拓撲結構圖(N=10)Fig.1 Multi-agent systems network topology diagram (N=10)

多智能體系統在執行器故障情形下編隊飛行過程中,需要彼此之間進行信息的交互與共享,才能實現協同飛行。根據第21節圖論知識,智能體#與智能體#之間信息存在信息的交互,則鄰接矩陣中的元素(,)=1,2,3,…,10取值取決于它們之間的方向,即=1,否則=0。基于此,可得鄰接矩陣和度矩陣:

于是,進一步可得拉普拉斯矩陣=-。同時,設定每個智能體的質量=10 kg,每個智能體的集結速度=2 m/s,集結的角速度=59°/s。期望的參考軌跡=2 cos,=98 m/s。此外,選取=002,根據式≥(2),可取=002。控制參數可選取為=15,=20,=30,=25;=002,=004,=002,=002;=diag{3},=diag{10},=diag{5},=diag{8};====0005;同時需要逼近的兩個參數為和,逼近的函數為,以及(,),重構函數(,)=(,5sin(15))。除此之外,多智能體系統的初始位置、線速度以及角速度,如表2所示。

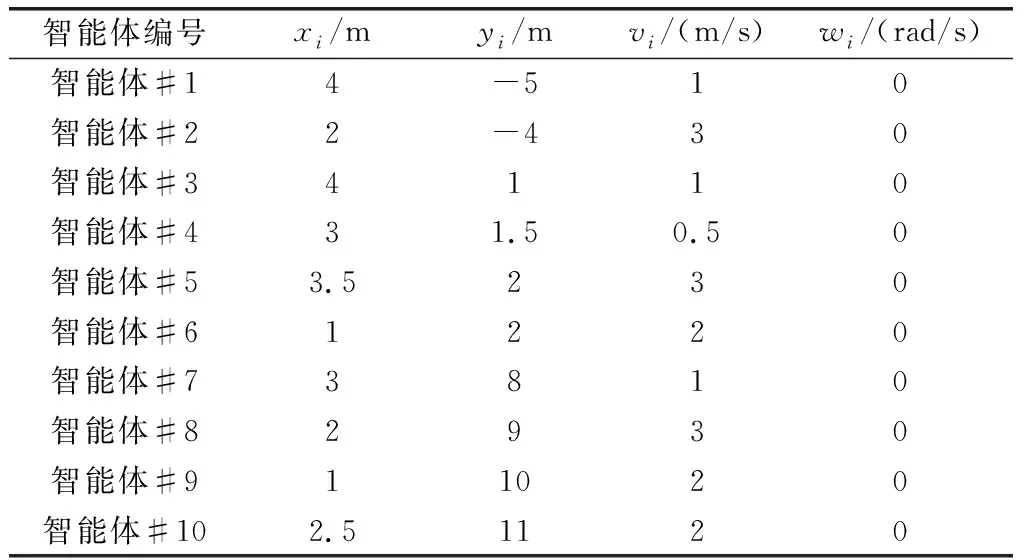
表2 多智能體系統的初始狀態Table 2 Initial state of the multi-agent systems

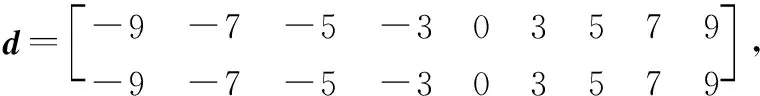
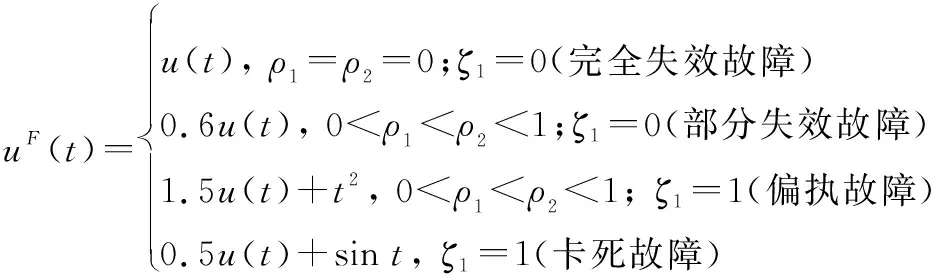
(56)

除此之外,在仿真過程中,考慮的兩個算例,如下所示。

考慮以下非線性系統

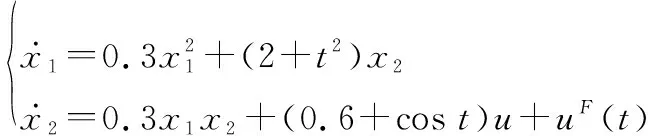
(57)

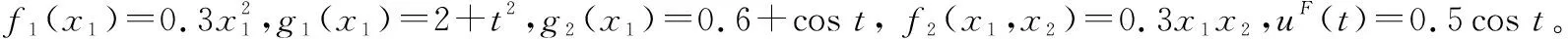
根據以上非線性系統、初始條件以及前述假設,其仿真結果如圖2～圖5所示。

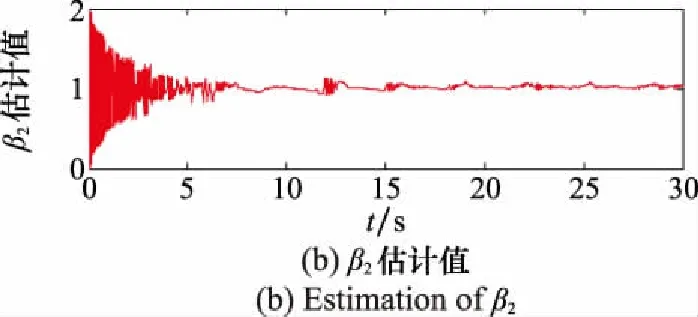
圖2 控制參數β1和β2的估計值曲線圖Fig.2 Estimation curves of control parameters β1and β2

圖3 f1/β1的神經網絡逼近Fig.3 Neural network approximation curve of f1/β1

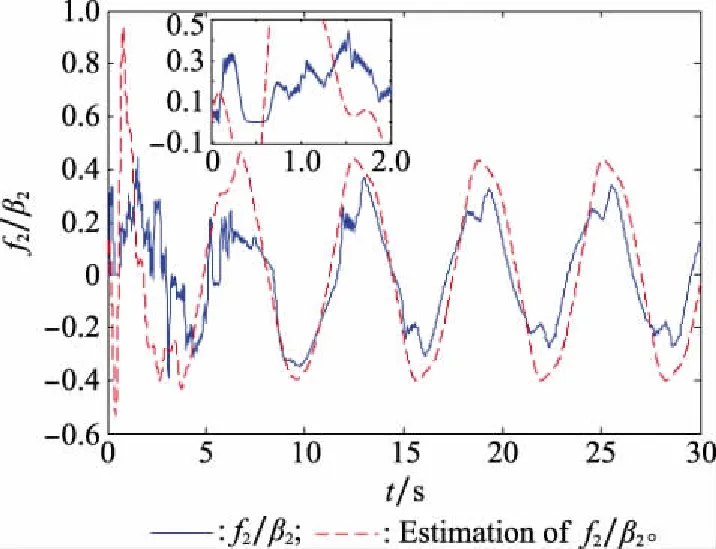
圖4 f2/β2的神經網絡逼近Fig.4 Neural network approximation curve of f2/β2

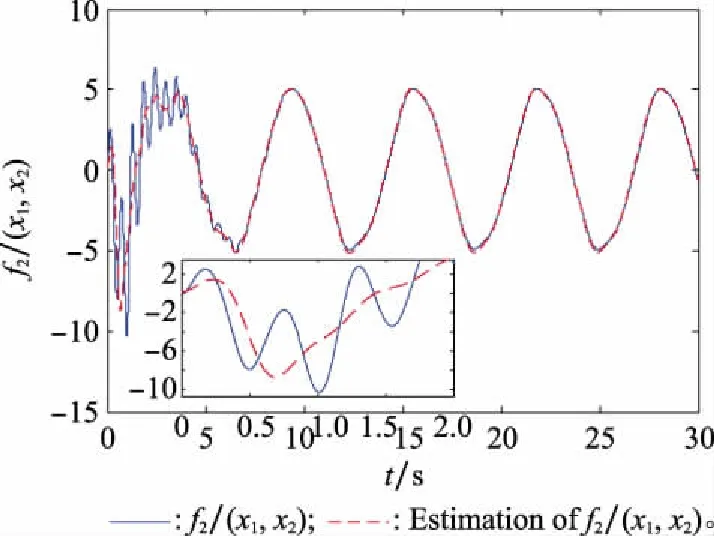
圖5 f(x1,x2)的神經網絡逼近Fig.5 Neural network approximation curve of f(x1,x2)

由仿真結果可知,所提出的RBFNNs可以有效逼近未知非線性項,使得在控制器設計過程中避免對高階系統多次求導。而且,對含有執行器故障的多智能體系統,具有良好的容錯效果。

為了進一步說明所設計的控制律的有效性,將其應用于由10個機器人組成的編隊,進行容錯控制研究,每一個機器人的動力學模型如下：

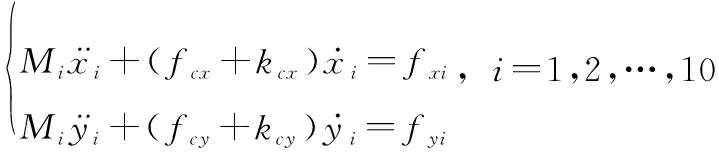
(58)

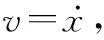
為了減少參數估計數量,作以下變換：

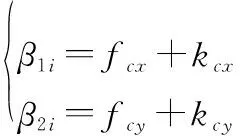
(59)

在本節中,采用相同的仿真環境,控制參數和初始條件,其仿真結果如圖6～圖9所示。

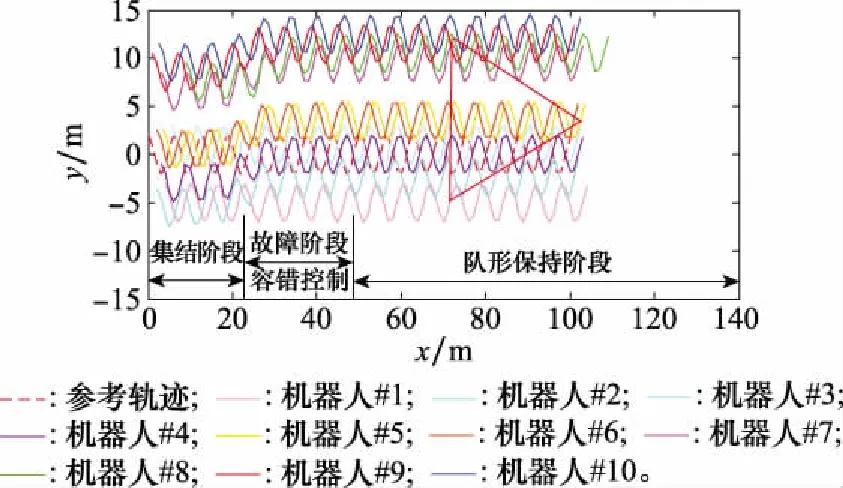
圖6 機器人編隊運動軌跡曲線圖Fig.6 Trajectory curve of robot formation

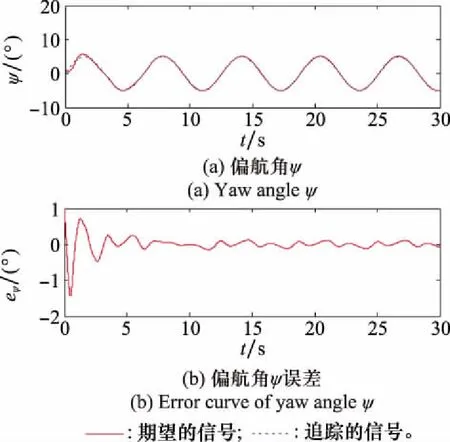
圖7 機器人偏航角及其誤差曲線圖Fig.7 Yaw angle and error curves of the robot

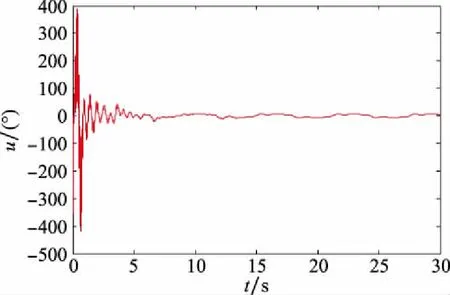
圖8 機器人#1控制輸入信號u變化曲線圖Fig.8 Control input signal variation u curve of robot#1

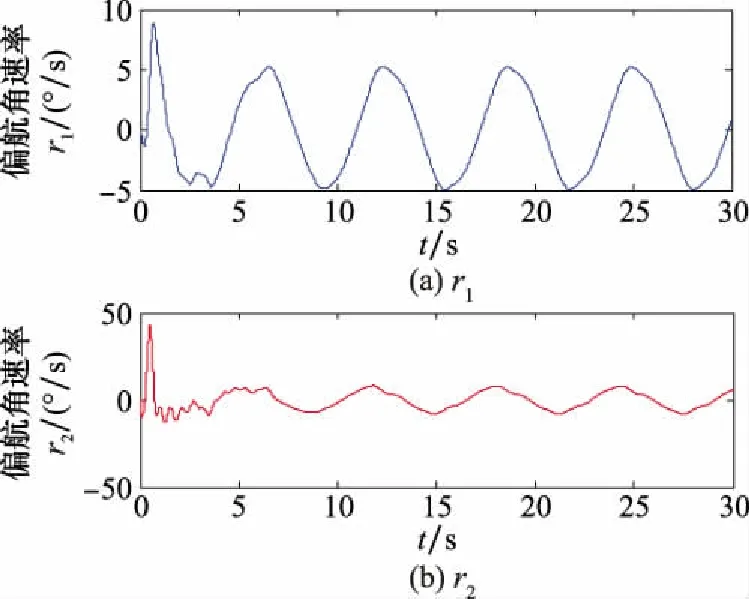
圖9 機器人#5在控制參數β1和β2的偏航角速率r1和r2的變化曲線圖Fig.9 Variation curves of the yaw rate r1 and r2 of robot #5 in control parameters β1 and β2

由仿真結果可得,所提出的控制方法,能夠提高具有執行器故障的多機器人編隊的容錯能力,同時也能夠有效實現其追蹤運動目標的目的。此外,所提出的控制方案,能夠使得機器人編隊系統在整個追蹤過程中,具有良好的容錯效果。

6 結 論

本文提出了一種基于RBFNNs的動態面協同容錯控制方法,能夠有效解決故障情形下系統參數不確定以及系統瞬態不穩定問題。首先,利用RBFNNs對系統模型中的未知光滑非線性函數進行了實時估計。其次,采用反推技術與動態面技術相結合,設計了容錯控制器,該控制器能夠在執行器發生卡死故障和部分失效故障與外部干擾作用下實現多智能體的穩定控制,并保證智能體之間的一致性。隨后,利用有限時間理論,實現了系統在預設時間內快速恢復穩定性能的需求。下一步的研究方向聚焦于以下兩個方面:帶有惡性攻擊下的多智能體系統協同一致跟蹤控制研究;基于彈性事件觸發機制下帶有惡意攻擊的多智能體編隊系統的協同容錯跟蹤控制研究。