考慮退化相關的裝備多部件系統維修決策優化模型

馬維寧, 胡起偉,*, 楊志遠

(1. 陸軍工程大學石家莊校區裝備指揮與管理系, 河北 石家莊 050003;2. 國防大學聯合作戰學院, 河北 石家莊 050003)

0 引 言

近年來,隨著大批高新裝備的研制并投入使用,部隊裝備體系發生了巨大變化,對裝備維修保障也提出了新的要求。高新裝備技術密集、結構復雜,往往是由多型號單體裝備組成的復雜系統,承擔著多樣化、復雜化的軍事任務,動用使用頻繁,任務時間要求短,保障難度大,維修費用日趨昂貴,對先進維修理論的依賴作用越來越突出。目前維修領域對單部件系統研究相對較多,而對軍事裝備系統等大部分多部件組成的復雜系統研究相對較少。復雜系統的各組成部件間存在各種關聯關系,在這種情況下,單個部件的維修決策優化結果不能直接作為整個系統的維修決策優化結果,否則將影響整個系統維修決策的科學性和合理性。因此,針對裝備多部件系統,為確保維修更加高效,系統運行更加安全可靠,考慮部件自身特點和部件間依賴關系的動態維修決策優化研究具有重要意義。

多部件系統的部件間可能存在經濟相關、結構相關和隨機相關。經濟相關包括經濟正相關和經濟負相關,如果成組維修部件的費用低于部件單獨維修的費用,則為經濟正相關;如果成組維修部件的費用高于部件單獨維修的費用,則為經濟負相關。結構相關是指當對某故障部件進行修理時必須要拆卸其他正常工作的部件。隨機相關是指部件間的故障或退化將影響其他部件的退化或壽命分布。在多部件系統維修優化問題中,研究較多的是以最小化維修費用為優化目標。如文獻[4]利用整數規劃方法建立了考慮區間費用的多部件系統預防性維修優化模型,文獻[10]在考慮經濟相關和失效相關的基礎上,建立了多部件系統折扣準則模型,得到了維修費率的最優方程,并采用聚合迭代算法獲得了最優解。在部件間隨機相關性研究方面,一種研究方法是考慮部件間故障的相關關系。如文獻[12]考慮到維修時間有限的約束條件,基于故障率分布建立了考慮預防性維修時間的動態成組維修模型。文獻[15]利用Gamma過程描述部件的退化,建立了重型卡車基于役齡的成組更換模型,該模型在決策時刻可以融合系統狀態退化信息,更新部件的故障分布,并通過滾動時間窗法不斷更新維修決策。隨機相關性的另一種研究方法是考慮部件退化的相關關系。如文獻[20]建立了考慮退化沖擊影響的可靠度模型,并使用蒙特卡羅仿真方法計算了系統可靠度。文獻[22]利用回歸的方法獲得了兩部件的交互影響關系式,通過模擬退火算法得到了低溫箱的管道視情維修優化結果,證明部件間的交互對于維修決策有著重要影響。

通過分析發現,現有的多部件系統維修優化大多只關注經濟相關,而對于隨機相關和結構相關考慮較少,忽視了系統中的負載分配以及故障傳播導致的隨機相關。另外,系統的性能狀態是隨著使用動態變化的,為此,多部件系統維修決策要能夠依據系統狀態的變化而動態調整。基于此,本文在Gamma退化過程模型基礎上,采用Frank Copula函數考慮分析系統中多部件之間的退化相關性,建立長期運行下系統可用度為目標的維修決策優化模型,采用改進人工蜂群(artificial bee colony,ABC)算法進行求解獲得系統最優維修策略,為裝備多部件系統維修決策優化提供了新的理論支持。

1 系統描述與退化過程模型

1.1 退化過程模型

令{():∈}表示系統某部件性能退化過程,()表示部件在時刻的性能退化量。若{():∈}滿足以下條件:

(1)(0)=0;

(2) 對任意時間0≤<,()-()～Ga((-),),其中Ga(·,·)表示Gamma分布。

(3)()具有獨立增量性,即對任意時間0≤<<…<,退化增量()-(),()-(),…,()-(-1)為相互獨立的隨機變量,此時,稱連續時間隨機過程{():∈}為Gamma過程,其中>0和>0分別為Gamma分布的形狀參數和尺度參數。

對于Gamma過程定義,在任意時間間隔[,]內,系統退化增量()-()服從Gamma分布,其對應的概率密度函數和累積分布函數為

(1)

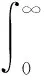
根據定義,Gamma過程為單調非減隨機過程。在式(1)基礎上,可得系統壽命的分布為

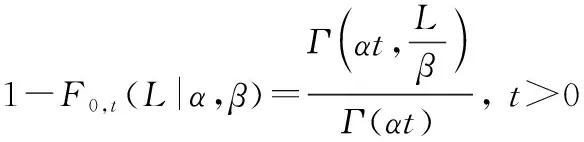
(2)

1.2 系統描述

假設某裝備系統由個不同部件串聯組成,部件性能指標隨工作時間增加不斷退化,當退化量超過特定閾值時,部件發生故障。并假設如下:

(1) 每個部件性能退化過程通過一個狀態參數即可描述；

(2) 系統各部件退化狀態只有通過檢測才能得到,且系統各部件的檢測是同時進行的,檢測結果不存在誤差；

(3) 部件故障是軟失效,即在發生故障后部件還能繼續運行,只是部件性能狀態已無法滿足使用要求,在初始時刻部件處于全新狀態。

為使建立的維修優化模型具有一般性,采用Frank Copula函數描述部件間的交互關系。Copula函數是一種常用的聯合分布工具,其提供了豐富的函數族以描述不同的相關性結構,近年來在可靠性領域有一定的應用。元Frank Copula函數可表示為

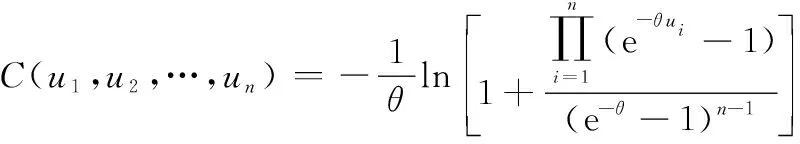
(3)

式中：表示相關性參數,當≥3時,∈(0,+∞),其值越大說明變量間的相關性越強;當→0時,Frank Copula所描述的變量關系趨于相互獨立;而當→+∞時,變量間關系趨于完全正相關。

2 裝備多部件系統維修決策建模

2.1 維修策略

對系統各部件采取機會維修、預防性維修和故障維修相結合的控制限策略,在運行過程中對各部件退化狀態進行檢測,第次檢測時刻記為,機會維修閾值記為={,…,},預防性維修閾值記為={,,…,},故障維修閾值集合記為={,,…,}。其中,≤≤。部件維修方式包括機會維修、預防性維修和故障維修。

在系統各部件維修結束后,需要根據當前系統部件退化狀態確定下次檢測時間。為提高檢測工作效益,當系統退化量較高時,應當縮短檢測時間間隔以防止系統出現故障。假設當前系統各部件退化量為(,,…,),檢測間隔期由以下檢測規劃函數確定:

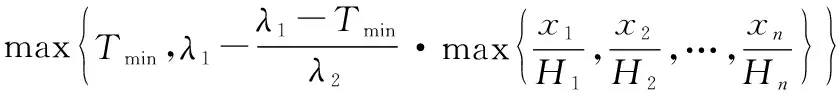
(4)

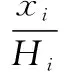
2.2 維修決策優化模型

可用度是衡量裝備系統性能好壞的重要指標之一,表示任一時刻系統處于可使用狀態的概率。本文以裝備多部件系統長期運行情況下可用度最大為優化指標,由以上維修策略可以看出,系統維修決策由變量(,,,)確定。長期運行情況下系統可用度模型表示為

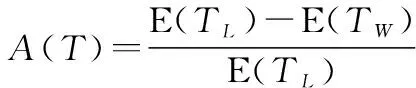
(5)

式中:E()表示系統一個壽命周期內的期望維修停機時間；E()表示系統的期望壽命周期長度。

本文研究完全維修下裝備多部件系統的維修決策優化問題。完全維修是指部件經過維修后恢復如新,通常是部件發生故障或有預防性維修需求時,采取更換的方式進行修復,此種方式在裝備維修實踐中廣泛存在。由于系統各部件的維修決策以及后續退化狀態只與當前檢測時刻的系統狀態有關,而與系統歷史狀態無關,符合Markov特性,由于經過完全維修后的部件又處于全新狀態。因此,可將任意維修決策點視為系統退化狀態的半更新點,兩個連續維修決策點之間的運行時間視為一個半更新周期,在半更新周期內,經過維修后的部件又從全新狀態(0狀態)開始退化,分析兩個連續的維修決策點之間的系統退化特征可近似代替系統的半更新循環過程。在此基礎上,分析系統退化狀態的穩態特性,進而可以得到系統期望可用度表達式:

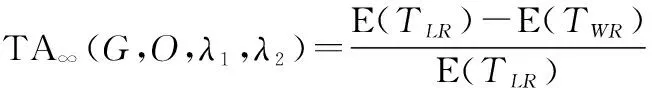
(6)

式中：E()表示一個半更新周期內的維修停機時間;E()表示半更新周期長度的期望值。

2.3 退化狀態空間劃分

在多部件系統退化建模中,采用連續狀態隨機過程模型。為建立解析模型,對連續狀態退化過程模型進行近似簡化,將連續退化過程離散化為有限個狀態空間,通過部件在不同退化狀態空間的轉移近似描述其退化過程。部件的狀態空間記為={0,1,…,,…,,},其中,0表示部件完好狀態,表示部件故障狀態。基于此,部件退化過程可用+2個離散狀態進行描述。

部件在時刻的退化量(),其與所屬退化狀態()之間的關系如下所示:

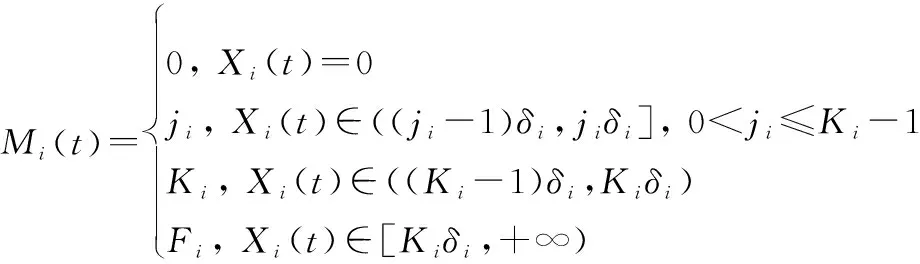
(7)

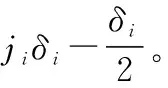
為方便分析,令表示在檢測時刻無需采取維修措施對應的系統狀態集合,表示在檢測時刻有維修活動發生對應的系統狀態集合,={(,,…,)|?,0≤()<},因此,系統狀態空間集合可表示為=∪。

2.4 系統退化穩態概率分布

為得到系統狀態穩態分布,首先需要計算系統不同退化狀態間的轉移概率。由以上狀態空間劃分方法可知,系統退化狀態由各部件狀態共同決定。因此,首先對單部件狀態轉移概率進行分析,而后計算系統狀態轉移概率,在此基礎上,可得到系統穩態概率分布。

241 單部件狀態轉移概率

在檢測間隔期[,+1]內,部件狀態轉移概率與在初始時刻的退化狀態和對應的維修方式有關。具體可劃分為以下兩種情況。

(1) 在檢測時刻,如果部件的退化量滿足()<,即不需要對其進行維修。根據Gamma過程的獨立增量特性,可得部件在時間區間[,+1]內從狀態轉移到狀態(≤≤)的概率為

,(,+1)=((+1)=|()=)=

(lb< Δ< ub)=

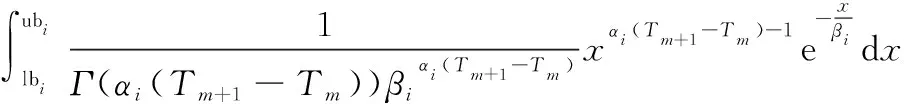
(8)

式中：Δ=(+1)-()；ub=(-+05)；lb=max{0,(--05)}。如果=,即部件在檢測間隔期內發生故障,則只需令式(8)中ub=+∞,即可得到對應的狀態轉移概率。

如果<,容易得到相應的狀態轉移概率為0,即,(,+1)=0,這是由于部件退化過程是遞增的,所以((+1)-()<0)=0。

(2) 在檢測時刻,如果系統退化量滿足()≥或=,即需要對部件進行維修。在完全維修條件下,部件經過維修后狀態恢復如新,此時,部件在時間區間[,+1]內從狀態轉移到狀態的概率可表示為

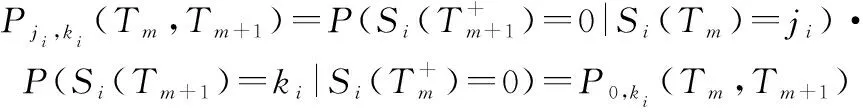
(9)

242 系統狀態轉移概率

在單部件狀態轉移概率分析基礎上,系統在時間區間[,+1]內可能發生的狀態轉移及相應概率也可分為兩種情況,分別如下。

(1) 在檢測時刻,若系統狀態滿足(,,…,)∈,則沒有發生維修作業。此時,系統由狀態(,,…,)至狀態(,,…,),?,≥的轉移概率為

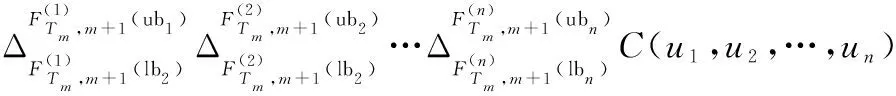
(10)

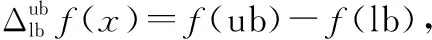
對于系統狀態(,,…,),如果滿足?,<,即至少存在一個部件的狀態轉移情況滿足<,顯然

(, ,…, ),(,,…,)(,+1)=0,原因與單部件情況相同。

(2) 在檢測時刻,若系統狀態滿足(,,…,)∈,則系統中至少有一個部件需要維修。定義表示在檢測時刻采取預防性維修和機會維修的部件集合,表示在檢測時刻采取故障維修的部件集合。基于此,在完全維修條件下,系統由狀態(,,…,)至狀態(,,…,),?,≥的轉移概率可表示為

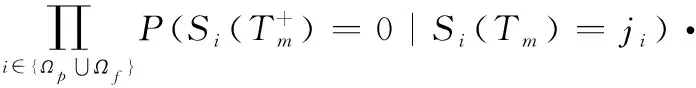
(11)

2.4.3 系統狀態轉移過程及維修方式

系統退化狀態Markov轉移過程如圖1所示。

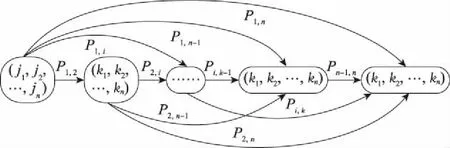
圖1 系統退化狀態轉移過程圖Fig.1 Transition process diagram of system degradation state

系統由狀態(,,…,)退化至狀態(,,…,),若?,()<,則不采取任何維修方式,只完成系統檢查工作;若某部件退化量滿足≤()<,則對部件進行預防性維修;若在檢測時刻系統有維修活動發生,即?,有()≥,則對于滿足≤()<的所有部件(≠)進行機會維修。否則,不進行機會維修;若某部件退化量滿足()≥,則對部件進行故障維修。

244 系統穩態概率分布計算

在以上系統狀態轉移概率分析基礎上,由Markov穩態分布特性可知系統穩態概率分布滿足以下方程組:

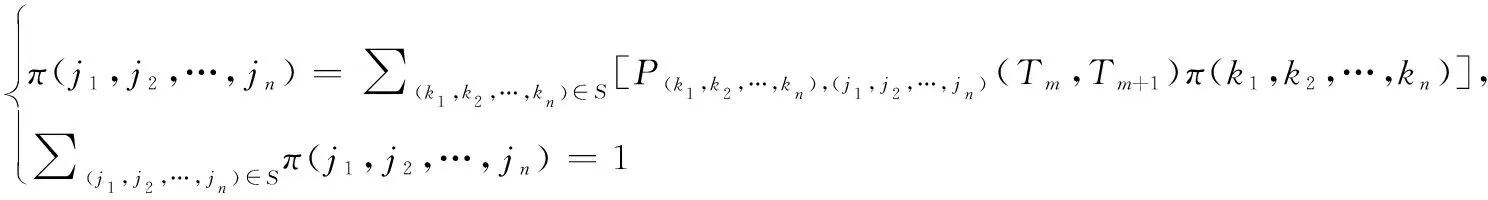
(12)

其中,(,,…,)表示系統處于狀態(,,…,)的穩態概率。

2.5 系統期望可用度模型

基于上述系統穩態概率分布,利用系統半更新過程特性,可得到長期運行條件下的系統期望可用度。記系統每次檢測時間為,部件的機會維修時間為,,預防性維修時間為,,故障更換時間為,,維修準備時間為,。一般來說,,>,。由于機會維修實質屬于預防性維修,因此本文認為機會維修所需時間,與預防性維修所需時間,相等。由式(6)維修決策優化模型可知,要計算系統期望可用度,需分別計算系統維修停機時間和系統半更新周期長度。

(1) 系統維修停機時間

當系統在檢測時刻狀態為(,,…,)時,令(, ,…, )表示系統在該半更新周期內的期望維修停機時間。

根據(,,…,)取值不同,維修停機時間(, ,…, )可表示為

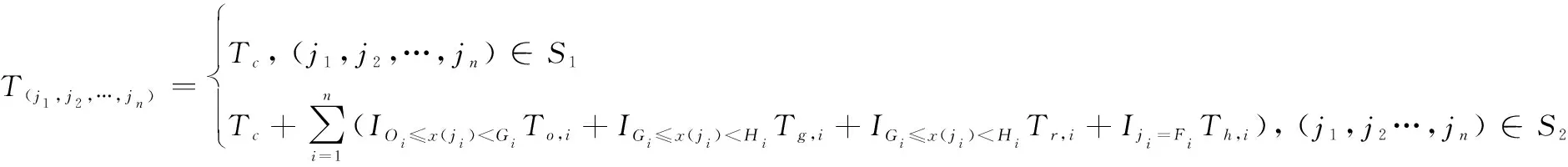
(13)

式中：為示性函數。

結合系統穩態概率分布(,,…,),可得一個半更新周期內系統期望維修停機時間為

E()=∑(, ,…, )∈(, ,…, )π(,,…,)

(14)

(2) 半更新周期長度

半更新周期長度即為檢測間隔期,系統檢測間隔期由檢測時刻的退化狀態及相應維修方式決定,令(, ,…, )表示系統當前狀態(,,…,)對應的半更新周期長度。根據(,,…,)取值不同,半更新周期長度(, ,…, )取值可分為以下兩種情況。

當系統狀態(,,…,)∈時,根據檢測規劃函數式和退化空間劃分方法,半更新周期長度可表示為

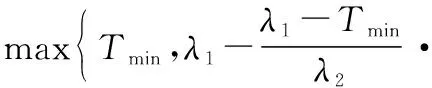
(15)

當系統狀態(,,…,)∈時,半更新周期長度可表示為

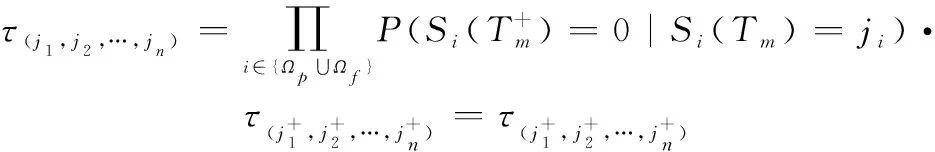
(16)

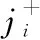
結合系統穩態概率分布(,,…,),可得系統期望半更新周期長度為

E()=∑(, ,…, )∈(, ,…, )(,,…,)

(17)

綜合上述系統各狀態對應維修停機時間和半更新周期長度,以及系統狀態穩態概率分布,在維修決策變量(,,,)確定時,系統期望可用度可表示為

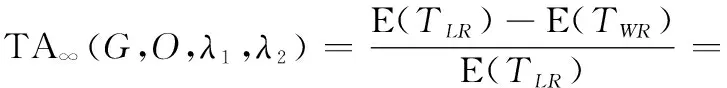
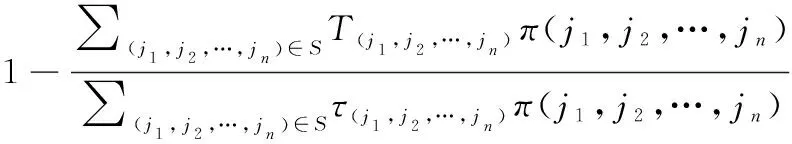
(18)

2.6 維修決策優化模型

在期望可用度模型基礎上,以系統期望可用度最大為目標,對維修決策參數(,,,)進行優化。考慮決策變量的約束條件,對應的系統維修決策優化模型如下:

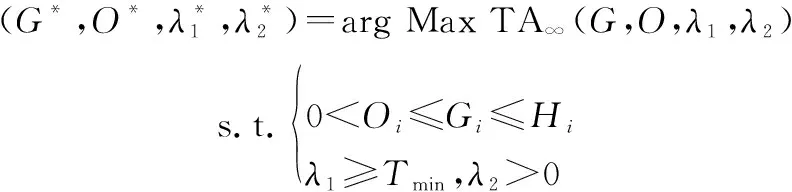
(19)

其中,第一個約束條件限制了機會維修閾值和預防性維修閾值的取值范圍。

2.7 基于改進ABC算法的模型求解

上述系統維修決策優化模型中,決策變量對目標函數的影響是非線性、不可微的,且模型決策變化較多,當系統存在個部件時,模型有2+2個決策變量,難以用傳統方法得到解析解。當前,智能優化算法已廣泛應用于復雜系統維修決策優化,如遺傳算法、模擬退火算法、粒子群算法等,雖然這些算法可以得到所建模型的近似最優解,但因為決策變量較多,仍存在全局搜索能力不足、易陷入局部最優等問題。ABC算法是由Karaboga基于蜂群搜索蜜源行為提出的一種啟發式群體智能優化算法。相比之下,ABC算法在尋優過程中兼顧局部搜索和全局搜索,控制參數少、易于實現,在非線性函數優化求解方面具有良好的性能。基于此,本文采用ABC算法進行求解。同時,為提高搜索效率,對ABC算法進行改進。對于決策變量和來說,,-2<≤,+2和,-2<≤,+2,與=,和=,對應的系統期望可用度TA是相同的。因此,以將決策變量和的搜索空間轉化為,,,∈{0,1,2,…,},,<,,以上處理方法在很大程度上減少了算法搜索空間。

基于以上分析,對于決策變量預防性維修閾值和機會維修閾值來說,采蜜蜂階段和觀察蜂階段的搜索方程分別為

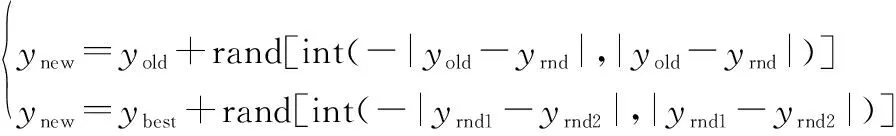
(20)

式中：和分別為蜜源新位置和初始位置；為當前種群最優位置；、和分別為隨機選擇的其他蜜源位置；rand[int(,)]表示區間[,]內的隨機整數；決策變量和,仍采用原來的搜索方程產生備選解。

3 算例分析

該算例考慮某系統由3個存在退化相關的部件組成,為便于分析,假設部件1和部件3相同,每個部件的退化特征均從0狀態開始,且服從增量非負、穩定、隨機獨立的Gamma分布,設定3個部件的故障維修閾值分別為4 mm、5 mm和4 mm,Gamma退化過程的形狀參數分別為(,,)=(1,2,1),尺度參數分別為(,,)=(23,12,23),系統檢測時間為0.01 h,維修準備時間為0.1 h,狀態數量參數均為10,因此,離散狀態對應的退化量區間長度(,,)=(04,05,04)。選用Frank Copula函數描述系統中3個部件退化間的相關關系。三元Frank Copula函數可表示為

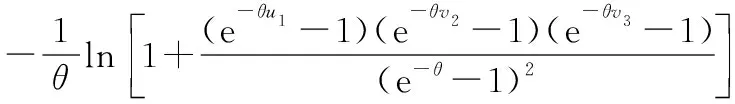
(21)

在本算例中,設定退化相關性參數的值為5。

3.1 系統穩態分布計算

由上述維修決策優化模型知,系統穩態分布與維修決策變量值相關,即在不同的維修決策變量取值(,,,)下,系統穩態分布不同,系統期望可用度也會相應隨之變化。以決策變量值(,,,,,,,)=(28,25,28,16,15,16)為例,分析系統穩態概率分布特征,如圖2所示。

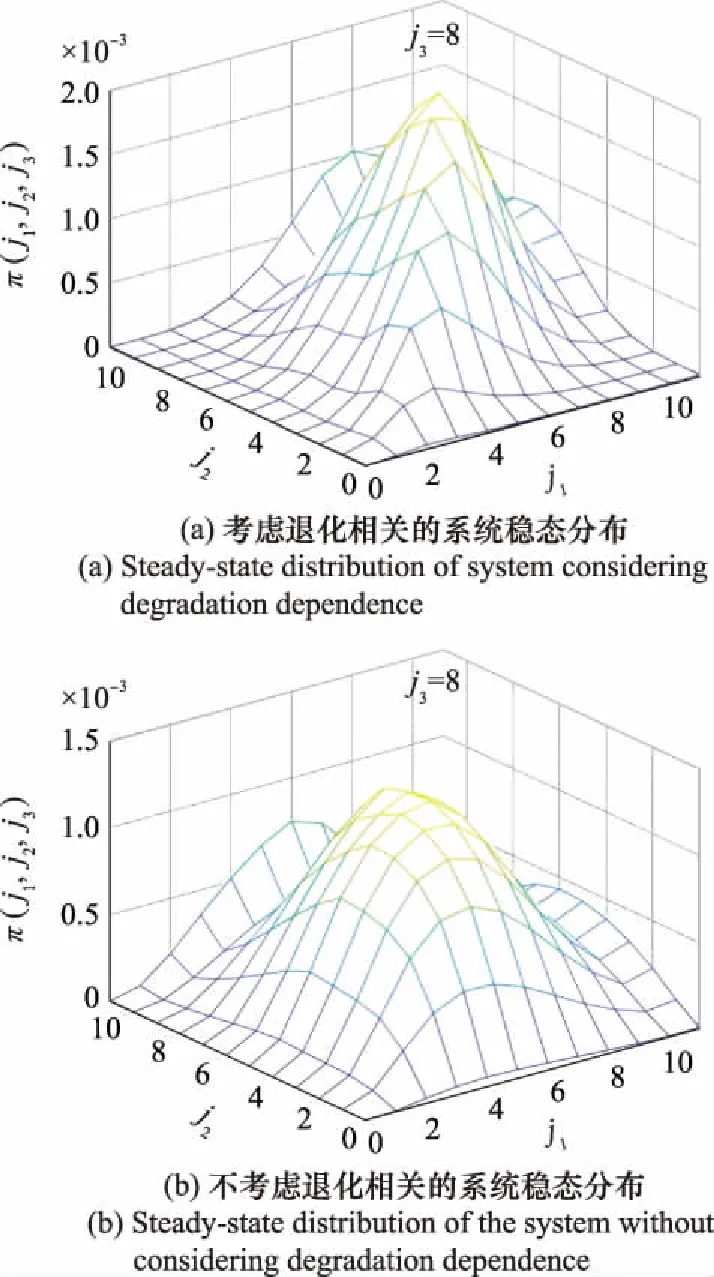
圖2 系統穩態分布Fig.2 Steady-state distribution of system

圖2分別給出了在部件3狀態=8時,考慮退化相關性和獨立條件下其余兩個部件的穩態分布。由圖2對比可以看出,退化相關性對系統穩態分布特征有明顯影響,相對于部件相互獨立的情況,在系統長期運行條件下,考慮退化相關性時系統退化狀態的分布更為集中。同時,由于系統中3個部件不完全相同,且存在一定的相關關系,因此對應穩態分布曲面是非對稱的。

3.2 維修策略優化

(1) 檢測間隔期參數對優化目標的影響

分析檢測間隔期參數(,)變化對系統期望可用度TA的影響。首先,固定預防性維修閾值和機會維修閾值,當預防性維修閾值分別為(,,)=(28,25,28),機會維修閾值分別為(,,)=(2,15,2)時,系統半更新周期內期望可用度隨檢測間隔期參數(,)的變化趨勢如圖3所示。其中,的取值范圍為[1～5],的取值范圍為[02～2]。

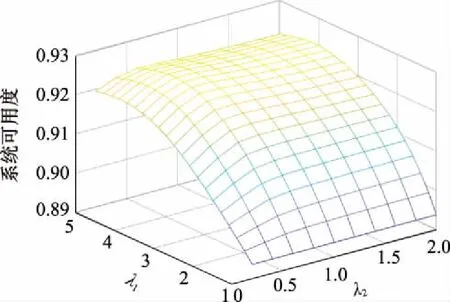
圖3 檢測間隔期參數對系統可用度的影響Fig.3 Influence of detection interval parameter on system availability

由圖3可以看出,當固定預防性維修閾值和機會維修閾值時,隨著(,)的增大,TA先增大后減小。這是由于當檢測間隔期較小時,頻繁的檢測會增加維修停機時間,系統運行時間相對減少,因而TA較小。隨著(,)的增大,檢測間隔期逐漸增大,系統運行時間相應延長,因而TA隨之增大。當檢測間隔期較大時,會增加系統故障概率,而故障后維修時間一般較長,又會使得TA呈現下降趨勢。總體來說,存在最優的(,)值使得TA達到最大。

(2) 預防性維修閾值和機會維修閾值對優化目標的影響

類似地,固定參數(,,)=(04,1,04),(,)=(3,08),分析預防性維修閾值的變化對期望可用度TA的影響,TA隨預防性維修閾值的變化趨勢如圖4(a)所示。之后,固定參數(,,)=(32,4,32),(,)=(3,08)分析機會維修閾值變化對系統期望可用度TA的影響,TA隨機會維修閾值的變化趨勢如圖4(b)所示。

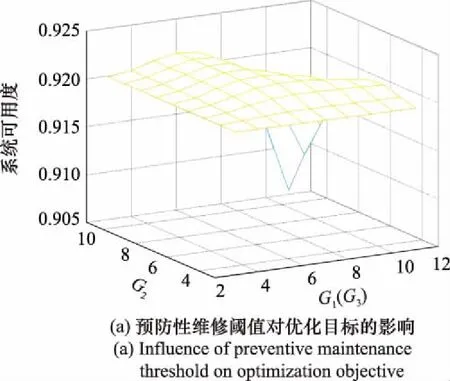
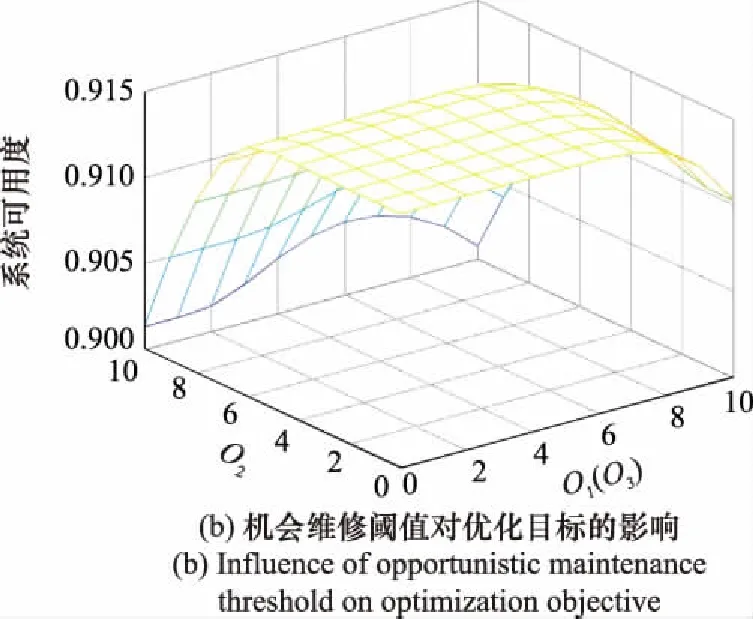
圖4 維修閾值對優化目標的影響Fig.4 Influence of maintenance threshold on optimization objective

由圖4可以看出,隨著預防性維修閾值或機會維修閾值的增大,系統期望可用度TA呈現先增大后減小的趨勢。這是因為當或較小時,半更新周期內對各部件預防性維修和機會維修的概率較大,不能充分利用各部件的使用壽命,增加了系統維修停機時間;當或逐漸增大時,預防性維修和機會維修區域縮小,各部件預防性維修和機會維修概率隨之降低,TA逐漸增大;當或較大時,系統各部件發生故障的概率較高,受故障后維修時間較長的影響,導致TA相應減小。總體來說,存在最優維修閾值和使得系統期望可用度TA最大。

(3) 基于ABC算法的維修策略優化

設置ABC算法的優化參數為種群數量10,更新次數20,最大迭代次數100,ABC算法的一次優化迭代過程如圖5所示。

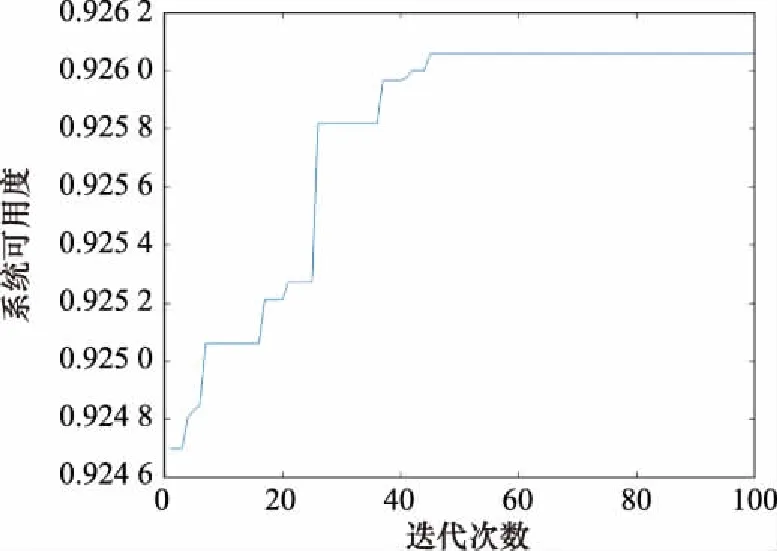
圖5 ABC算法的一次優化過程Fig.5 An optimization process of ABC algorithm

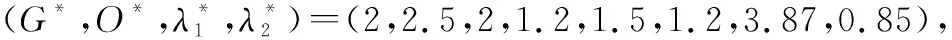
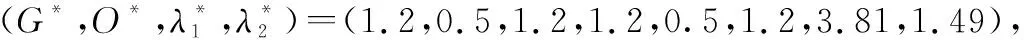
3.3 靈敏度分析

針對本文所建立的維修決策優化模型,影響系統可用度的3個重要因素分別是維修停機時間、Copula函數中退化相關性參數和各部件狀態數量參數,在此分析這3個參數對優化結果的影響。

3.3.1 維修準備時間

維修準備時間直接影響系統可用度的大小。在其余參數設置不變的條件下,分析維修停機時間對優化目標的影響,如圖1所示。

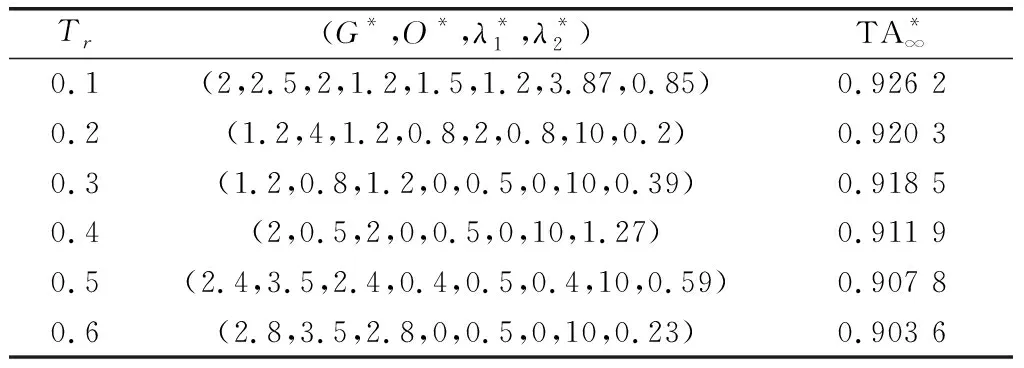
表1 維修準備時間對維修優化結果的影響Table 1 Influence of maintenance preparation time on maintenance optimization result

由表1可知,隨著維修準備時間的增大,系統運行時間相應減小,系統可用度呈逐漸下降趨勢,特別是當維修準備時間較長時,會出現部件機會維修閾值為0的情況,這表明在檢測時刻就要對相應部件進行更換,這也說明利用維修停機時間對盡可能多的部件同時安排維修工作的重要意義。

3.3.2 退化相關性參數

本文考慮退化相關條件下多部件系統的維修決策優化問題,因此需要分析退化相關性參數θ對優化結果的影響。在系統退化過程和其他參數不變的情況下,不同θ值對應的最優維修策略如表2所示。

表2 退化相關性參數對維修優化結果的影響Table 2 Influence of degradation dependence parameter on maintenance optimization result

由表2可知,隨著退化相關性參數的增大(即系統部件間退化相關性的增強),系統最優視情維修策略也會相應發生變化。注意到當值較大時(>5),部件維修閾值會相應降低,這是由于為確保系統長期穩定可靠運行,維修閾值的降低可以提前對部件進行預防性維修和機會維修,從而提高了系統可用度。

同時,隨著退化相關性參數的增大,系統期望可用度也隨之提高,這是由于隨著部件間退化相關性的增強,可以利用維修停機時間對相關部件進行同時維修,減少了額外的維修停機時間,從而提高了系統的可用度。

333 狀態數量參數

本文在推導系統穩態概率分布時,采用離散化系統狀態近似代替連續狀態退化過程,各部件狀態數量參數會直接影響系統期望可用度的計算精度,因此,有必要分析狀態數量參數對優化結果的影響,如表3所示。

表3 狀態數量參數對維修優化結果的影響Table 3 Influence of state amount parameter on maintenance optimization result

由表3可知,在不同的狀態數量參數下,系統有著不同的最優預防性維修閾值和機會維修閾值。狀態數量參數越小,系統可用度越大。隨著狀態數量參數的增大,系統期望可用度逐漸降低。這是由于狀態數量參數的變化,引起系統預防性維修閾值和機會維修閾值的變化,系統維修停機時間逐漸增大,從而導致系統可用度降低。

4 結 論

本文考慮裝備多部件系統任務特性的實際需求,以長期運行下系統可用度為目標建立了維修決策優化模型,采用Gamma過程描述系統退化過程,采用Frank Copula函數描述系統各部件間相關關系,并利用改進ABC算法進行了求解,獲得了系統最優檢測間隔期和維修閾值,通過算例驗證了模型的有效性和可實施性,為裝備多部件系統預防性維修策略的實施提供了理論支持。