融合功率分配策略的NGSO-GSO頻率干擾計算方法研究

董蘇惠, 潘 冀, 姚秀娟, 高 翔, 閆 毅, 智 佳

(1. 中國科學院國家空間科學中心, 北京 100190; 2. 中國科學院大學, 北京 100049;3. 國家無線電監測中心, 北京 100037)

0 引 言

由于低軌寬帶互聯網星座系統可以實現全球通信的無縫覆蓋,且具有頻譜利用率高、通信時延短、通信容量大的特點,成為近幾年來衛星通信領域的發展熱點,典型如StarLink星座系統、OneWeb的星座系統、Telesat的星座系統等[1-3]。衛星星座系統的大量部署使空間頻譜和軌道資源異常緊張,特別是大規模非對地靜止軌道(none geostationary satellite orbit, NGSO)衛星星座系統對地球靜止軌道(geostationary satellite orbit, GSO)衛星系統的頻率重疊問題嚴重,迫切需要探索有效、實用的干擾分析方法,為它們之間的頻率兼容性共存提供技術支撐。

國內外針對NGSO與GSO系統間的兼容性分析已經開展了很多研究工作,具有較高的指導意義[4-6],其中文獻[4]主要研究了緩解NGSO系統對GSO系統的共線干擾,文獻[7-11]主要通過空間特征中的空間隔離來避免干擾,如提出地球站的隔離角和劃分干擾規避區域,文獻[12]則通過劃分信道的方式來實現頻譜的復用,文獻[13]通過基于距離和業務流量認知的功率控制方法抑制了NGSO系統對GSO系統的干擾,文獻[14]研究了頻率復用因子為7的多波束GSO和NGSO衛星共存的認知衛星系統,所提波束功率控制方法在保證GSO用戶服務質量約束下,提高了NGSO衛星的吞吐量,文獻[15]針對GSO和NGSO的雙星系統提出一種基于頻率動態分配的頻譜共享方法。但由于技術發展和實驗條件的限制,融合功率分配策略的NGSO-GSO系統間的頻率干擾分析方法的研究較少。

本文在考慮了GSO系統與NGSO星座的空間特征、波束業務特征及信道特征的基礎上,針對GSO衛星系統和NGSO星座系統分別提出了對應的融合了帶寬和波束特征的功率分配策略。并在下行及上行干擾分析場景中構建了相應分配策略的目標函數和約束條件,在滿足空間隔離條件下,分析比較了不同分配策略對NGSO-GSO間干擾噪聲比I/N的影響效果,所提方法對緩解NGSO星座對GSO系統的干擾具有一定的作用,為NGSO-GSO間的頻率兼容分析提供一種參考。

1 基于空間特征的功率分配方法

1.1 鏈路分離角

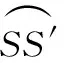
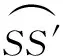
(1)

(2)

則鏈路分離角α可由下式計算得到：

(3)

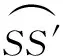
1.2 基于鏈路分離角的干擾場景構建

如圖2和圖3所示,GSO衛星由于南北偏移θ角度的軌道攝動,會產生GSO帶。在圖2下行場景中,當NGSO星座中的衛星與GSO衛星、GSO地球站三者共線時,GSO地球站接收到NGSO衛星的下行干擾達到最大值[4-5],此時NGSO衛星對GSO衛星產生的干擾稱之為最壞干擾。在圖3上行鏈路分析場景中,NGSO衛星波束覆蓋范圍內的多個地球站的上行天線波束會對GSO衛星產生集總干擾。

當NGSO地球站的鏈路分離角α小于某一閾值αth時,NGSO星座系統需要采取波束關閉或切換或降低發射功率的操作,以降低NGSO星座系統對GSO系統的同道干擾[10]。

2 上下行通信鏈路建立條件

在同向上行或下行鏈路干擾分析場景中,由于NGSO星座系統的鏈路復雜性,會有多條來自NGSO系統的干擾鏈路對GSO系統的接收機造成干擾,因此主要考慮NGSO星座系統對GSO衛星系統造成的集總干擾。那么GSO系統的接收機接收的集總干擾噪聲比(interference to noise ratio, INR) ∑I/N表示為

(4)

式中:Numngso為干擾系統的發射機總數;Mi為干擾系統中第i個發射機的干擾鏈路建立的總數;N為受擾系統接收機的等效噪聲功率;(I/N)i, j為干擾系統第i個發射機建立的第j條干擾鏈路上的干擾噪聲比。其中,(I/N)ij可由下式[4]計算得到:

(5)

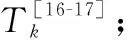
(6)

式中:gtx,max為該衛星系統天線最大發射增益;gre,max為該衛星系統天線最大接收增益;lk為第k個波束建立的通信鏈路的損耗,具體為

(7)

式中:fk為第k個波束的中心通信頻率,單位為Hz;ds→es為星地鏈路的距離,m;Ar,k為星地鏈路中降雨引起的衰減值,單位為dB;Ac,k為星地鏈路中云霧引起的衰減值,單位為dB[18]。

3 功率分配目標函數構建方法及效果分析

為便于分析,被干擾GSO衛星上行通信鏈路選取CHNNEWSAT-G1-118E和101.5E衛星在ITU登記的上行KAUWB波束和空口參數;下行通信鏈路選取CHNNEWSAT-G1-118E衛星的下行KADWB波束和空口參數[19],如表1所示。干擾NGSO星座系統則參考OneWeb星座的軌道構型,即軌道高度為1 200 km的18個軌道平面共計720顆衛星,波束及空口參數依據其在ITU登記的上行GRA波束和下行GTA波束信息[20],頻率范圍選擇與GSO衛星頻率重疊的部分,如表2所示。

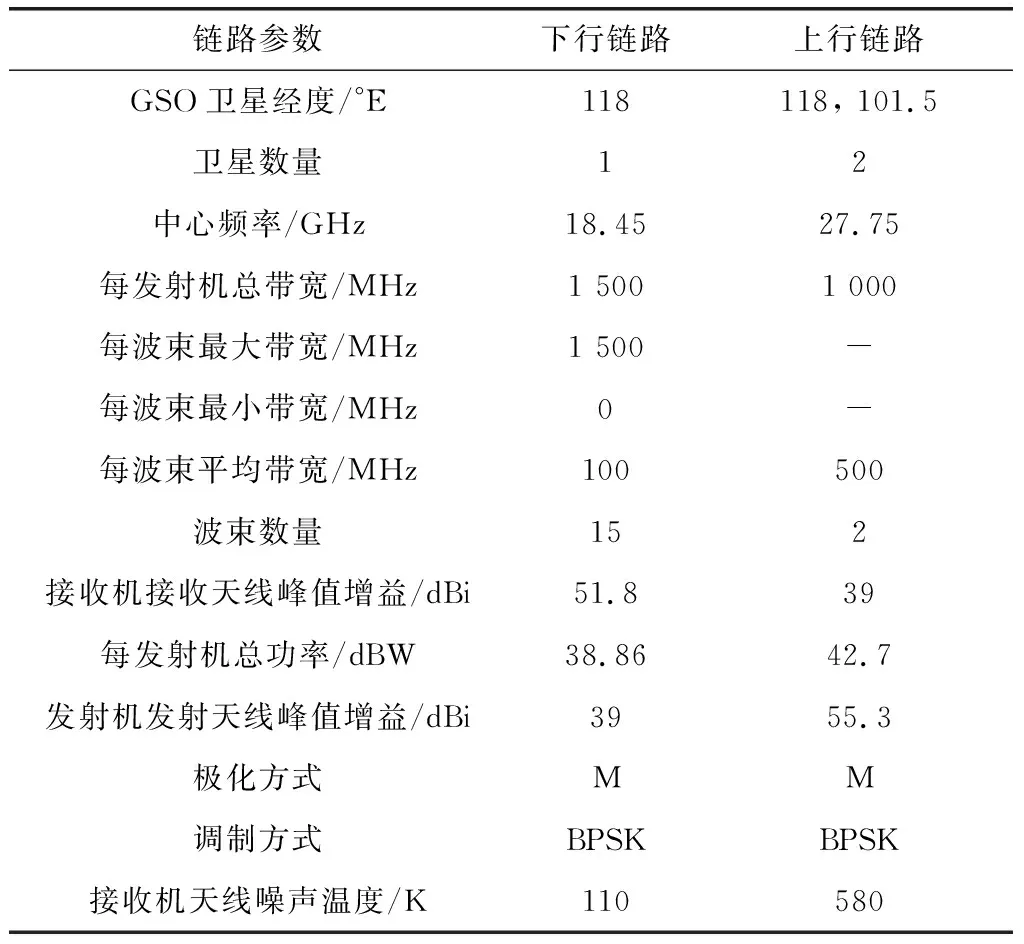
表1 GSO系統上行及下行鏈路軌道、波束及空口參數Table 1 Orbit, beam and air interface parameters of GSO systems for uplink and downlink

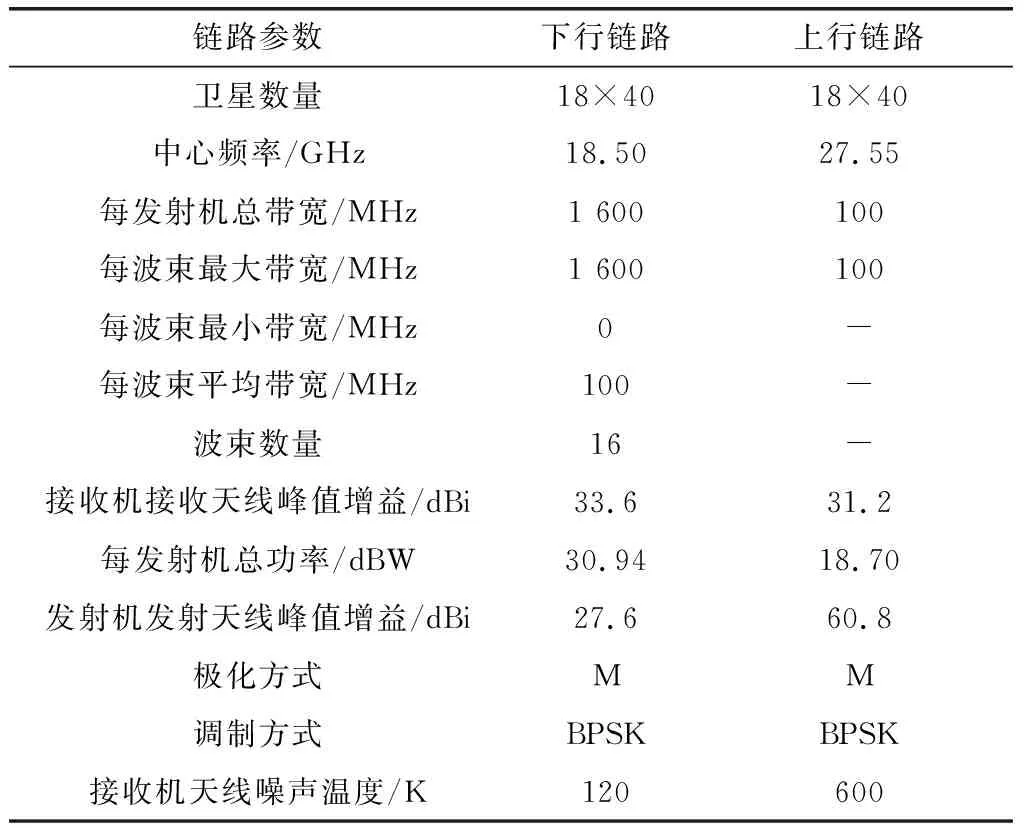
表2 NGSO系統上行及下行鏈路波束及空口參數Table 2 Beam and air interface parameters of NGSO systems for uplink and downlink

3.1 下行鏈路目標函數構建方法

本節對下行通信鏈路功率分配方法的研究主要基于系統信道容量的公平性分配原則。在對帶寬和功率資源分配時,結合GSO衛星系統和NGSO星座系統各自建鏈的特點和復雜性,考慮下行鏈路不同波束覆蓋區域的業務需求量的差異,針對性設計相匹配的功率分配策略。

3.1.1 GSO衛星系統下行鏈路目標函數構建

受擾多波束衛星系統第k個波束建立的通信鏈路的信道容量Rk為

(8)

為追求系統資源分配的公平性,結合GSO衛星系統通信鏈路拓撲結構的相對固定性,可將多波束GSO衛星系統業務需求量Tk和鏈路的信道容量Rk的偏差作為待優化的目標函數,具體形式為

(9)

本節涉及的不同波束業務需求量與波束覆蓋的中心區域的人口流量成正比[17],基于式(9)所示的目標函數,可以采用帶寬和功率的聯合分配(joint bandwidth and power allocation, JBPA)策略[21],對應的約束條件[21]為

(10)

此外,如果考慮多波束業務的實時性,還需要考慮波束的時延特征。多波束GSO衛星系統第k個波束的平均最大容許時延限制Dk[22-23]為

(11)

式中:ek為第k個波束建立的通信鏈路的誤包率(packet error rate, PER)。

在式(9)的基礎上,將GSO衛星系統的多波束容許時延限制Dk作為非線性約束條件,采用考慮時延的帶寬和功率聯合分配(time delayed bandwidth and power allocation, TD-BPA)策略[22-23]時,對應的約束條件如下:

(12)

本文將這種融合干擾、業務需求量及鏈路建立條件的帶寬和功率分配策略稱之為多特征融合的功率分配(multi-feature fused bandwidth and power allocation, MFF-BPA)策略,采用該策略構建的目標函數為

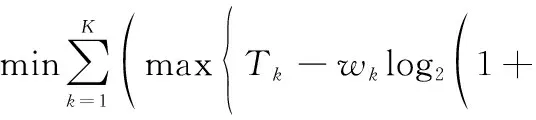
(13)

則MFF-BPA策略的約束條件為

(14)

上述構建的非線性規劃問題可以通過采用拉格朗日對偶理論的次梯度求解法來求解[21,23-25],該法可以尋找到優化問題的最優解和近似解,但算法求解的收斂速度較慢。本節在功率受限的條件下,在點波束所在區域業務需求高于容量環境下進行資源分配,依據式(13)和式(14)構建的拉格朗日函數J(·)為

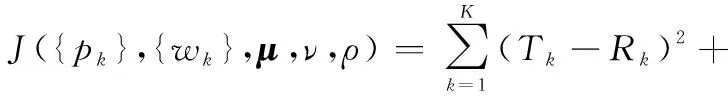
(15)

(16)

(17)

J(·)對pk和wk的偏導函數為

(18)

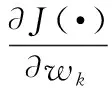
(19)

式中:

(20)

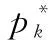
(21)

式中:step為迭代次數,當Δpk<ε1和Δwk<ε2時停止迭代。并利用梯度法更新μk,ν和ρ的值,可以得到

(22)

式中:[·]+=max(·,0);Δstep為迭代步長。根據式(15)～式(22),MFF-BPA策略求解算法如算法1所示。

下述求解目標函數問題也可以轉換為求解凸優化問題,參考算法1求解算法,進而實現求解目標函數。

算法 1 MFF-BPA策略求解算法輸入:表1的波束及空口參數,ε1,ε2輸出: {pk}和{wk}最優分配p*k,w*k1: initialize: p0k, w0k;∥初始化各波束分配的功率和帶寬值2: initialize: μ0k,υ0,ρ0;∥初始化拉格朗日因子3: repeat∥開始迭代4: calculate pstep+1k,wstep+1k;∥利用牛頓迭代法5: ifΔpk<ε1&&Δwk<ε2, then6: break7: else8: update μstep+1k,νstep+1,ρstep+1;∥更新拉格朗日因子9: update pstep+1k,wstep+1k;10: end if11: p*k←pstep+1k;12: w*k←wstep+1k;13: return p*k,w*k

3.1.2 NGSO星座下行鏈路目標函數構建

NGSO星座系統具有星座規模巨大和鏈路復雜的特點,通信鏈路的建立和斷開也具有高動態性,因而,通信資源的分配具有較高的復雜性。由于業務類型和用戶數量眾多,系統容量是星座系統建設及運行中需要考慮的關鍵因素之一。故而,本文主要將多波束NGSO星座系統容量的最大化作為待優化的目標函數,具體形式為

(23)

式中:L為每個衛星發射機發射的波束個數。

參考第3.1.1節GSO衛星系統波束的功率分配策略,對NGSO星座系統有限的功率和帶寬資源進行分配,基于式(23)所示的目標函數,采用JBPA策略對應的約束條件為

(24)

相似地,依據第2節提出的建鏈條件,忽略小于鏈路建立閾值[C/N]th的次要載波,可以降低頻率干擾仿真中的運算量。該策略稱之為融合干擾及建鏈條件的帶寬和功率分配(interference and link fused bandwidth and power allocation, ILF-BPA)策略,則該策略的目標函數為

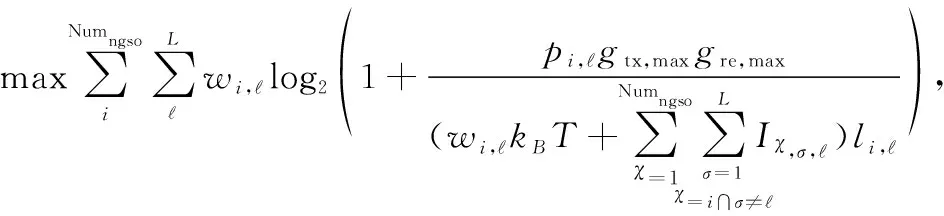
(25)

為了避免式(25)中信道容量最大化的分配策略所產生的功率分配失衡現象,在ILF-BPA策略的約束條件中對這種現象進行了補償和改善,其形式為

(26)

3.2 上行鏈路目標函數構建方法

上行鏈路的功率分配主要考慮如何緩解上行鏈路信道衰落帶來的影響,以保證鏈路的通信質量。

3.2.1 GSO衛星系統上行鏈路目標函數構建

參考第3.1節下行場景,假設上行多波束GSO衛星系統的地球站共有Numgso個發射機,每個發射機有K個波束為視距內多個不同的GSO衛星提供服務,信道容量矩陣R為

?k∈K;?ξ∈Numgso

(27)

式中:Rξ,k為地球站的第ξ個發射機的第k個波束的信道容量。

GSO衛星上行鏈路的ILF-BPA策略主要基于最小容量最大化的方法[26-27],則對地球站的第ξ個發射機構建的目標函數和約束分別為

(28)

式中:

(29)

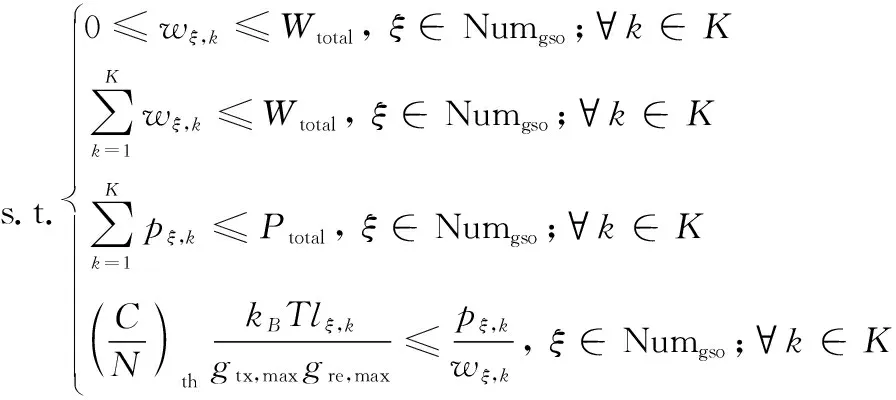
(30)

如式(28)～式(30)所示,該分配策略考慮到了不同信道條件的差異,將最小容量的最大值作為目標函數,并考慮將建鏈條件作為約束條件之一,保證了信道的可靠通信。

3.2.2 NGSO星座系統上行鏈路目標函數構建

與GSO衛星系統上行場景相似,針對NGSO星座的ILF-BPA策略也可以采取基于最小容量最大化的方法[26-27],其中Numngso為NGSO星座系統中上行鏈路干擾地球站的發射機總數,每個發射機有L個波束為視距內多個不同的NGSO衛星提供服務,則NGSO系統中地球站的第i個發射機構建的目標函數和約束為

(31)

式中:

?∈L；?i∈Numngso；?σ∈L；?χ∈Numngso

(32)

(33)

3.3 下行及上行鏈路構建的目標函數對功率密度的影響研究

3.3.1 下行鏈路計算結果分析

參考表1中下行鏈路波束及空口參數,GSO衛星下行15個波束均勻覆蓋緯度15°N～50°N范圍以及經度85°E～130°E范圍,并在波束中心布設下行鏈路的地球站,則可計算出GSO衛星系統各下行波束業務需求量Tk和鏈路損耗lk,如圖4所示。

依據式(9)、式(10)、式(12)～式(14),采用帶寬和功率均勻分配(uniform bandwidth and power allocation, UBPA)、JBPA、TD-BPA及MFF-BPA這4種分配策略,計算得到的GSO衛星系統各波束的功率密度pk/wk值,其中該GSO衛星下行的[C/N]th值為14 dB[19],各波束由于時延引起的最小業務需求量為Tk的20%[23],∑kpk和∑kwk與Ptotal,Wtotal的偏差不超過10-8,如圖5所示。

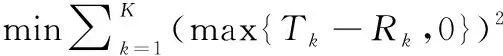
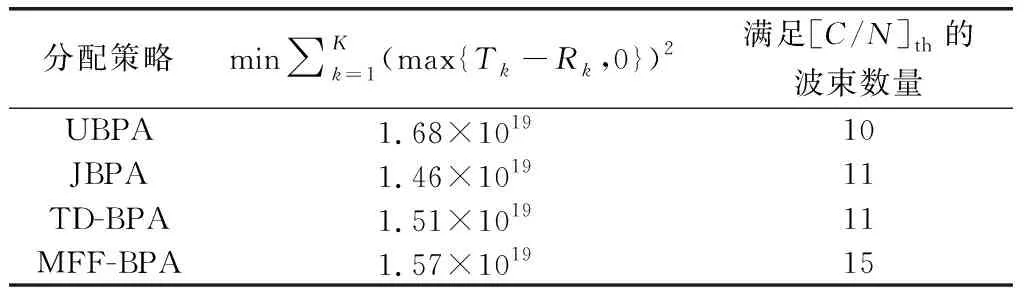
表3 不同分配策略下的GSO衛星下行鏈路波束目標函數值Table 3 Objective function values calculated by different allocation strategies of the GSO downlink beam

以距表1中GSO衛星最近的一顆OneWeb星座系統的衛星為例,參考表2的下行鏈路波束及空口參數,該星上發射波束的鏈路損耗li,以及采用不同分配策略計算得到的該星上各波束的功率密度pi,/wi,值如圖6所示, 其中OneWeb衛星在ITU登記的[C/N]th值為10 dB[20],∑pi,和∑wi,與Ptotal,Wtotal的偏差不超過10-8。

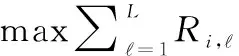
表4 NGSO下行鏈路波束3種分配策略下的目標函數值Table 4 Objective function values obtained by three alocation strategies of the NGSO downlink beam

圖6中JBPA策略分配得到的序號為{1,5,6,8,9,13,14,15,16}的波束無法滿足該星在ITU登記的C/N建鏈的最小值;UBPA策略得到的序號為{1,6,8,9,13,14,15,16}的波束無法滿足該星在ITU登記的C/N建鏈的最小值。

3.3.2 上行鏈路計算結果分析

依據表1中GSO衛星上行鏈路波束及空口參數,假設有多個地球站為視距(line of sight, LOS)內的軌道位置為118°E和101.5°E的GSO衛星提供服務,每個地球站的發射機有2個波束,采用星歷引導分別跟蹤這2顆衛星。假設地球站位于中國的55個主要熱點城市,分布情況如圖7所示。

依據式(28)～式(30),采用不同分配策略計算得到的每個地球站發射機各個波束的功率密度pξ,k/wξ,k分配情況如圖8所示,其中[C/N]th值為14 dB[19],∑kpξ,k和∑kwξ,k與Ptotal,Wtotal的偏差不超過10-8。

圖8中,對于JBPA策略,序號為{34,50}的地球站指向118°E GSO的上行波束和序號為{10,19,45}的地球站指向101.5°E GSO的上行波束低于[C/N]th;對于UBPA策略,序號為{42,45}的地球站指向101.5°E GSO的上行波束低于[C/N]th。圖9為圖8中按照這3種分配策略計算得到的上行鏈路目標函數最小信道容量Rξ,k的最大值的對比曲線。

考慮到上行鏈路地球站位置的分布范圍,該緯度范圍的LOS內的平均OneWeb衛星數目不超過2顆(考慮到FCC文件中報告的最小仰角)[28],其上行鏈路的功率分配可簡單化處理,本文不再贅述。

4 融合功率分配策略對NGSO-GSO間的I/N值評估的影響分析

參考表1和表2的上下行波束空口參數和第3節的方法,對NGSO星座系統與GSO系統的INRI/N進行概率統計計算。

對于下行鏈路,在受擾GSO衛星系統分別采用UBPA、JBPA和MFF-BPA策略,干擾NGSO星座系統分別采用UBPA、JBPA和ILF-BPA策略條件下,研究INRI/N的時間累積百分比的變化特性曲線,如圖10所示;對于上行鏈路,主要研究受擾GSO衛星系統采用UBPA、JBPA和ILF-BPA策略下的INRI/N的時間累積百分比的變化特性曲線,如圖11所示。其中αth=75°,調制方式為BPSK,時間步長為10 s,時長為1 d,NGSO系統星上天線方向圖參考建議書ITU-R S.1528[29],GSO星上天線參考建議書ITU-R S.672-4[30],地球站方向圖參考建議書ITU-R S.465-6[31]。

圖10和圖11中的各曲線的INRI/N超過-12.2 dB限值百分比的結果情況如表5所示。

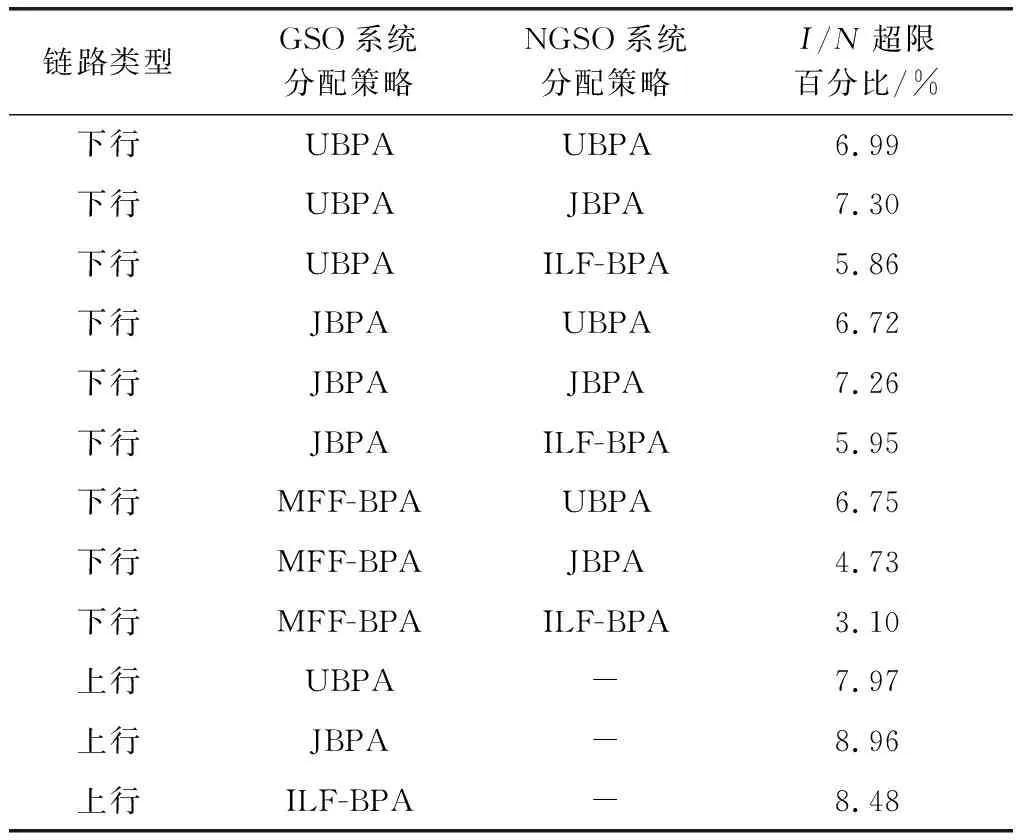
表5 INR I/N超過-12.2 dB限值的對比結果Table 5 Comparison results of the I/N exceeding the limit of -12.2 dB

如表5所示,對于NGSO-GSO上行鏈路干擾場景,受擾GSO衛星系統每個地球站發射機的波束數量為2的情況下,ILF-BPA分配策略與其他策略的I/N超限百分比偏差不超過0.51%;對于下行鏈路干擾場景,在受擾GSO衛星系統為同一種分配策略條件下,干擾NGSO星座系統采用ILF-BPA策略,相比于其他兩種分配策略,在保證波束滿足建鏈條件的情況下,I/N超限百分比降低了0.77%～3.65%;在干擾NGSO星座為同一種分配策略條件下,受擾GSO衛星采用MFF-BPA策略,相比于其他兩種分配策略,I/N超限百分比基本上降低了0.24%～2.85%。

在相同的波束及空口參數條件下,以下行鏈路為例,考慮到將所提方法與其他相關文獻方法就干擾評估效果進行對比分析。圖12主要涉及引言部分提到的文獻[4,10-11,13-14]所采用的NGSO-GSO頻率干擾分析方法。

如圖12所示,相比于上述文獻,當GSO和NGSO系統同時采用所提的MFF-BPA及ILF-BPA策略時,I/N超限百分比基本上降低了1.41%～3.88%,進一步驗證了所提方法的有效性。

5 結 論

在NGSO-GSO干擾場景中:提出了一種考慮融合功率分配策略的干擾計算方法,該方法融合了空間特征、波束業務特征及信道特征,支持系統級的定量化計算分析;針對提出的NGSO和GSO系統的功率分配策略,分別設計了相對應的上下行鏈路的目標函數和非線性約束,該策略結合了建鏈特征;定量化對比分析了融合功率分配策略對緩解系統間干擾的作用,在下行鏈路干擾計算分析時,當干擾NGSO星座分配策略不變時,受擾GSO衛星采用提出的MFF-BPA策略,相比于UBPA、JBPA策略,I/N超限百分比降低了0.24%～2.85%;當受擾GSO系統分配策略不變時,干擾NGSO星座采用ILF-BPA策略,相比于UBPA和JBPA策略,I/N超限百分比降低了0.77%～3.65%。

本文所提出的方法可作為NGSO-GSO系統間下行鏈路的頻率干擾分析的參考。在現有實驗條件下,融合功率分配策略對上行I/N超限百分比的緩解作用不明顯,后續將進一步研究。此外,本文重點研究Ku/Ka頻段的NGSO-GSO系統間的干擾分析,后續將在此基礎上,考慮其他頻段的頻率共用特點和信道特征,進一步探討緩解NGSO星座對GSO系統干擾的有效手段。