變量相關性對隧道二次襯砌可靠指標的影響

趙東平，吳 楠，涂懷宇

（1. 西南交通大學交通隧道工程教育部重點實驗室，四川成都 610031；2. 西南交通大學土木工程學院，四川成都 610031）

長期以來，我國鐵路隧道結構設計主要采用安全系數法，這種方法與國際上普遍采用的極限狀態法存在較大差異。為與國際標準接軌，自2011年以來，諸多學者在鐵路隧道極限狀態設計方法領域展開了系統研究，部分成果已經納入相關規范。趙東平等［1］采用校準法對不同時速的隧道襯砌結構可靠指標開展了研究，提出我國鐵路隧道襯砌承載能力極限狀態的目標可靠指標建議值；宋玉香等［2］運用Monte Carlo 隨機有限元法對復合式襯砌進行了計算研究，提出抽樣次數的建議值，得出隨機變量的分布特征和各參數的敏感性特征；李奎等［3］對素混凝土襯砌可靠度計算模型的研究表明，作用效應和結構抗力的概率分布類型直接影響襯砌可靠度指標計算方法和計算結果的合理性；譚忠盛等［4］通過對各種結構可靠度算法的比較分析，提出了一種簡便實用的二次二階矩法進行隧道襯砌結構可靠度分析，與改進蒙特卡羅法的對比結果表明，其提出的新方法具有較高的精度；宋玉香等［5］對比分析了響應面法計算結果和Monte Carlo法抽樣10 萬次計算結果，發現兩者具有較高的一致性，驗證了響應面法可應用于隧道襯砌的可靠性分析；余永康等［6］采用假定隧道襯砌結構隨機變量相關性系數的方法，分析了變量相關性對結構作用效應的影響，結果表明隨機變量之間的相關性會對隧道結構的效應產生較大的影響；李曉軍等［7］采用數據表（Spreadsheet）法與Monte Carlo 法對盾構襯砌的2 種極限狀態進行可靠度分析，結果表明兩者誤差不超過4%，但Spreadsheet法可節省大量計算時間；蘇永華等［8-11］通過理論研究和公式推導，提出了多種隧道結構可靠度指標分析方法，并將這些方法的計算結果與蒙特卡羅法的精確解進行對比，驗證了所提方法具有較高準確性；Guo等［12］對隧道支護襯砌進行了可靠性分析，結果表明土體空間變異性對隧道襯砌可靠度有顯著影響；Hamrouni 等［13］、Lü 等［14-15］采用響應面法和二階可靠度計算方法對隧道隨機變量的相關性和分布形態開展研究，結果表明考慮摩擦角和黏聚力的相關性會對計算結果產生顯著影響。

分析上述成果可知，既有研究聚焦于隧道襯砌隨機變量的統計特征、隧道襯砌參數敏感性及土體變量相關性等方面，且研究過程中未考慮襯砌結構設計表達式中隨機變量的相關性問題。根據可靠度相關計算理論可知，基本隨機變量的相關性與結構功能函數的失效概率相關，即隨機變量的相關性與可靠指標有關。

本文依托京張高鐵新八達嶺隧道工程，采用Monte Carlo 隨機有限元方法對隧道襯砌結構設計中的隨機變量進行抽樣計算，通過確定各個隨機變量的相關性系數求解考慮隨機變量相關性的隧道襯砌可靠指標，并論證隨機變量相關性對隧道襯砌結構截面可靠指標的影響。

1 設計變量相關性

隧道襯砌是偏心受壓構件，根據圍巖級別和埋深不同，可采用素混凝土或鋼筋混凝土襯砌。為了分析隧道襯砌結構設計中隨機變量的相關性，首先要建立素混凝土襯砌和鋼筋混凝土襯砌的極限狀態方程。

1.1 極限狀態方程

根據截面受力狀態不同，素混凝土襯砌可分為受壓和受拉2 種控制狀態。2 種狀態下對應的襯砌結構極限狀態方程［16］分別為

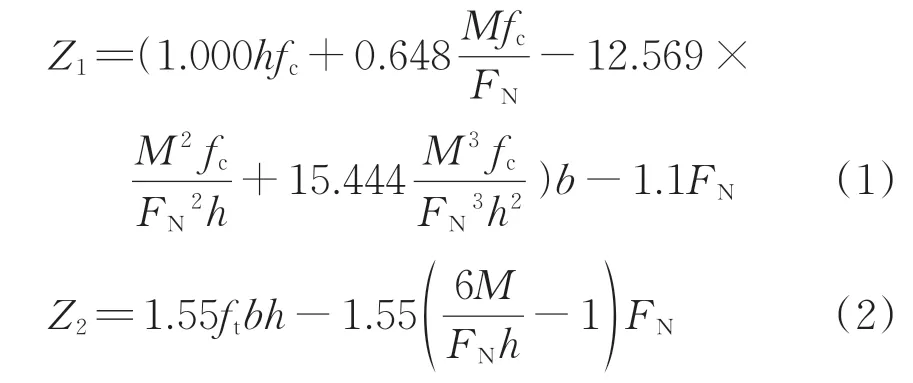
式中：Z1和Z2分別為素混凝土襯砌受壓和受拉控制時的極限狀態功能函數；h為襯砌截面高度；fc為混凝土軸心抗壓強度設計值；M為襯砌截面所受彎矩；FN為襯砌截面所受軸力；b為襯砌截面寬度；ft為混凝土軸心抗拉強度設計值。

根據受壓區高度不同，鋼筋混凝土襯砌可分為大偏心受壓和小偏心受壓2 種受力狀態。2 種狀態下的襯砌結構極限狀態方程均為

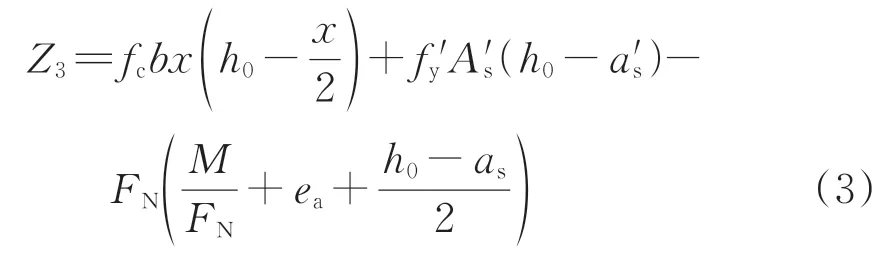
式中：Z3為鋼筋混凝土襯砌受力時的極限狀態功能函數；x為混凝土受壓區高度；h0為襯砌截面有效高度；f'y為鋼筋抗壓強度設計值；A's為受壓區縱向鋼筋截面面積；a's為受壓區縱向鋼筋合力點至襯砌截面受壓邊緣的距離；ea為附加偏心距；as為受拉區鋼筋合力點至襯砌截面近邊的距離。

1.2 變量相關性系數

由式（1）—式（3）可知，隧道襯砌結構極限狀態方程中涉及多個隨機變量，如果這些隨機變量之間存在相關性，則可能會對襯砌截面失效概率產生影響。為了確定上述變量之間的相關性，首先要確定式（1）—式（3）中任意2 個隨機變量之間的相關性系數。

根據概率理論可知，任意2個隨機變量X1，X2之間是否具有相關性以及相關程度大小可通過相關系數ρX1X2來評價，ρX1X2可表示為［17］

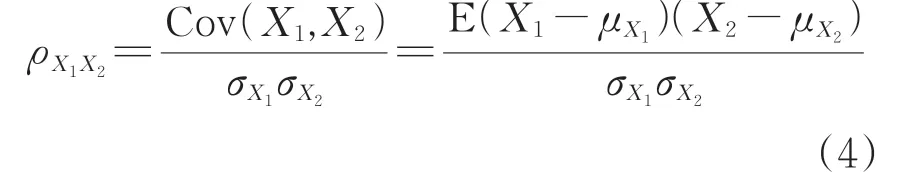
式中：σX1，σX2分別為變量X1，X2的標準差；Cov(X1，X2)為變量X1，X2的協方差；μX1，μX2分別為變量X1，X2的均值。

當統計計算得出ρX1X2=0 時，說明2 個變量不存在相關性；當0 ＜|ρX1X2|＜1 時，說明2 個變量之間存在相關性；當|ρX1X2|=1 時，說明2 個變量之間存在強相關性。

式（4）僅能表示2 個隨機變量之間的相關性，在式（1）—式（3）的極限方程中涉及多個變量，為便于計算，可將任意2 個變量之間的相關性系數組合為相關性系數矩陣。

對于素混凝土襯砌結構，截面受壓和受拉控制狀態的相關系數矩陣RSc和RSt分別為

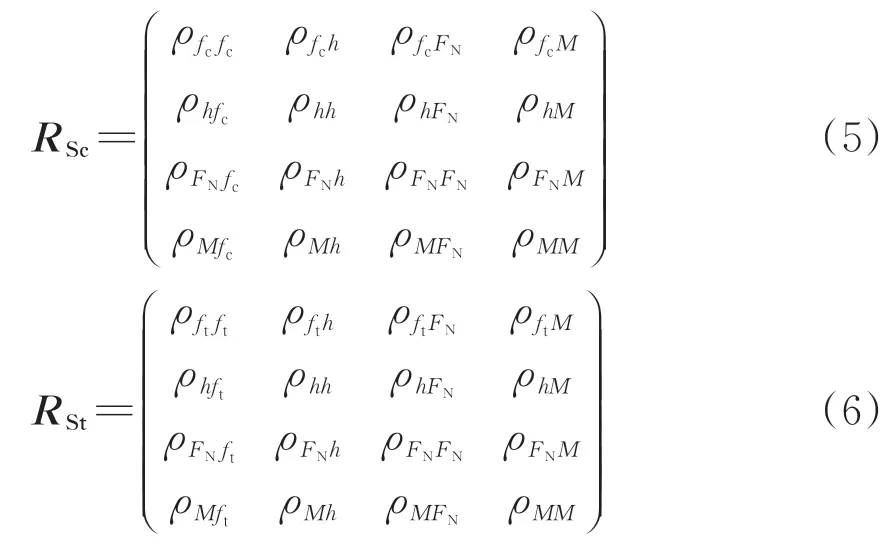
對于鋼筋混凝土襯砌結構，其相關系數矩陣RG為

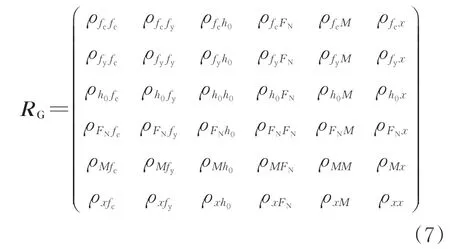
在式（5）—式（7）中相關性系數矩陣參量的下標表示該系數參量對應的2個變量。

1.3 變量相關性對可靠指標的影響

以二維連續分布隨機變量為例，當變量存在相關性時，其聯合概率密度函數f(X1，X2)［18］為

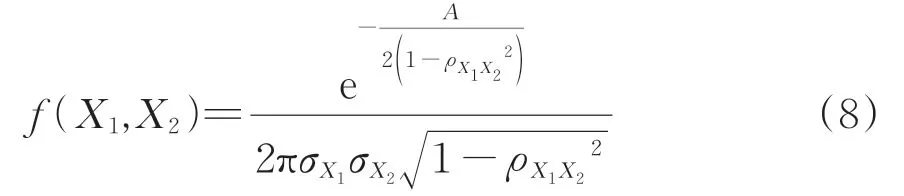
其中，

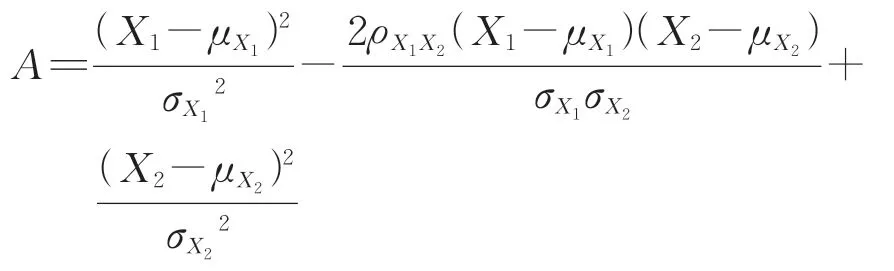
對于一般結構而言，功能函數可簡化為抗力R與效應S的函數，即功能函數Z=R-S。假設R和S均為正態分布，且R和S的聯合概率密度函數為f(R，S)，則功能函數的失效概率Pf為

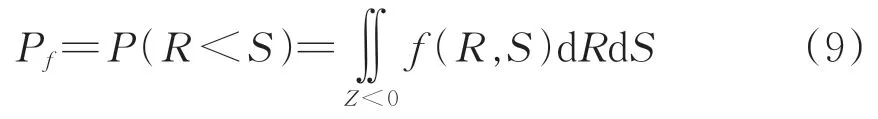
當隨機變量R和S相互獨立時，即ρRS=0，聯合概率密度函數f(R，S)為

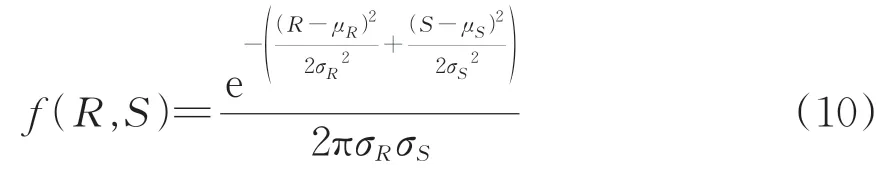
當隨機變量R和S具有相關性時，即|ρRS|≤1且ρRS≠0，聯合概率密度函數f(R，S)為

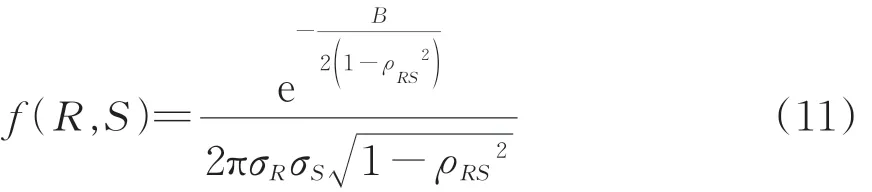
其中，

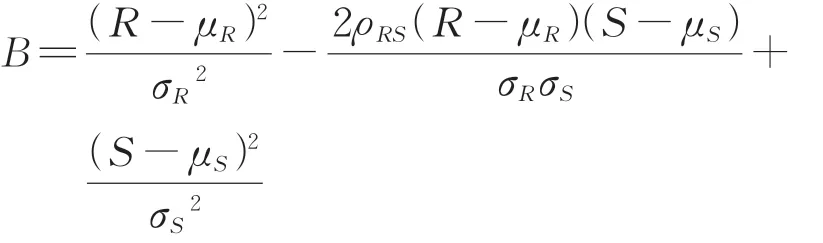
由式（8）—式（11）可知，當隨機變量R和S相關時，其聯合概率密度函數f(R，S)的表達式不同，功能函數的失效概率也不同，因此隨機變量的相關性會影響結構失效概率，進而影響結構可靠指標的計算結果。

目前，用于求解可靠指標的方法主要有驗算點法、響應面法及數據表法等。當考慮變量相關性時，數據表法［19-21］相對簡便，且形象直觀。根據該方法的計算公式，通過Excel 編程可實現考慮相關性的可靠指標計算。

根據數據表法，可靠指標β可由隨機變量矩陣、隨機變量均值矩陣及協方差矩陣之間通用矩陣運算后求得，其計算表達式為

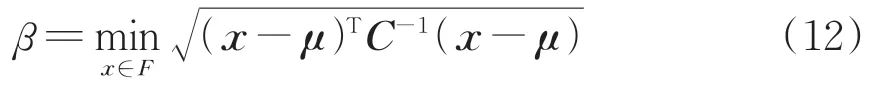
式中：x為多元正態分布隨機變量矩陣，當x為其他分布時，可通過當量正轉換為正態分布后再進行計算；F為失效域；μ為隨機變量均值矩陣；C為變量協方差矩陣，可由式（13）表示，協方差矩陣中的元素可采用式（5）—式（7）確定的相關系數根據式（4）計算獲得。

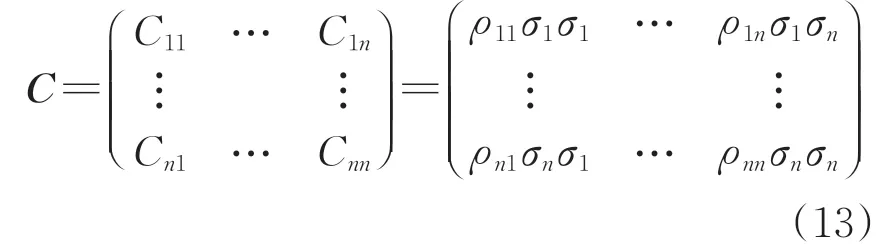
在隨機變量空間內，可靠指標的物理含義由式（14）解釋，該式表示空間的1個橢球。

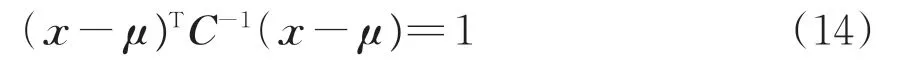
隨機變量為二維時，式（14）表示平面內的1個橢圓，橢圓中心在變量均值處；當相關系數ρ=0 時，橢圓的長、短軸分別為σ1和σ2；隨著相關系數的變化，橢圓形狀也相應改變。橢圓與相關系數的關系如圖1所示。

圖1 橢圓與相關系數關系

根據上述原理，當標準差變化β倍后，可得到橢圓與極限狀態面相切時的方程式為

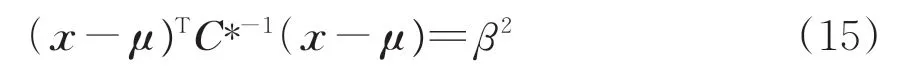
式中：C*為標準差改變β倍后對應的協方差矩陣。

由于此時橢圓與極限狀態面相切，故所求得的β值即為要求的可靠指標，如圖2所示。

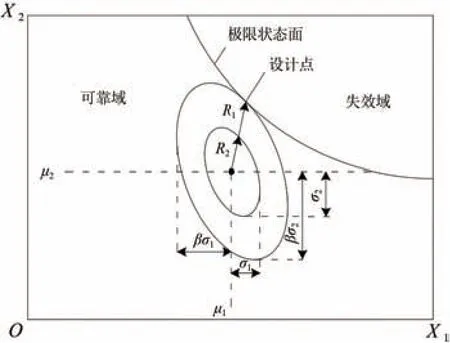
圖2 數據表法可靠指標的確定

2 可靠指標求解

在計算襯砌可靠指標時，首先要確定極限狀態方程中隨機變量之間的相關性，為此需要進行統計抽樣。運用開發的TRAS V1.0 程序，采用Monte Carlo 隨機有限元分析與數據表法相結合的方法計算考慮隨機變量相關性的襯砌結構可靠指標值。新八達嶺隧道工程中的Ⅳ，Ⅴ級圍巖深埋地段分別采用素混凝土和鋼筋混凝土襯砌，以下分別展示隧道襯砌可靠指標的求解過程。

2.1 計算模型

新八達嶺隧道Ⅳ，Ⅴ級圍巖深埋襯砌結構尺寸如圖3所示。

根據圖3所示的結構幾何尺寸基于荷載-結構法建立有限元數值模型，采用二維梁單元模擬襯砌，二維桿單元模擬圍巖對襯砌的約束作用，模型劃分為38個單元，如圖4所示。

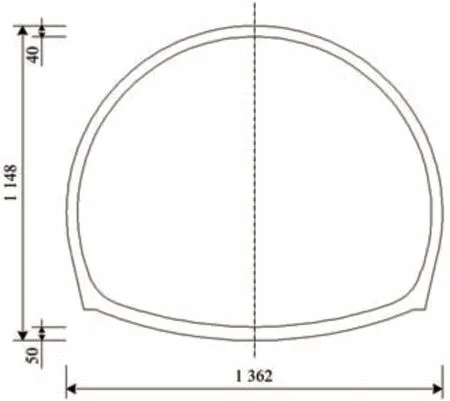
圖3 Ⅳ級圍巖深埋襯砌（單位：cm）

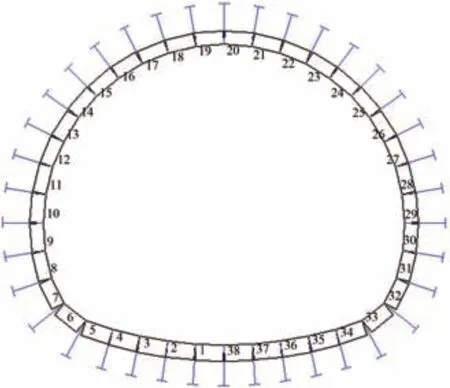
圖4 襯砌結構可靠性計算模型

2.2 素混凝土襯砌

隧道襯砌結構可靠度計算的難點在于襯砌是多次超靜定結構，襯砌截面內力無顯式表達式，因此要采用隨機有限元抽樣計算的方法獲取內力的樣本數據。

Ⅳ級圍巖襯砌采用C30素混凝土，二次襯砌承受荷載比例取50%，此前關于結構材料、圍巖彈性反力系數及側壓力系數等基本隨機變量的統計特征值已有較全面的研究，本文根據前期研究成果確定了圍巖重度、彈性模量、側壓力系數、混凝土軸心抗拉強度、襯砌厚度及彈性反力系數等統計特征［22］，具體見表1。

表1 Ⅳ級圍巖深埋隧道襯砌基本隨機變量統計特征

經驗表明，采用Monte Carlo 隨機有限元法進行隨機抽樣時，若樣本容量有限，會對計算結果產生較大影響。為確定抽樣次數，使襯砌結構內力統計特征計算結果不受抽樣次數的影響，以襯砌拱頂20 號單元為例進行試算，得到軸力和彎矩值樣本歷史曲線，如圖5和圖6所示。

由圖5和圖6可知：拱頂截面軸力及彎矩的均值和標準差變化曲線在抽樣5 000次時仍有較大變化，抽樣7 500次時趨于平緩，抽樣1萬次時趨于穩定。

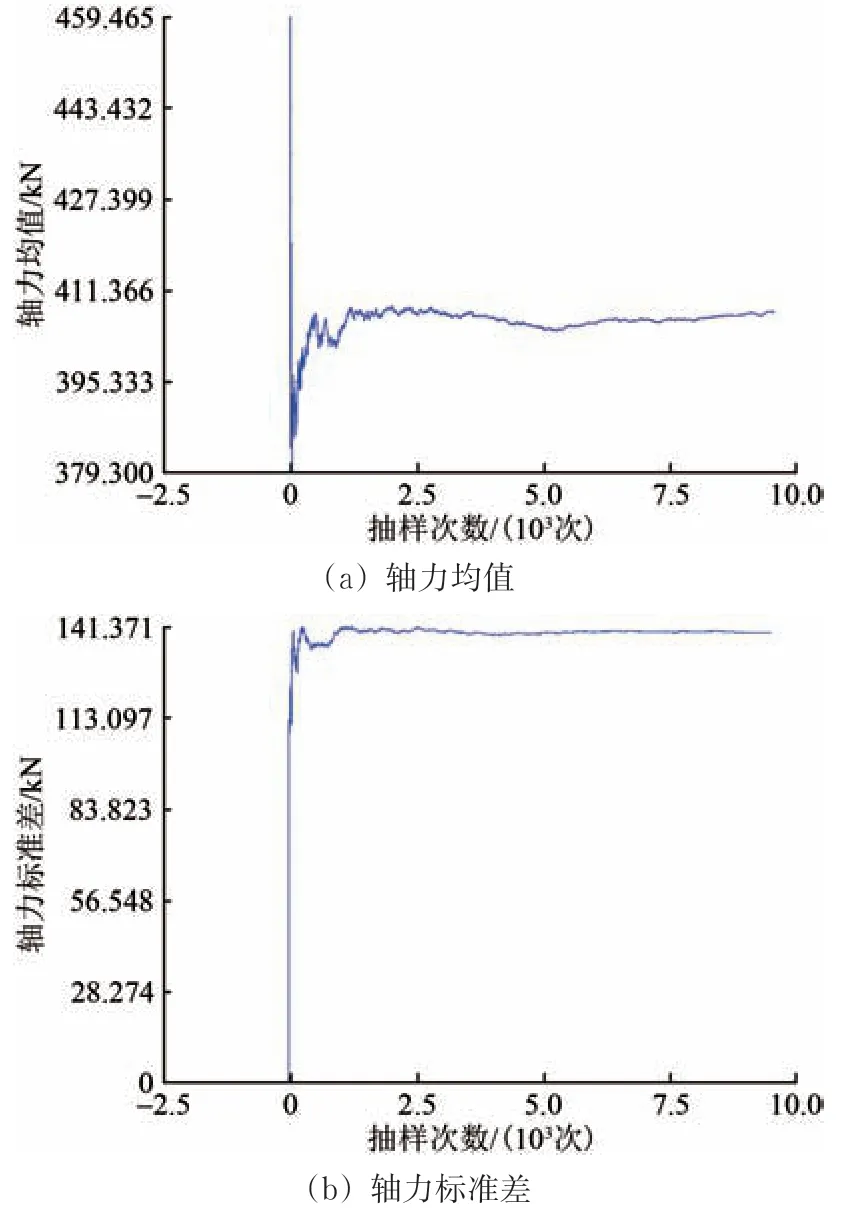
圖5 20號單元軸力樣本曲線

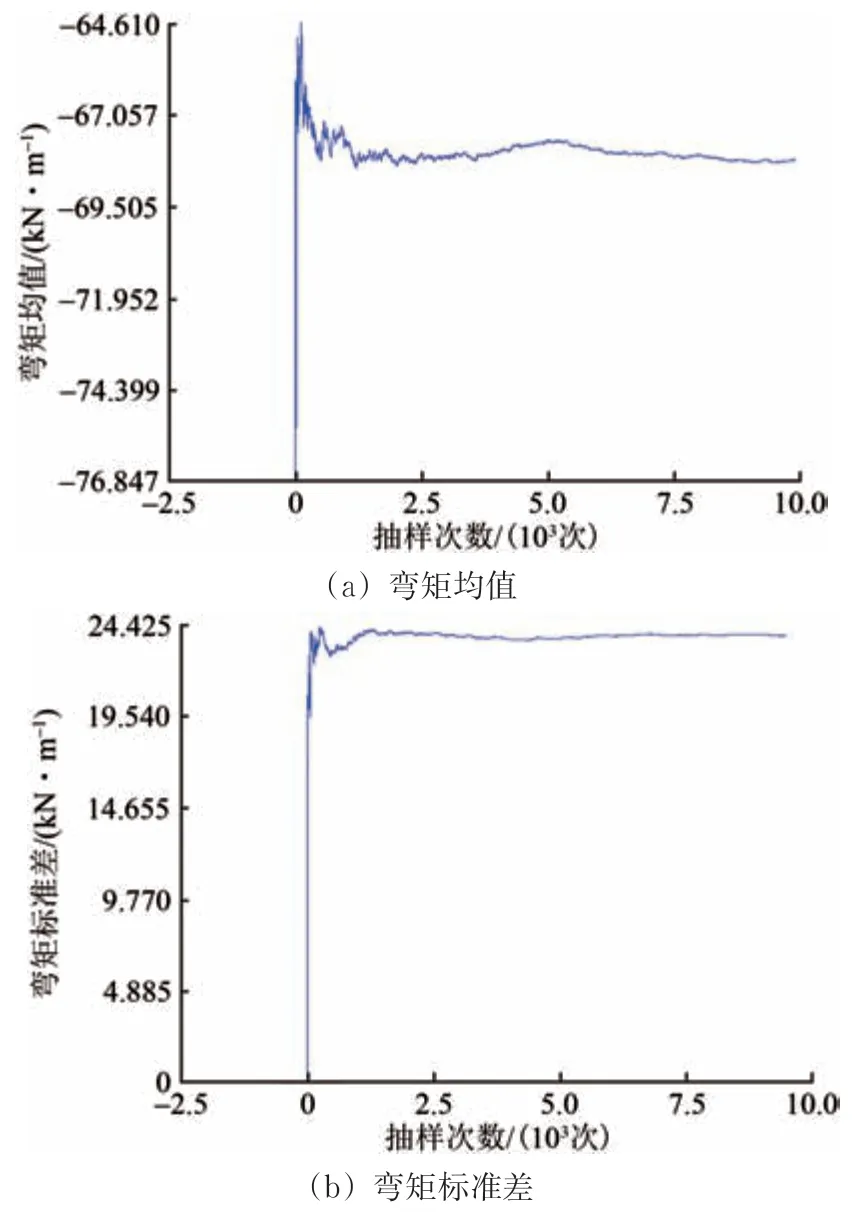
圖6 20號單元彎矩樣本曲線

襯砌其余截面內力抽樣數據的統計特征與拱頂20號截面相似，出于保守考慮確定抽樣為1萬次進行計算。

對襯砌1 個橫斷面上的38 個單元分別抽樣1 萬次，即獲得了1 個全截面的抽樣數據，通過式（4）計算可得到兩兩變量之間的相關系數。仍以襯砌拱頂20 號單元為例，計算得到隨機變量的相關系數矩陣為

由式（16）可知，除彎矩與軸力之間的相關系數接近于1、具有較強相關性外，其他變量之間的相關系數幾近于0，相關性并不明顯，故主要考慮彎矩與軸力之間的相關性對計算結果的影響。

對抽樣數據進行分析計算，得到該截面襯砌結構內力的統計特征見表2。

表2 襯砌結構內力統計特征

以式（16）和表2中數據為已知參數，根據式（13）計算可得20號單元的協方差矩陣為

根據上述算法，襯砌每一個單元均可計算得出1 個協方差矩陣。根據數據表法，在Excel 中編制相關計算公式，即可求解考慮變量相關性的襯砌各個截面可靠指標。

在Excel 中輸入各隨機變量的均值、標準差、相關系數矩陣，通過計算得到協方差矩陣和協方差逆矩陣，并編寫極限狀態功能函數，通過Excel 的規劃求解功能計算可靠指標。具體方法為：在“規劃求解參數”中，將“設置目標”設置為可靠指標單元格，設置目標為“最小值”；將“可變單元格”設置為試算值單元格，約束條件設置功能函數值小于或等于0；選擇迭代求解方法為“非線性”；點擊求解后，“可靠指標”單元格即輸出求得的可靠指標。

對每一個單元，分別按上述流程進行計算求解，即可得到Ⅳ圍巖素混凝土襯砌考慮變量相關性的全截面可靠指標，將可靠指標計算值及差異值、截面偏心距及其抗裂、抗壓控制標準0.2h等參數編制于1 張圖上，如圖7所示。

圖7 素混凝土襯砌可靠指標計算結果

為更為直觀地將截面可靠指標與襯砌橫斷面的位置關系對應起來，將每個截面考慮可靠相關性與不考慮相關性時計算得到的可靠指標繪制于襯砌截面上，如圖8所示。圖中：“＋”表示軸力與彎矩變量之間呈現正相關性。

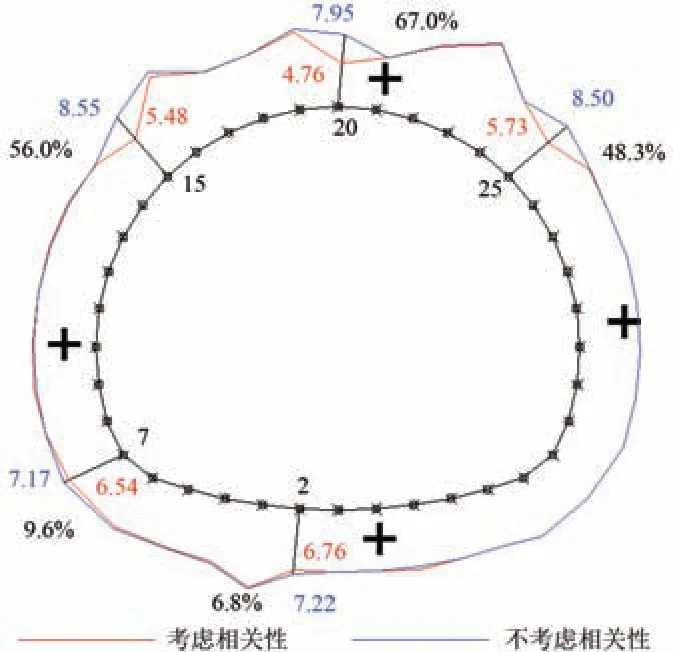
圖8 素混凝土襯砌可靠指標包絡圖

由圖7和圖8可知：15，20 及25 號3 個襯砌單元截面偏心距均大于0.2h，屬于抗裂極限狀態控制；其余斷面偏心距均小于0.2h，屬于抗壓極限狀態控制；素混凝土襯砌各單元軸力與彎矩均呈現正相關性；對于抗壓極限狀態，考慮隨機變量相關性與不考慮隨機變量相關性的可靠指標計算值，除在仰拱截面和左墻角截面差異值達到6.8%和9.6%外，其余各單元兩者差異均小于4%，平均差異為1.2%，即兩者的可靠指標結果基本一致；對于素混凝土襯砌抗裂極限狀態，考慮隨機變量相關性與不考慮隨機變量相關性的可靠指標計算值，兩者差異在拱頂截面達到最大為67.0%，在左、右拱腰截面差異值分別為56.0%和48.3%，其余各單元兩者差異均小于7%，平均差異為30.3%，即兩者的可靠指標計算結果差異較大。

2.3 鋼筋混凝土襯砌

V 級圍巖襯砌采用C35 鋼筋混凝土，結構材料、圍巖彈性反力系數及側壓力系數等基本隨機變量的統計特征值具體見表3。

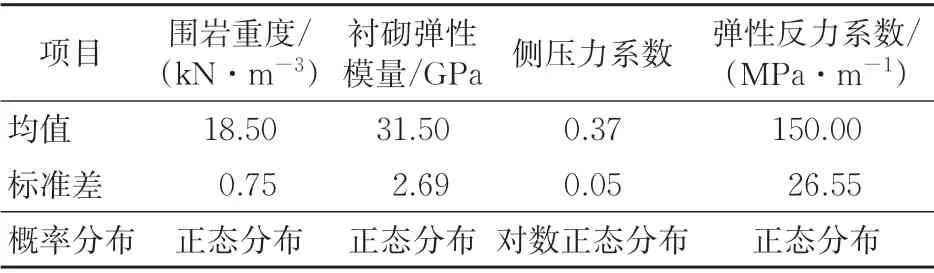
表3 V級圍巖深埋隧道襯砌基本隨機變量統計特征

采用與素混凝土襯砌相同的計算方法，計算得到鋼筋混凝土襯砌各單元的可靠指標如圖9和圖10所示。圖9中：可靠指標值的正負分別表示軸力FN與彎矩M之間相關性的正負；ξbh0為界限受壓區高度，其中ξb為相對界限受壓區高度。圖10中：“＋”、“－”分別表示軸力與彎矩變量之間相關性的正負。

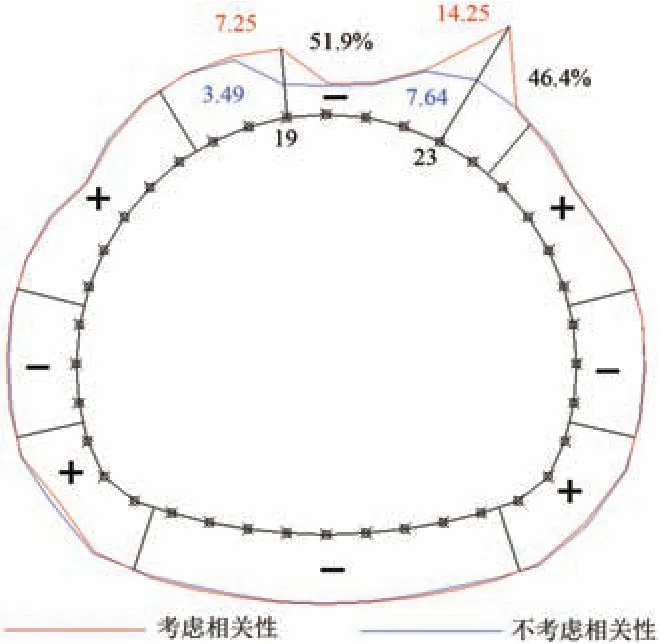
圖10 鋼筋混凝土襯砌可靠指標包絡圖

由圖9可知：14，19，20，21及26號5個襯砌單元截面受壓區高度小于界限受壓高度ξbh0，屬于大偏心受壓狀態，其余襯砌單元均屬于小偏心受壓狀態。

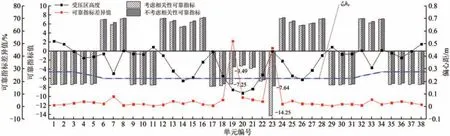
圖9 鋼筋混凝土襯砌可靠指標計算結果

由圖10 可知：鋼筋混凝土襯砌各單元軸力與彎矩在仰拱、邊墻及拱頂截面呈現負相關性，在拱腰及拱腳截面呈現正相關性；對于鋼筋混凝土襯砌小偏心受壓截面，考慮隨機變量相關性與不考慮隨機變量相關性的可靠指標計算值，除在右拱腰截面兩者差異值為46.4%（23 號單元）外，其余各單元兩者差異均小于8%，平均差異為3.9%，即兩者的可靠指標結果基本一致；對于鋼筋混凝土襯砌大偏心受壓截面，考慮隨機變量相關性與不考慮隨機變量相關性的可靠指標計算值，兩者差異在拱頂截面達到最大為51.9%（19 號單元），其余各單元兩者差異均小于8%，平均差異為21.6%，即兩者的可靠指標計算結果差異較大。

總體而言，當軸力與彎矩負相關時，考慮變量相關性的計算可靠指標偏大；當軸力與彎矩正相關時，考慮變量相關性的計算可靠指標偏小。

3 結 論

（1）基于2 個綜合隨機變量概率密度函數的表達式，推導出考慮變量相關性時聯合概率密度函數的表達式，論證了考慮變量相關性與否會對失效概率的計算結果產生影響。

（2）鐵路隧道襯砌的隨機變量中，軸力與彎矩之間相關性較強，對可靠指標的計算結果影響較為顯著。當變量之間呈現正相關性時，考慮隨機變量相關性的可靠指標計算結果偏小；當變量之間呈現負相關性時，考慮隨機變量相關性的可靠指標計算結果偏大。

（3）對于素混凝土襯砌，結構各單元軸力與彎矩均呈現正相關性。隨機變量相關性對結構抗壓控制狀態截面的可靠指標影響較小；對抗裂控制狀態截面的可靠指標影響較大，在拱頂截面考慮相關性后的可靠指標值比不考慮時減小67.0%。

（4）對于鋼筋混凝土襯砌，結構各單元軸力與彎矩在仰拱、邊墻及拱頂截面呈現負相關性，在拱腰和拱腳截面呈現正相關性。隨機變量相關性對結構小偏心受壓控制狀態截面的可靠指標影響較小，僅在右拱腰截面考慮相關性后的可靠指標值比不考慮時增大46.4%；隨機變量相關性對大偏心受壓控制狀態截面的可靠指標影響較大，拱頂截面考慮相關性后的可靠指標值比不考慮時增大51.9%。

（5）采用極限狀態法設計鐵路隧道襯砌時，宜考慮變量相關性對結構可靠性的影響。對于素混凝土襯砌，可適當提高混凝土強度或增加襯砌厚度，從而保證結構可靠性；對于鋼筋混凝土襯砌，可適當減少配筋量以合理利用結構承載能力，從而控制建造成本。