基于RPP 串聯機構的固定式割膠機設計與仿真分析＊

高 鋒 孫江宏② 何宇凡 李乃崢 高可可

（①北京信息科技大學機電工程學院，北京 100192；②清華大學機械電子工程研究所，北京 100084）

天然橡膠是不可替代的重要戰略物資和工業材料，目前的人工割膠方式勞動強度大、技術要求高、工作效率低，遠不能滿足我國對天然橡膠的需求[1-3]。割膠工具是影響天然橡膠產量的決定性因素，因此通過現代科學技術實現割膠生產的機械化與智能化迫在眉睫[4-5]。

目前割膠設備主要以固定式割膠機為主[6-9]。張春龍等研制了一種基于三坐標軸的固定式割膠機，但框架結構只能對單一高度割面實施割膠作業，無法實現全方位割膠[10]。許振昆等基于圓柱坐標系發明的固定式割膠機，切割深度無法控制，不能保證橡膠樹使用壽命[11]。吳米等結合割線特點研制的固定式割膠機，連接結構采用支點接觸，易造成受力不均，設備穩定性無法保證[12]。張俊雄等發明了一種可實現下刀、行刀和收刀一體化的固定式割膠機，但需要操作者拉動滑座實現割膠作業，無法實現全自動割膠[13]。韓青江結合割膠技術難點設計的固定式割膠機，可設定不同割線斜度和切割深度，但無法實時控制[14]。

本文設計了一種新型固定式割膠機。該割膠機具有三自由度、可實現復雜空間曲線運動、滿足不同切割深度以及割線斜度。同時該機構具有多輸入多輸出、非線性和位置時變等特點，故采用機器人理論將該機構等效成RPP 模型，對其進行運動學和動力學求解與仿真。

1 結構設計

1.1 人工割膠過程分析

割膠過程如圖1a 所示，首先需標定前后水線的位置，入刀點在后水線上，收刀點在前水線上，割面開角為1/4 樹周。在進行割膠工作過程中，工人手持膠刀，以入刀點為起點，沿割線自右下至左上切割樹皮，使膠乳從割口處流出，以收刀點為終點，結束一次割膠工作。為保證橡膠樹經濟壽命，前后兩次割線之間的軸向距離需要控制在1.3 mm 以內。

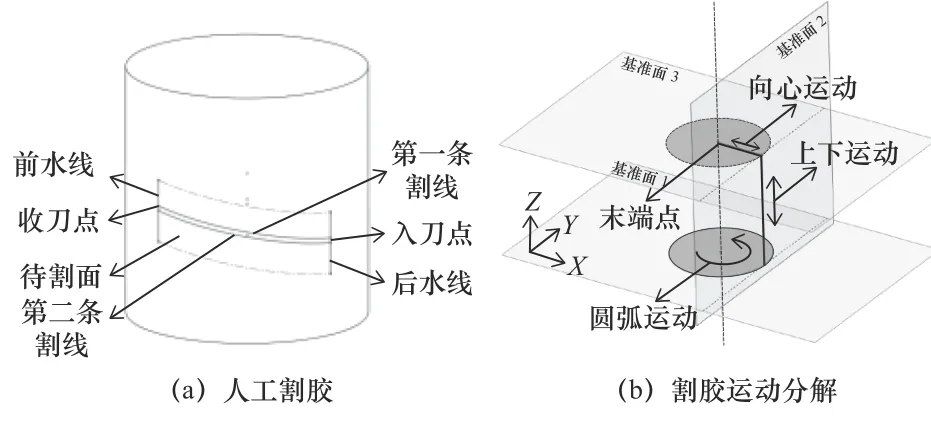
圖1 割膠過程

在割膠作業過程中有割深、高度和弧度3 個重要指標。割深指樹皮表面至割口的距離，由于橡膠樹內部產膠層距離樹皮表面約為5～6 mm，因此需要控制切割深度。高度指入刀點至收刀點沿樹干軸向方向的距離，弧度指后水線至前水線沿橡膠樹樹皮所掃過的角度。割線斜度需控制在25°～30°，因此需要對高度和弧度進行控制[15-16]。

人工割膠過程中所產生的割線是一段近似圓柱螺旋線的復雜空間曲線。為了實現割線軌跡，可將人工割膠過程分解為3 個不同空間平面運動，如圖1b 所示。

在圖1b 中，垂直于樹干軸心的徑向運動可實現割深控制；沿樹干方向的上下軸向運動可實現高度控制；繞樹干軸心轉動的圓弧運動可實現弧度控制。將徑向運動、上下軸向運動以及圓弧運動組合，3 個不同空間平面的運動軌跡共同作用于向心運動的末端點，實現復雜空間曲線。

1.2 一種新型固定式割膠機結構設計

根據上述3 個不同空間平面運動及其運動關系，設計一種新型固定式割膠機，分為固定機構、圓弧軌道以及割膠工作模塊3 部分，如圖2 所示。固定機構將設備固定在橡膠樹上；上頂板與下底板均安裝有滾輪與圓弧軌道上的“凹”字型軌道配合，限制割膠工作模塊的運動方式。割膠工作模塊中的傳動齒輪組、運動轉軸和運動轉軸兩端的傳動齒輪組成齒輪傳動模塊。

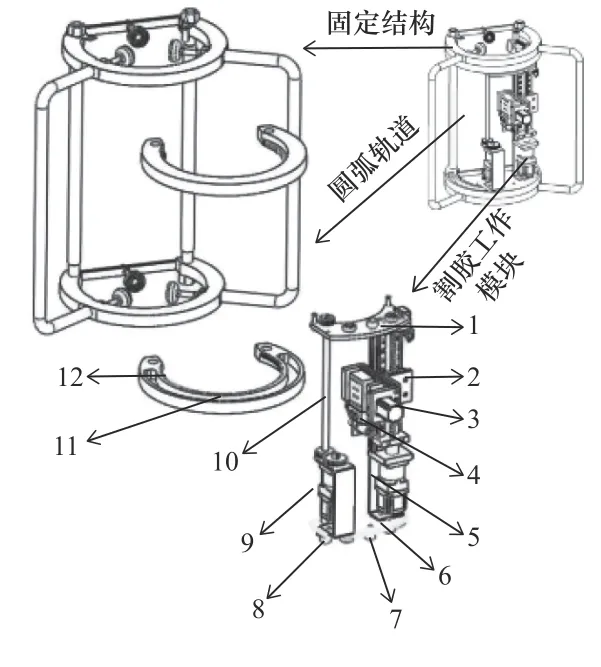
圖2 固定式割膠機

傳動齒輪組9、絲杠傳動模塊3和絲杠傳動模塊5 均可相對獨立運動。傳動模塊通過傳動齒輪組9 轉動帶動運動轉軸10 轉動，運動轉軸10 兩端各有一個傳動齒輪8，傳動齒輪8 與圓弧軌道上的內齒圈嚙合帶動割膠工作模塊實現某一圓心角度的圓弧運動。絲杠傳動模塊5和絲杠傳動模塊3 可分別實現滾珠絲杠滑臺模組中滑臺的上下軸向運動以及徑向運動。傳動齒輪組9、絲杠傳動模塊5和絲杠傳動模塊3 分別通過上頂板與下底板以及L 型板2集成在一起，通過3 個傳動模塊空間運動的疊加實現膠刀的復雜空間曲線軌跡。

2 新型固定式割膠機理論分析

2.1 理論模型構建

通過機器人學對新型固定式割膠機的關鍵部件及部件之間的運動關系進行理論模型構建，如圖3a所示。

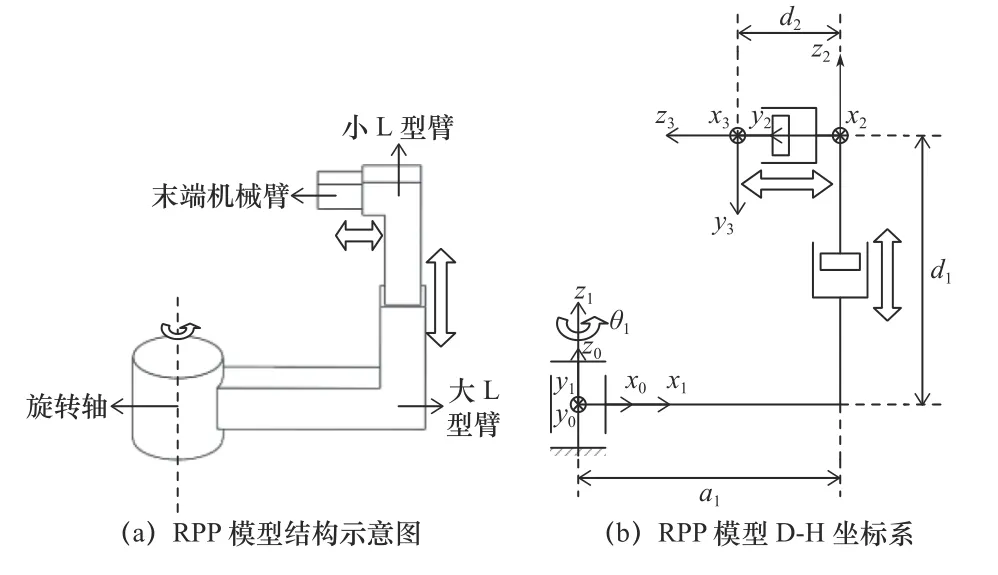
圖3 RPP 串聯機構

圖3a 中RPP 串聯機構共有3 個自由度，包括1 個轉動副和2 個移動副，旋轉軸帶動大L 型臂進行轉動，小L 型臂相對于大L 型臂可上下移動，末端機械臂相對于小L 型臂可向心移動。其中旋轉軸和大L 型臂表示齒輪傳動模塊；小L 型臂和大L 型臂表示絲杠傳動模塊1；末端機械臂和小L 型臂表示絲杠傳動模塊2和膠刀模塊[17]。

2.2 運動學模型求解

根據RPP 串聯機構模型建立D-H 坐標系[18-19]，如圖3b 所示，讀取所有相鄰連桿坐標系的D-H 參數，建立RPP 串聯機構參數表，如表1 所示。

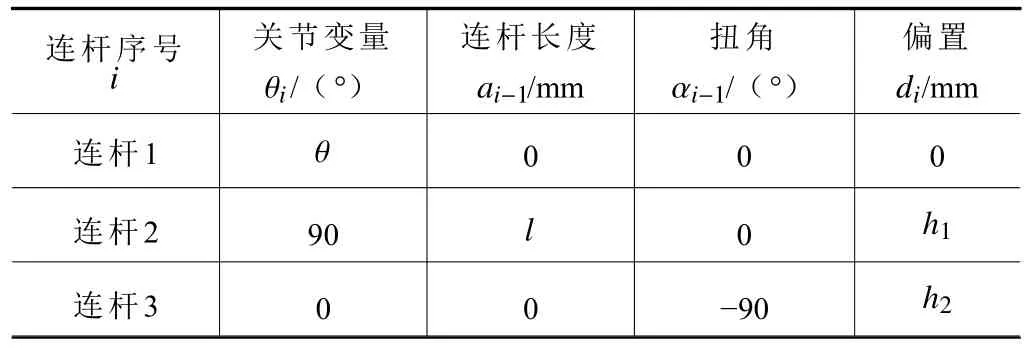
表1 RPP 串聯機構D-H 參數表

將D-H 參數表中各行參數代入D-H 矩陣通式（1）中，得：

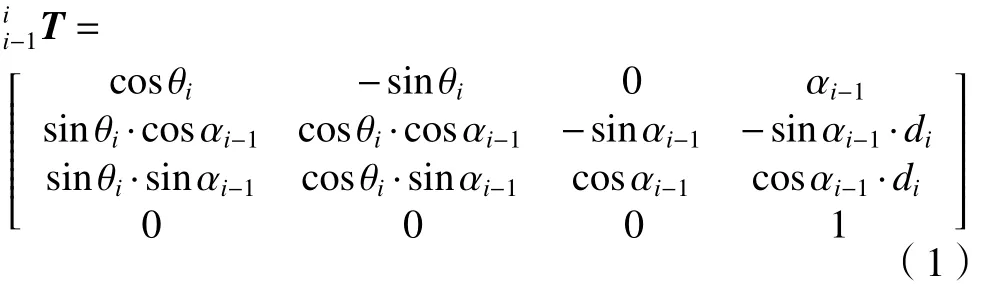
式中：i=1、2、3

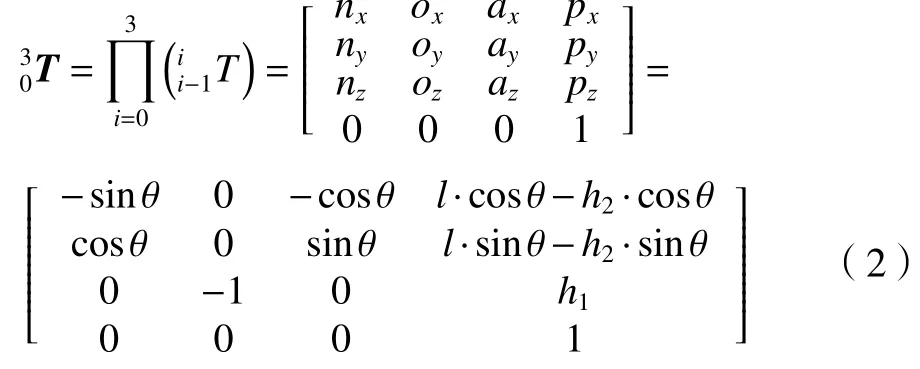
2.3 RPP 型機械臂各關節運動學分析

不同尺寸的樹圍會形成不同的割線，但每條割線均是由圓柱螺旋運動疊加反復的向心運動合成。因此在工作空間范圍內取一條理想割線，其中旋轉角度為90°，割線斜度為25°，如圖4 所示。

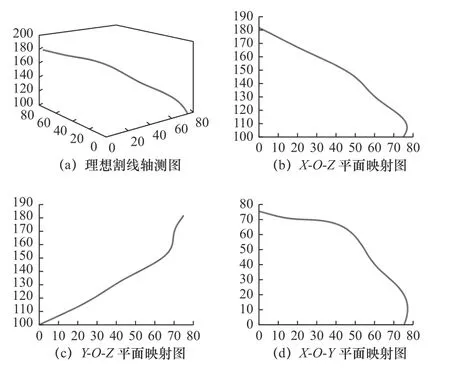
圖4 理想割線

已知笛卡爾空間下理想割線軌跡，設置仿真時長8 s，步長0.1 s。串聯機構末端點沿軌跡運動，可得各關節位移、速度和加速度隨時間變化曲線[20-22]，如圖5 所示。

從圖5 中可知，整個設備在空載狀態下，RPP串聯機構沿理想割線運動，各關節隨時間變化均呈平滑曲線，因此在運動過程中存在的振動和柔性沖擊的影響較小。

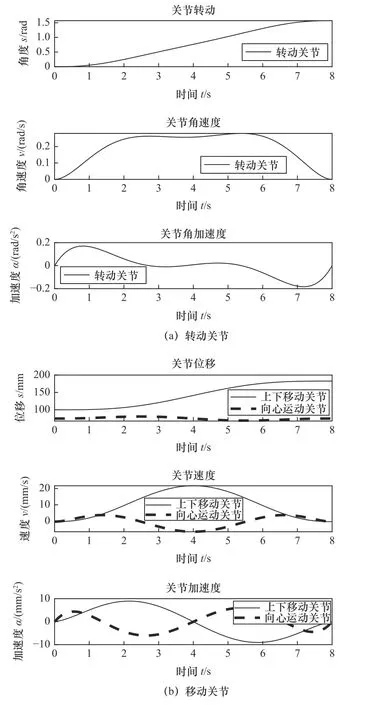
圖5 各關節隨時間變化運動曲線

2.4 動力學分析

為了檢驗RPP 串聯機構末端點沿理想割線運動時，轉動關節的轉矩以及兩個移動關節的驅動力隨時間變化是否有死點等情況，需要對各關節的Lagrange動力學方程進行求解。

首先對各連桿的質心位置進行求解：

連桿1的質心m1的位置為：

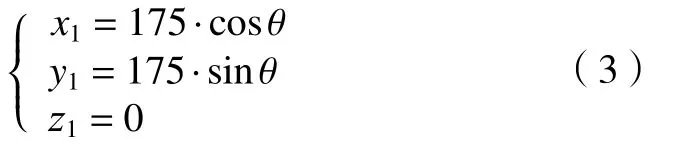
對式（3）相對于時間t求導數，可得質心m1的速度為：

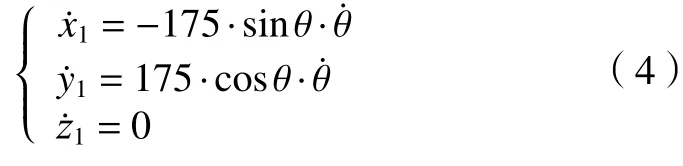
連桿2的質心m2的位置為：

對式（5）相對于時間t求導數，可得質心m2的速度為：

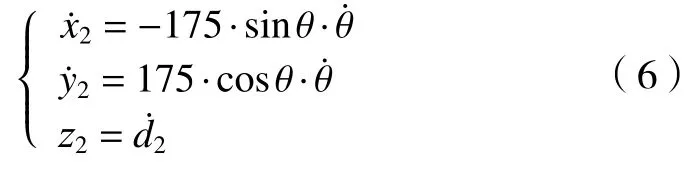
連桿3的質心m3的位置為：

其次對各連桿的速度進行求解，對式（7）相對于時間t求導數，可得質心m3的速度為：

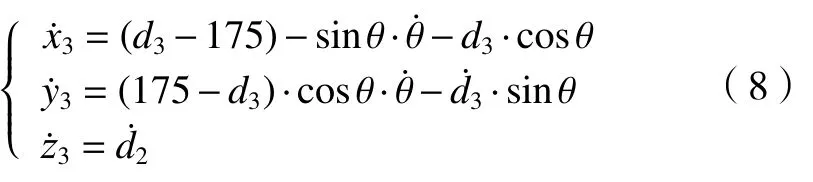
對RPP 串聯機構的總動能和總勢能以及各連桿的動能和勢能求解。質量為m，速度為的質點的動能為。分別求出連桿1、連桿2和連桿3的動能。

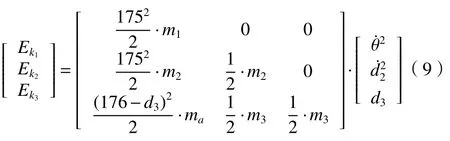
RPP 串聯機構的總動能為：

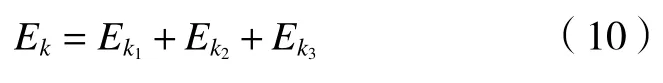
質量為m、高度為h的質點的勢能為Ep=mgh。分別求出連桿1、連桿2和連桿3的勢能。

RPP 串聯機構的總勢能為：

根據Lagrange 動力學方程

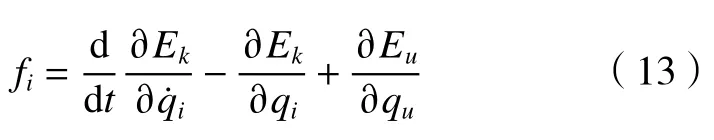
將式（8）～（12）代入式（13）中，可分別計算出關節1的轉矩、關節2和關節3的驅動力，其中m1=4.2 kg、m2=4.4 kg、m3=2.8 kg。

式中：m1、m2、m3分別為連桿1、2、3的質量。

由RPP 串聯機構各關節運動學仿真分析可知，各關節位置、速度和加速度矩陣。將上述已知條件分別代入式（14）中，可得到各關節隨時間變化轉矩以及驅動力的曲線，如圖6 所示。

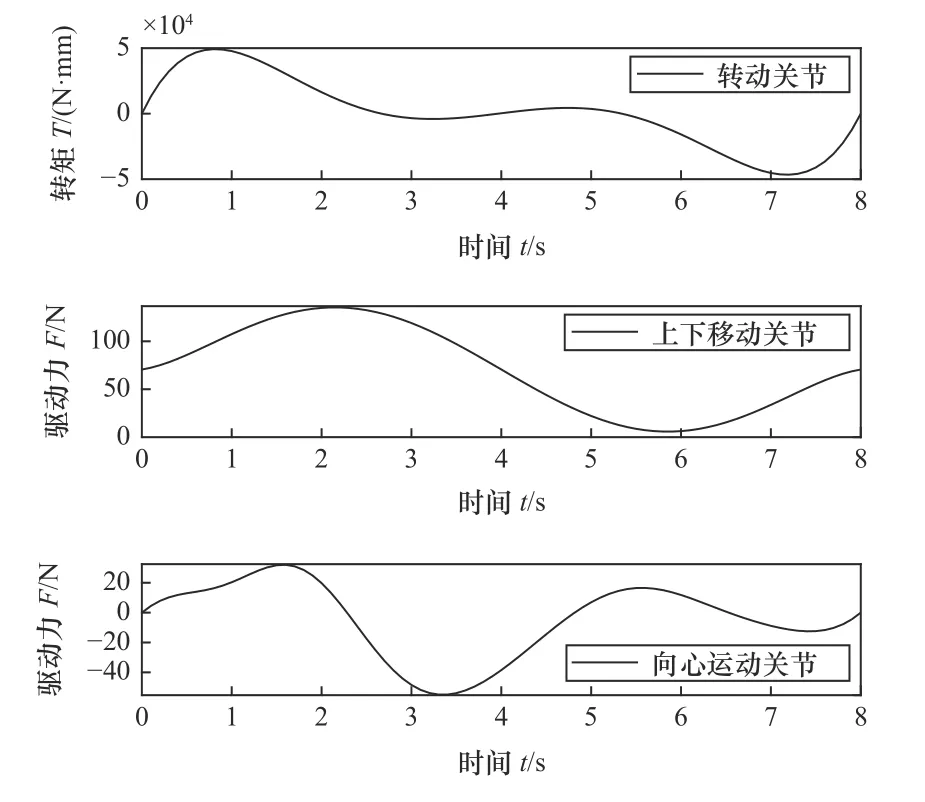
圖6 各關節隨時間變化力曲線

從圖6 中可知，整個設備在空載狀態下，轉動關節、上下運動關節和向心運動關節分別對應的轉矩和驅動力隨時間變化沒有明顯的跳變點，且各關節對應的驅動力與轉矩數值隨時間呈現規律性變化[23]。

2.5 仿真實驗

新型固定式割膠機在切割時，膠刀會受到3 個方向的作用力如圖7 所示，分別為F1=100 N、F2=100 N、F3=100 N。

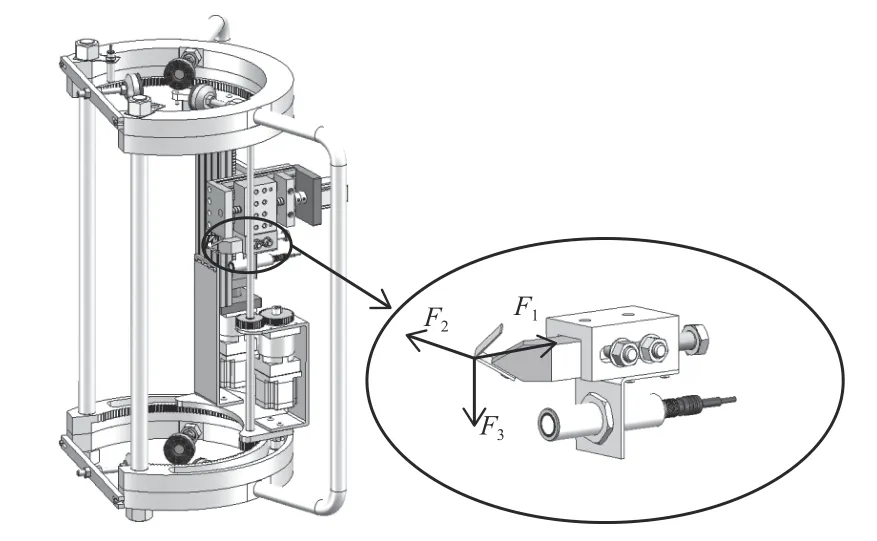
圖7 作用力示意圖

由于絲杠傳動模塊和傳動齒輪組的動力均來自于電機的輸出轉矩，因此傳動齒輪組電機驅動函數表示為STEP(time,5,0d,13,90d);絲杠傳動模塊5 電機驅動函數表示為STEP(time,5,0d,13,32d)；絲杠傳動模塊3 電機驅動函數表示為STEP(time,0,0d,5,STEP(time,5,5d,6,STEP(time,6,-0.5d,7,STEP(time,7,0.25d,8,STEP(time,8,-0.5d,9,STEP(time,9,0.75d,10,STEP(time,10,0.25d,11,STEP(time,11,0.25d,12,-0.5d))))))))。由此可得如圖8 所示的曲線圖。

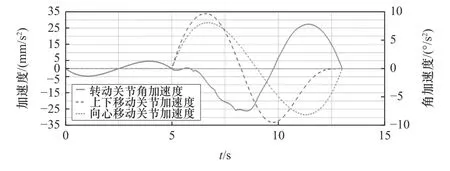
圖8 各關節加速度曲線圖

由圖8 可以看出，0～5 s 向心運動關節先帶動膠刀移動到樹皮表面，5～13 s 各關節聯動完成割膠工作。整個設備在負載情況下，轉動關節和上下移動關節均為單向運動，其加速度曲線呈正弦函數變化。由于樹皮表面粗糙，向心運動關節需要快速頻發往復運動，其加速度曲線呈無規律變化。綜上所述，基于RPP 串聯機構的固定式割膠機在切割運動中具有良好的穩定性。

3 結語

（1）基于仿生學設計了一種新型固定式割膠機。將人工割膠過程分解為3 個運動，通過齒輪以及絲杠傳動疊加實現割線軌跡，并通過膠刀實現沿割線軌跡切割樹皮。

（2）采用機器人理論對割膠機進行理論模型的構建，并以此為基礎進行運動學以及動力學求解，為新型固定式割膠機的運動控制提供理論依據。

（3）基于RPP 串聯機構的固定式割膠機虛擬樣機在模擬負載條件下，加速度無明顯跳變，因此具有較好的平順性，對實物研發提供正向參考價值。