雙曲面型離子阱極桿精密車削方法＊

李佳偉 吉 方 趙 舜

（中國工程物理研究院機械制造工藝研究所，四川 綿陽 621900）

線性離子阱是質譜儀中關鍵核心部件，由兩組雙曲線形級桿組成，如圖1 所示。由于離子是限制在二維軸線上，因此極桿的長度決定了質譜儀的存儲容量；極桿非光滑表面或非理想的雙曲面輪廓將在離子激發中引入了高階場，使被激發的離子脫離共振，同時還會影響其峰值軸向俘獲勢以及離子云的分辨率[1-3]。因此，極桿的幾何輪廓和表面質量直接影響了離子阱的性能指標。雙曲面型級桿具有非回轉對稱截面形狀，同時又是典型的細長桿弱剛性結構，采用常規的工藝很難達到高精度雙曲面電極的制造。極桿除了本身的制造精度較高，還需要與極座相連，以保證形成相互正交的電場。為了降低對裝配精度的要求，現有的一體加工成形加工工藝方法，如采用整體裝配后精密線切割成型的工藝，但限于線切割設備的精度，難達到所需要的雙曲面輪廓精度[4-5]，同時表面的電腐蝕層也會影響表面粗糙度。而單件加工后再裝配的工藝，對極桿的尺寸精度要求就會更高。在單極桿的加工工藝方法中，Clare A T 等[6]采用基于數字激光成型的快速成型方法，利用PMMA 光敏特性制成雙曲面型基底，然后鍍上金膜。文中僅給出了極桿表面粗糙度（Ra約為430～740 nm）和試制后的離子阱性能，其幾何輪廓誤差尚未給出；吳定柱等采用成形磨削的方法[7]，幾何輪廓精度能達到3 μm，由于極桿的精度是砂輪輪廓精度的復印，因此極桿精度的進一步提高受限于砂輪的修整精度。綜上所述，要同時實現雙曲面光滑表面和高精度的輪廓精度，現有的制造工藝都存在一定問題。

圖1 雙曲面型離子阱及其形成的正交電場

采用多軸車床可以實現非圓截面的車削加工，筆者曾在具有C/X/Y/Z軸的車銑復合加工中心上實現了非回轉對稱截面恒定車削角度的車削加工[8]，但其C軸伺服響應遠達不到高精度曲面制造的要求。隨著多軸伺服技術的發展以及PVT（位置-速度-時間）樣條插補技術的應用，慢刀伺服車削技術在離軸非球面等非對稱曲面的加工中可以實現高精度的極光順車削，不過基本以端面車削為主。王貴林等人[9-10]研究了FTS（快刀伺服）加工中刀具切削角度的變化規律及刀具干涉分析，余德平等人[11]研究了用于非圓截面的變C軸轉速的軌跡生成方法，用以降低伺服跟蹤誤差。

本文擬采用慢刀伺服車削的加工工藝方法，雙曲面極桿進行了加工試制。

1 雙曲面極桿加工工藝分析

試制的極桿整體外形為柱狀，見圖2，截面曲線由圓弧曲線和雙曲線組成，圓弧曲線所形成的柱面為與極座的安裝定位面，工件的設計中心為圓弧的圓心。雙曲線標準方程為x2-y2=a2，在設計坐標系的方程可寫成

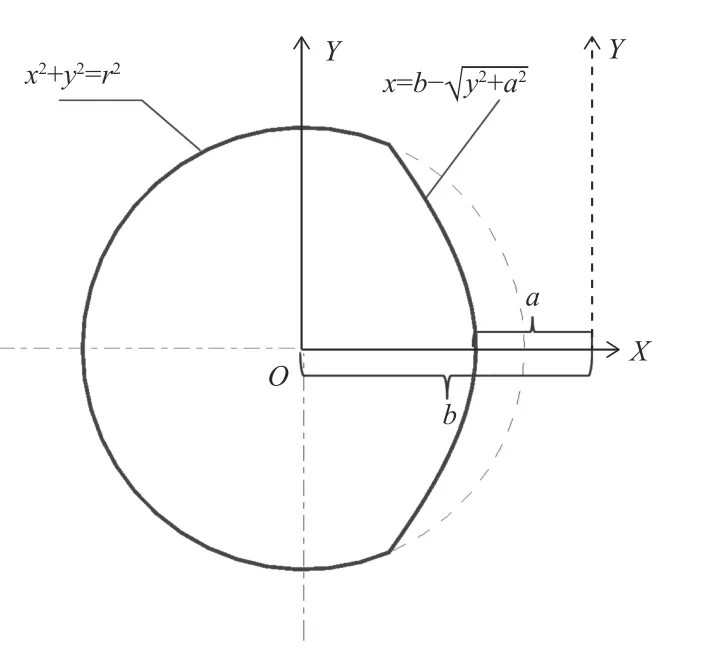
圖2 擬試制的雙曲面型極桿截面示意圖

該雙曲線的漸近線為y=x，a為雙曲線頂點曲率半徑，參數b用來控制設計坐標系中雙曲線的離軸量。該試制極桿雙曲面型輪廓精度要求為亞微米，極桿長徑比大于10，屬于弱剛性細長桿，因此加工難度非常大。

慢刀伺服加工原理是通過將主軸運動由速度控制改為位置控制，利用C/X/Z三軸聯動可在極坐標或圓柱坐標系內實現非回轉對稱曲面加工的方法[12]。因此要實現雙曲面截面的慢刀伺服車削，需要對截面輪廓形狀進行分析。同時針對細長桿的加工需求，設計特定工裝夾具，以滿足加工精度指標。

1.1 刀具附加角度分析

在非圓截面車削加工中，由于沒有Y軸或刀具旋轉軸，單個回轉周期中，刀具的實際工作角度會相對于名義工作角度發生變化，這個角度的變化稱為附加工作角度，本文用μ表示，如果附加角度過大，超過刀具的名義角度，會直接造成刀具干涉。利用車削中速度矢量的分析可以表征附加角度，如圖3 所示，假定曲線上刀觸點為P，刀具上接觸點為P′，在當前時刻，點P與P′位置重合，但是瞬時速度矢量方向不一樣，實際切削速度方向就是兩個速度的矢量差，可用下式表示：

圖3 非回轉截面車削刀具附加角度形成示意

由于刀具沿軸向（Z向）速度較小，相對于其他速度分量可忽略，近似認為刀具只沿徑向方向運動，因此有vP′=dr/dt，其中r為徑向位移，可用極坐標r(θ)表示，對應機床的X軸位置，其中θ角是時間t的函數，反映主軸的轉速。曲線上刀觸點P在做瞬時圓周運動，因此有vP=rω。這兩個速度矢量相互垂直的，刀具附加角度μ實際上就是切削速度矢量vturn與刀觸點速度矢量vP之間夾角，因此有：

一般刀具為0°前角，前刀面發生干涉的可能性較小。假定刀具名義后角為 α0，則切削狀態下刀具的實際后角為 α=α0+μ，刀具不發生后刀面干涉的情況應滿足所有位置工作后角 α ＞0， 即 α0＞max(-μ)。

圖4 表示工件圓弧中心與主軸回轉心重合狀態下5 處刀具相對于極桿的位置，很顯然位置1 所示最容易發生刀具后角干涉，對刀具后角要求最高。

圖4 試制雙曲線桿不同加工位置刀具工作角度示意

為了獲得準確的后角需求，將式(1)代入式(4)可以得到車削雙曲線截面的附加角度，繪制出不同偏置量b下附加角度關于Y軸變化規律，見圖5。其中式(1)中a=3 mm。當b=7.5 mm 時，加工坐標系與設計坐標系重合，工件回轉中心位于圓弧中心，此時刀具附加角度μ在±25°之間變化，因此刀具名義后角需滿足 α0＞25°，曲面負半軸后角要求高。隨著b值變大，回轉心偏離雙曲面，附加刀具角度逐步減少，在b=9.3 mm時達到最小，刀具名義后角僅需 α0＞10°。此時偏心距離為9.3-7.5=1.8 mm。繼續增加偏置量b，Y正半軸刀具后角需求變高。基于上述分析，合理的偏心裝夾能解決車削雙曲面所產生較大的后角需求。

圖5 雙曲線偏心量與附加角度關系

1.2 車削軌跡設計

為了獲得較為平順的加工軌跡曲線，需要基于加工輪廓進行空行程設計，雙曲線截面車削加工軌跡優化后見圖6，將整個切削路徑分為雙曲線部分和空行程部分。

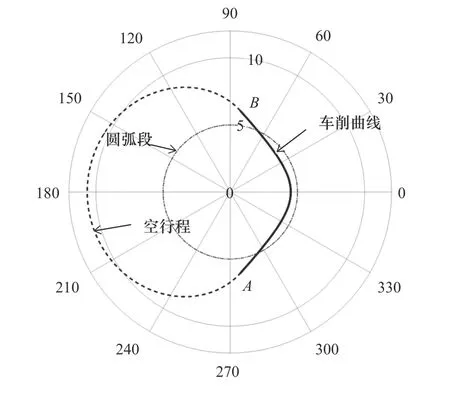
圖6 雙曲線慢刀伺服車削刀具軌跡示意圖

針對雙曲面部分，首先要把雙曲線在笛卡爾坐標的方程轉化為極坐標方程，以計算精確的加工軌跡。將x=rcosθ 及y=rsinθ 代入到式（1），可以得到雙曲面部分的極坐標方程如下：

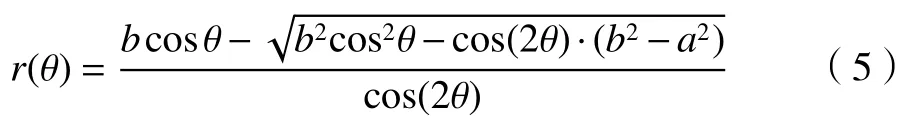
其中：θ對應主軸的方位角。在編制加工程序時，以主軸方位角 θ作為參考，計算當前的矢徑r位移（X運動軸），就可以得到慢刀伺服車削加工的離散程序點。其中主軸角度的離散增量值由插補精度決定，后續進行討論。

空行程的設計以A、B兩點為端點，并關于y軸對稱，同時須位于圓弧段范圍之外（θB＞54°）以保證雙曲線部分軌跡完整。此時空行程在A、B點處G1 連續即可，不會對加工曲面精度造成影響。把A、B兩點的矢徑（r）和矢徑關于角度的微分(dr/dθ)作為邊界條件，采用三次Hermite 插值方法，可以給出空行程的極坐標方程r(θ)，進一步對角度采樣就可以得到相位角和矢徑的數值(θ,r)進行加工程序生成。本文不做進一步分析討論。至此，單一回轉路徑的加工軌跡就完全得到了，要實現整個極桿的車削，還需要Z軸方向的進給，進給量由表面粗糙度要求決定。

2 雙曲線極桿輪廓度精度控制

2.1 加工工藝誤差分析

對柱狀截面進行車削時，由于整個切削過程刀具接觸點不會發生變化，因此刀具形貌誤差不影響工件輪廓精度。假定機床嚴格按照給定的數控代碼運動，那么最終影響加工輪廓誤差的因素就是程序本身的離散誤差和刀具對刀誤差。實際上，由于伺服運動還存在跟隨誤差，這個值與機床各運動軸的速度、加速度有關，文獻[11]中利用變轉速采樣降低加速度來降低伺服跟隨誤差，結果顯示變主軸轉速車削相比定主軸轉速車削確實能提高輪廓精度，因此本文中就不再進行分析。綜上，本文主要從程序離散誤差和刀具對刀誤差兩個方面對輪廓精度的影響進行分析。

（1）程序點離散誤差分析

由于數控程序是離散點采樣，采樣點之間軌跡相對于理論輪廓的偏差為離散誤差。慢刀伺服切削采用PVT（位置-速度-時間）插補，其底層為Hermite插值，具有G2 連續的特點，光順性好，可保證在一定擬合誤差的基礎上降低采樣點數量。即在相同的采樣數量下，相比直線插補能降低離散誤差。如圖7 所示，通過計算，按等角度采樣，當角度采樣間隔為5°時，徑向最大偏差小于0.05 μm（實際雙曲面的角度范圍在60°以內），采用該工藝參數能夠滿足加工的精度需求。

圖7 PVT 插補輪廓擬合徑向偏差誤差（C 軸增量5°）

（2）刀具對刀誤差對輪廓精度的影響

刀具對刀誤差是指刀位點坐標偏離實際機床坐標值的誤差，在本加工實例中，刀觸點不變，因此刀位點為刀觸點。刀具對刀誤差對應到機床X/Y方向上，分別用徑向誤差 Δr和高度誤差 Δh兩個值表示，對刀誤差將導致真實輪廓偏離理論輪廓。

根據雙曲線式（1），如圖8 所示，輪廓偏差定義為

圖8 對刀誤差對雙曲線輪廓影響示意

其中

y0和x0是 理想雙曲線上的坐標值，因此θ=tan-1(y0/x0)。將式（7）和（8）代入（6）得到

不帶基準的輪廓偏差可計算如下：

表1 為不同刀具誤差組合仿真計算得到的輪廓偏差。對比1、2、3、4 這4 組數據，可以看刀具誤差的正負偏差對輪廓偏差基本無影響；對比5、6、7、8 這4 組數據，可以看出輪廓偏差對刀具高度誤差比較敏感；從第7、8 組數據還可以看出，若要曲線輪廓度控制在亞微米，刀具兩個方向的誤差應控制在2 μm 以下。考慮到加工中還存在其他的工藝誤差，因此有必要將刀具的對刀誤差控制在1 μm 以下。對刀誤差所引起的輪廓誤差形狀見圖9，通過對輪廓誤差形狀的分析可以對刀具對刀誤差進行反推。

圖9 不同刀具誤差組合形成的輪廓誤差形狀

表1 不同刀具對刀誤差組合對雙曲線輪廓影響 μm

2.2 測量誤差分析

由于雙曲面型輪廓精度較高，采用泰勒-霍布森PGI 輪廓儀進行誤差評估。不同于回轉對稱零件的測量，如果測量路徑與雙曲線桿未對齊，則會引入一定的測量誤差。如圖10 所示，正確的雙曲線測量軌跡應該為實線，如果工件擺放的位置（軸線）與測量路徑不垂直，存在一定的偏轉角度 α，則測量軌跡就變成了虛線，此時測量軌跡的方程就會變成如下形式：

圖10 輪廓儀測量雙曲面引入測量誤差示意圖

通過仿真計算，當 α分別取0.5°和1°時，測量所引入的誤差將分別達到0.15 μm和0.58 μm。顯然，這種測量引入的誤差是不可忽略的，必須對工件方位進行校準，首先應該將偏轉角度 α準確校準出來。利用輪廓儀自動找最高點的方法可以記錄當前截面的最高點位置X值；然后將工作臺的Y軸移動一定距離L，執行相同的步驟以找到此刻截面的最高點，記錄下新X值，兩個位置的X的差值記為 Δx，偏轉角度可以從下式給出：

3 雙曲面極桿加工實例

本實驗在超精密機床上進行車削試制，工件材料為316 不銹鋼基體鍍鎳，圓柱名義尺寸為Φ10 mm，長度105 mm。機床直線軸精度小于0.5 μm/全行程，C軸定位精度為±2″。加工時的工位布局見圖11，所使用刀具為單晶金剛石，刀具名義前角為0°，名義后角為15°，刀尖圓弧半徑為1 mm。為了實現弱剛性極桿的車削加工，因此設計了用于增強剛性的保持架，極桿與保持架之前采用M3 螺釘進行緊固。同時為了避免刀具后角干涉，保持架上的安裝定位面的軸線與回轉軸線之前有1.8 mm的偏移，分析過程見圖11。切削時的工藝參數見表2。

表2 加工工藝參數

圖11 雙曲面桿車削過程與加工實物

為了消除刀具對刀誤差，在正式加工前使用對刀件進行了端面和外圓的車削。刀具高度誤差會在車削端面的中心殘留圓柱或圓錐，利用顯微鏡和刀座微調機構可用于高度誤差的消除，直至圓柱或圓錐消失；利用Zeiss 三坐標（精度0.5 μm）對車削的外圓尺寸進行計量可以消除徑向誤差。通過上述方法，兩個方向的誤差可以控制在1 μm 內。測量工位見圖12，利用多軸微調平臺將極桿軸線調整至與輪廓儀X軸垂直，否則會引入測量誤差。精密對刀前測量數據見圖13a，pv值為2.54 μm。程序補償后對整段進行車削加工，測量時沿軸向105 mm上截取9 個截面，每個截面間隔約10 mm，獲得的輪廓誤差數據見表3，pv值基本穩定在0.3 μm 左右，其中第8 個截面的誤差輪廓見圖13b。沿周向測得的表面粗糙度見圖13c，Ra 為13 nm。

表3 精加工后不同截面輪廓儀計量結果

圖12 輪廓儀測量工位

圖13 雙曲面輪廓儀測量結果

4 結語

本文系統地介紹了雙曲線極桿的車削加工工藝，驗證了加工工藝方法，實現了線輪廓0.3 μm 及表面粗糙度13 nm的極桿試制。本文對刀具附加角度、加工誤差和測量誤差進行了研究和分析。

（1）刀具干涉是非圓截面車削中一個關鍵問題，為了選擇正確的刀具，需要先進行刀具附加角度的計算；分析表明，合理的偏心裝夾可以降低對大刀具后角的要求。在本項目中，如果偏心夾緊，刀具后角的要求可以從25°降至10°。

（2）刀具對刀誤差對輪廓誤差影響較大，2 μm刀具徑向誤差可導致0.56 μm 輪廓誤差。此外，刀具徑向誤差不僅會在刀具對刀過程中引入，加工中的系統的溫度偏移也會引起對刀誤差，需進行關注。

（3）與回轉對稱零件的測量不同，雙曲線桿與輪廓儀測量路徑的失斜會引入測量誤差，應通過多軸運動平臺進行校準并消除。

在今后的工作中，極桿的加工效率需要進一步考慮。可進行多工位夾具的設計，一次裝夾實現多根極桿的制造，需要對夾具設計和車削軌跡進行分析和優化。