大尺寸球形件的光筆式視覺測量系統設計＊

蔣靈搏 李云雷

（①山東工業職業學院，山東 淄博 256414；②山東理工大學機械工程學院，山東 淄博 255049）

球形結構的零件在航空航天裝備、機械制造和精密儀器儀表等領域應用廣泛，如航空發動機的角接觸球軸承、硬密封球閥、球形鉸鏈和球形曲柄曲軸等[1-3]。在某些特殊工業生產過程中，大尺寸的球形或非整形球面特征的零件也有較大需求，如高壓天然氣輸送管道的球閥[4-5]，其直徑約在100～1 016 mm；制造天線球面屏的大型球面模胎，其曲率半徑可達12.8 m[6]。針對不同尺寸的球形零件，球徑和球度誤差的測量評定是進行產品質量控制的重要手段。

目前，球形零件的測量設備主要包括三坐標測量機、氣動量儀、激光干涉儀以及激光跟蹤儀等[7-8]。這些設備用于大尺寸的球形零件測量時，仍存在不足之處。三坐標測量機工作于實驗室環境，無法應用于工業現場，其測頭只能沿3 個坐標軸方向移動，自由度有限，受自身結構和測頭長度制約，無法探測大尺寸整球面的底部區域，存在測量盲區，并且維護成本高。氣動量儀和激光干涉儀僅適用于小尺寸球形構件的測量。激光跟蹤儀可實現高精度大范圍的三維點測量，但其價格昂貴，并且易受環境溫度、壓力等因素的影響。

綜合上述問題，本文設計了一種光筆式視覺測量系統用于大尺寸球形零件的測量。在攝像機視場范圍內，系統自帶的光筆可以在三維空間內自由移動，光筆的針狀測頭能夠探測到球形零件表面的任意點，并快速生成測點的三維坐標，進而擬合出理想球，計算獲得球徑和球度誤差。

1 系統工作原理

光筆式視覺測量系統主要由攝像機、光筆和配套的圖像處理軟件組成，其工作原理如圖1 所示。攝像機的空間位置固定，其坐標系為OC-XCYCZC，原點OC位于攝像機的光心。光筆上分布有共面的控制點，其自身坐標系為OP-XPYPZP，原點OP位于右下角的控制點處。

圖1 光筆式視覺測量系統的工作原理

測量時，手持光筆在攝像機的視場范圍內自由移動，光筆測頭接觸球形件表面的任意點，每接觸一點拍攝一張像片，并保證像片內含有全部的控制點。利用圖像處理軟件提取出像片中每個控制點的像素坐標，它們在光筆坐標系的三維坐標已知，進而計算出光筆坐標系和攝像機坐標系之間的位姿關系，即旋轉矩陣RPC和平移矢量TPC。假設光筆測頭在自身坐標系OP-XPYPZP的坐標為 (XPh，YPh，ZPh)，則它在攝像機坐標系的坐標為

實際上， (XCh，YCh，ZCh)就是光筆測頭接觸的球面被測點在攝像機坐標系下的三維坐標。光筆測頭每接觸一點，分別對應不同的旋轉矩陣RPC和平移矢量TPC，依據式（1）就可以計算出球面上所有被測點在攝像機坐標系下的三維坐標。

2 光筆設計

2.1 光筆結構

為了有效探測大尺寸球形零件表面的三維點，光筆設計成圖2 所示的結構，包括定向棋盤格、金屬測桿和針狀探頭三部分。定向棋盤格粘貼于平面精度等級較高的亞克力透明板上，保證所有角點共面，光筆坐標系原點OP位于圖2 所示的角點位置，XP軸 沿水平方向，YP軸沿豎直方向，ZP軸按右手法則確定，每個小方格（包括黑色和白色）的尺寸為28.4 mm×28.4 mm，從而計算出所有角點在光筆坐標系的三維坐標，其ZP坐標均為0。金屬測桿用于擴展測量范圍，可以依據被測對象幾何尺寸大小定制不同長度的測桿。針狀測頭與測桿螺紋連接，與球面三維點形成點接觸，避免了球形測頭產生的半徑補償誤差。

圖2 光筆結構

2.2 光筆標定

光筆標定是確定針狀測頭在光筆自身坐標系OP-XPYPZP的精確三維坐標。本文采用近景攝影測量方法[9-10]實現光筆標定，如圖3 所示，手持攝像機從多個角度拍攝光筆的9 張像片，要求每張像片均包含完整的光筆圖像。

圖3 光筆的近景攝影測量

光筆標定的具體步驟如下：首先，在9 張像片內提取針狀測頭和圖2 虛框內全部角點的像素坐標，并對每張像片提取的像素坐標進行匹配（按相同順序排列）；其次，根據所有角點在光筆坐標系內已知的三維坐標和它們在每張像片的像素坐標，可以建立每個攝像機（亦稱攝站）坐標系和光筆坐標系之間的轉換關系（轉換原理參考本文章節3），也就確定了所有攝站的空間位姿；最后，采用近景攝影測量中的光束平差算法，求出光筆的針狀測頭在其自身坐標系OP-XPYPZP的精確三維坐標，結果為（-200.328 mm，91.430 mm，-12.531 mm）。所有攝站的位姿和角點以及測頭的空間分布，如圖4 所示。

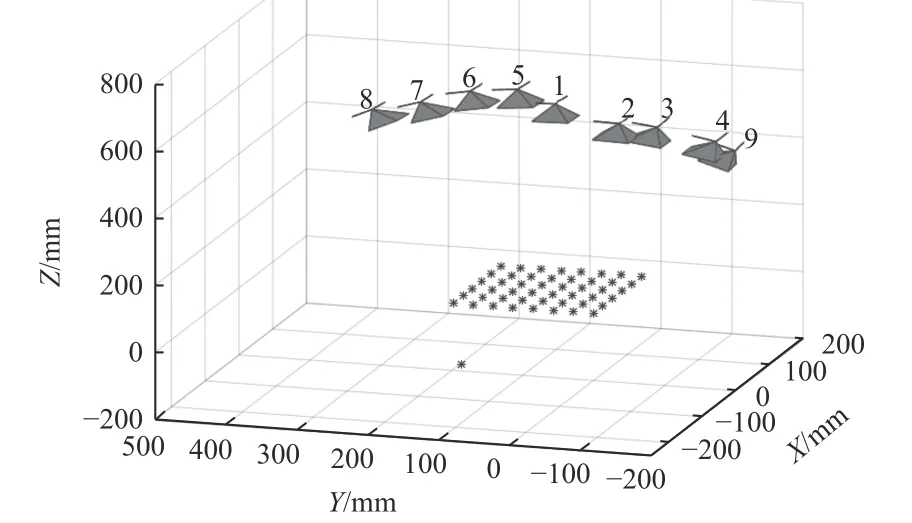
圖4 攝站位姿和角點、測頭的空間分布

3 坐標系的轉換

在圖1 中，要獲得被測點在攝像機坐標系的三維坐標，關鍵是建立光筆坐標系和攝像機坐標系之間的位置關系，即計算出旋轉矩陣RPC和平移矢量TPC。如圖5 所示，物方平面是光筆棋盤格所處平面，任意控制點（即角點）為Mi，它們在像平面的像點為mi，坐標系轉換的具體步驟如下：

圖5 坐標系的轉換原理

（1）像點的像素坐標轉換至攝像機坐標系，并歸一化處理。設像點的像素坐標為mi=[xi,yi]T(i=1,2,···,n)，并假設已對mi做了畸變矯正處理。再令攝像機的內參數矩陣為：

其中：fx、fy為 攝像機的主距，cx、cy為攝像機的主點坐標。

將像點mi轉換至攝像機坐標系，并以主距為單位做歸一化處理。令轉換后的歸一化坐標為則有

（2）構建物方平面與像平面之間的單應性矩陣。令控制點Mi在光筆坐標系的齊次坐標為=[Xi,Yi,0,1]T，則有

其中：λ為非零的比例系數。將旋轉矩陣RPC的第i列元素表示ri，則式（4）演變為

n組對應點列寫出 2n個線性方程，構建目標函數，采用Levenberg-Marquardt（LM）算法進行非線性優化求解，最終獲得H的最佳近似解。

（3）確定RPC和TPC的近似解。將單應性矩陣以三個列向量的形式表達，即H=則旋轉矩陣RPC的列向量和平移矢量TPC的計算公式為：

其中：“ ||” 代表向量的模，“ ×”代表向量的叉積。

（4）確定RPC和TPC的最優解。構造如下的目標函數

(K,RPC,TPC,Mi)是 物方平面控制點Mi依據近似的RPC、TPC和攝像機內參數矩陣K在像平面的重投影像素坐標，mi則是實際提取的像素坐標。式（7）是一個非線性最小化問題，代入RPC和TPC的近似解，再利用LM 算法獲得它們的最優解。

4 實驗

4.1 精度評價實驗

本文選取高精度的光柵尺評價光筆式視覺測量系統的測量精度，光柵尺在1.0 m的行程范圍內測量誤差優于5 μm。實驗設備包括已標定的攝像機（尼康D3200）、光筆、光柵尺（動尺和定尺）以及數顯表。

如圖6 所示，光柵尺動尺初始位置在最右側，將數顯表調零，然后讓動尺向左移動一定距離，并由數顯表讀出，作為位移基準值。動尺頂部開有錐孔，在其移動的起點和終點，光筆分別探測錐孔尖端，以確保接觸到同一點，同時由位置固定的攝像機拍攝兩張像片，依據本文前述理論獲得錐尖移動前后的兩個三維坐標，進而計算出動尺的位移，作為光筆式視覺測量系統的測量值。實驗共選擇了3個基準值，針對每個基準值均測量5 次，測量結果如表1 所示。

表1 精度評價實驗的結果

圖6 精度評價實驗的設備

實驗中，攝像機距離光柵尺約1.8 m，視場范圍約2 000 mm×1 500 mm。表中數據表明，在上述視場范圍內，系統的相對測量精度約為0.05 mm/1.0 m，能夠滿足一般工業產品在加工制造過程中的幾何精度要求。

影響該系統測量精度的主要因素包括：攝像機標定的精度、光筆標定的精度和圖像處理過程中角點像素坐標的提取精度。通過選擇尺寸更加精確的標定板，增加像片的拍攝數量等措施，進一步提高攝像機標定和光筆標定的精度。利用Harris 角點檢測算法（精度0.03 像素）可獲得光筆中定向棋盤格角點的精確像素坐標[11]。另外，還要保證測量環境具有足夠的光照強度，以便獲得清晰的光筆像片。若環境光線較暗，可在攝像機的閃光模式下拍攝。

4.2 測量實驗

實驗設備包括直徑約為280 mm的大尺寸金屬球、攝像機（尼康D3200）和光筆。攝像機固定于三腳架上，金屬球固定于工作臺，二者距離約為1.5 m。如圖7 所示，手持光筆依次探測球的頂部和前后左右等區域，每接觸一點，攝像機拍攝一幅像片，經圖像處理后，計算出被測點在攝像機坐標系下的三維坐標。

圖7 大尺寸金屬球的測量實驗

實驗共提取金屬球表面的160 個測點，并由這些點生成最小二乘擬合球，如圖8 所示。具體數據如下：擬合球的球心坐標為（-32.632 mm，88.427 mm，1 171.249 mm），球半徑為R=140.047 mm，被測點到球心的球半徑變化區間為[139.346 mm，141.275 mm]，則金屬球的球徑誤差為1.929 mm。

圖8 提取的被測點和擬合球

5 結語

為了實現大尺寸球形件的球徑、球度誤差測量，設計了一種光筆式視覺測量系統。其中的光筆設計成點接觸形式，避免了球形測頭的半徑補償誤差，并利用近景攝影測量方法完成光筆標定。提出了利用物方平面與像平面的單應性矩陣構建光筆坐標系與攝像機坐標系之間位姿關系的方法。基于光柵尺的精度評價實驗表明，系統的相對測量精度為0.05 mm/1.0 m。同時，針對大尺寸金屬球實現了球徑和球度誤差測量。