閉合Fe-Si結構中磁致伸縮引起的機械共振研究

李勁松 梁振宗 孫英倫 李國鋒 余恪平

閉合Fe-Si結構中磁致伸縮引起的機械共振研究

李勁松1梁振宗1孫英倫1李國鋒1余恪平2

（1. 大連理工大學電氣工程學院 大連 116024 2. 全球信息與通訊研究所（早稻田大學） 東京 169-8050）

降低電力變壓器和電機產生的有害噪聲一直是諸多學者的研究熱點。而產生這種噪聲的振動系統很可能處于共振狀態，并使之進一步加劇，其共振源又可能來自機械力或電磁力。該文研究疊置電工鋼片結構磁致伸縮變形與機械共振之間的相互作用。對共振現象的研究，通常考慮的是驗證電磁力的頻率及空間分布與固有頻率及匹配結構振型相一致，但此次分析表明，磁致伸縮在無前述情況下也可以誘導共振，且采用冷軋晶粒取向（GO）和非晶粒取向（NO）電工鋼片構成的框型和環型兩種閉合結構證實了這一假設。針對振動位移進行有限元（FE）仿真計算和試驗測量的數據對比，并描述鐵磁性材料磁致伸縮張力引起的機械共振及相應的振動頻譜。

疊置電工鋼片 磁致伸縮變形 機械共振 振動位移 閉合結構

0 引言

通常當電氣系統在公共區域運行時，對其質量評估的一個主要考慮因素就是噪聲，且這種系統噪聲的主要來源可分為電磁源和機械源兩類。但電磁源輻射是電力變壓器和電機最典型的噪聲成分。除了導體（如繞組）中洛倫茲力的貢獻外，這些電氣設備中的電磁噪聲主要是由磁致伸縮張力（如鐵磁性材料鐵心）和麥克斯韋應力（如氣隙和接縫）引起[1-3]。因此，振動和噪聲是電氣設備的固有特性，并不能完全消除。文獻[4]指出磁致伸縮引起的電磁效應高達總電磁力的50%。這就解釋了為什么磁致伸縮仍然是電力變壓器和電機的主要噪聲源，正如文獻[5-7]研究所述。此外，采用的鐵磁性材料的磁彈性能也受到加工工藝和其他一些物理因素的影響，如軋制、熱處理、切削及機械應力等。對此，文獻[6, 8-9]提出幾種磁致伸縮特性模型來恰當描述上述情況。進一步地，文獻[10-12]將這些模型納入開發的有限元（Finite Element, FE）仿真軟件以評估電機中的磁致伸縮變形和振動。可即便如此，關于磁致伸縮與電氣設備結構振動之間的相互作用研究還是很少[13-15]，對振動問題的分析基本停留在固有頻率這一概念層面。實際上，當低阻尼結構（如電力變壓器、電機等）受到周期性力激勵時，會產生受迫振動；且當激勵頻率與結構的某個固有頻率相匹配時，將導致位移放大，繼而發生共振。每個形變的振動模態都與一個固有頻率相聯系，模態的數學表示可由采用的基礎頻率和結構振動的適當形式共同組成。

系統的動力學特性通常可用常系數、和的二階線性偏微分矩陣方程表示，即

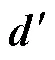
為滿足固有頻率計算中的無阻尼自由振動條件，需使式（1）中=0,=0，則無阻尼結構的自由振動方程為

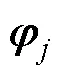
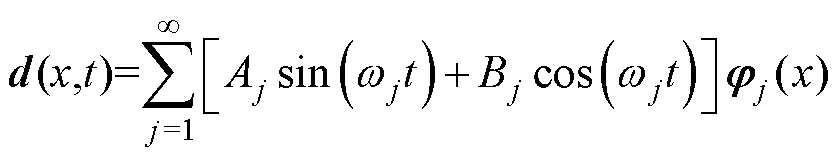
從力學分析到共振檢測，本文對磁致伸縮引起的共振現象進行了全面地研究。首先對研究所用結構進行描述；其次通過磁致伸縮張力和麥克斯韋應力計算與對比，討論建模仿真結果；再次對結構的力學性能進行完整分析，結合仿真計算和試驗測量進行結果比較；最后對磁致伸縮引起的機械共振加以詳細總結。

1 結構描述

圖1所示為研究采用的鐵磁性閉合結構。其中，圖1a所示結構可比作長寬為200mm×200mm，柱高50mm，包含50片絕緣浸漆電工鋼片，每片厚度0.30mm，總厚度為17mm的單相變壓器鐵心；圖1b所示結構也可比作內徑為150mm、外徑為200mm，由30片浸漆絕緣電工鋼片組成，每片厚度0.50mm，總厚度為16mm的單相變壓器鐵心。

圖1 研究采用的鐵磁性閉合結構

為了研究磁致伸縮變形，本文考慮了沒有搭接接縫的框型和環型疊置電工鋼片簡單組合。實際工程中鋼片在拐角處進行交疊的搭接組裝結構經常被用到，因為它始終允許磁通在材料的軋制方向上流通。但當磁力線從一片鋼片到另一片鋼片流過小的層間氣隙時將產生磁吸引力。即除了磁致伸縮振動外，還存在由于層間接縫區磁力所引起的振動[16-17]。因此，鐵磁性閉合結構被切成一片，這樣在磁通路徑上就不會有氣隙或交疊（僅代表磁致伸縮振動），如圖1c所示，為放置在水平面上的單片框型閉合結構，勵磁繞組被設置在一側柱上使鐵磁性框架磁化。框型鐵心由3%的冷軋晶粒取向（Grain Oriented, GO）電工鋼30Q140制成的；環型鐵心由3%的冷軋非晶粒取向（Non-grain Oriented, NO）電工鋼50WW800構成。表1給出了這些電工鋼的典型物理特性參數。

表1 研究所用電工鋼的典型物理特性參數

Tab.1 The typical physical property parameters of some electrical steels under study

2 磁致伸縮張力和麥克斯韋應力

當疊置鐵心處于交變磁場中磁化時，磁致伸縮張力將引起鐵心疊片的尺寸變化和振動，進而導致機械共振[15]。此外，當共振發生時，存在于氣隙和接縫中的麥克斯韋應力也可能導致更高的噪聲輻 射[18-19]。由于這些力的發生頻率與磁致伸縮相同[20]，因此很難量化麥克斯韋應力比磁致伸縮張力大或小多少。為了突顯這種差異對比性，本文對一個沒有氣隙或交疊的鐵磁性閉合框型結構進行建模與計算，麥克斯韋應力僅出現在框架的四周上，如圖2所示。這些力可能是由于漏磁場線或勵磁線圈的存在所引起的。

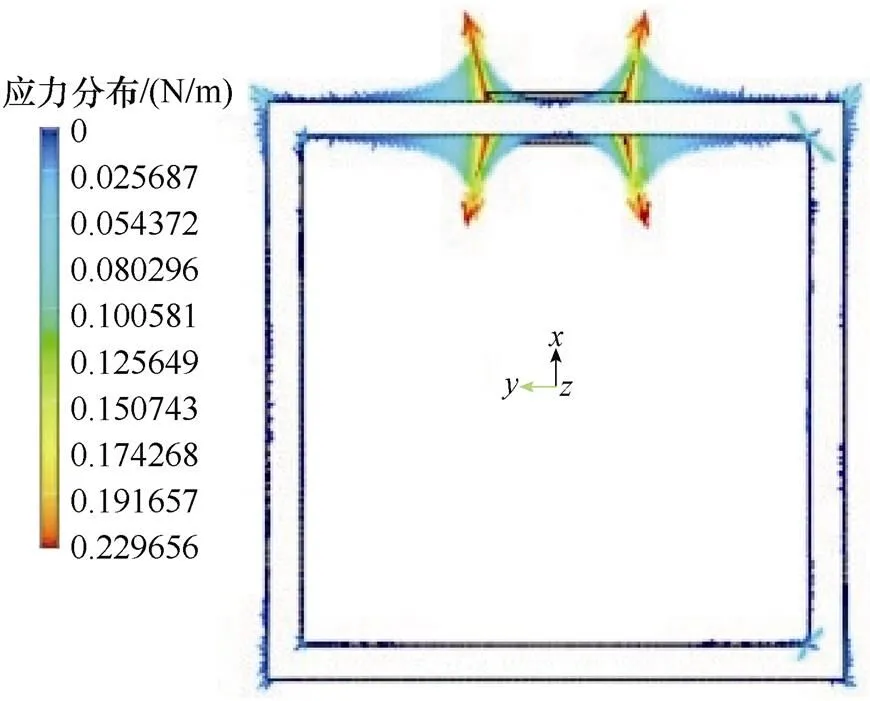
圖2 鐵磁性閉合框型鐵心的麥克斯韋應力分布仿真

麥克斯韋壓力可寫為

式中，La為漏磁場磁通密度（主要分布于框架轉角處）；0為真空磁導率，0=4p×10-7H/m。由圖2可以看出，由于周向磁通密度的量級很低，其所引起的壓力或應力也將非常弱小。

用于計算的磁致伸縮模型是基于高能和宏觀的方法，且考慮了磁性和磁致伸縮各向異性的影響[21]。提出的模型旨在最小化鐵心材料內部的自由能。總自由能tot可以寫成退磁能dem、各向異性能ani、塞曼能z和磁彈性能τ，即

tot=dem+ani+z+τ（6）

在有限元計算中，假定磁彈性耦合較弱。該方法的一般原理是在結構計算中計算網格節點的等效力，從而再現磁致伸縮變形。這些等效的磁致伸縮節點力構成結構計算中的應用載荷，并對問題的所有節點進行計算。

圖2和圖3所示為閉合框型鐵心結構的仿真結果，包括麥克斯韋應力計算和基于磁致伸縮模型的等效張力計算。經作差表明，磁致伸縮張力引起的位移是僅由麥克斯韋應力所引起位移的10倍，即ms=10Maxwell。因此，可認為磁致伸縮是引起結構機械共振的唯一來源。以往對類似變壓器結構的器件中由磁致伸縮引起的機械共振未有詳細的研究，且由于本文所設立的裝置中無氣隙，麥克斯韋應力可以忽略不計，因此可僅考慮磁致伸縮作為共振的主要來源。

圖3 鐵磁性閉合框型鐵心的位移仿真

3 鐵磁性閉合框/環架的共振頻率測定

3.1 仿真：描述與結果

3.1.1 描述（模態分析）

為了識別結構的本征模態，本文基于COMSOL Multiphysics有限元仿真軟件對鐵磁性閉合框架進行了模態計算與分析。由于閉合結構為一組疊置框型鐵心，為了盡可能地模擬真實的振動特性，所建模型為包含50片每片厚度0.30mm的鋼片組合框架（無限接近實際的框型鐵心結構），且對應地設定接觸條件（疊壓系數0.88）。利用該系數并結合表1，可以很好地模擬疊片鐵心的層間特性。為了同時獲得結構的面內和面外模態振型，在建模時將所有疊置鋼片設置為一個三維塊體集合。

3.1.2 仿真結果

鐵磁性閉合框架的振動位移仿真可分為面內振動模態和面外振動模態兩種振型。其面內位移的模態分析結果如圖4所示，面外位移的模態分析結果如圖5所示，研究的頻率范圍均為0～3kHz。

由圖4和圖5可以看出，在研究頻率范圍內，面外模態的振型比面內模態的振型更為復雜。3.1.2的有限元仿真結果將與3.2的模態試驗分析進行比較。

3.2 試驗：閉合框架的動態響應

本節研究在勵磁繞組終端無任何電激勵情況下的閉合框架結構動態特性。

首先，通過吊起鐵磁性框架，對實際的閉合結構進行測量。而后詳細介紹結構的試驗固有頻率和模態振型，如圖6所示。最后結合試驗模態和仿真模態的數值對比（見表2）進行討論。

圖6 模態振型的試驗平均頻率響應函數

由圖6可以清晰地看出，在研究頻率0～3kHz范圍內，面內和面外試驗平均頻率響應函數（Mean Frequency Response Function, MFRF）（加速度/力）都有6個共振峰，表明試驗模態振型與圖4和圖5的仿真計算結果相一致。但鐵磁性閉合框架的兩柱在如圖6b所示的面外試驗模態3～6中卻展現出一種奇怪的特性，對此現象的一種可能性判斷是與測量噪聲有關。但當旋轉框型結構1/4圈后進行第二次重復測試，原有兩柱依舊表現出上述同樣的特性。因此，可以得出結論，即在這兩柱上觀察到的局部現象與結構本身有關，也可解釋為結構內部的一些局部鋼片層脫離。總之，通過試驗可以獲得鐵磁性閉合框架的振動模態固有頻率，且面內試驗模態振型與仿真計算結果更為相似，對其所有模態頻率的預測精度也更高。表2對固有頻率的試驗值和計算值進行匯總與對比。

表2 測量與計算的固有頻率對比

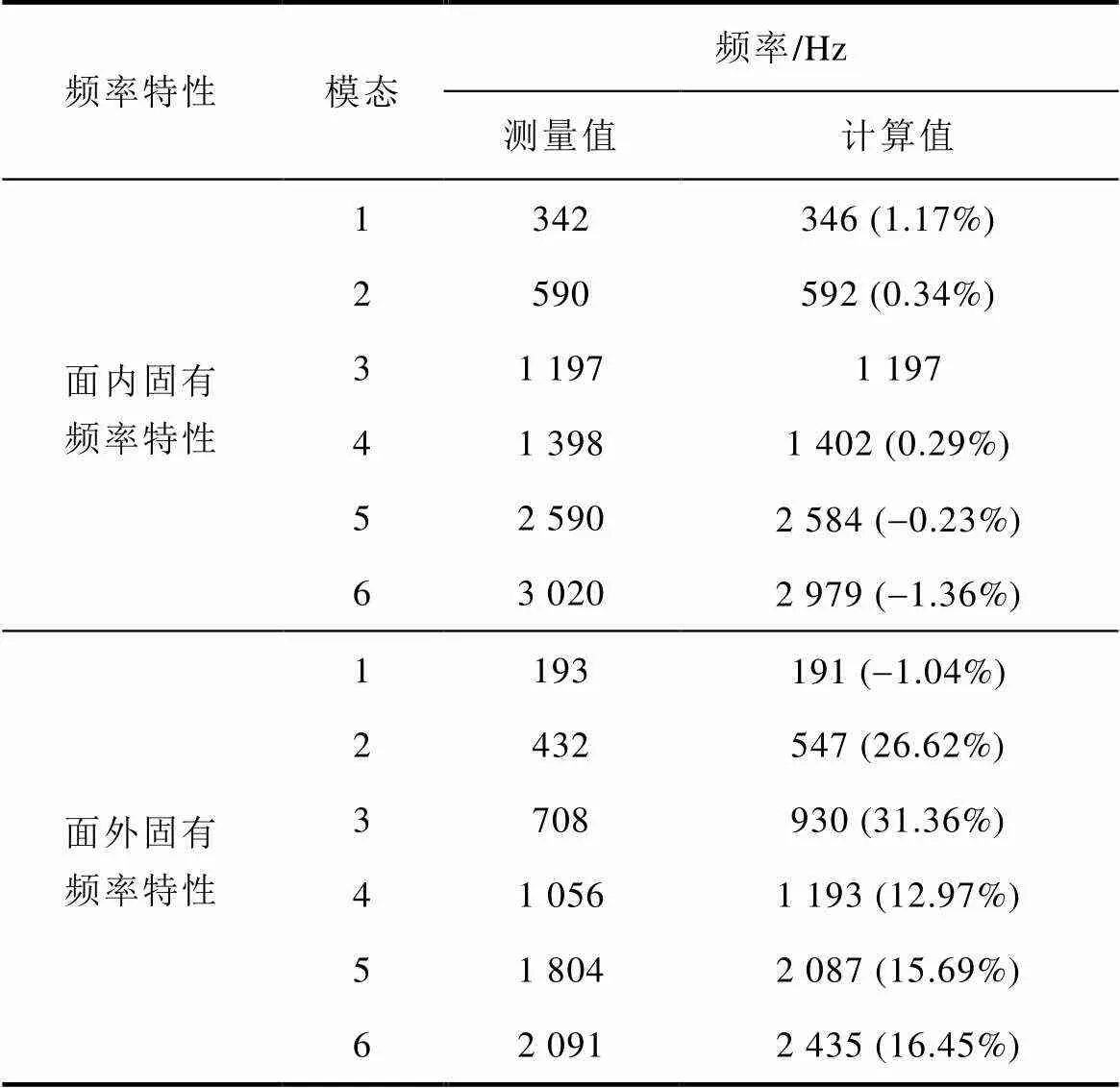
Tab.2 Comparison between measured and computed natural frequencies

對于面外模態，除一階頻率外，其試驗固有頻率與仿真結果有很大不同，但依然在可接受范圍內。因為實際的閉合疊片框架組裝結構是由絕緣漆維護的，這可能改變結構（疊片+絕緣漆）本身的機械性能。同時，由于相鄰鋼片層間的相互彈性效應以及層間絕緣漆的存在引起共振頻率的增大或減小，致使這種層間滑移結構變得更為復雜。

3.3 仿真、試驗與討論：鐵磁性閉合環架

鐵磁性閉合環架的模態振型試驗如圖7所示，和鐵磁性閉合框架的實現方法相同，同時對鐵磁性閉合環架進行了模態振型仿真計算和試驗測試。結果表明，鐵磁性閉合環架具備諸多優點：磁路縮短，減少了磁致伸縮引起的變形；閉合環架上沒有接縫，避免了接縫引起的振動和噪聲；環形結構的徑向變形將大大減小。在上述優點的共同作用下可實現一種新型的低振動、低噪聲電力變壓器鐵心設計。這將是下一步研究的重點。

圖7 鐵磁性閉合環架的模態振型試驗

4 結論

本文詳細研究了磁致伸縮張力引起的機械共振。當鐵磁性閉合框架的固有頻率與面內和面外模態振型的多重激勵頻率相匹配時，將發生結構共振。結論如下：

1）鐵磁性閉合框架的面內振動特性仿真計算和試驗測試結果相似。由于局部現象的存在，面外模態的建模與分析更為復雜。盡管如此，仿真所得頻率分辨率相對可以接受。

2）研究證實，即使在極低的激勵振幅下，僅靠磁致伸縮就可能引起疊置結構的共振。

3）當磁致伸縮張力的頻率與鐵磁性框架的固有頻率一致時，共振就會發生，而不必了解變形情況的空間分布。

4）鐵磁性閉合框架發生共振時的峰-峰值位移增大是由于面內和面外方向的磁致伸縮變形導致的。

5）鐵磁性閉合環架比鐵磁性閉合框架存在諸多更好的優點，這將是下一步研究的重點。

本文證實了磁致伸縮變形可能與疊置結構的機械共振有關，應在冷軋晶粒取向、非晶粒取向鐵磁性電工材料和任何其他等級的磁致伸縮材料設計階段就要加以考慮。為了制造運行噪聲更小的電力變壓器和電機，必須考慮由磁致伸縮引起的機械共振，它可能是噪聲的一個重要來源，并且在結構中增加阻尼是避免共振的有效方法。

[1] Peng Shuai, Jürgen B. Investigation of acoustic noise sources in medium frequency, medium voltage trans- formers[C]//2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 2014: 1-8.

[2] 陳德志, 張玉庸, 白保東, 等. 不同溫度及諧波下硅鋼片電磁-力特性與變頻電機振動[J]. 電工技術學報, 2020, 35(22): 4647-4656.

Chen Dezhi, Zhang Yuyong, Bai Baodong, et al. Electromagnetic-force and vibration of silicon steel sheet and variable frequency motor under different temperature and harmonic[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4647-4656.

[3] 翁玲, 常振, 孫英, 等. 不同磁致伸縮材料的高頻磁能損耗分析與實驗研究[J]. 電工技術學報, 2020, 35(10): 2079-2087.

Weng Ling, Chang Zhen, Sun Ying, et al. Analysis and experimental study on high frequency magneto- strictive energy loss of different magnetostrictive materials[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2079-2087.

[4] Mohammed O A, Calvert T, Mcconnell R. Coupled magnetoelastic ?nite element formulation including anisotropic reluctivity tensor and magnetostriction effects for machinery applications[J]. IEEE Transa- ctions on Magnetics, 2001, 37(5): 3388-3392.

[5] Belahcen A. Vibrations of rotating electrical machines due to magnetomechanical coupling and magneto- striction[J]. IEEE Transactions on Magnetics, 2006, 42(4): 971-974.

[6] 吳勝男, 于慎波, 佟文明, 等. 磁致伸縮引起的徑向磁通電機定子鐵心振動精確解析模型[J]. 電工技術學報, 2019, 34(2): 226-235.

Wu Shengnan, Yu Shenbo, Tong Wenming, et al. A precise analytical model of stator core vibration due to magnetostriction for radial flux motors[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 226-235.

[7] Moses A J, Anderson P I, Phophongviwat T, et al. Contribution of magnetostriction to transformer noise[C]//45th International Universities Power Engineering Conference (UPEC2010), Cardiff, UK, 2010: 1-5.

[8] Fonteyn K, Belahcen A, Kouhia R, et al. FEM for directly coupled magneto-mechanical phenomena in electrical machines[J]. IEEE Transactions on Magnetics, 2010, 46(8): 2923-2926.

[9] Aydin U, Rasilo P, Martin F, et al. Magneto- mechanical modeling of electrical steel sheets[J]. Journal of Magnetism and Magnetic Materials, 2017, 439: 82-90.

[10] 潘超, 衣雙園, 蔡國偉, 等. 交直流混雜模式下變壓器勵磁-振動特性研究[J]. 電工技術學報, 2019, 34(18): 3788-3796.

Pan Chao, Yi Shuangyuan, Cai Guowei, et al. Excitation-vibration characteristics of transformer in AC-DC hybrid operation[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3788-3796.

[11] Belahcen A, Singh D, Rasilo P, et al. Anisotropic and strain-dependent model of magnetostriction in elec- trical steel sheets[J]. IEEE Transactions on Magnetics, 2015, 51(3): 2001204.

[12] Liu Mingyong, Hubert O, Mininger X, et al. Redu- ction of power transformer core noise generation due to magnetostriction-induced deformations using fully coupled ?nite element modeling optimization procedures[J]. IEEE Transactions on Magnetics, 2017, 53(8): 8400511.

[13] 汪穎, 羅代軍, 肖先勇, 等. 多逆變器并網下的超高次諧振特性分析[J]. 電力系統自動化, 2020, 44(1): 192-199.

Wang Ying, Luo Daijun, Xiao Xianyong, et al. Analysis on supraharmonic resonance characteristics with integration of multiple inverters[J]. Automation of Electric Power Systems, 2020, 44(1): 192-199.

[14] Kamimoto K, Ishibashi F, Noda S, et al. Mag- netostriction and motor vibration[J]. Electrical Engineering in Japan, 2004, 148(2): 8-13.

[15] Somkun S, Moses A J, Anderson P I. Mechanical resonance in nonoriented electrical steels induced by magnetostriction under PWM voltage excitation[J]. IEEE Transactions on Magnetics, 2008, 44(11): 4062- 4065.

[16] Weiser B, Pfützner H, Anger J. Relevance of magnetostriction and forces for the generation of audible noise of transformer cores[J]. IEEE Transa- ctions on Magnetics, 2000, 36(5): 3759-3777.

[17] 閆榮格, 趙文月, 陳俊杰, 等. 基于諧波注入的串聯電抗器的減振研究[J]. 電工技術學報, 2020, 35(16): 3445-3452.

Yan Rongge, Zhao Wenyue, Chen Junjie, et al. Research on vibration reduction of series reactor based on harmonic injection[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3445-3452.

[18] Pellerey P, Lanfranchi V, Friedrich G. Coupled numerical simulation between electromagnetic and structural models. In?uence of the supply harmonics for synchronous machine vibrations[J]. IEEE Transa- ctions on Magnetics, 2012, 48(2): 983-986.

[19] Bouayed K, Mebarek L, Lanfranchi V, et al. Noise and vibration of a power transformer under an electrical excitation[J]. Applied Acoustics, 2017, 128: 64-70.

[20] L?ftman L. Magnetostriction and its contribution to noise in a PWM inverter fed induction machine[J]. Journal De Physique IV, 1998, 8(PR2): Pr2-567-Pr2- 570.

[21] Mbengue S S, Buiron N, Lanfranchi V. An aniso- tropic model for magnetostriction and magnetization computing for noise generation in electric devices[J]. Sensors, 2016, 16(4): 553-563.

Study of Mechanical Resonance Induced by Magnetostriction in Closed Structures Based on Fe-Si

11112

（1. School of Electrical Engineering Dalian University of Technology Dalian 116024 China 2. Global Information and Telecommunication Institute Waseda University Tokyo 169-8050 Japan）

The noise produced by power transformers and electrical machines is harmful, and its reduction has always been a research hotspot. The vibration system that produces such noise is likely to be in resonance and becomes more drastic, and the resonance may be mechanical force or magnetic force. The interaction between the deformation due to magnetostriction and mechanical resonance of a structure made up of laminated steel sheets is investigated in this paper. In the study of resonance phenomena, it is usually considered that the frequency and the spatial distribution of the electromagnetic forces coincide with the natural frequency and the mode shapes of the corresponding structure. However, it is observed that the magnetostriction may induce a resonance without the aforementioned conditions. Two closed structures of frame-shaped sheet and ring-shaped sheet consisting of cold-rolled grain-oriented (GO) and non-grain oriented (NO) electrical steels are used to confirm this assumption. The finite element (FE) simulated calculations and measurements are compared for vibration displacements. The results of mechanical resonance induced by the magnetostrictive strain from ferromagnetic materials are shown, as well as the corresponding vibration spectrum.

Laminated steel sheets, magnetostrictive deformation, mechanical resonance, vibration displacements, closed structures

10.19595/j.cnki.1000-6753.tces.L90281

TM271; TM153+.3

李勁松 男，1987年生，博士，副教授，碩士生導師，研究方向為電力變壓器集電磁振動及其減振降噪與非侵入式在線檢測的數字孿生技術、功率跟蹤型混合儲能電力變壓器及其系統等。E-mail: lijingsong2019@dlut.edu.cn（通信作者）

梁振宗 男，1998年生，碩士研究生，研究方向為電力變壓器高頻電磁振動響應與噪聲分析等。E-mail: liangzhenzong@mail.dlut.edu.cn

2020-07-08

2021-01-21

山東省科技型中小企業創新能力提升工程項目（2021TSGC1408）、濟寧市重點研發計劃（2020PZJY006）、教育部產學合作協同育人項目（202102449010，202102531001，202101109001）、中央高校基本科研業務費（DUT20RC(3)018）、國家自然科學基金青年科學基金（51807106）和日本科學促進協會（JSPS）贈款資助科學研究（KAKENHI）（JP18K18044）資助。

（編輯 崔文靜）