金屬材料層裂再壓實的模擬研究*

劉 軍，孫致遠，張鳳國，王 裴,2

（1. 北京應用物理與計算數學研究所，北京 100094；2. 北京大學應用物理與技術研究中心，北京 100871）

激波在金屬自由面卸載后，金屬材料內部可能會產生層裂（或微層裂）現象。根據激波加載強度、波形、演化時間以及金屬材料物性等的不同，金屬層裂區內部會形成層裂片、孔洞等不同的拉伸稀疏狀態。當金屬層裂區后方再次受到加載波或慣性聚心等作用時，金屬層裂區會被密實基體持續追趕并再次壓實為密實狀態，直至處于拉伸狀態的物質全部被壓實后金屬層裂區消失。該過程即為本文中所述的“金屬層裂區的再壓實過程”。

在實驗觀測上，金屬層裂區的再壓實過程體現為自由面測速曲線在首次沖擊起跳后經過一定時間間隔的二次起跳行為。而且由于不同位置上二次加載波到達時刻與多種因素相關，實驗上難以確定層裂區進入再壓實的時刻，僅能確定層裂區再壓實的完成時刻（即速度二次起跳時刻）。目前實驗在層裂區拉伸狀態及再壓實后物質狀態的精確測量上仍存在較大難度。在理論研究中，金屬層裂過程一般認為是材料內部孔洞產生、演化發展及匯合的過程。當孔洞演化到一定時間后，相互貫通形成層裂片。相關模擬研究表明，大的層裂片內部也可能存在未貫通的小孔洞。由此來看，金屬層裂區內部的拉伸狀態可能是孔洞、層裂片或兩者共存的狀態，其是隨時間變化的。在層裂區進入再壓實過程的初始時刻難以確定情況下，很難對金屬層裂區的初始拉伸狀態進行準確預測。正是由于進入再壓實階段的初始拉伸狀態的復雜性及再壓實后狀態的不確定性，宏觀模擬結果與少數實驗結果能夠較好比對，尤其難以驗證很多復雜加載下宏觀模擬該過程的可靠性，制約了金屬層裂區再壓實過程的深入研究。

在無法確定層裂區初始拉伸狀態及再壓實狀態的情況下，本文中首先將層裂區初始含有不同拉伸狀態的因素引入該問題，并通過直接模擬得到不同拉伸狀態下的再壓實狀態。然后，開展與直接模擬中工況完全對應的宏觀模擬，從而保證直接模擬與宏觀模擬具有可比性。最后，通過與對應工況下直接模擬結果對比，對宏觀精細模擬此類問題的正確性和適應性進行討論。

1 金屬斷裂再壓實的動力學過程

基于宏觀實驗診斷結果及微介觀分子動力學模擬總結，本文中將強沖擊條件下金屬層裂再壓實的力學行為分為如下6 個典型過程（見圖1）：①材料在稀疏波作用下的拉伸稀疏過程；②材料內部微孔洞增長過程；③大孔洞貫通后，含真空間隙層裂片形成的過程；④二次加載作用下大層裂片的閉合過程；⑤層裂片閉合后形成的含孔洞物質再壓實過程；⑥壓縮成密實材料后的力學行為演化過程。需要說明的是，雖然本文中將材料層裂再壓實過程的時間序列簡化為6 個過程，但真實情況下上述幾個過程間的轉換并不是序列化完成的，過程之間存在弛豫、交疊，例如：若無二次加載，則上述過程簡化為①→② 或①→②→③；若二次加載時間間隔較短，則材料內部孔洞匯合形成層裂片過程可能無法完成，斷裂再壓實過程變為①→②→⑤→⑥（目前某些孔洞增長模型中考慮了孔洞縮小因素，則該過程亦可認為是①→②）；若二次加載時間間隔較長，層裂區發展較充分，在受到一個較強的二次加載后上述6 個過程全部發生；若金屬在熔化狀態下形成微層裂現象，拉伸區充分發展后主要以金屬小液滴形式存在，上述描述過程不適用。

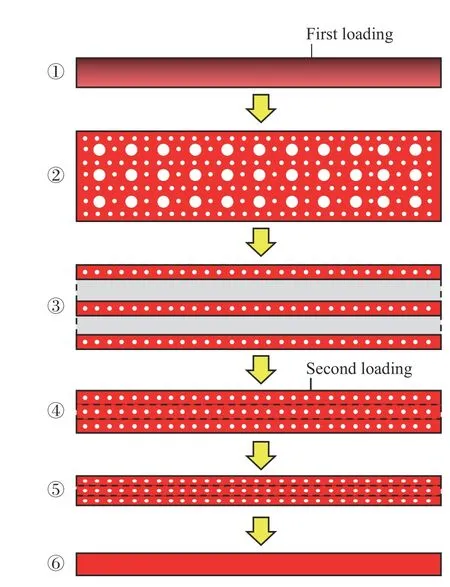
圖1 金屬層斷裂再壓實力學過程示意圖Fig. 1 Schematic diagram of the mechanical process of metal spallation and recompression

典型的①→②過程在實驗測試診斷中表現為自由面速度由最高點回落及回落速率變化等。宏觀模擬①→②過程的計算，可使用損傷模型計算孔隙度 α 。考慮其對材料狀態方程、強度的影響，重新計算得到該過程材料壓力、溫度等信息。具體形式如下：

典型的①→②過程在實驗測試診斷中表現為自由面速度由最高點回落到一定高度后再次起跳（層裂片信號）。宏觀模擬②→③過程的計算，則涉及損傷模型參數之外的另一個重要參數：截斷損傷度。隨著材料損傷度的增長，當＞情況下，認為網格內部大孔洞貫通導致含真空間隙層裂片形成。該過程計算方式可采用如下形式：

上述過程在單次沖擊金屬層裂行為模擬研究中已取得較好效果，能夠實現對單次沖擊層裂現象的模擬預測（如自由面速度、層裂片厚度等）。

典型的③→⑥過程在實驗中表現為界面速度平臺及二次起跳過程。由于相關物理量的實驗測試診斷存在困難，目前很少有針對③→⑥全過程的深入研究。這就使金屬層裂再壓實過程的宏觀模擬存在一些難以驗證的問題。首先，目前針對該過程的壓力計算處理方法種類較多：直接使用金屬負壓段EOS 處理該過程；有些則在壓實前全程設置零壓；還有的借鑒使用多孔介質的相應物理建模方法。但對于在特定工況下哪種處理更合理并沒有較明確的認識。而且，針對該過程網格溫度的計算處理方法也是沒有相關文獻進行闡述。其次，在缺乏有效驗證手段情況下，難以對該過程的密度變化、再壓實狀態等是否正確做出明確的判斷。下面通過對幾種典型拉伸狀態下層裂區再壓實的直接模擬，對上述兩點在宏觀模擬此類問題中的正確性及適應性進行討論。

2 金屬層裂再壓實過程的直接數值模擬

考慮到金屬層裂區初始進入再壓實過程（③→④過程）真實拉伸狀態的復雜性，在假設層裂片/孔洞的大小、間隙相等情況下，本節將該初始拉伸狀態分為僅含層裂片、僅含孔洞、同時存在孔洞與層裂片3 類典型情況（見圖2），使用歐拉方法進行建模和直接模擬。圖2 中 α為層裂區初始孔隙度，為層裂區單位長度上的貫通層裂片數量，為層裂區單位長度上的孔洞數量。

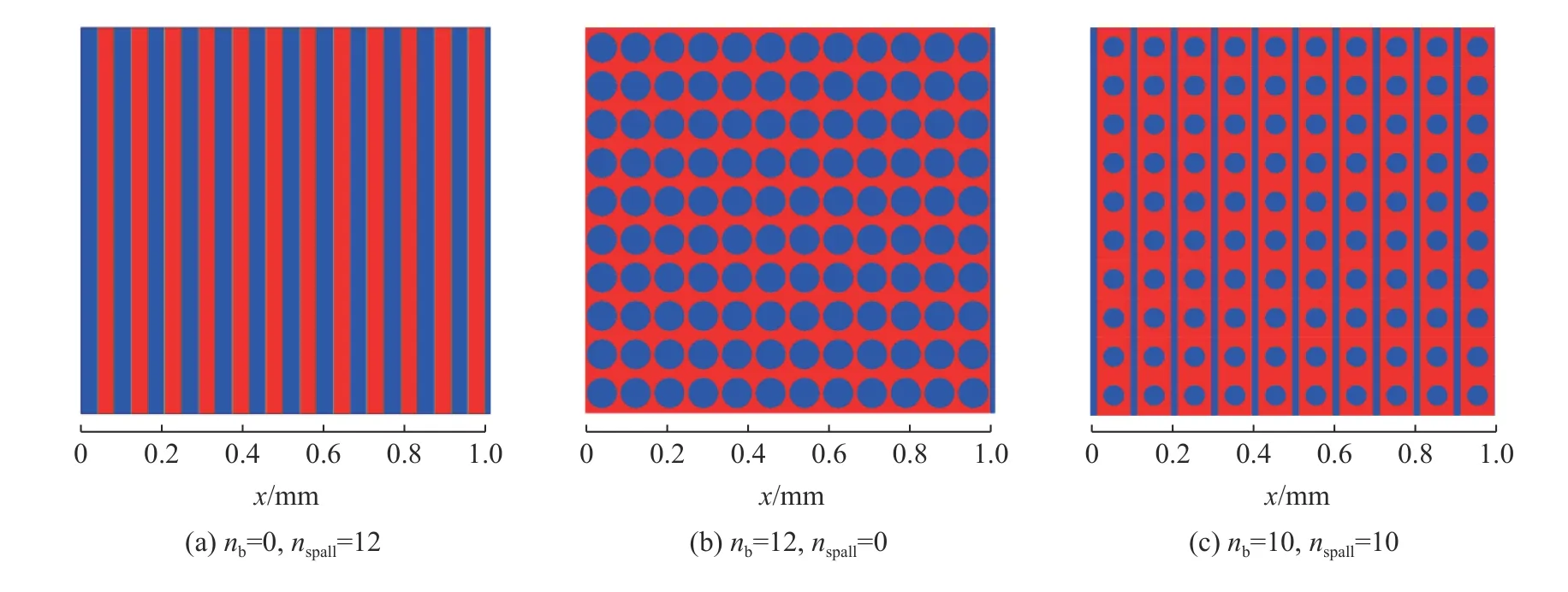
圖2 相同初始孔隙度 α0=1.3 下不同層裂區建模Fig. 2 Different models of spallation zones with the same initial porosity of α0=1.3

直接數值模擬使用自主開發的三維多介質彈塑性流體力學歐拉方法計算軟件MEPH進行計算，其中金屬使用Mie-Grüneisen 狀態方程及Steinberg-Guinan 本構模型進行計算。

對于金屬銅的計算，首先，需要驗證的是此種細觀建模情況下金屬再壓實問題直接模擬的正確性。在圖2(b)孔洞數量=12情況下 ，圖3 給出了三維多孔銅1/4 建模（該問題為純三維問題，二維軸對稱模型無法反映真實的邊界效應），計算范圍[0,1] mm×[0,0.05] mm×[0,0.05] mm，計算網格長度為 0.00125 mm，軸正方向設置為連續邊界條件、其他均設置對稱邊界條件。改變孔隙度 α、再壓實初始速率情況下，圖4 給出了8 組由MEPH 直接模擬得到的壓實密度與對應壓力（實心點）。通過與實驗結果（空心點）的對比來看，本文的直接建模模擬能夠適應考察范圍附近的含孔隙物質再壓實問題中壓實密度與壓力的模擬估計。

圖3 孔洞數量 nb=12 下的三維多孔銅1/4 模型Fig. 3 Three-dimensional 1/4 model of porous copper with nb=12

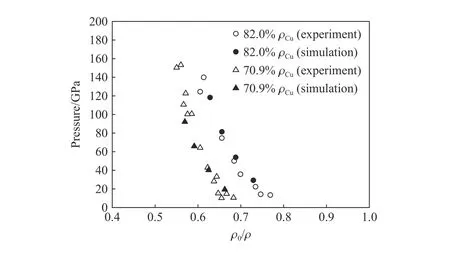
圖4 不同孔隙度下多孔銅三維直接模擬與實驗結果對比Fig. 4 Comparison of 3D direct simulation and experimental results of porous copper at different porosity

表1 金屬銅的狀態方程參數[26]Table 1 The EOS parameters of Cu samples[26]

表2 金屬銅的SG 本構模型參數[26]Table 2 The SG parameters of Cu samples[26]

回到金屬層裂區再壓實問題當中，來考察圖2 中的幾種不同層裂區初始拉伸狀態對再壓實后物質狀態帶來的影響。

在僅含層裂片（圖2(a)情況下，設置初始孔隙度 α=2 ，初始銅層裂片以- 1.0 km/s 速度向=0 固壁面運動（即再壓實速度=1 km/s ），層裂片數取不同值的模擬結果參見圖5～6。其中，圖5 給出了=8,20下層裂區在再壓實過程中典型時刻的材料內部密度狀態；圖6(a)給出了不同層裂片數量下層裂區平均密度 ρˉ 隨再壓實時間變化曲線，曲線峰值即為層裂區再壓實密度；圖6(b)給出了層裂區再壓實密度隨建模中層裂片數的變化情況。可以看到，僅含層裂片情況下，隨著層裂片數的增加，層裂區再壓實狀態逐漸收斂，收斂情況下的再壓實狀態可作為宏觀模擬的比對參考值。

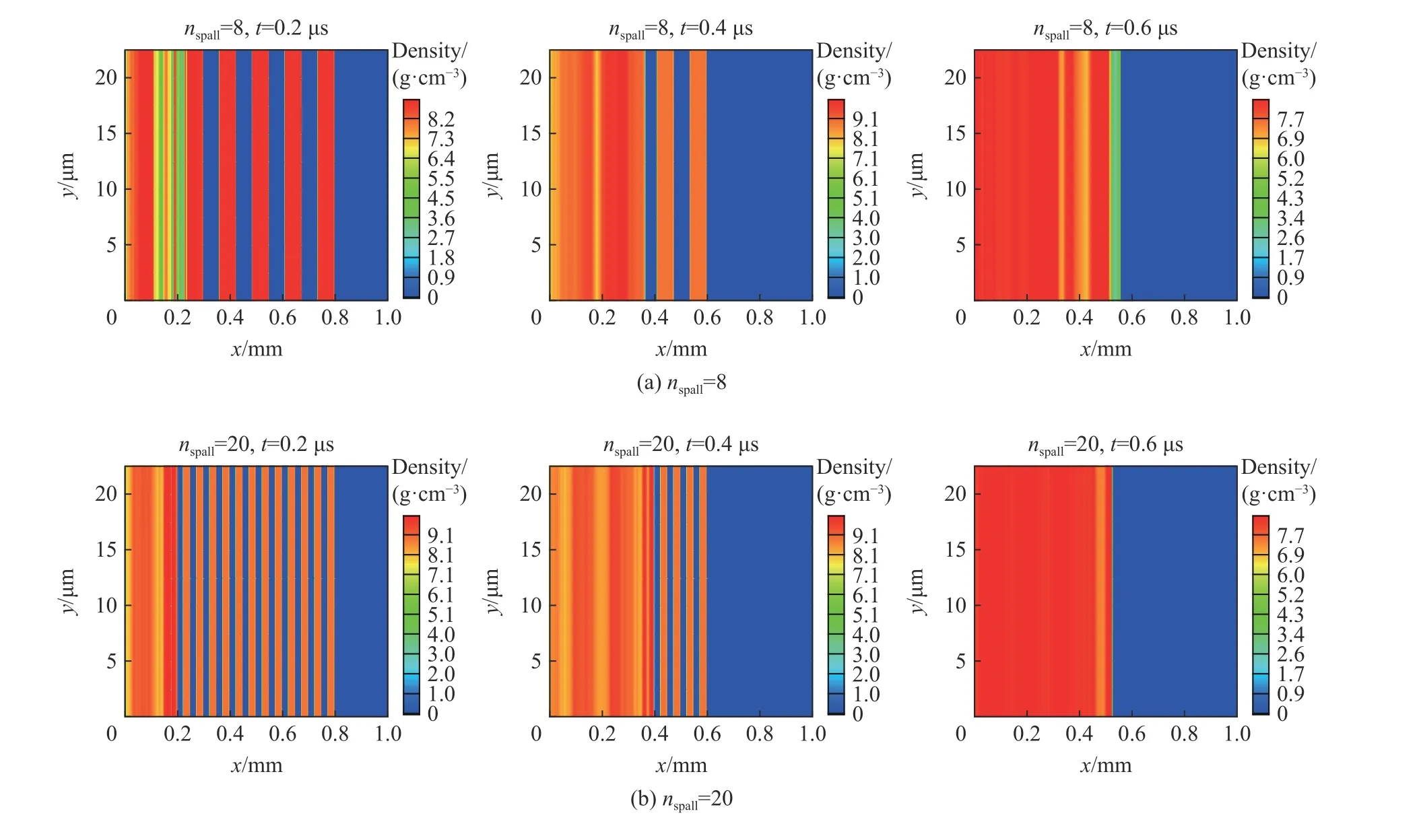
圖5 層裂片數 nspall=8,20 下典型時刻的層裂區壓縮狀態Fig. 5 The compression state of the spallation zone at different times with nspall = 8, 20

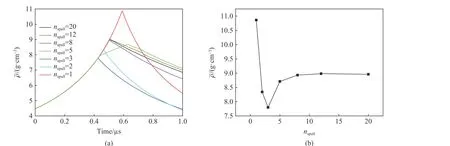
圖6 相同初始孔隙度情況下平均密度的變化Fig. 6 Variation of the average density under the same initial porosity

在僅含孔洞（圖2(b)的情況下，設置初始孔隙度 α=1.3 ，同時在孔洞大小、間距相等假設下設置孔洞數=12。圖7～9 給出了再壓實速度=1,0.5,0.3 km/s 下的三維直接模擬結果，及對應速度下層裂區平均密度隨時間變化情況。受平均密度統計方法等因素影響，孔洞塌縮射流擊穿層裂區外界面后的層裂區平均密度、再壓實密度已沒有實質意義。由于層裂區再壓實后形成了界面向外的高速物質噴射，本文中認為此時的金屬層裂再壓實后已難以作為單一問題研究，應分為孔洞閉合后的基體區和界面噴射區兩個子區域分別進行考慮。

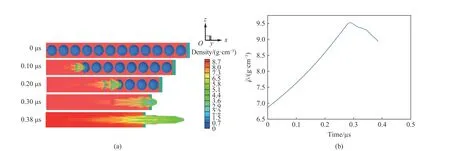
圖7 初始孔隙度1.3、再壓實速率1.0 km/s， nb=12 情況下的密度圖和層裂區平均密度隨時間的變化Fig. 7 Results of the density distribution and average density over time by direct simulations with α0=1.3, v0=1 km/s ,nb=12

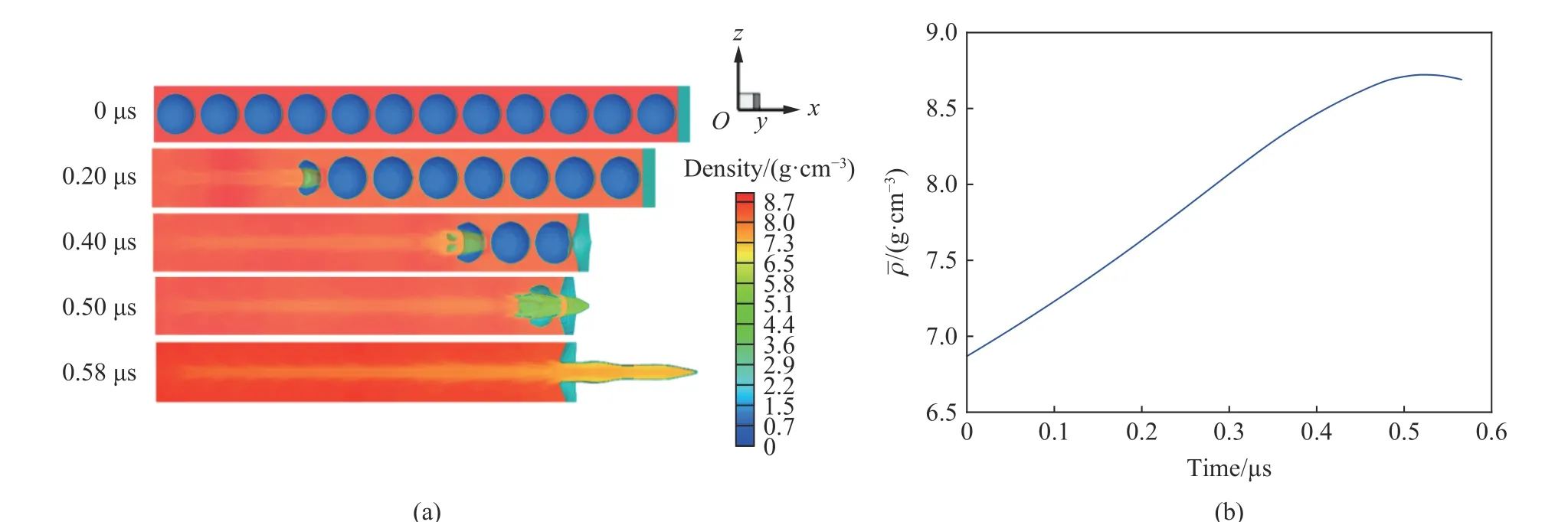
圖8 初始孔隙度1.3、再壓實速率0.5 km/s， nb=12 情況下的密度圖和層裂區平均密度隨時間的變化Fig. 8 Results of the density distribution and average density over time by direct simulations with α0=1.3, v0=0.5 km/s ,nb=12

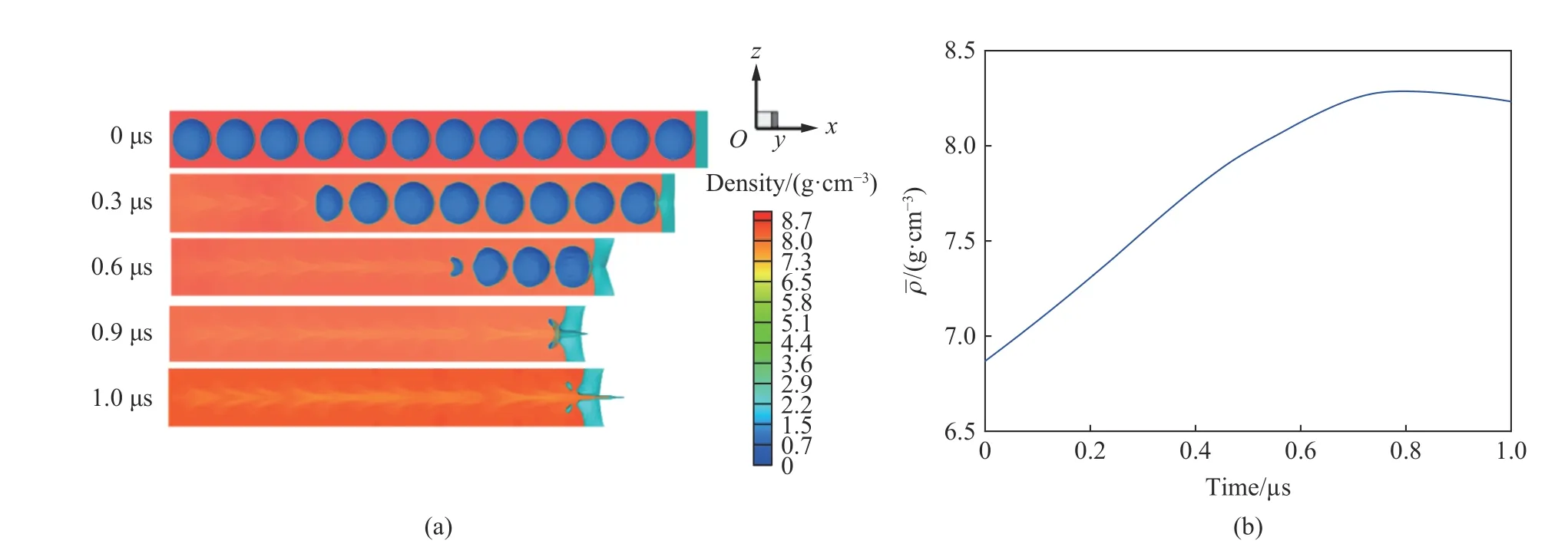
圖9 初始孔隙度1.3、再壓實速率0.3 km/s， nb=12 情況下的密度圖和層裂區平均密度隨時間的變化Fig. 9 Results of the density distribution and average density over time by direct simulations with α0=1.3, v0=0.3 km/s ,nb=12

對于同時含有孔洞、層裂片的層裂區（圖2(c)），保持初始孔隙度 α=1.3不變 ，設置孔洞數=10,層裂片數=10。需要指出的是=10,=10 情況下的建模并不唯一。圖10～12 給出了再壓實速率分別為=1.0,0.5,0.3 km/s 情況下的直接數值模擬典型時刻密度圖，及對應情況下層裂區平均密度隨時間變化情況。可以看到，同時含有孔洞、層裂片的層裂區再壓實后的表面噴射較少、界面速度差異不大，并沒有出現純孔洞情況下那樣嚴重的表面噴射現象。此時統計得到的再壓實密度具有一定的參考比對價值。

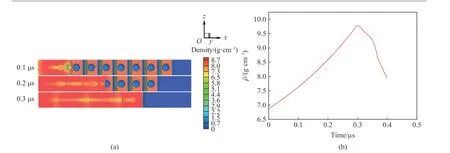
圖10 初始孔隙度1.3、再壓實速率1.0 km/s， nb=10 ， nspall=10 情況下的密度圖和層裂區平均密度隨時間的變化Fig. 10 Results of the density distribution and average density over time by direct simulations with α0=1.3, v0=1 km/s ,nb=10, nspall=10

圖11 初始孔隙度1.3、再壓實速率0.5 km/s， nb=10 ， nspall=10 情況下的密度圖和層裂區平均密度隨時間的變化Fig. 11 Results of the density distribution and average density over time by direct simulations with α0=1.3, v0=0.5 km/s ,nb=10, nspall=10

圖12 初始孔隙度1.3、再壓實速率0.3 km/s， nb=10 ， nspall=10 情況下的密度圖和層裂區平均密度隨時間的變化Fig. 12 Results of the density distribution and average density over time by direct simulations with α0=1.3, v0=0.3 km/s ,nb=10, nspall=10

3 金屬層裂區再壓實過程的宏觀有限元模擬

在層裂區內部層裂片/孔洞的大小、間隙相等假設下，初始時刻所有宏觀網格密度相等，即有初始時刻 ρ=ρ(=1,···,) 。圖13 給出了將層裂區初始均勻剖分為=20 個網格的宏觀計算模型。本節宏觀模擬使用基于四邊形網格的二維有限元方法程序，該程序在宏觀彈塑性流體力學模擬中具有較好的模擬效果。其中，宏觀模擬中使用的邊界條件、材料本構及EOS 均與直接數值模擬相同。

圖13 宏觀上將層裂區初始均勻剖分為nelem=20Fig. 13 Finite element method is used to simulate the spallation zone described by nelem=20

網格斷裂后處理算法是宏觀層裂再壓實問題模擬準確性的基礎，本文處理如下：對于網格斷裂后的應力計算，結合式(2)、(4)可知，在網格斷裂后（＞）應設置網格應力為零；對于網格斷裂后的溫度計算，以最簡單的保持斷裂時刻溫度不變進行處理，將網格斷裂狀態下塑性功、沙漏力等造成的溫升全部置零。

圖14 中給出了宏觀模擬平均密度 ρ（黑色線）與不同初始拉伸狀態下直接模擬得到的平均密度ρˉ（虛線）隨時間變化的對比，其中平均密度曲線峰值及對應時刻即為再壓實密度及再壓實所用的間隔時間。由圖14 的對比看到，宏觀模擬所設置的斷裂后處理算法能夠較好比對層裂區僅含層裂片及同時含有層裂片及孔洞的情況，再壓實密度、再壓實所用的時間間隔及卸載歷程均基本相符。

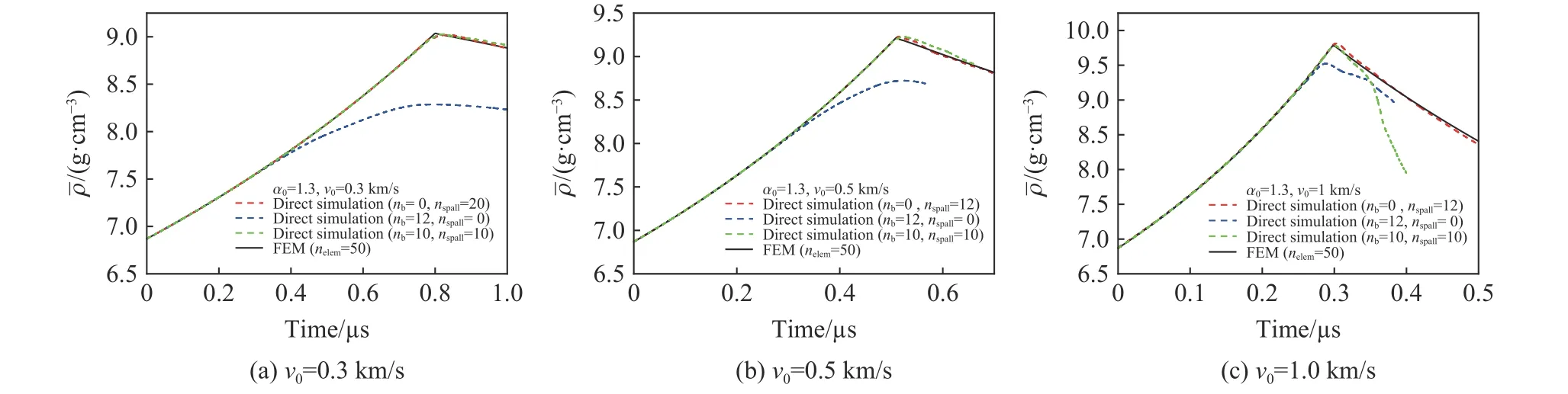
圖14 不同拉伸狀態下的層裂區再壓實平均密度演化的對比Fig. 14 Comparison of the average recompression density under different tensile conditions

為了進一步驗證上述認識，圖15 額外給出了3 組不同孔隙度、不同再壓實速度下的宏觀模擬平均密度與僅含層裂片的直接模擬結果（虛線）對比看到，在較大的孔隙度、較高的再壓實速度下=50 的宏觀模擬結果仍然能較好比對直接模擬得到的再壓實密度及時間間隔。=12的宏觀模擬結果在再壓實狀態上存在一定差異，說明宏觀模擬中層裂區劃分網格數也會對該現象的模擬結果造成一定影響。即宏觀上較好模擬層裂再壓實問題的前提是層裂區的網格數需要超過一定數量，該網格數與宏觀模擬程序相關（經驗證對本文程序而言＞20 即可）。

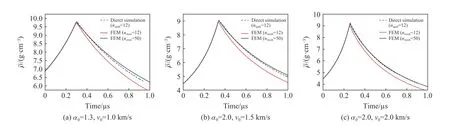
圖15 不同孔隙度、不同再壓實速度下的宏觀模擬與直接模擬的對比Fig. 15 Comparison of the average density obtained from the macro- and direct simulations at different α0 and v0

與圖14 的對比同時看到，宏觀模擬不能較好應對的是拉伸狀態為純孔洞的層裂區再壓實過程。這已在第3 節進行了初步說明：純孔洞再壓實情況下產生的界面噴射行為是導致宏觀模擬無法較好比對的原因。其直接原因是：在孔隙度不大情況下僅含孔洞層裂區可能是連通的（如圖3 所示），層裂區后界面追趕形成的彈塑性波可以通過連續體傳導至層裂區前界面從而造成層裂區前界面提前減速，而宏觀模擬中在斷裂網格再壓實前彈塑性波不會跨過斷裂網格向前傳導。

4 總 結

本文中考慮金屬層裂區初始進入再壓實過程時真實拉伸狀態的復雜性，將金屬層裂區初始拉伸狀態設置為僅含層裂片、僅含孔洞、同時含有孔洞與層裂片3 類情況，對不同孔隙度、再壓實速率、層裂片數及孔洞數下的層裂再壓實過程開展了直接數值模擬研究。在驗證含孔直接建模模擬正確性的基礎上，統計得到了多種工況下的層裂區再壓實密度、再壓實時間間隔等物理量，為對應工況下的宏觀模擬提供比對依據。在直接模擬中還觀察到：拉伸狀態為純孔洞且再壓實速率較高情況下，即使層裂區外界面平整光潔，在再壓實后仍然會產生一定程度的外界面物質噴射現象。

由于宏觀模擬不能區分網格內部拉伸狀態，同時探討了宏觀模擬金屬層裂再壓實過程的可靠性問題。得到了如下初步認識：斷裂后處理算法使用了應力置零和溫度不變情況下，宏觀模擬可以較好模擬含層裂片的層裂區再壓實過程，再壓實密度、時間間隔、卸載路徑均能夠與直接模擬結果較好符合，其較好比對的前提是層裂區所剖分的宏觀網格數超過一定數量；若層裂區內部僅含孔洞，則無論孔洞塌縮是否形成界面噴射宏觀模擬均無法較好反映該層裂再壓實過程。上述認識僅為金屬層裂再壓實問題的宏觀精細化模擬提供支撐，在模擬精度要求不高或再壓實時間歷程較短的情況下對斷裂后處理算法和層裂區網格剖分可不做要求。