侵徹過程中彈引螺紋連接結構振動特性研究*

張冬梅，高世橋

（1. 中北大學機電工程學院，山西 太原 030051；2. 北京理工大學爆炸科學與技術國家重點實驗室，北京 100081）

引信體與彈體之間一般的典型連接是螺紋連接。通常人們會認為在彈體保護下，引信體承受的慣性沖擊會小于彈體承受的過載。然而實踐中卻出現了引信體過載峰值高于彈體過載峰值、過載脈寬低于彈體過載脈寬的現象，即引信經受著比彈體更惡劣的過載環境，其原因主要是沖擊在連接處的傳遞上。因此，正確并深入認識侵徹過程中引信體與彈體螺紋連接界面在侵徹過程中的振動特性十分必要。它是智能引信安全性和可靠性設計的關鍵。

對于螺紋連接結構，自從1929 年den Hartog對渦輪機葉片連接螺栓的應力進行了研究，螺紋承載分布特點開始受到廣泛關注。在螺紋承載分布的解析法中，Sopwith 法、Yamamoto 法兩種解析方法得到了較為廣泛的認可，兩種方法類似，都將螺紋看成懸臂梁，并且以螺紋軸向載荷的分布來反映螺紋承載分布。同時，文獻[4-9]也對螺紋載荷分布進行了研究，文獻[10-13]采用有限元方法對螺紋連接結構進行了詳細地分析，其中文獻[13]還對螺紋連接結構的載荷傳遞進行了研究，但他們并未對螺紋連接結構進行理論分析。這些方法能夠很好地反映出螺紋承載的分布情況，但并未對螺紋連接結構的振動特性進行詳細分析。

因此，本文中將彈體與引信體的螺紋連接結構簡化為螺母體與螺栓體的連接結構，對其在侵徹過程中的振動特性進行研究。針對侵徹彈引螺紋連接結構的特點，建立侵徹過程中彈引螺紋連接結構的彈性模型，并計算出彈引螺紋連接結構的有效剛度及固有頻率。另外，為了驗證模型的正確性，將對彈引螺紋連接結構的拉伸過程和彈引螺紋連接結構侵徹混凝土目標的沖擊過程進行有限元模擬和試驗，還將對侵徹過載信號進行時頻分析，并將計算出彈引結構的各階振動頻率，根據彈引螺紋連接結構的固有頻率判斷出包含于實測過載信號中、由于彈引螺紋連接導致的振動頻率成分信號。

1 螺紋彈性模型

1.1 螺紋體的彈性變形

螺紋體是連接螺栓體和螺母體重要環節，螺栓體和螺母體的相互作用也是通過螺紋體來傳遞的，其結構如圖1 所示。通常情況下，螺紋體的質量相對螺栓體或螺母體都是很小的。因此，在動態作用過程中，螺紋體自身的慣性可以忽略，而只體現剛度的特征，剛度特征可通過靜態分析來求得。

根據文獻[3]，對于如圖1 所示的相互接觸并有力作用的三角形螺紋的內外螺紋牙，除了熟知的由于螺紋牙彎曲產生的撓曲 δ外，還有螺紋牙剪切產生的變形 δ，牙根傾斜產生的變形 δ，牙根剪切產生的變形 δ以及螺紋牙徑向擴展、收縮產生的變形 δ，如圖2 所示。

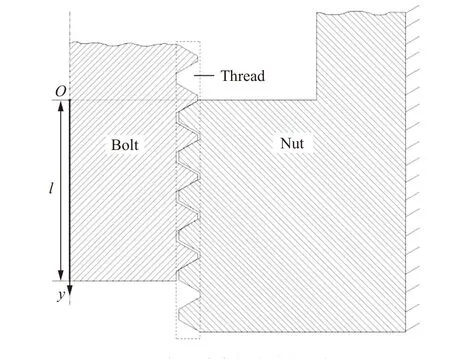
圖1 螺紋旋合部分受力示意圖Fig. 1 Schematic of the force on the screw

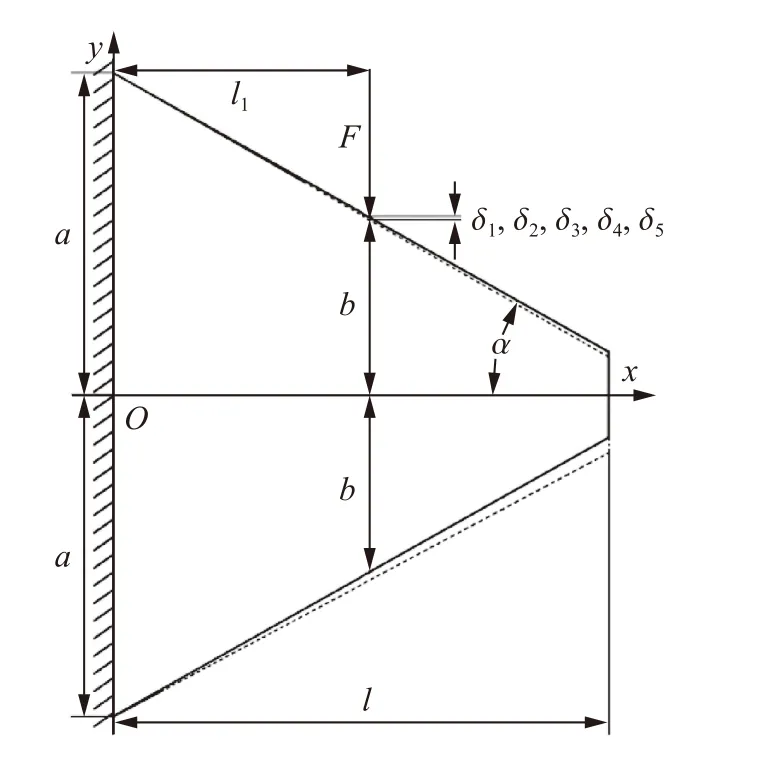
圖2 彎曲引起的變形或剪切引起的變形Fig. 2 Deformation caused by bending or shear

將外螺紋體本體看作是直徑為螺紋有效直徑的實心圓柱，把內螺紋本體看作是外徑為，內徑為的空心圓柱。對于每單位寬度上受單位軸向力作用的螺栓和螺母，螺紋牙的軸向彈性變形分別為：

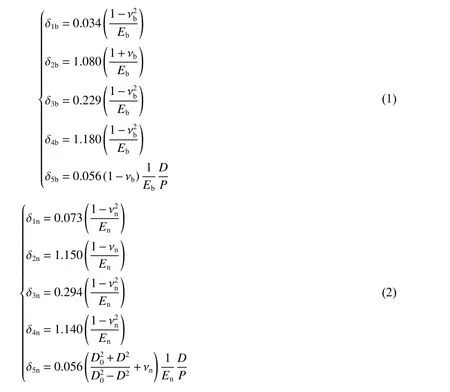
式中：下標中的n 表示外螺紋，b 表示內螺紋；為材料的彈性模量，ν 為泊松比，為螺距。外螺紋和內螺紋的軸向總變形分別為：

1.2 螺紋的變形協調條件

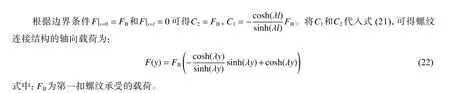
1.3 螺紋等效剛度

2 有限元模擬

2.1 螺紋連接結構拉伸過程模擬

為了研究螺紋軸向載荷分布、螺紋結構的等效剛度以及材料和尺寸參數對螺紋連接結構的影響，建立了一組ISO 標準三角形螺紋連接件的三維有限元模型。螺紋連接結構的有限元模型如圖3所示，為了得到精確的螺紋剛度，模型中只包含了旋合螺紋部分。螺紋拉伸模擬采用ANSYS 軟件進行，由于只考慮螺紋的彈性變形，螺栓和螺母均采用各向同性的彈性材料模型。為了保證計算精度，數值模型全部采用六面體單元SOLID185，接觸單元和目標單元分別采用TARGE170 和CONTA174。在螺栓上表面施加拉力，螺母下表面施加固定約束。

圖3 螺紋結構有限元模型Fig. 3 Finite element model of screw thread structure

數值計算可以得到所有單元的受力，進而可以得出螺紋的應力分布情況并可以計算出每一扣螺紋的承載率。計算還可以得到所有節點的位移，螺栓上表面所有節點位移的平均值 δ 即為螺紋總變形。有限元計算中的螺紋剛度可由下式得到：

為了避免網格密度對結果的影響，計算了不同單元尺寸的拉伸過程，結果發現當螺紋牙截面被分成6 份以上時，計算結果便可滿足精度要求。網格密度繼續增加時，計算精度無明顯改善。

2.2 螺紋連接結構沖擊過程模擬

為了研究螺紋連接結構在沖擊環境下的軸向載荷分布，對彈引螺紋連接結構侵徹混凝土目標的過程進行了有限元模擬，彈引螺紋連接結構及目標的模型如圖4 所示，螺紋預緊力為723 kN。彈引螺紋連接結構侵徹混凝土的模擬過程采用LS-DYNA 軟件進行，有限元模型全部采用六面體單元SOLID164，螺紋連接界面采用面面自動接觸，彈體與混凝土目標采用侵蝕接觸， 彈引系統以324 m/s 的速度垂直侵徹混凝土目標。

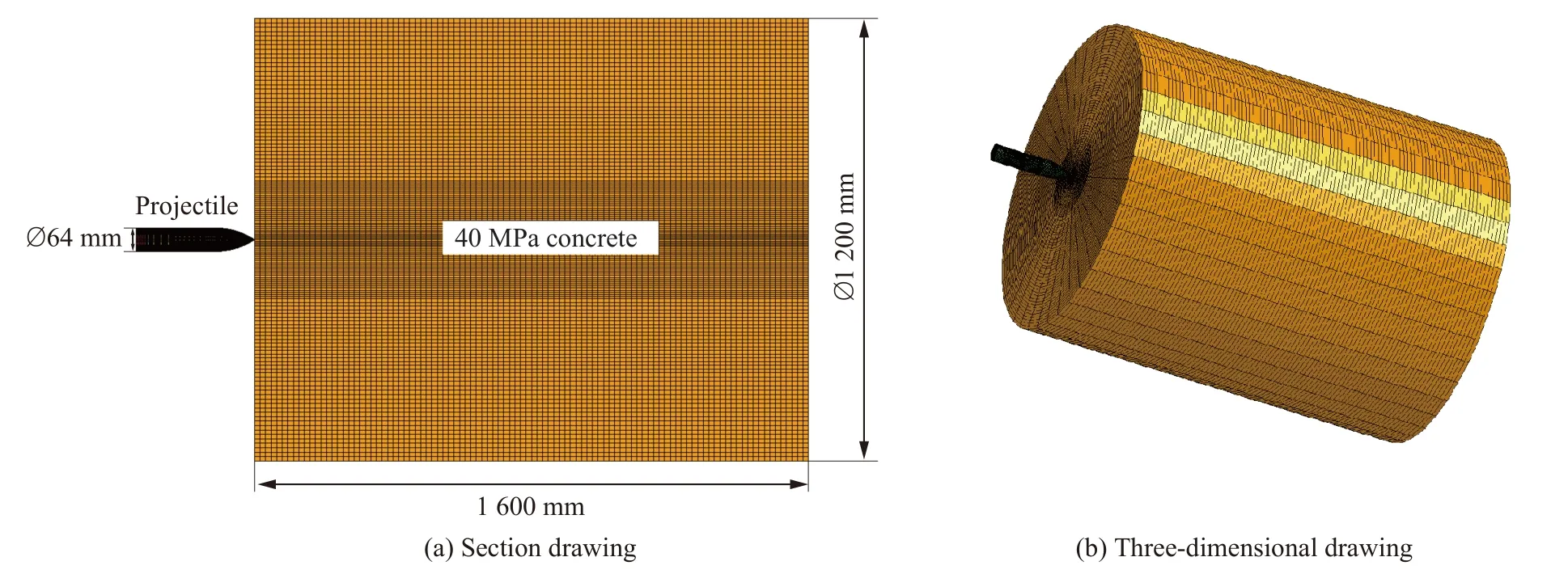
圖4 彈體侵徹混凝土靶的數值模型Fig. 4 The simulation model of a projectile penetrating a concrete target

3 試驗測試

為了驗證螺紋連接結構的剛度，分別對螺紋連接結構進行了拉伸和侵徹混凝土試驗，并將試驗和數值模擬結果與理論計算結果進行了對比。

3.1 螺紋連接結構拉伸試驗

螺紋連接結構拉伸試驗在如圖5 所示的WAW-2000 型液壓式大型萬能試驗機上完成。試驗機夾頭的位移加載速率為1.2 mm/min，拉伸試驗機的力傳感器可以實時測量并輸出拉力值。

如圖5(b)中兩標識線的距離變化量 Δ即為螺紋連接結構在拉伸過程中的變形量，該變化量由非接觸視頻測量系統獲得，視頻的幀率為30 s。試驗中螺紋連接結構的剛度可由下式計算

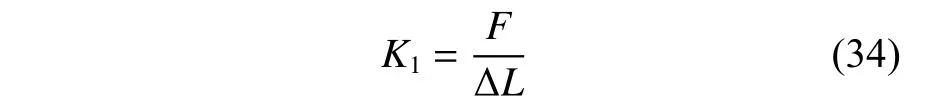
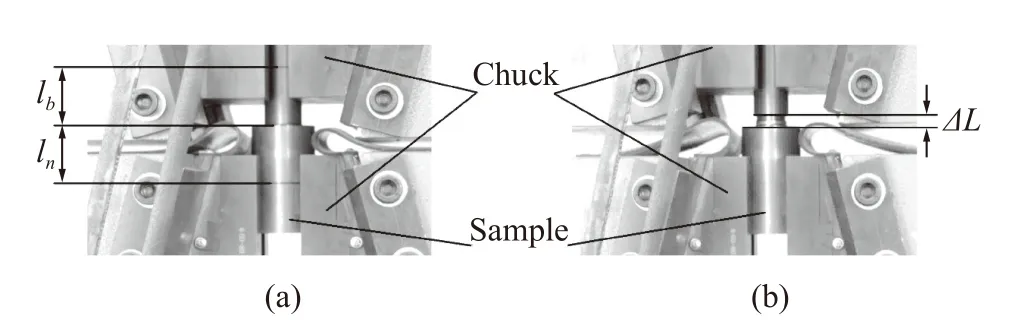
圖5 螺紋拉伸試驗圖Fig. 5 Thread tensile test

式中：為螺紋彈性變形量為 Δ時的軸向力，距離變化量 Δ為螺紋旋合部分的變形。

3.2 彈引螺紋連接結構侵徹混凝土目標試驗

侵徹試驗在口徑為152 mm 的一級輕氣炮上進行，著靶速度為300～400 m/s。使用的高速攝像機型號為FASTCAMSA5，采用的幀率為10 000 s。高速攝像機跟蹤撞擊侵徹過程，獲取彈丸撞擊到靶板上并侵入靶板但未完全埋入靶板的動態過程的直觀圖像資料，通過圖像資料還可以計算出彈體的初始撞擊速度，試驗方案如圖6 所示。

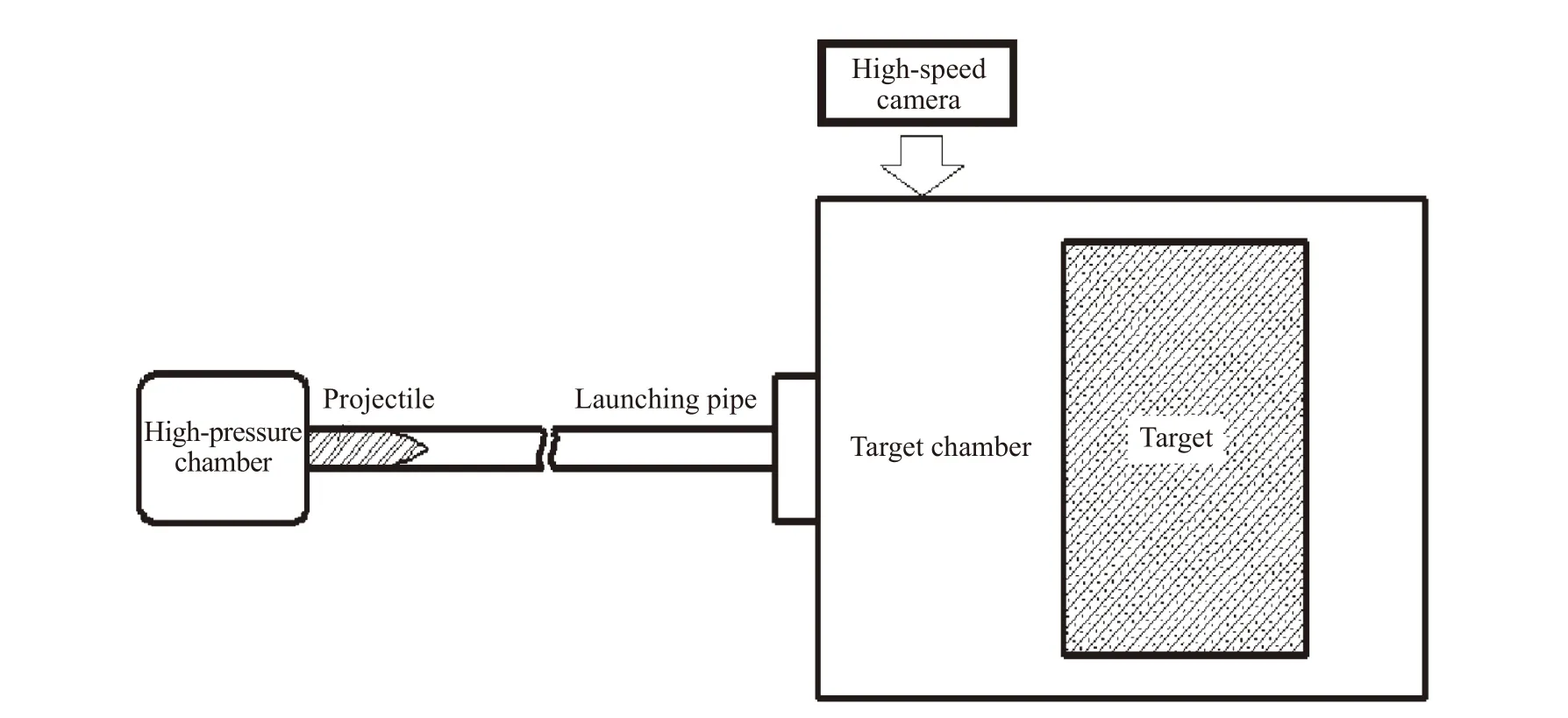
圖6 試驗整體方案Fig. 6 Overall layout of the test

4 過載信號的時頻分析

4.1 彈引系統結構振動頻率分析

侵徹試驗中的彈引系統是一個由彈體、引信殼體、電路板和傳感器等組成的復雜多自由度機械系統，高值加速度傳感器測得的信號既包含了侵徹過程中靶板作用于彈體的剛體過載，也包含了結構的各階振動以及部件間發生碰撞的響應信號。下面通過彈引系統簡化模型對彈體和引信體的振動頻率進行分析。

將彈體和引信體都簡化為一端固定，一端自由的懸臂梁，則彈引系統簡化模型如圖7 所示，在沖擊載荷作用下，懸臂梁會產生軸向振動和橫向振動。根據振動理論的相關原理，彈體和引信體的前六階軸向和橫向振動頻率如表1所示。

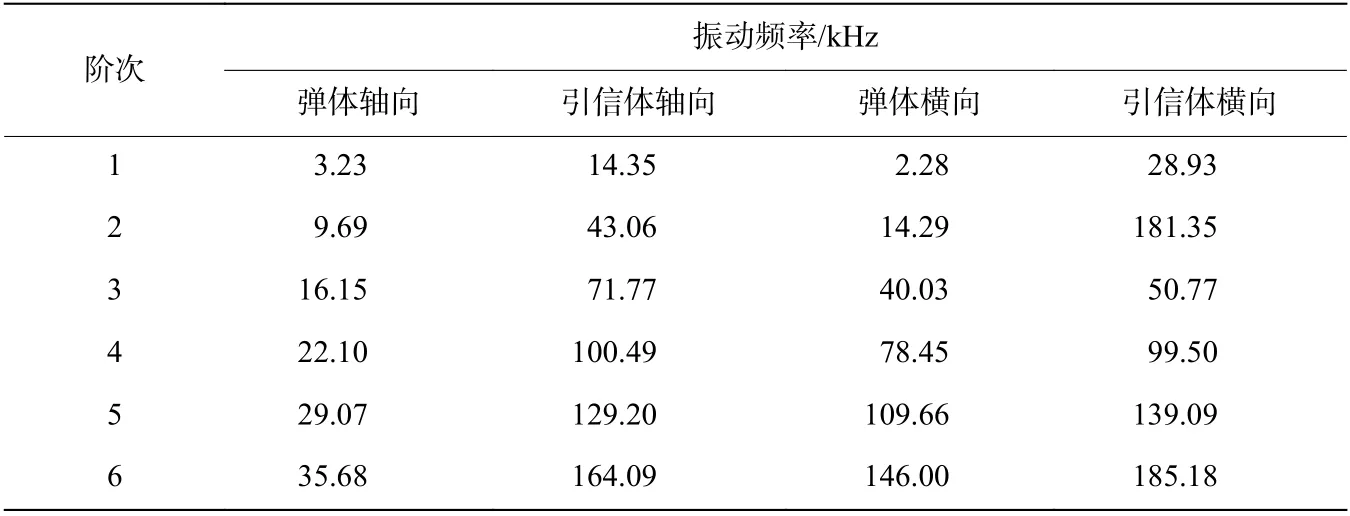
表1 彈體和引信體一～六階振動頻率Table 1 The first to sixth order vibration frequencies of the projectile and fuze

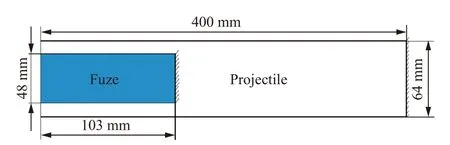
圖7 彈引結構簡化模型示意圖Fig. 7 The simplified model of the projectile-fuze structure

4.2 小波分解

通過對過載信號與小波函數形狀進行匹配，選擇六階Daubechies（db6）小波對實測侵徹加速度信號進行濾波。根據采樣原理，對于侵徹試驗中得到的過載數據，由于其采樣頻率為250 kHz，因此測得的信號成分中最高頻率應該為125 kHz。根據該原理對實測過載信號進行六層小波分解，得到的1～6 層的近似信號和細節信號對應的頻帶如表2 所示，其中，為近似信號，為細節信號，為分解層數。

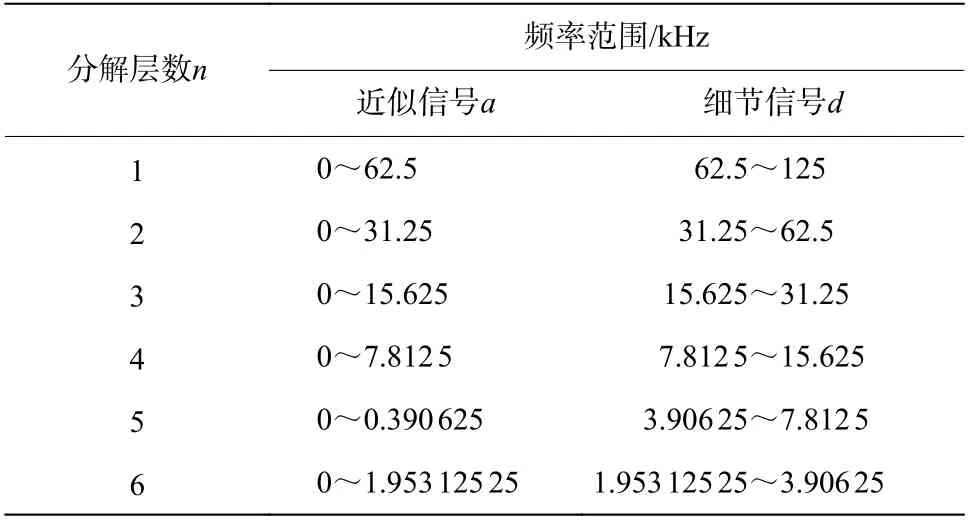
表2 小波分解信號的頻率范圍Table 2 Frequency range of wavelet decomposition signals

侵徹過載測試信號的1～6 層小波分解得到的近似信號及細節信號如圖8(a)所示，其中原始信號可表示成=++++++，近似信號和細節信號的頻率譜如圖8(b)所示。

將圖8(b)中細節信號的主要頻率成分與表3 中的彈體和引信體振動頻率進行對比可知，實測信號頻譜中大部分幅值較大的頻率成分都可以在彈體和引信體的振動頻率中找到對應的值，特別是彈體和引信體的低階軸向振動頻率在實測過載信號的頻譜圖中都有比較明顯的體現。還有一些幅值明顯的頻率成分信號無法在彈引結構振動頻率表中找到，這些頻率成分的高頻信號很有可能是引信體內部器件的振動信號或者是侵徹過程中各部件間產生的碰撞信號。

圖8 過載信號6 層小波分解及其幅頻特性Fig. 8 Six level wavelet decomposition and amplitude frequency characteristics of overload signal

表3 計算結果對照Table 3 Comparison of calculation results

5 結果分析

通過對螺紋連接結構拉伸和沖擊模擬得到的螺紋牙等效應力（von Mises stress）分布如圖9 所示。從圖中可以看出，靠近力作用點的螺紋牙承受載荷較大，遠離作用點的螺紋牙承受載荷逐漸減小，沖擊載荷作用下比靜載荷時減小得更快。第1 扣螺紋承受的載荷最大，沖擊載荷作用下該特性更明顯。

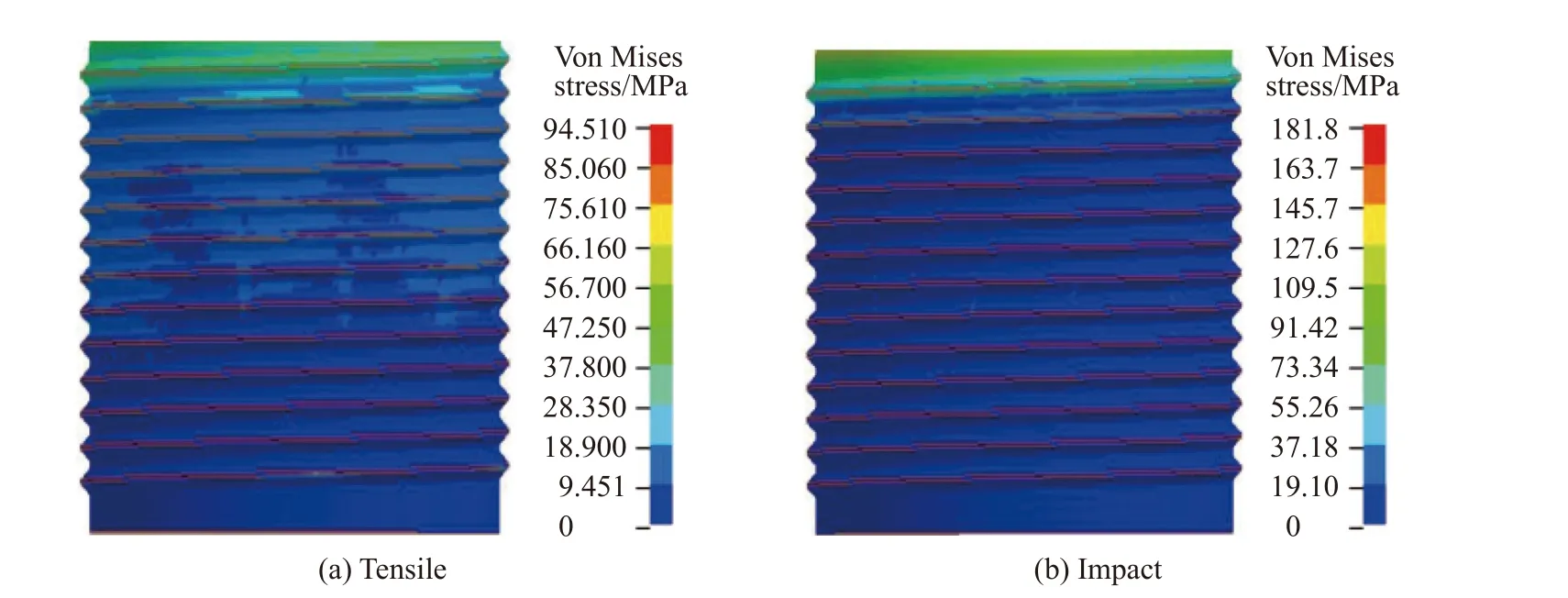
圖9 螺紋牙應力分布Fig. 9 Von Mises stress distribution of screw thread

比較有限元計算、螺紋彈性模型和Yamamoto模型計算所得的每個扣螺紋承載率（每扣螺紋承受載荷與總載荷的比值）如圖10 所示。由圖10 可知，3 種方法得到的螺紋載荷分布趨勢很吻合，但彈性模型和有限元計算結果稍大于Yamamoto 方法的計算結果，特別是第1 扣螺紋牙的承載率差別最大，并且本文中提出的彈性模型計算結果與模擬結果更接近，這主要是因為彈性模型更好地考慮了螺紋上沿螺旋線方向載荷分布不均勻的特性。

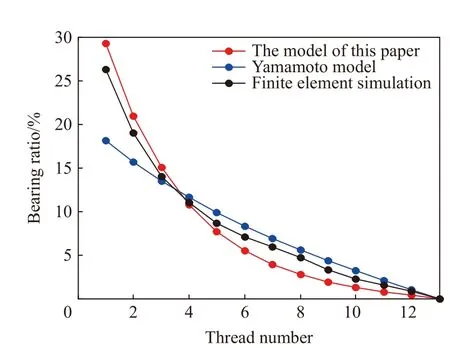
圖10 不同方法計算出的每扣螺紋承載率Fig. 10 Bearing ratio of screw thread calculated by different methods

螺紋連接結構拉伸試驗結果如圖11 所示，從圖11 中可以看出，在軸向拉伸力很小時，螺紋結構變形量較小，螺紋結構處于彈性變形階段；隨著拉伸力繼續增加，螺紋結構開始發生屈服，并進入屈服階段；當拉力超過其強度極限時，螺紋連接結構被拉壞，而曲線初始線性段的斜率就是螺紋結構的剛度。

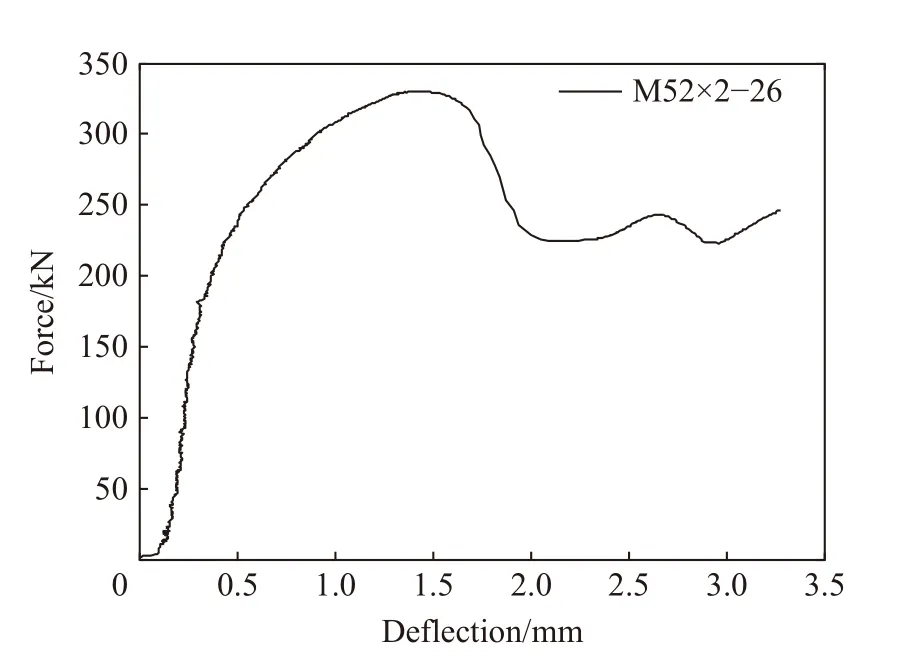
圖11 螺紋連接結構拉力-變形曲線Fig. 11 Tension force-deformation curve of threaded connection structures

將由拉力-變形曲線計算出的螺紋連接結構的強度極限與螺紋材料本身的強度極限對比，如表3 所示。由表3 可知，所有螺紋連接結構的剛度和強度極限都明顯低于螺紋材料本身，這說明螺紋連接結構的剛度明顯小于固連結構。因此，將螺紋連接結構簡單地看作固定連接是不合理的。

表3 還給出了螺紋連接結構的剛度，剛度包括拉伸試驗測量結果、有限元計算結果、Yamamoto 方法以及本文中提出螺紋連接結構彈性模型的計算結果。比較這些結果可知，相對于Yamamoto 方法，彈性模型計算結果與試驗和有限元模擬結果更吻合，這主要是由于通過彈性模型推導出的螺紋連接結構剛度，充分考慮了螺紋沿螺旋線方向載荷分布的不均勻。

另外，對螺紋材料、旋合長度和螺距對螺紋剛度影響進行了分析，結果如圖12 所示。由圖12(a)可知，45 鋼材料螺紋連接結構的剛度最大，紫銅材料的剛度次之，而黃銅材料的剛度最小，即螺紋的剛度隨材料的彈性模量增大而增大。由圖12(b)可知，在螺紋旋合長度較小時，螺紋旋合長度越大，螺紋連接結構的剛度越大；隨著螺紋旋合長度繼續增大，螺紋剛度變化不再明顯。從圖12(c)可以看出，在螺距值較小時，螺紋結構總剛度隨螺距的增大顯著地減小；隨著螺距繼續增加，結構的總剛度變化不再明顯。

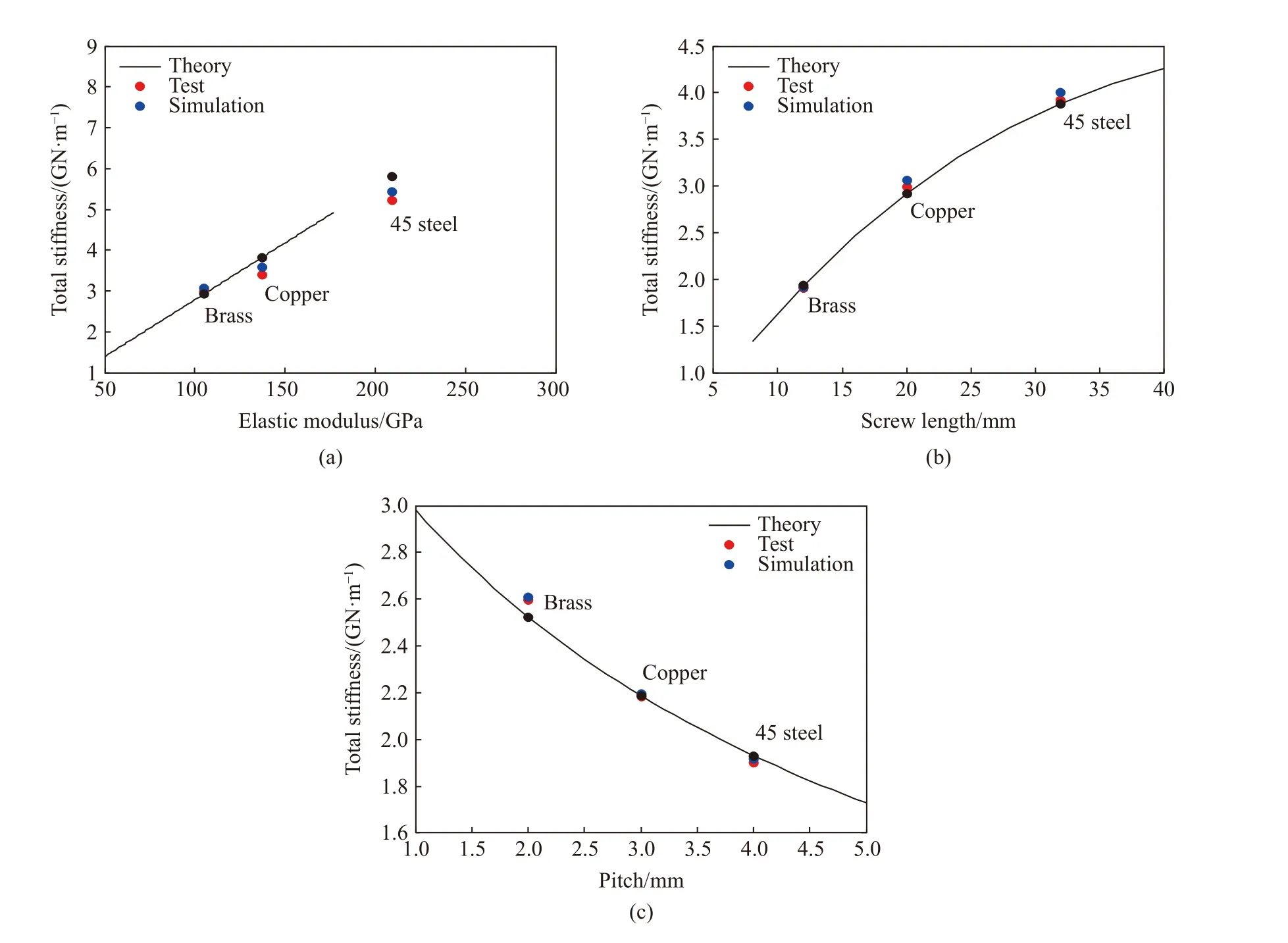
圖12 剛度變化規律Fig. 12 Variation of stiffness

對于著靶速度為324 m/s 的侵徹過程，根據以上螺紋剛度分析的理論模型計算得可以得到彈引螺紋連接結構剛度為5.68 GN/m，拉伸試驗得到的剛度為5.61 GN/m。計算得到的彈引螺紋連接結構的固有頻率為4.5 kHz，由侵徹過載測試數據的小波分析結果可知，這個頻率成分的信號存在于小波分解的第五層細節信號中。通過信號的分析結果發現，在第5 層小波分解細節信號的頻譜圖中，頻率約在4.5 kHz 處存在1 個明顯的峰值，并且該峰值較大，這說明由彈引螺紋連接結構的彈性導致振動信號的幅值較大，這對實測過載信號的影響是很嚴重的。這一結果也說明通過螺紋連接在彈體上的引信體的沖擊環境要比彈體本身的沖擊環境復雜得多。

彈體剛體過載和附加了彈引螺紋連接結構振動響應的過載曲線如圖13 所示。因此，由于螺紋連接結構間沖擊傳遞的彈性特性和碰撞特性，導致通過螺紋連接到彈體上的引信體處于更加惡劣的極端過載環境中。

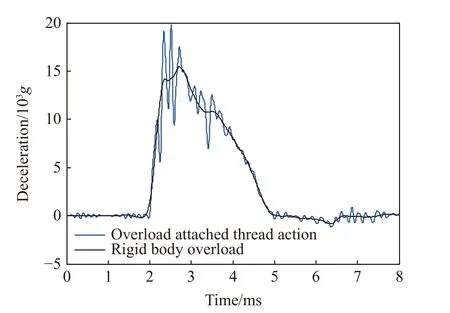
圖13 過載時程曲線Fig. 13 Overload-time curves

6 結 論

本文中針對侵徹過程中的彈引螺紋連接結構，首先，建立了彈引系統螺紋連接結構沖擊傳遞的彈性模型，并通過試驗及有限元模擬方法對模型進行了驗證；然后，進行了彈引系統的振動特性及實測過載信號的時頻特性分析；最后，將計算結果與試驗中測得的過載數據進行了對比，得到了以下結論。

（1）沖擊載荷作用下與靜載荷一樣，螺紋結構中靠近力作用點的第一扣螺紋牙承受的載荷最大，遠離作用點的螺紋牙承受載荷逐漸減小；與靜載荷時相比，沖擊載荷作用下第一扣螺紋承受的載荷更大，遠離作用點的螺紋牙承受載荷減小速度更快。

（2）螺紋連接結構的剛度明顯小于固連結構，因此簡單地將螺紋連接結構視為固連是不合理的。

（3）增加螺紋材料剛度、增加螺紋旋合長度、減小螺距能夠有效增加螺紋連接結構固有頻率。

（4）在侵徹過載測試信號的時頻分析結果中明顯地存在與螺紋連接結構的振動頻率一致的振動信號，并且該頻率成分的信號幅值很高，對過載信號具有很大的影響。