基于溢流前緣長度變化的駝峰堰過流能力擬合

王洪俊

（中山市水利水電勘測設計咨詢有限公司,廣東 中山 528400）

1 前言

巴依托卡依渠首是一座攔河式渠首工程,主要建筑物包括泄洪沖沙閘、引水閘、溢流堰及上、下游河道整治段四部分。溢流堰堰面定型設計為駝峰堰,堰高1.5 m,堰長200 m,溢流堰防沖采用漿砌石斜坡式防沖。本次除險加固設計洪水標準為：P=3.33%,即30年一遇,設計洪峰流量為789 m3/s,閘前設計水位1269.80 m,此時泄洪閘通過流量735 m3/s,溢流堰通過流量54 m3/s。考慮到溢流堰堰頂高程,當水位低于堰頂高程,通過溢流堰的流量為0,水流全部通過泄洪閘下泄。對于開闊的平原地區,駝峰堰堰型選擇不受地形條件限制,在低水頭工況下,該堰型泄流能力較大,且結構簡單,故應用范圍較廣。常用的駝峰堰過流能力計算方法很多,但是大多數計算方法均采用查圖計算的方式,適用范圍相當有限,對于地形陡峭的山區峽谷,駝峰堰堰型設計受到較大限制［1］,無法直接套用現有泄流計算公式。

2 研究方法

為增大溢流前緣長度,以增加其過流能力,并降低堰頂水頭,駝峰堰在平面上大多呈折線形布置。平原河道水庫駝峰堰布置不受地形限制,能通過增大展長,充分利用其低水頭工況下超大的泄流能力；而對于山區峽谷水庫,因受地形限制較大,駝峰堰溢洪道控制數通常較少。

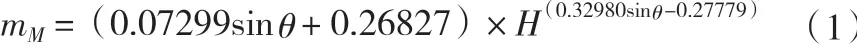
式中：mM為駝峰堰流量系數；H為堰頂水頭,m； 為駝峰堰單峰角度,（°）。

上式中的流量系數取值隨駝峰堰堰頂水頭增大而呈減小趨勢,能較好體現隨水頭增大駝峰堰水流流量持續增加的變動狀態。進而可得出駝峰堰堰頂過流流量,公式如下：

式中：QM為駝峰堰模型堰頂過流流量,m3/s；bM為模型控制段設計寬度,m；HM為模型堰頂水頭,m。

由式（1）所計算得出的駝峰堰流量系數其變動趨勢與工程應用相符,并能體現出隨水頭增大,過堰水流流量隨之增加的趨勢特征,但是其過流能力計算結果和堰頂水頭之間不滿足Q=f（H1.5）的函數關系,且擬合過程中也出現了量綱不吻合現象,其在原型計算中應用時還必須按照幾何比尺L放大處理,即將模型流量系數計算結果與幾何比尺的0.2次方相乘,得到原型流量系數計算結果mp：

在以上分析過程中,均假定以模型控制段過流寬度為駝峰堰過流寬b,且不考慮實際泄流過程中隨堰頂水頭增加溢流前緣長度所發生的變化。

3 駝峰堰過流能力擬合

3.1 過堰水流流態

根據試驗,駝峰堰過堰流態可劃分為完全薄壁堰流、不完全薄壁堰流Ⅰ、不完全薄壁堰流Ⅱ、真空實用堰流等四個階段。在較小流量工況下,水流流經駝峰堰峰頭并貼側堰壁下流時,側堰水流表現為挑射狀；流量增大后,側堰水舌下緣逐漸出現空腔,并逐漸轉移至下游峰頭處,最后連接成帶狀和片狀空腔；流量持續增大后,側堰帶狀和片狀空腔持續轉化為小氣泡移動至下游并最終完全消失。導致駝峰堰流量增大后側堰水舌下緣出現真空的原因主要在于流量達到一定水平后,水流表現為實用堰流,但因駝峰堰水流長度較短,無法對堰水流施加頂托作用。

通過分析駝峰堰水流流態的變化,隨堰頂水深增大,其溢流前緣實際長度L持續減小,其溢流前緣展長優勢逐漸下降至控制段寬度b,其流態也逐漸從薄壁堰流轉向真空實用堰流。通過分析原因發現,隨水頭增大駝峰堰過流能力不斷降低的主要原因在于溢流前緣長度L持續減小。根據對駝峰堰水流流態變動趨勢的分析,可借助薄壁堰流量計算公式（4）以及實用堰成果進行駝峰堰水流流態擬合。

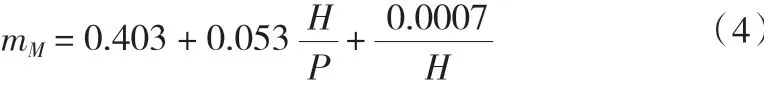
式中：P為駝峰堰堰高,m；其余參數含義同前。

3.2 過流能力

在駝峰堰單峰角度不同,但堰高及試驗條件相同的情況下駝峰堰和實用堰過流能力試驗結果見表1。

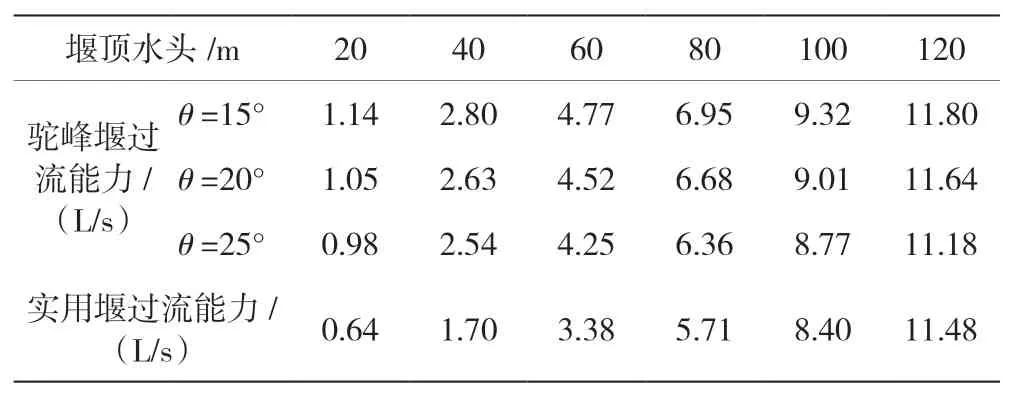
表1 駝峰堰和實用堰過流能力試驗結果

3.3 溢流前緣長度擬合

在流量較小時,駝峰堰溢流前緣長度與實際溢流展長十分接近,而隨流量持續增大,其長度逐漸減小,最終與控制段寬度相等。為此,可認為駝峰堰實際流量系數取值在薄壁堰和實用堰之間,故綜合流量系數M表示如下：

也即,流量系數m和堰流前緣長度L以及堰頂水頭H存在相關關系,可將式（5）變形為：

相關文獻同時將駝峰堰溢流前緣長L表示為單峰角度的函數,具體如下：

式中：c為駝峰堰側堰長,m；a為駝峰堰峰頭長度的1/2,m。

根據現有的駝峰堰過流能力研究成果,將溢流前緣長度值代入堰流基本公式發現,在既定流量和水頭下,流量系數與溢流前緣長度呈反向變動關系。通過薄壁堰流量系數公式及實用堰過流能力相關試驗結果,可得出流量系數取值,具體見表2。表中試驗結果代入駝峰堰堰流基本公式,便可計算出不同駝峰堰單峰角度試驗方案下水頭變化對應的溢流前緣長度值。

表2 流量系數取值

根據水流流態,進行駝峰堰溢流前緣長度與堰頂水頭關系曲線的加密點繪,結果見圖1。

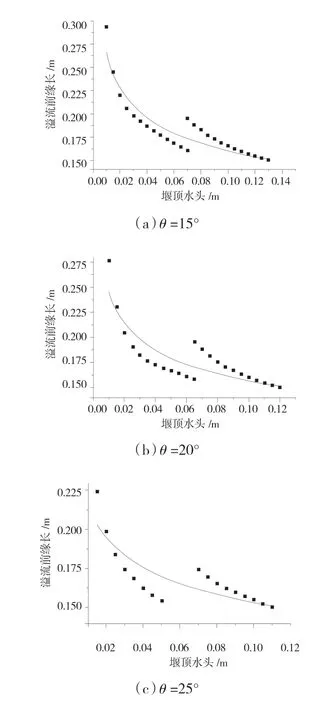
圖1 駝峰堰溢流前緣長度與堰頂水頭關系曲線

根據圖1中所體現的溢流前緣長度與堰頂水頭關系可知,薄壁堰溢流前緣長度與堰頂水頭關系點位位于曲線左側,而實用堰溢流前緣長度與堰頂水頭關系點位則位于曲線右側,兩條曲線存在明顯的分離,且單峰角度越大分離程度越明顯。在曲線偏折處,水頭相同情況下薄壁堰過流能力明顯大于駝峰堰,薄壁堰所計算得堰流前緣長度值偏小；而實用堰過流能力則明顯小于駝峰堰,實用堰所得堰流前緣長度值偏大。駝峰堰過堰水流流態變化是造成這種現象的主要原因,其單峰角度越大,水流過渡至實用堰的堰流也越早。

采用指數函數L=aoHbo進行駝峰堰溢流前緣長度與堰頂水頭關系的回歸分析,所得出的不同單峰角度下駝峰堰擬合結果具體見表3。

表3 駝峰堰溢流前緣長度與堰頂水頭關系擬合結果

根據表3擬合結果,在不同單峰角度下駝峰堰溢流前緣長度與堰頂水頭的相關系數均在0.94以上,且不同單峰角度對應的ao和bo取值存在差異,為此,進一步進行ao、bo及sin 的擬合分析,結果見圖2。

圖2 a0、b0及sin 的擬合分析結果

根據結果可以看出,ao、bo及sin 等參數存在較高的相關性,故可以將ao、bo表示如下：

由此,可以得出駝峰堰溢流前緣長度的表達式,即：

式（10）為隨水頭變化的駝峰堰堰流前緣長度計算公式,據此便可得出不同單峰角度及堰頂水頭條件下溢流前緣長度的擬合結果,具體見表4。

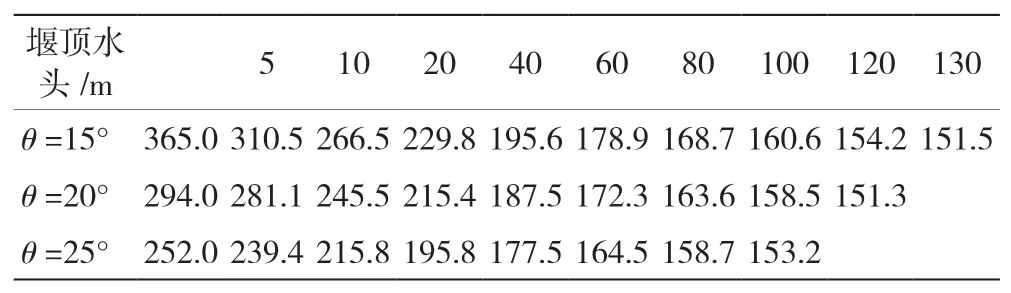
表4 不同單峰角度及堰頂水頭條件下溢流前緣長度的擬合結果

流量較小時所得出的駝峰堰溢流前緣長與實際展長十分接近,而溢流前緣長度隨堰頂水頭的增大而不斷減小,且待流量值達到一定程度后,駝峰堰便轉變為真空實用堰,溢流前緣長及控制段寬取值完全一致,且不再變化。與此同時,在水頭條件相同時,隨著單峰角度的增大,駝峰堰從薄壁堰過渡至實用堰也更為容易［3］。

3.4 流量系數

在式（1）和式（2）的基礎上,用溢流前緣長度形式表示過堰流量,公式如下：

由于流量相等,即Qm=QL,所以：mLL=mMbM,也即：化簡后,流量系數可表示如下：

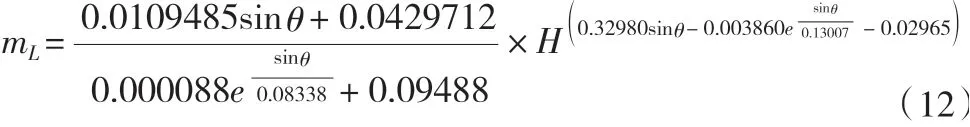
根據式（12）可以得出不同單峰角度下所對應的駝峰堰流量系數取值,具體見表5。

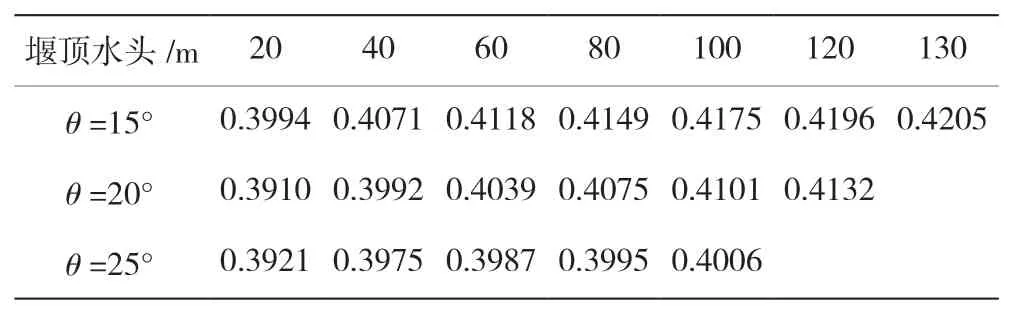
表5 不同單峰角度的駝峰堰流量系數

3.5 流量計算

將式（10）和式（12）代入駝峰堰堰流基本公式后得出如下公式：

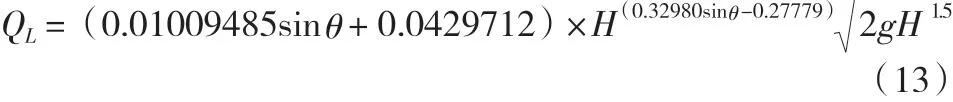
進行駝峰堰過流流量試驗值和擬合公式計算值的比較,具體見表6。

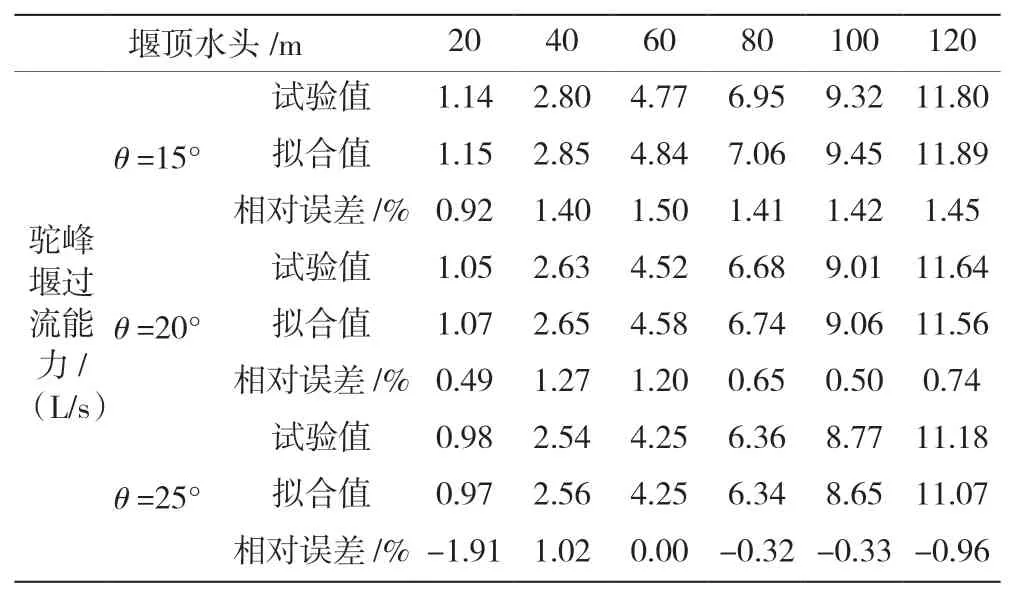
表6 駝峰堰過流流量試驗值和擬合值比較

通過對駝峰堰過流流量試驗值和擬合值的比較可以看出,當駝峰堰單峰角度=15°時,試驗值和擬合值相對誤差最大值為1.45%；當駝峰堰單峰角度=20°時,試驗值和擬合值相對誤差最大值為1.27%；而當駝峰堰單峰角度=25°時,試驗值和擬合值相對誤差最大值為-1.91%,擬合精度符合工程應用。

4 結論

綜上所述,本文依托駝峰堰水工模型試驗成果,并以堰流基本公式為基礎進行流量系數和駝峰堰堰頂水頭的擬合分析,并得出駝峰堰流量擬合公式。基于此得出了可直接用于原型駝峰堰過流能力計算的流量系數公式,且駝峰堰過流流量試驗值和擬合值相對誤差滿足工程應用要求,本文分析結果對水工工程應用具有借鑒指導價值。