基于混合遺傳算法的低碳物流配送路徑優化
胡巧麗,蘭建義(河南理工大學 工商管理學院,河南 焦作 454000)
0 引 言
隨著當前世界經濟環境污染和全球能源供應枯竭的雙重問題日益嚴重,低碳、綠色和環保發展問題日益得到了社會人們的密切關注。在2015年召開的旨在降低碳排放的巴黎會議上,我國政府承諾到2030年單位GDP二氧化碳排放比2005年下降60%~65%。要實現十四五計劃的節約式綠色經濟,重點就要強調綠色低碳經濟的發展,十年內碳排放量達頂峰,2060年前實現碳中和,它揭示了低碳經濟模式是人類社會可持續發展的必然趨勢。近幾年物流服務行業發展快,已成為我國能源消耗及碳排放量大戶。企業要在減少經濟成本的同時,考慮到經濟利益和社會環境的約束,優化物流網絡總體設計結構,實現雙贏互利。
1959年,Dantzig和Ramser首次提出了車輛路線問題(Vehicle Routing Problem,VRP)指滿足某種經濟限制條件下達到一定的目標。關于物流運輸路徑優化的文章不少,例如Roberto等建立VRP模型以減少碳排放,加入汽車速度、坡度等變量,在增加額外運營成本情況下,實現碳減排。Moghaddam等研究了在不確定需求情況下VRP問題,有助于確定可靠計劃及運輸線路,增加客戶滿意度。基于VRP在物流配送領域的廣泛性和應用價值,考慮距離和燃油因素時再重點關注帶時間窗的低碳VRP。硬時間窗雖能準時完成配送,但剛性作用過強,會直接造成低貨車裝載率、長距離高速迂回行駛等不良情況。而軟時間窗有利于柔性配送與運輸成本的降低。本文重點研究帶軟時間窗的VRPTW。例如Qureshi在時間窗懲罰約束基礎上提出軟時間窗約束,由于配送過程的不確定性導致任務在所需時間范圍內不一定完成,如果提前或超過規定時間配送,則直接設置懲罰函數來解決時間因素的相關問題。由于該類問題是典型的NP-hard問題,求解算法有精確和啟發式算法。精確算法適用于規模較小的組合優化問題。啟發式算法可求得問題的次優解或以一定的概率求最優解,其穩定、通用及快速收斂是目前衡量的主要標準,包括節約法、模擬退火法、禁忌搜索法、遺傳算法、蟻群算法等。遺傳算法運算速度雖快,但實現其通用編程語言較復雜,節約法會存在組合點混亂的問題。上述算法單獨使用會早熟且求解質量不高。即本文將全局求解質量高的遺傳算法與局部求解質量高的模擬退火算法結合,對遺傳算法求出的解多次模擬退火尋優,構造一種混合遺傳算法求解帶時間窗的低碳VRP。
1 物流配送路徑優化問題數學模型
1.1 構建帶軟時間窗的車輛路徑問題模型
1.1.1 問題描述
帶時間窗限制的VRP問題相對于基本VRP問題要額外考慮運送時間約束,若未在客戶規定的時間窗內完成配送會產生經濟損失,包括早到閑置等待機會成本和晚到懲罰成本。假設僅有一個配送中心,多輛車向多家配送服務點送貨,每個配送點的地理坐標和平均運貨量一定,每輛車的平均載重量也一定,配送中心在滿足客戶的需求及可接受服務時間的條件下,要求有效實現汽車運行線路的合理安排,使總運輸距離最短,最終車輛服務完每個客戶后返回配送中心。
鑒于實際問題的復雜及不確定性,對帶軟時間窗的VRP做出基本假設:(1)配送中心有且僅有一個,且能滿足所有客戶的貨物裝載;(2)車輛從配送中心出發服務完所有客戶,最終返回配送中心;(3)車輛為同種運輸車型,其運輸總量不能超出其承載容量限制且每位客戶的需求量小于車輛承載容量;(4)每位客戶的位置坐標、需求量和服務時間和接受服務時間都是已知的;(5)到達和離開某個客戶點的車輛都只能是同一輛車;(6)所有車輛必須在規定的時間內返回配送中心;(7)每位客戶必須且只能被訪問一次;(8)城市路網完全通聯,不考慮交通堵塞或交通管制等不可通行情況。
1.1.2 模型中符號和決策變量
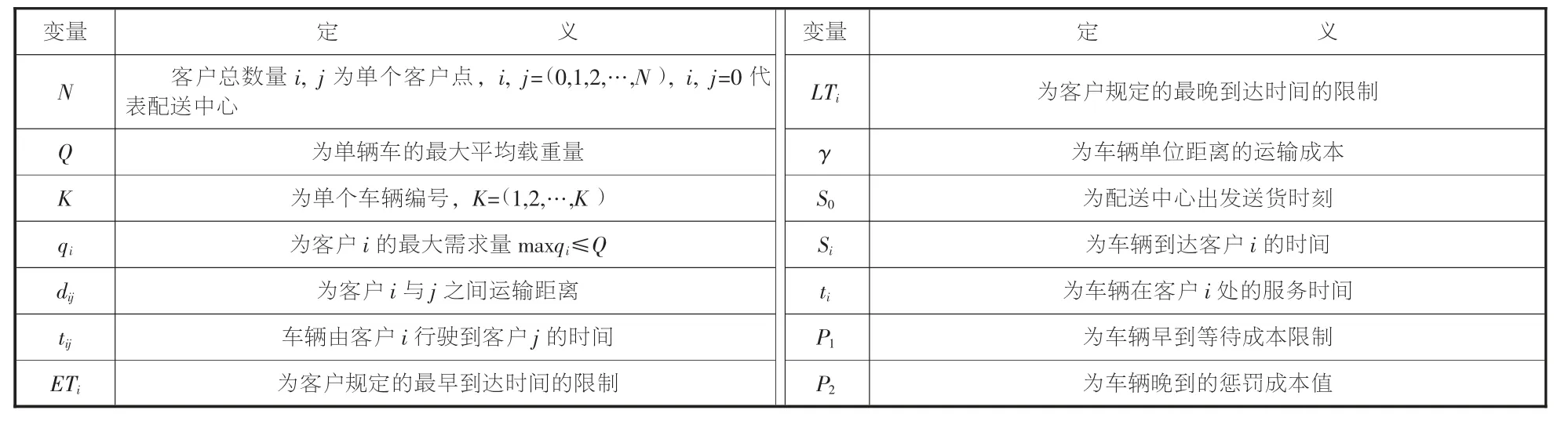
表1 變量定義
1.1.3 模型建立
目標函數:

以總成本最小為目標函數,其中第一項為配送車輛的運輸成本,第二項和第三項為時間窗約束的定量表示。
1.2 構建帶軟時間窗的低碳VRP模型
1.2.1 問題描述
本節研究的軟時間窗的低碳VRP是建立在前一節基礎上,考慮車輛固定用途、燃油消耗、碳排放等費用,求解目標函數總成本。對碳排放量計算,本文考慮了燃油消耗和運輸距離的關系,假設二氧化碳排放與油耗成正比,不考慮行駛速度、路況等因素的影響,得出燃油總的消耗量,再通過燃油轉換系數轉化為該次二氧化碳的排放量,通過對每單位二氧化碳環境成本進行定義,得到最終的二氧化碳的碳排放成本。
1.2.2 模型中符號和決策變量

表2 變量定義
1.2.3 模型建立
(a)目標函數

第一項為車輛配送的固定成本,第二項為車輛配送的運輸費用,第三項和第四項為時間窗的定量表示,第五項為配送車輛的燃油消耗費用,第六項為二氧化碳排放的環境費用。
(b)約束條件
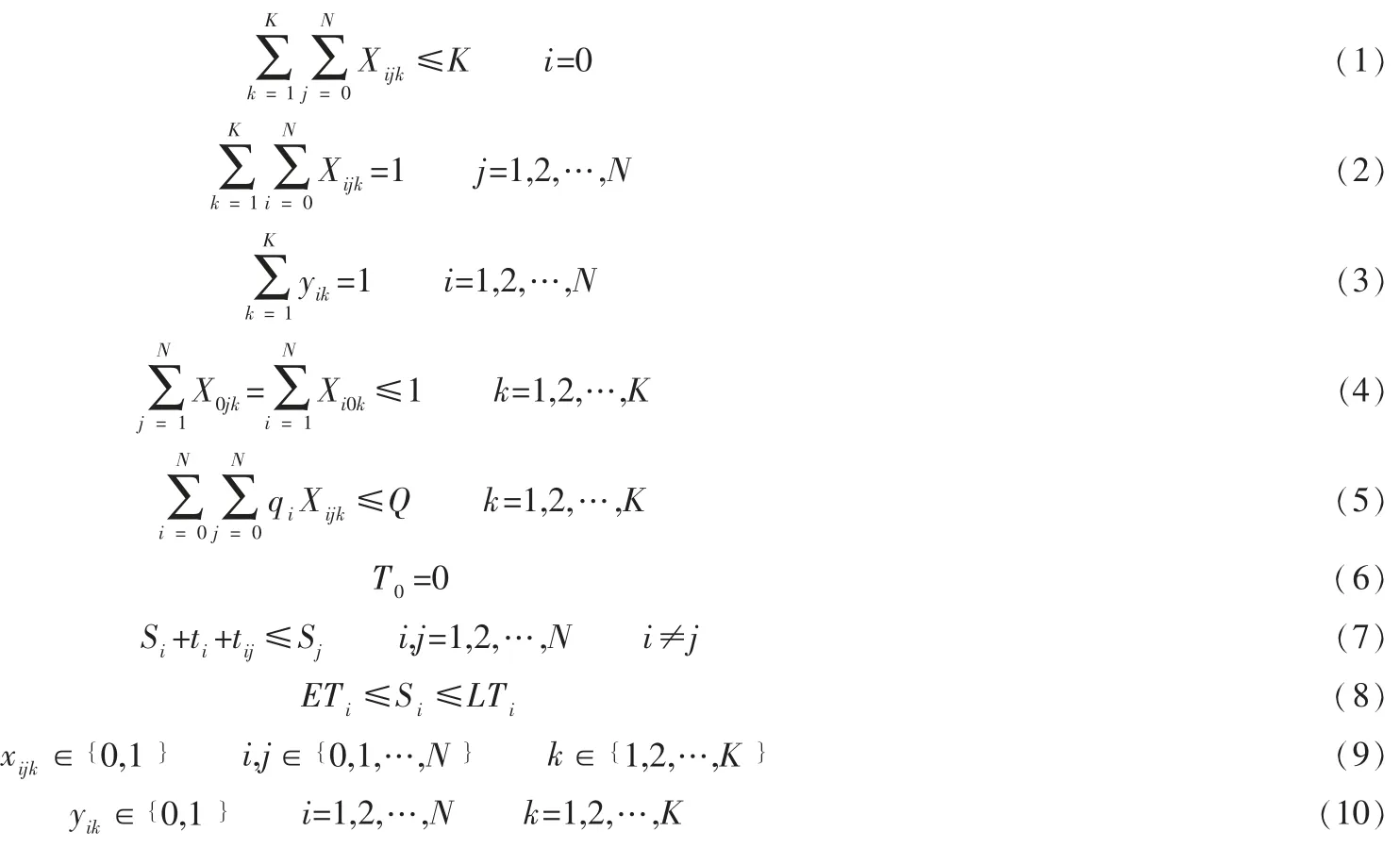
2 帶軟時間窗的低碳VRP的遺傳算法設計
2.1 帶軟時間窗的低碳VRP的遺傳算法分析
2.1.1 算法流程分析
遺傳算法由美國Michigan大學Holland教授基于“優勝劣汰、適者生存”原則對目標函數進行優化,本質是一種高效全局性搜索智能算法,具有強大的魯棒性和全局尋優能力,適合求解多極值和組合性的問題。如圖1為遺傳算法的工作流程圖。
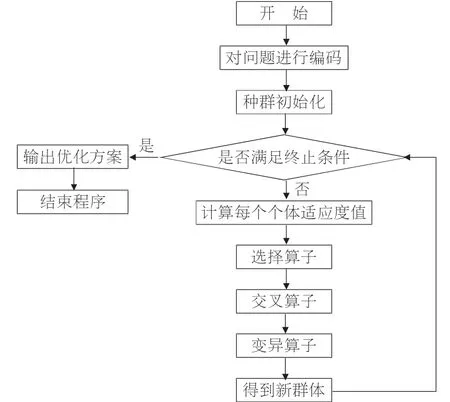
圖1 遺傳算法流程圖
2.1.2 算法實現的具體步驟如下:
(1)改進染色體編碼。采用直接編碼方式,有個客戶,將1~(+ 1)自然數隨機排列,0表示配送中心,將-1個0隨機插入該排列中,由輛車向按1,2,…,編號的客戶送出,最后返回配送中心。根據客戶的需求安排路徑子串,在首尾加0,形成染色體。例如染色體“01402350”表示用2輛運輸車輛從配送中心出發給5個客戶進行配送,共形成兩條路徑的配送。路線1:0→1→4→0;路線2:0→2→3→5→0。
(2)種群初始化。種群生物初始系統是遺傳算法的一個起點,它會對生物進化后的結果產生很大的直接影響。上述隨機程序生成的染色體序列構成一條新的染色體,考慮到實際情況,將初始種群規模設定為100。
(3)計算適應度值。染色體的好壞用適應度值來衡量,適應度值代表最優解的優良程度,在交叉、變異等算子和約束條件下,形成一個個體適應度函數。本文的研究目標是最小配送路徑,可對目標函數取倒數,實現最大值與最小值之間的轉換,目標函數值越小,適應度函數值越大,適應性越強,個體就越優秀,反之個體越差,即:
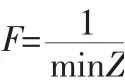
(4)迭代判斷與局部搜索。設置最大進化代數,判斷迭代次數達到預設進化代數時,則停止迭代;否則將迭代次數加1繼續迭代。再選取最優個體進行局部搜索,直至獲得最佳解。
(5)遺傳選擇操作。同時采取最優個體保留戰略和輪盤賭法。將最優個體即適應度最高個體直接復制到下一代。再用輪盤賭,將該種群的所有可用染色體累加得∑F,再計算每條染色體適應度值在體中占比即F/∑F,即為該染色體選中概率。
(6)交叉操作。在遺傳算法中,交叉操作是將兩個隨機的染色體交換某些基因,產生兩個新的基因組合,從而產生兩個新個體。除第一條直接復制的最優染色體以外,其余均以交叉概率為基礎進行配對。由于一個客戶只能由一輛運輸車輛完成配貨,即染色體的編碼中不會產生重復基因代碼。例如:本文對種群中個體交叉采用隨機交叉方式,設有9個配送點,有兩個染色體(0620954078310)和( 0510793082460)。去掉配送中心0變為(629547831)和(517938246),再隨機產生交叉位置,將父代中間部分放在對方前面,如果有重復基因則刪除本身重復數字,從而產生兩個新染色體。例如隨機選擇第二位和第五位為交叉點,則染色體分別為=62|954|7831,=51|793|8246,將染色體中間交配區域加到染色體前面,同理將染色體中間交配區域加到染色體前面:得到=793|629547831,=954|517938246;再分別刪除、交配后與交配區域相同的自然數編碼,得到最終的下一代染色體為:=793625481,=954173826。最終在原有位置重新加載四個0,即最后(=0790362054810,=0950417038260)此法即使是父代相同,也可以產生新的子代。
(7)變異操作。變異操作是指在種群中隨機選擇個體的變異位置,對該基因串的某些個體進行改變,染色體中的一部位發生相應變化,另一部位也會發生相應變化,保證了種群的多樣性與算法收斂性。例如:染色體793625481上的6發生了變異,變為1,則1位上也發生變異,變為6,即得到新染色體793125486。
2.2 帶軟時間窗的低碳VRP的混合遺傳算法分析
模擬退火算法避免了局部最優,可確保全局最佳解的可靠度,通用且適應于并行處理,但運行時間長、收斂速度慢。遺傳算法雖可在更大概率下搜索出最優解,但易早熟、局部搜索能力差、控制變量多。若將模擬退火引入遺傳算法的交叉運作中,使兩種算法結合形成一種混合遺傳算法,使遺傳算法能接收所有解,包括優良解和劣質解,避免在“早熟”解中陷入困境,增強遺傳算法整體收斂性,還可提高進化速度,求得全局最精確解,同時將遺傳算法的迭代次數作為模擬退火算法的退火時間。
2.2.1 算法實現步驟
(1)首先確定種群規模大小,交叉概率P,變異概率P,初始退火溫度,降溫系數θ;
(2)對個體進行編碼,隨機產生個個體,計算個體的適應度值;
(3)對個體進行選擇操作;
(4)分別對個體進行交叉操作和模擬退火工作;
(5)對個體進行變異操作;
(6)降溫,θ,θ為一個[0,1 ]之間的常數,為迭代次數;
(7)判斷個體是否達到進化代數,若達到則終止運算,否則轉回步驟3;
(8)計算結束,得最優解。
2.2.2 混合遺傳算法的構造
(1)編碼。采用1,2,3,…,的自然數編碼。
(2)適應度函數。
適應度代表最優解的優良程度,在函數運算中只有交叉、變異等函數算子和時間等約束條件與目標函數共同作用條件下,才能構造出個體適應度函數。在本文設計的混合遺傳分析算法中可將退火罰因子加入到適應度函數中:
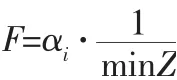
其中:min為目標函數,α為退火罰因素,隨著混合遺傳系統運作,溫度逐漸下降,目標函數值越小,適應度函數值越大,適應性越強,個體越優秀,反之越差,而適應度函數值越大的則有更多機會繁殖新子代,使優秀的混合基因組有更強的遺傳適應性。
(3)選擇算子。采用最佳個體保留方法。
(4)交叉算子。采用類似OX法的交叉方法。
(5)模擬退火算法。
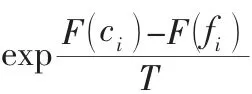
(6)變異算子。為保證個體多樣性,采用連續多次對換變異法。
(7)求取最優解。
3 仿真實驗
3.1 實驗數據
本文假設有21個配送點,中心坐標為(23,5)。對遺傳算法和模擬退火混合遺傳算法均取迭代數為200次,種群大小為100。配送客戶信息如表3所示。
3.2 實驗參數設定
3.3 與模擬退火混合遺傳算法的比較
根據表4所示參數,種群大小為100,迭代次數為200,分別對遺傳算法和模擬退火混合遺傳算法進行仿真實驗對比。將模擬退火算法嵌入原始算法之后,依次用原始方案與新方案對表3數據進行10次求解得兩種方案的對比結果,兩種結果的對比圖如圖2所示。

圖2 兩種算法的對比圖
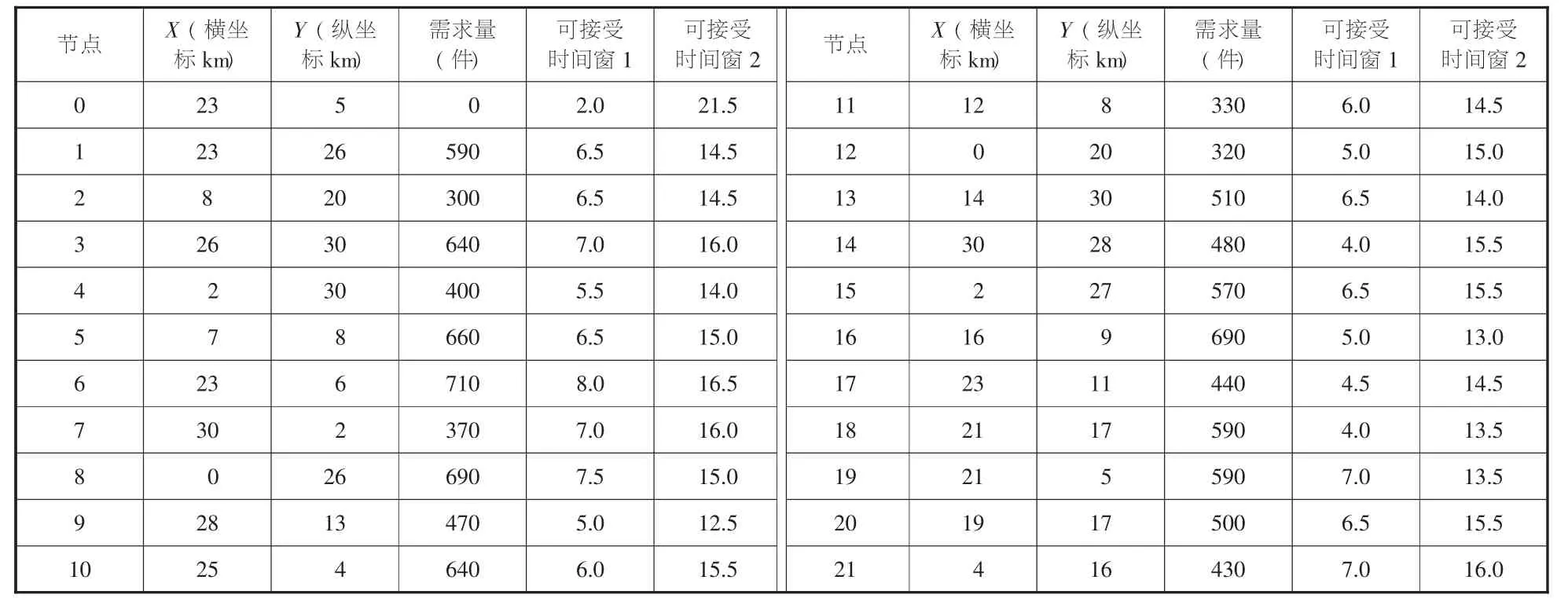
表3 配送客戶信息

表4 實驗參數設置表
遺傳算法所得最優路徑為: [0-7-9-18-5-10-17-15-8-21-19-20-3-14-13-1-2-12-4-11-16-6-0 ],總成本2 095.204元。
加入模擬退火后的混合遺傳算法的最優路徑為: [0-9-14-3-1-18-10-7-17-6-19-20-13-4-15-8-12-11-5-21-2-16-0 ],總成本1 813.970元。
通過圖2可以看出算法迭代過程,遺傳算法要迭代143次左右達到穩定,而加入模擬退火后的混合遺傳算法只需迭代67次左右,說明混合遺傳算法大大提高了收斂速度,最終的路徑優化也比單純使用遺傳算法的成本減少281.234元。圖3、圖4分別為兩種方法所得的路徑示意。
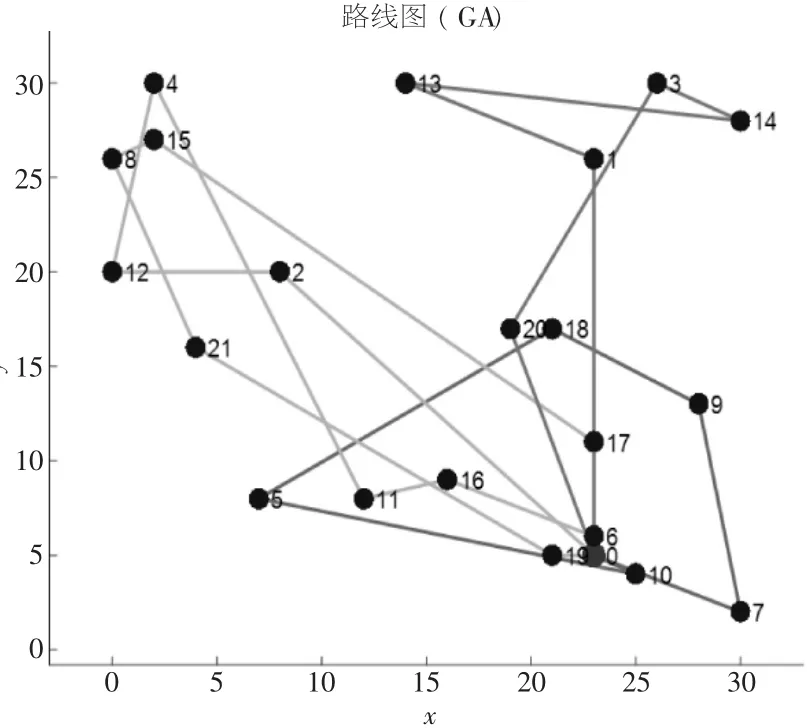
圖3 遺傳算法路線圖

圖4 混合遺傳算法路線圖
運用MatlabR2014b版本編程求解帶軟時間窗的低碳VRP。為了盡可能減少隨機因素的影響,本文對算例重復測試10次,選取測試中得到的最好解和運行結果對比如表5至表8所示。
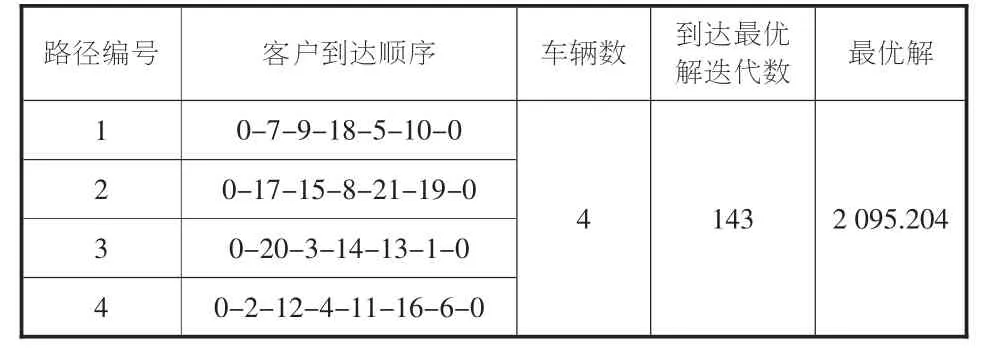
表5 遺傳算法的最優解和具體配送方案

表8 實驗最優解對比
由以上實驗數據對比可以得出,使用混合遺傳模擬退火算法計算的最佳解、最差解、平均解及標準差在兩種算法中都是最小的,達到最優解時的進化代數也是最小的,因此使用混合遺傳模擬退火算法能有效提高對線路優化問解的求解精確度。
4 結 論
本文基于遺傳算法,嵌入模擬退火算法操作,全面提高了遺傳算法性能,增強了遺傳算法在解決配送路徑優化問題時的收斂速度和計算精度,避免陷入最優解的局部,減少了搜索時間,使混合遺傳算法的功效大大提高。實驗結果顯示,該算法是求解帶時間窗低碳物流車輛路徑優化問題的有效方案。

表6 混合遺傳算法的最優解和具體方案方案

表7 各算法10次運行結果比較

