透析本質(zhì) 巧構(gòu)解題
——例談通過解題深化學(xué)生數(shù)學(xué)素養(yǎng)

■ 武漢第三寄宿中學(xué) 陳曼玲

在幾何圖形中設(shè)置動點，探究動點的軌跡，從而研究某些幾何量之間的關(guān)系，這類因動點而產(chǎn)生的最值問題是初中數(shù)學(xué)教學(xué)的熱點和難點。通過對這類問題的分析解決，可以幫助學(xué)生夯實基礎(chǔ)知識和基本方法，培養(yǎng)學(xué)生推理論證等邏輯思維能力，透過表象認(rèn)清數(shù)學(xué)本質(zhì)，巧妙建構(gòu)模型解決問題。

一、典例呈現(xiàn)，提出問題

（2021年武漢市中考16題）如圖（1），在△ABC中，AB＝AC，∠BAC＝90°，邊AB上的點D從頂點A出發(fā)，向頂點B運動，同時，邊BC上的點E從頂點B出發(fā)，向頂點C運動，D，E兩點運動速度的大小相等，設(shè)x＝AD，y＝AE+CD，y關(guān)于x的函數(shù)圖象如圖（2），圖象過點（0，2），則圖象最低點的橫坐標(biāo)是__________.

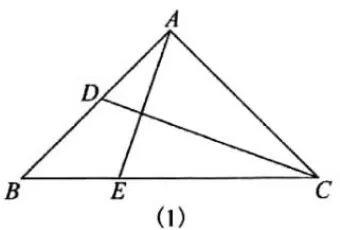
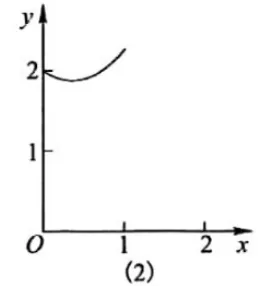
此題從題面上看，將幾何中常見的的三角形圖形與函數(shù)圖象有機的結(jié)合在一起，構(gòu)思新穎，讓學(xué)生覺得似曾相識，一點也不陌生，很愿意去做，但真正做的時候卻有點棘手，是又愛又怕喜憂參半!

二、數(shù)學(xué)建模，轉(zhuǎn)化問題

通過閱讀題目，知道在ΔABC中，D,E兩動點在運動過程中滿足AD=BE，由圖象過點（0，2），可得出AB=AC=1，問題轉(zhuǎn)化為當(dāng)AD為何值時，AE+CD最小，即a+b型最值問題。在這類問題中，我們通常可以轉(zhuǎn)化為“將軍飲馬”或者“三角形中三邊的關(guān)系”來解決，從而找到問題的根本，剩下的就需要借助全等來進行線段的轉(zhuǎn)化了。

三、透析本質(zhì)，巧構(gòu)解題

思路一：如圖1，過點A做AF∥BC（或做∠FAB=450），且AF=AB,連FD,CF，即以AD為邊補了一個角一條邊，則可證ΔFAD?ΔABE（SAS），得FD=AE，于是AE+CD就轉(zhuǎn)化為CD+FD,當(dāng)C,D,F三點共線時CD+DF最小，此時D點運動到G點，即求AG的長，只要解ΔAFG就可以了。在ΔAFG中，已知∠FAB=450，AF=1,可求 ∠AFG=22.50,ΔAFG可解，從而可得。

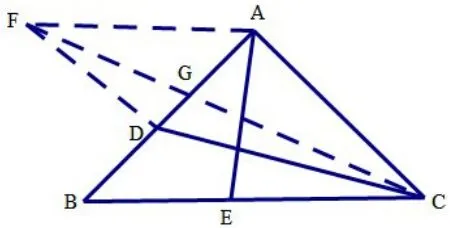
圖1

思路小結(jié)：CD不動，將AE與CD轉(zhuǎn)化到同一個三角形中，從而利用三角形三邊之間的關(guān)系順利找到最值。

思路二：如圖2，過點B作BF⊥BE（或做∠EBF=900），且BF=AC,連EF,AF，即以BE為邊補了一個角一條邊，則可證ΔADC?ΔBEF（SAS），得EF=DC，于是AE+CD就轉(zhuǎn)化為AE+EF,當(dāng)A,E,F三點共線時AE+EF最小，此時E點運動到G點，即求BG的長，只要解ΔBFG就可以了。在ΔBFG中，已知 ∠EBF=900，BF=1,可求 ∠AFB=22.50,ΔBFG可解，從而可得。

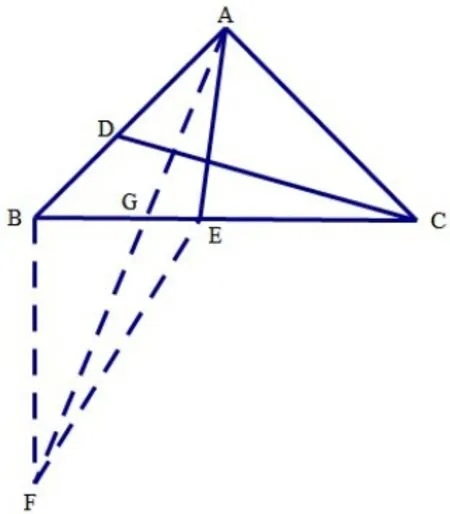
圖2

思路小結(jié)：AE不動，將AE與CD轉(zhuǎn)化到同一個三角形中，從而利用三角形三邊之間的關(guān)系順利找到最值。

思路三：如圖3，過點A做∠DAF=450（或AF⊥BC，或取BC中點均可），且AF=AB，連DF，則可證ΔADF?ΔBEA（SAS），得DF=AE，于是AE+CD就轉(zhuǎn)化為DF+CD,問題轉(zhuǎn)化為在AB上找一點D，使點D到兩定點C,F的距離和最小，即學(xué)生熟悉的“將軍飲馬”問題，我們只需做點C（或點F）以直線AB對稱軸的對稱點H，連FH交AB于點G，則點D運動到點G時，求AG的長即可。做C,H關(guān)于直線AB對稱，可得H,A,C三點共線，AB=AC=HA=AF=1，可證∠H=22.50，解RtΔHAG，可求。

圖3

思路四：如圖4，過點B做∠EBH=900（或BH⊥BC），且BH=AC，連EH，則可證ΔDAC?ΔEBH（SAS），得EH=DC，于是AE+CD就轉(zhuǎn)化為AE+EH,問題轉(zhuǎn)化為在BC上找一點E，使點E到兩定點A,H的距離和最小，即學(xué)生熟悉的“將軍飲馬”問題，我們只需做點H（或點A）以直線BC對稱軸的對稱點F，連FA交BC于點G，則點E運動到點G時，求BG的長即可。做F,H關(guān)于直線BC對稱，可得H,B,F三點共線，AB=AC=HB=BF=1，可證 ∠F=22.50，解RtΔBGF，可求。

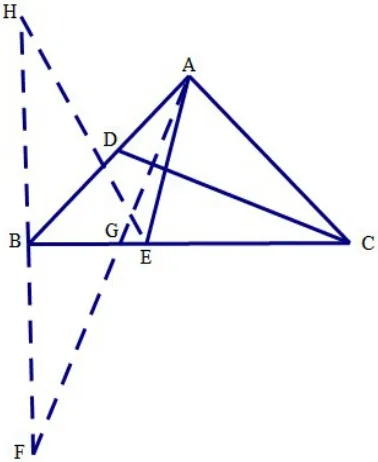
圖4

思路小結(jié)：利用全等，將問題轉(zhuǎn)化為將軍飲馬問題。

對于以上解法，我們在平時教學(xué)中對學(xué)生需多加引導(dǎo)和練習(xí)，找到技巧，學(xué)生自然會理解并熟能生巧，而此題的設(shè)計巧妙之極，不用繁瑣的計算，只需靜下心來思考，頓悟后猶如醍醐灌頂，豁然開朗，問題得到解決，學(xué)生能力顯著提升。

四、深化拓展，提升素養(yǎng)

求a+b型最值方法：等線段全等轉(zhuǎn)化對稱法

1.以相等線段中的一條構(gòu)造等角等邊制造全等；

2.由全等把其中一條動線段a轉(zhuǎn)移到b的另一側(cè)；

3.當(dāng)兩定點在某一直線異側(cè)時利用三角形三邊之間的關(guān)系連接兩定點得到一條線段該線段的長度即為a+b的最小值，當(dāng)兩定點在某一直線同側(cè)時應(yīng)用“將軍飲馬”模型解決a+b的最小值_________。

下面我們通過階梯式的題目設(shè)計來實施模型的應(yīng)用。

例1：AD為等邊ΔABC的高，AB=6,E在AD上，F(xiàn)在AC上，且AE=CF，當(dāng)BF+BE最小時，最小值為__________。

分析：此題比較簡單，等線段條件分明，等線段所在的三角形直觀明了，可直接運用模型構(gòu)造求解。

在圖5中，以AE為邊作∠EAG=600,且AG=BC,則 ΔAEG?ΔCFB(SAS),則EG=BF,求BE+BF的最值轉(zhuǎn)化為BE+EG的最值即可，當(dāng)B,E,G三點共線時，即E點運動到H點時BE+EG=BG最小。在RtΔBAG中，AB=AG=6，則即為BE+BF的最小值。

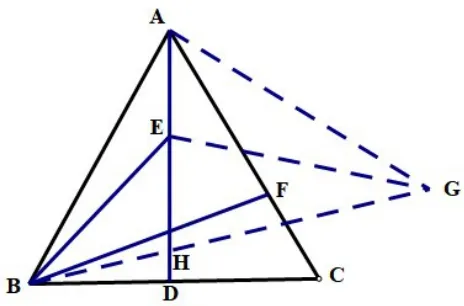
圖5

在圖6中，以CF為邊作∠FCG=300,且CG=AB,則 ΔAEB?ΔCFG(SAS),則FG=BE,求BE+BF的最值轉(zhuǎn)化為FG+BF的最值即可，當(dāng)B,F,G三點共線時，即F點運動到H點時FG+BF=BG最小。在RtΔBCG中，CB=CG=6，則即為BE+BF的最小值。

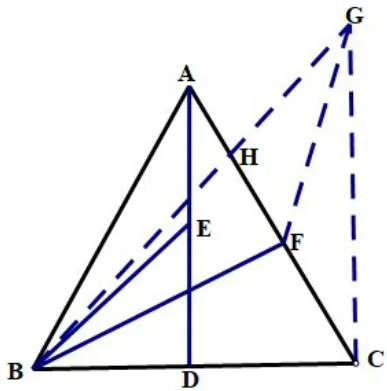
圖6

在圖7中，以AE為邊作∠EAG=600,且AG=BC,則 ΔAEG?ΔCFB(SAS),則EG=BF,求BE+BF的最值轉(zhuǎn)化為BE+EG的最值即可，問題轉(zhuǎn)化為在AD上找一點到兩定點B,G的距離和最小，因為B,C關(guān)于直線AD對稱，連接GC交AD于點H，即E點運動到H點時BE+EG=CG最小。在RtΔCAG中，AC=AG=6，則即為BE+BF的最小值。

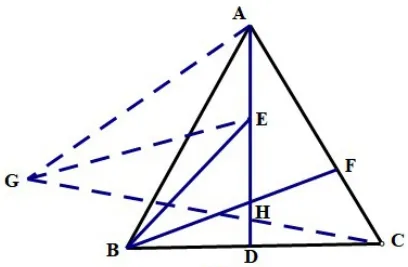
圖7

在圖8中，以CF為邊作∠FCG=300,且CG=AB,則 ΔAEB?ΔCFG(SAS),則FG=BE,求BE+BF的最值轉(zhuǎn)化為FG+BF的最值即可，問題轉(zhuǎn)化為在AC上找一點到兩定點B,G的距離和最小，作B,P關(guān)于直線AC對稱，連接GP交AC于點H，即F點運動到H點時BE+EG=GP最小。可求BE+BF的最小值為。,D是BC的中點，則四邊形DMNC周長最小值為_______。（答案為）

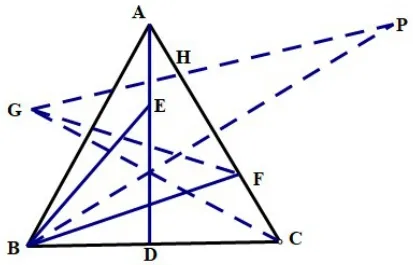
圖8

上述四種方法中，圖8所采取的方法在計算GP時較為復(fù)雜，建議采用另外三種方法。

本題還可以求CE+BF的最小值，方法不變。

例2：如圖9,ΔABC中AC=BC=4,∠ACB=900,線段MN在邊AB上運動，

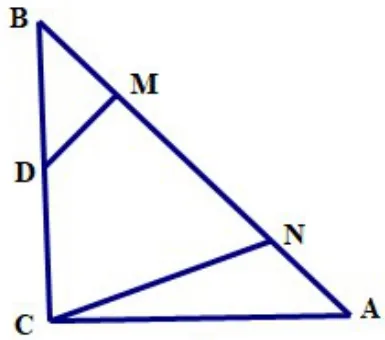
圖9

分析：我們不難發(fā)現(xiàn)要運用上述模型，就需要找到等線段，可過點C作CE⊥AB（或取AB中點，或作∠ACB的角平分線）,得到，于是BM=EN，就可以運用模型構(gòu)造了，下面畫出四種構(gòu)造的圖形，分別見圖10，圖11，圖12，圖13，就不一一贅述了。

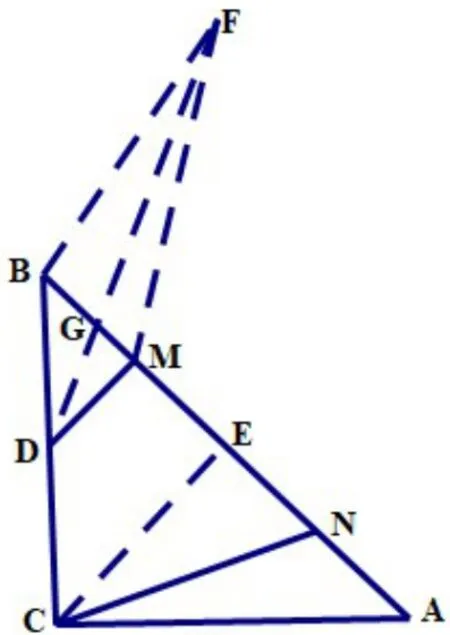
圖10

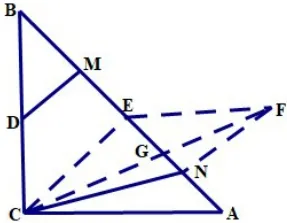
圖11

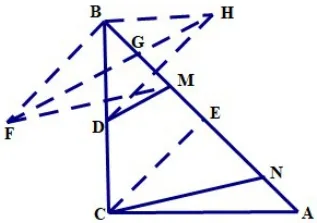
圖12

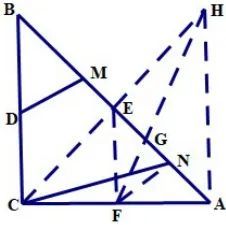
圖13

五、總結(jié)反思，優(yōu)化教學(xué)

1.基本知識點是解決幾何問題的理論依據(jù)

書本上的基本知識點很多，根據(jù)問題有效的正確的運用相對應(yīng)的基本知識，需要我們在平時的教學(xué)中不斷的引導(dǎo)學(xué)生一方面熟悉基本知識，另一方面要在實際的練習(xí)中多加運用，舉一反三，從而提高學(xué)生的數(shù)學(xué)素養(yǎng)。

2.找準(zhǔn)關(guān)鍵條件是解決幾何問題的突破口

題目中的顯性條件運用很重要，但隱含條件推出的結(jié)論，才是突破幾何題目的關(guān)鍵點，一道幾何題的方法往往并不唯一，要善于捕捉題中的信息，找準(zhǔn)關(guān)鍵便可做到一題多解，甚至多題一法。教師在日常的教學(xué)中要有目的地引領(lǐng)學(xué)生逐步學(xué)會，提高學(xué)生的能力。

3.進行常規(guī)思維訓(xùn)練是解決幾何問題的基本

在上述問題中，注重常規(guī)思維訓(xùn)練，注重基本圖形，常見輔助線的添加等常規(guī)經(jīng)驗積累尤為重要。課堂上，教師要讓學(xué)生自己進行充分的探索，可能學(xué)生解決不了問題的全部，但當(dāng)面對一道題時，常規(guī)的思維需要會很快達到，日復(fù)一日的堅持，相信學(xué)生能有效提高數(shù)學(xué)思維品質(zhì)。

4.注重知識的生成過程是解決幾何問題的核心

學(xué)生自己能做的，應(yīng)當(dāng)讓學(xué)生自己去想，把教學(xué)重心轉(zhuǎn)移到引導(dǎo)學(xué)生探索知識的產(chǎn)生，發(fā)展和形成上來，學(xué)生的發(fā)展實際上就是思維的發(fā)展，要提高學(xué)生解決問題的能力，教師就必須讓學(xué)生經(jīng)歷問題解決的全部思維過程，才能使學(xué)生數(shù)學(xué)知識的掌握不僅僅知其然，而且知其所以然，因此，教師轉(zhuǎn)變思想，給學(xué)生自由思考的空間，梳理知識系統(tǒng)，這才是符合學(xué)生長遠(yuǎn)發(fā)展的真正高效率的教學(xué)措施。

總之，初中數(shù)學(xué)可運用的模型很多，教師在平時的教學(xué)中要引領(lǐng)學(xué)生知曉方法，辨明變化，由知一理到通一片，積累解題經(jīng)驗，提升數(shù)學(xué)素養(yǎng)。