從兩個視角探究圓錐曲線中的定值問題
?甘肅省天水市第一中學 方春麗
1 引言
在圓錐曲線問題中,常常出現定點定值問題.求解的思路主要有兩個:一是利用代數的解法求解,即先選擇恰當的基本量,表示出所有的信息,利用代數運算求得結論,再對計算結果進行幾何化的解釋;二是直接利用圓錐曲線的幾何性質進行求解.兩種方法并不獨立,有時也需要配合使用進行證明.在2022屆汕頭市的質量檢測中,考查了一道以橢圓為背景的定值問題,筆者分別從代數與幾何的視角進行了證明,并將該結論推廣至雙曲線與拋物線.現將探究過程展示如下,以饗讀者.
2 題目及分析
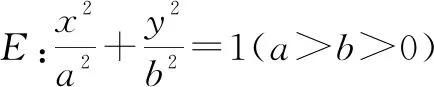
(1)求橢圓E的方程;
(2)若動直線l與橢圓E有且只有一個公共點,過點M(1,0)作直線l的垂線,垂足為Q,試探究:|OQ|是否為定值,如果是,則求出該值;如果不是,則說明理由.
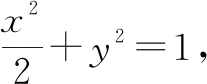
3 解法呈現
解法1:基本量法.
設直線l的方程為x=my+t,與橢圓E聯立,可得(m2+2)y2+2mty+t2-2=0.因為直線l與橢圓E有且只有一個公共點,所以上式的判別式等于零.
化簡可得:t2=m2+2.
①
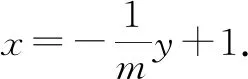
②
將式②代入直線l的方程,可得
③
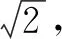
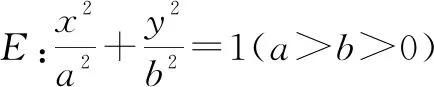
將上述解法一般化即可證明上述結論成立.接下來,筆者將通過幾何的視角來證明.
解法2:利用極點極線,應用幾何法求解.
在證明結論之前,先介紹以下兩個引理.
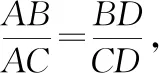
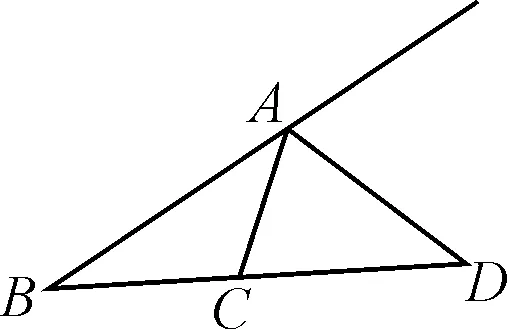
圖1
證明:如圖2,不妨設AB>AC(若AB=AC,則對應的點D不存在),在線段AB上找一點E,使得AE=AC,則∠3=∠4.
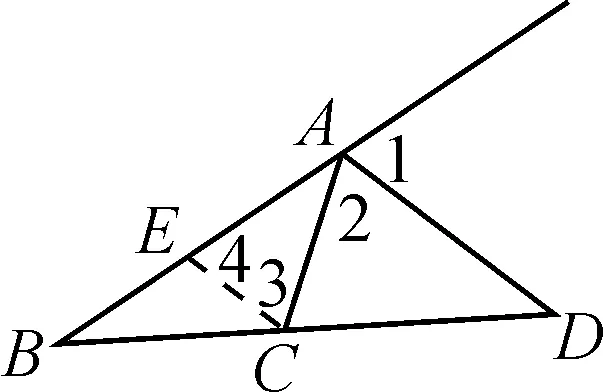
圖2
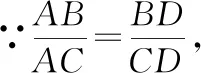
又∠B=∠B,
∴△BCE∽△BDA.
∴CE∥AD,
∴∠3=∠2,∠4=∠1.
因此∠1=∠2,即AD為△ABC對應的外角平分線.
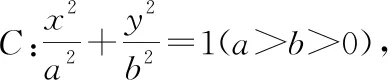
該引理即是橢圓的光學性質:若從橢圓的一個焦點發射出一束光線,經過橢圓反射后會經過橢圓的另一個焦點.
證明:如圖3,設點P的坐標為(x0,y0).根據極點極線[2]的定義可得,過點P的切線l方程為
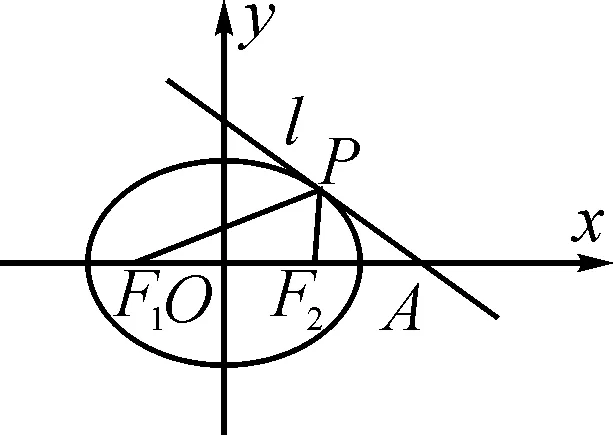
圖3
當直線l與x軸無交點時,結論顯然成立.
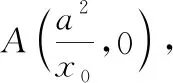
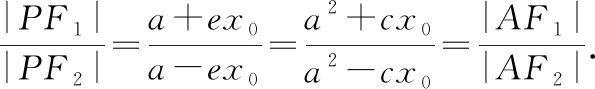
根據外角平分線定理,則可得橢圓過點P的切線為∠F1PF2的外角平分線.
現根據引理證明上述一般性結論.
證明:如圖4,設切線l對應的切點為點A,橢圓E的左焦點為F1,連接MA.過M作切線l的垂線,垂足為Q.延長MQ并與F1A的延長線交于點M′.根據引理2可知,切線l是∠MAM′的角平分線.
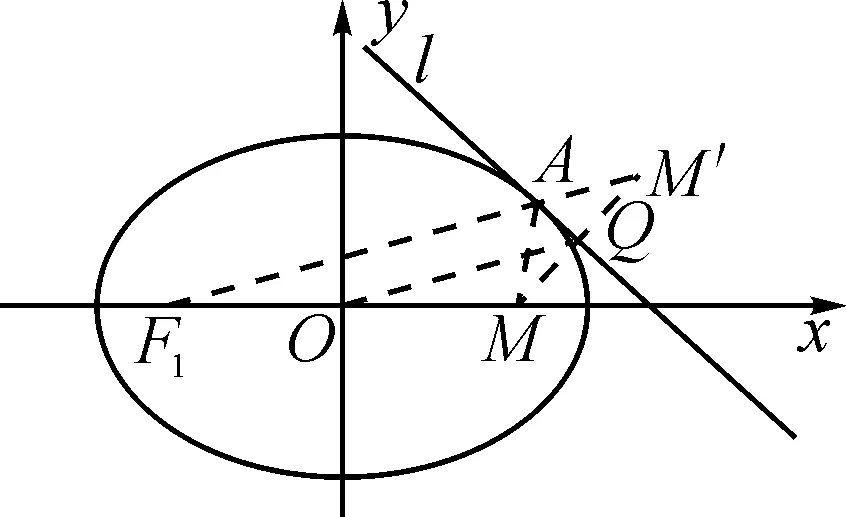
圖4
考慮△MAM′,結合MM′⊥l可得△MAM′為等腰三角形,從而可得AM=AM′,且點Q為MM′的中點.
結合橢圓的定義可得|F1M′|=|F1A|+|AM′|=|F1A|+|MA|=2a.
在△F1MM′中,點O為F1M的中點,根據中位線的性質可得|OQ|=a成立.
根據引理2,切線l為∠MAM′的角平分線,且MM′⊥l,從而可得△MAM′為等腰三角形,且點Q為MM′的中點.
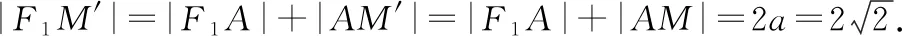
4 命題的拓展與練習
該問題的背景是橢圓,若將橢圓換成拋物線或雙曲線,也有類似結論成立.
定理1:已知拋物線E:y2=2px(p>0)的焦點為M,若動直線l是拋物線E的切線,過點M作直線l的垂線,垂足為Q,則點Q的軌跡為y軸.
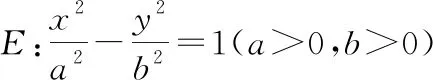
在橢圓以及雙曲線中,所得的點Q的軌跡均為一個圓,所以所求的|OQ|的值為定值.在拋物線中,點Q的軌跡為直線,也可理解為半徑無限大的圓.從這個意義來講,三個圓錐曲線的意義相同.上述兩個定理的證明過程可模仿橢圓中的證明方法即可,但需要了解雙曲線與拋物線的光學性質.現簡介如下:
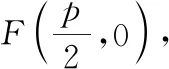

圖5
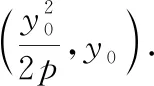
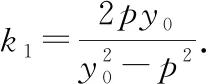
因此α=β.可知拋物線過點P的切線為∠FPP′的角平分線.
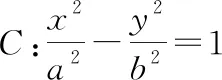
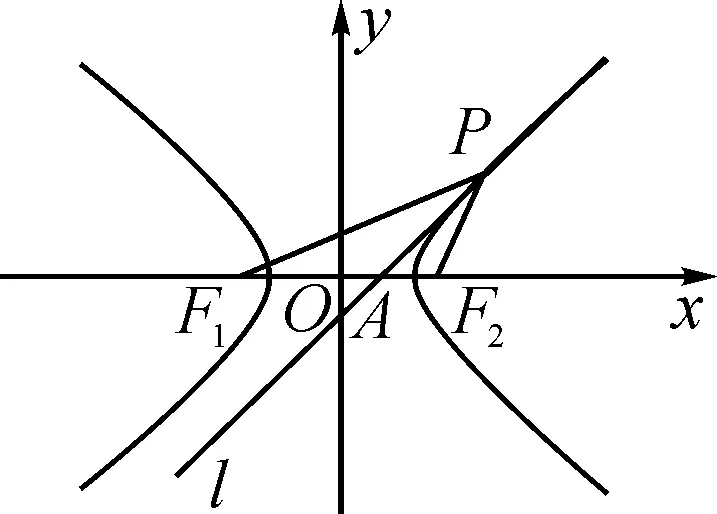
圖6
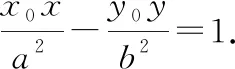
根據焦半徑公式|PF1|=a+ex0,|PF2|=ex0-a,則有
根據角平分線定理,雙曲線過點P的切線為∠F1PF2的角平分線.
根據上述定理,可命制出如下變式供大家練習.
例1已知拋物線E:y2=4x的焦點為M,若動直線l是拋物線E的切線,過點M作直線l的垂線,垂足為Q,求點Q的軌跡.
答案:直線x=0.
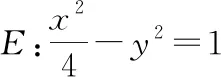
答案:|OQ|為定值,且|OQ|=2.
兩個例題的證明過程相似,現簡證例2如下:
如圖7,設直線為l為雙曲線E右支的一條切線,切點為點A,延長MQ與AF1交于點M′,根據引理4,切線l為∠F1AM的角平分線,且MM′⊥l,可得△MAM′為等腰三角形,并且點Q為MM′的中點.
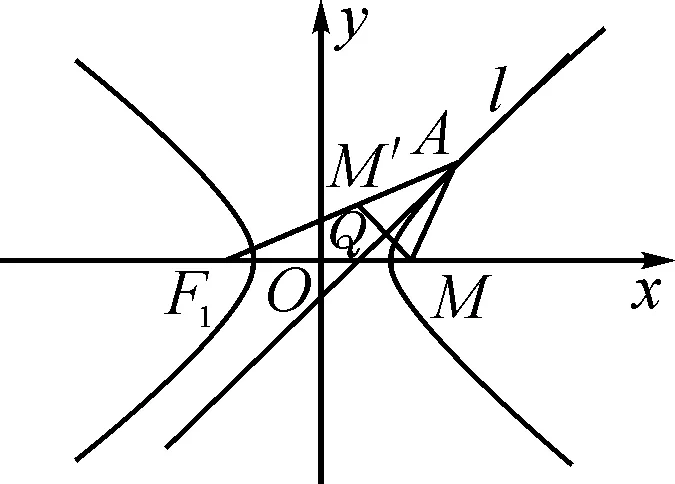
圖7
當切線l為雙曲線左支的切線時,證明方法與該證法相似,不再贅述.

