幾何條件梳理,思路突破探究
——以2021年蘇州市中考幾何綜合題為例
?蘇州高新區實驗初級中學 張 玲
1 考題再現
考題(2021年蘇州市中考數學試卷第28題)如圖1所示,在矩形ABCD中,線段EF,GH分別平行于AD,AB,它們相交于點P,點P1,P2分別在線段PF,PH上,PP1=PG,PP2=PE,連接P1H,P2F,P1H與P2F相交于點Q.已知AG∶GD=AE∶EB=1∶2.設AG=a,AE=b.
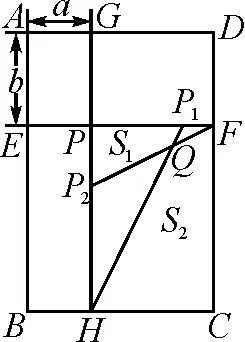
圖1
(1)四邊形EBHP的面積四邊形GPFD的面積(填“>”“=”或“<”);
(2)求證:△P1FQ∽△P2HQ;
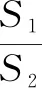
分析:此題為幾何綜合題,條件眾多,形成了矩形疊套、三角形與矩形結合,同時融合了動點.問題探究涉及到了矩形面積比較、三角形相似、面積比值分析等.問題的條件信息具有層次性,解答分析需要對條件進行梳理,具體如下.
幾何背景——矩形ABCD;
平行線——EF∥AD∥BC,GH∥AB∥CD,又EF⊥GH,將矩形分割為四個部分,也是四個矩形;
線段比例——AG∶GD=AE∶EB=1∶2,該信息隱含了矩形相似,即矩形AEPG∽矩形ABCD∽矩形PHCF,且相似比為1∶2∶3;
等線段——PP1=PG,PP2=PE;
交叉三角形——連接P1H,P2F,兩線交叉形成了眾多三角形.從圖形比例關系來看,其中必然存在相似三角形.
2 思路突破
本題目共分三問,解題時要把握問題特征,立足問題條件開展思路探究,下面逐問突破.
2.1 線段比例構建,面積大小分析
第(1)問探究四邊形EBHP和四邊形GPFD的面積關系,根據條件可知這兩個這兩個四邊形之間沒有相似關系,需要根據條件來推導線段長,然后結合公式求面積.
根據題干中的平行條件可知,四邊形EBHP和GPFD均為矩形.又知AG=a,AE=b,AG∶GD=AE∶EB=1∶2,則PE=a,PG=b,GD=PF=2a,EB=PH=2b.所以四邊形EBHP的面積=PH·PE=2ab,四邊形GPFD的面積=PF·PG=2ab,從而可知四邊形EBHP和四邊形GPFD的面積相等.
2.2 等面積轉化,相似關系構建
2.3 面積問題轉化,模型構建突破
第(3)問則是關于四邊形面積的比值問題,所涉兩個四邊形的形狀不規則,為一般四邊形.求兩四邊形面積的比值,有兩種思路:①從割補法構建模型切入,將四邊形面積轉化為幾個常規三角形面積的和,借助三角形分析面積比值;②從圖形相似入手,初步來看兩四邊形為相似關系,只需證明四邊形的四個角對應相等即可證明圖形相似,則結合相似圖形的線段比可推知面積比.基于上述方法思路,下面具體解答.
解法1:構建面積割補模型.
如圖2,連接P1P2,FH,則四邊形PP1QP2的面積可表示為S1=S△PP1P2+S△P1P2Q,四邊形CFQH的面積可表示為S2=S△FHC+S△FHQ.
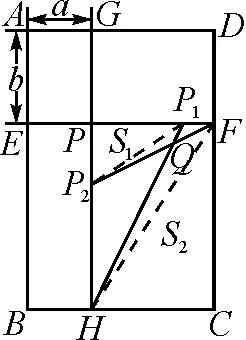
圖2
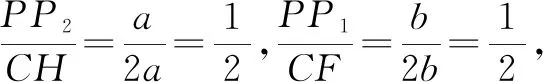
因為∠P1PP2=∠C=90°,所以△P1PP2∽△FCH.
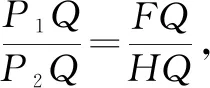
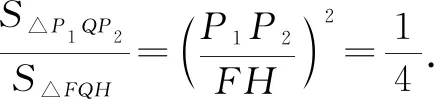
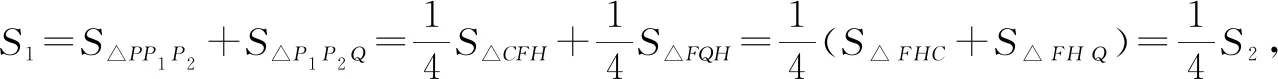
解法2:構建圖形相似模型.
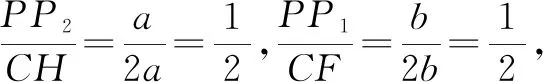
因為∠P1PP2=∠C=90°,所以△P1PP2∽△FCH.
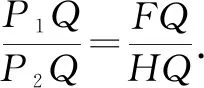
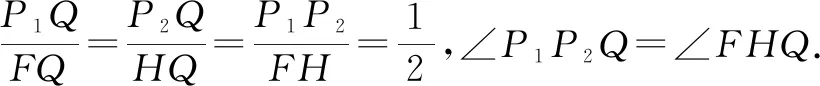
3 深度反思
上述對一道幾何綜合題進行了深入探究,從突破過程來看,線段的比例、三角形相似的知識是突破的核心,下面深入反思問題解法.
3.1 關于第(2)問的思考
第(2)問是關于三角形相似證明的問題,構建解題思路為:等面積條件轉化(四邊形EBHP=四邊形GPFD)→輔助相似三角形推導(△PP2F∽△PP1H)→問題相似三角形證明(△P1FQ∽△P2HQ).即基于第(1)問的矩形面積相等,提取關于邊長相似的比例條件,證明圖形中兩個矩形相似,進而推導出關鍵的等角——∠PFP2=∠PHP1.其中輔助相似三角形在思路構建中起橋梁作用,旨在串聯問題中的矩形條件與等角關系.同時,證明輔助相似三角形的方法在幾何證明題中十分常見.
3.2 關于第(3)問的思考
第(3)問是中考常見的面積比值問題.常見的面積比值問題有兩大背景:一是幾何圖形背景,如本題目;二是函數曲線背景,如反比例函數曲線、拋物線等.在求解面積比值時上述解法采用了兩種不同的思路,其中解法1的本質是割補思想,旨在將面積比值轉化為面積關系;而解法2的本質是相似轉化,旨在將面積比值轉化為線段長度關系.故基于不同的方法思路構建了不同的數學模型,由模型完成了面積比值求解.對于兩大背景中的面積比值問題,下面總結對應的轉化策略.
幾何圖形背景中的轉化策略:
策略1——面積公式,直接求幾何面積;
策略2——面積割補,面積比值轉化為線段比值;
策略3——相似轉化,由相似比求面積比.
函數曲線背景中的轉化策略:
策略1——底高模型,面積比值轉化為線段比值;
策略2——鉛垂模型,面積比值轉化為點的坐標參數比值.
3.3 關于問題教學的微設計
實際探究時,建議采用教學微設計的方式引導學生讀題審題,理解題意,把握知識條件來構建解題思路.以上述第(3)問的面積比值探究為例,下面開展教學微設計.
環節一:條件梳理,基礎強化
條件1:如圖2所示,在矩形ABCD中,線段EF,GH分別平行于AD,AB,它們相交于點P;
條件2:點P1,P2分別在線段PF,PH上,PP1=PG,PP2=PE,連接P1H,P2F,P1H與P2F相交于點Q.
條件3:已知AG∶GD=AE∶EB=1∶2,設AG=a,AE=b.
設問1針對條件1,可以得到哪些信息,圖中有幾個矩形?
針對條件2,P1H和P2F形成了兩組三角形△P1FQ和△P2HQ,△PP2F和△PP1H,可以得出怎樣的猜想?
針對條件3:根據線段比例,是否可以證明四邊形AEPG∽四邊形ABCD∽四邊形PHCF?若可以請求出相似比.
設計意圖:環節一旨在引導學生梳理條件,挖掘隱含信息,同時作出猜想,為后續的綜合探究作鋪墊.
環節二:設問引導,相似推導
設問2AG∶GD=AE∶EB=1∶2,根據上述條件求四邊形PP1QP2與四邊形CFQH的面積之比.
設問3請根據設問2中四邊形面積的比值關系,證明△P1FQ∽△P2HQ.
設計意圖:環節二主要引導學生從線段比值中推導面積關系,利用面積關系完成比例線段提取,進而證明三角形相似.其中思維線索“線段比例→面積關系→相似關系”是探究的關鍵.
環節三:深入探究,面積比構建
連接P1P2,FH,如圖2所示,對于四邊形PP1QP2與四邊形CFQH,若∠QHC=∠QP2P,∠QFC=∠QP1P,則可證兩三角形相似.
設問4請根據△P1FQ∽△P2HQ的性質條件,證明△P1QP2∽△FQH.
設問5是否可以結合上述相似三角形的對應角相等,證明四邊形PP1QP2與四邊形CFQH相似?
設問6請根據四邊形PP1QP2∽四邊形CFQH,求出這兩個四邊形的面積比.
設計意圖:環節三設計的核心是幫助學生掌握四邊形相似的證明思路,即“四邊形分割→相似三角形證明→四邊形相似證明”.
4 教學建議
幾何綜合題常作為壓軸題在中考數學試卷中出現,問題條件的處理方法,以及思維推理的構建過程在解題中十分重要,也是教學的重點.下面提出幾點教學建議.
(1)把握背景,條件串聯.幾何綜合題的問題條件具有層次性,往往立足圖形特征來串聯條件,實現了條件之間的交叉融合.而在實際解題時建議對問題的條件進行梳理,厘清條件之間的聯系.梳理時需要關注以下幾點:一是背景圖形的特征,以及特殊圖形;二是動點或不確定的點所在線段及軌跡;三是提取三角形以及其他幾何圖形.
(2)轉化分析,思路引導.問題條件的轉化是破解幾何綜合題的核心方法,即對問題或條件進行轉化,然后構建思路.解題教學中不能僅注重方法的講解,還要重視思維的引導;應將問題的推理過程、思路的構建過程作為重點;引導學生理解題干信息,初步處理條件,合理轉化問題,利用解題策略探索思路的構建過程.

