踐行深度學習 提高核心素養

蘇州高新區實驗初級中學 康 聰

1 引言

數學教育家波利亞指出：“教學生思考”意味著數學教師不只是傳授知識，還應該努力發展學生運用所學知識的能力.數學教育從關注“基礎知識”“基本技能”和“基本思想方法”的“三基”，轉向了“四基”，開始重視學生學習數學的“基本活動經驗”，這無疑對教師的課堂教學水平提出更高的要求.

提高學生的核心素養是一個長期的過程.在教學中，教師需要精心設計課程，研討具有研究價值的問題供學生參與互動.本文采用蘇教版教材，對教學內容的設計與改進提一點筆者的想法，以教學片斷呈現，供讀者參考.

2 “銜”——整合知識脈絡，順應思維發展

教學片段1：線段、射線、直線.

數學內容的學習是連續的，教師教學要注意學習內容的銜接，不能在初中階段故步自封.線段和角是最簡單的幾何圖形，是組成復雜圖形的基本元素.學生在小學時已經學習過線段、射線、直線的相關內容，以舊知為立足點，抓住知識的來龍去脈，本節以蘇教版七年級上冊第6章“平面圖形的認識(一)”的第一節“線段、射線、直線”為例.

師：相信同學們對這個課題并不陌生，在小學里，你學習過相關的哪些內容呢？

生1：線段有兩個端點，有固定長度，可以測量；射線有一個端點，可以向一邊無限延長；直線沒有端點，可以向兩邊無限延長.

師：(在黑板上板書)延長與延伸.直線向兩邊具有無限延長的特點，直線無限延長是直線的特性，稱之為直線的無限延伸性.也就是說，直線能夠向兩邊無限延伸，射線向一邊無限延伸.

剛才同學們講，線段有兩個端點，射線有一個端點，直線沒有端點.(圖1展示小學教材對應的內容.)

好，同學們說線段是可以測量的，說明線段有什么性質？

生2：可度量性.

生3：線段具有度量性，直線和射線沒有可度量性.

師：很好！(教師展示小學教材對應內容，如圖2.)

師：請同學們說明，線段、射線、直線有什么聯系呢？

生4：把線段AB延著AB方向無限延長，得到射線AB；同樣地，延長線段BA，得到射線BA；線段AB兩端都延長，得到直線AB.(圖3展示小學教材對應的內容.)

師：追本溯源，這是我們小學四年級的內容(PPT展示圖4).

圖4

教學說明：通過對小學中零散知識點的整合規范，師生互動，把“線”的區別與聯系的內容整理出來，實現教學活動有效性的提升.在“問題”的提出中，教師直接進入課程重點，本章是蘇教版七年級上冊“基本平面圖形”的起始課，是幾何入門的第一節課，同時讓學生領會幾何內容學習要經歷的“定義—表示—大小—線段和差”的抽象過程，體現整個知識發生、發展過程的完整性.

3 “探”——從式到形，拓展思維的局限

教學片段2：反比例函數的圖象與性質(1).

在整個初高中學習系統中，解析幾何始終是學生學習的難點.“以形看數”和“以數解形”等數與形的結合思想，需要教師教學設置層層遞進的教學難度，也是教學目標中基本思想與基本活動經驗積累的重要任務.下面以八年級下冊第11章第二節“反比例函數的圖象和性質(1)”的教學片段為例.

生1：圖象上的點的橫縱坐標的符號相同.

師追問：說說你是怎樣分析的呢？

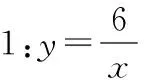
生2：x≠0，因為分母不能為0.

師：如果x，y不能取到0，說明函數圖象會有什么特點呢？

生3：x≠0，圖象與y軸沒有交點；同樣地，y≠0，圖象與x軸沒有交點.如果都取不到0，說明圖象與坐標軸沒有交點.

生4：增減性.y隨x的增大而減小.

具體地說，當x>0時，x越大，y越小；當x<0時，x越大，y越小.

師追問：你是怎樣抽象得到的呢？現在我們要具體化，例如當x>0時，舉例子說明.

教師引導(操作畫圖)：當x>0時，y隨x的增大而減小.

師：如果不討論x的范圍，從整體看，可不可以這樣描述呢？

師：非常好，請同學總結下增減性的生成過程.

生6：要具體強調在哪個象限，當x>0時，y隨x的增大而減小；當x<0時，y隨x的增大而減小.

師：很好，增減性一定要強調在哪個象限！

教學說明：教師引導學習函數的一般路徑，利用函數表達式分析兩個變量之間的符號關系，從“數”想“形”，探究出函數圖象的位置，分布在哪一個象限，進而在不同象限內，得到函數圖象的性質.在整節課中，學生自主探究，在平面直角坐標系中，對函數圖象的結構進行研究，包括取值情況與圖象分布；教師適當引導，從“模糊”走向“精確”，帶領學生初步感知圖象的分布區域和走向，利于學生思維的培養和能力的提升，從而確定函數本身的性質.

4 “歸”——鞏固知識元之間的聯系

教學片段3：直線與圓的位置關系(1).

教學是循序漸進的過程，教師要教的不僅僅是知識，更重要的是要教會學生如何思考以及解決問題的能力.在本節課前，學生已經學習過點與圓的位置關系，用圓心到定點的距離d與半徑r的大小來定義，而圓心到點的距離d是點與點之間的最近距離，即“兩點之間線段最短”.由此，直線與圓的位置關系可以怎樣判定呢，我們如何利用劃歸的思想解決新的難題？[本節是九年級上冊第2章第5節“直線與圓的位置關系(1)”].

師：請同學們用圓規在操作紙上畫出一個圓，再將一把直尺在紙上平移.如果把直尺的邊緣看作一條直線，那么在直尺平移的過程中，請把直線與圓的位置關系畫出來.

(教師通過學生畫出的圖形，展示出以下三種情況.)

現在，如何來描述直線與圓的位置關系呢？

生1：通過直線與圓公共點的個數來描述，圖5沒有公共點，圖6有一個公共點，圖7有兩個公共點.

圖5

圖6

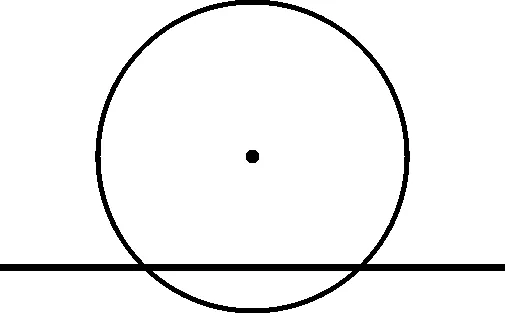
圖7

師：很好，觀察圖形，我們發現，圖5中直線與圓沒有公共點，也就是直線上所有的點都在圓外；圖6是直線上有一個點在圓上，其他點在圓外；圖7是直線上有兩個點在圓上，其余的點在圓外.我們按照直線與圓的公共點個數，來定義直線與圓的位置關系：

直線與圓有兩個公共點時，叫做直線與圓相交；(如圖7)

直線與圓有唯一公共點時，叫做直線與圓相切；(如圖6)

直線與圓沒有公共點時，叫做直線與圓相離.(如圖5)

我們知道，點與圓的位置關系，可以用d與r的大小關系進行衡量，那么，同學們是否可以用類比的思想，在直線與圓的位置關系中，也用一組對應的量來進行比較呢？

生2：可以找到直線上的點到圓心的距離與半徑r進行比較.

師：好的，請舉一個實例.

生2：例如圖8，直線上的所有點與圓心的距離都大于r.

圖8

追問：直線上有多少個點？

生(齊說)：無數個點.

師：既然有無數個點，你是否能找出一個有代表性的點刻畫與圓心距離大小的情況.關鍵是要找到什么呢？

生3：要找到圓心到直線的最近距離.

師追問：何時最短呢？

生4：垂線段最短.也就是，直線外一點到直線的最近距離，是過圓心向直線作垂線段(如圖8).

師：如圖8，也就是與哪個量之間的比較？

生5：也就是圓心O到直線的垂線段OD與r的大小比較.

師：這樣類比，我們找到了直線與圓的位置關系的數對，圓心到直線的距離d與r的大小比較.請同學們依次說出相離、相切、相交三種位置關系中，d與r的大小情況.

生6：相離?d>r；相切?d=r；相交?d

教學說明：這一環節具有思維的挑戰性，難點是引出圓心到直線的距離d.直接教學生作出圖形并不難，而學生對點與圓的位置關系認識并不深刻.點與圓位置關系的拓展，使得學生對直線與圓的位置關系的認識越來越深刻，課與課、節與節的連貫性，讓學生進入深度思考，促進數學核心素養的落實.

5 結束語

深度學習的目標是希望學生在基本數學知識學習的過程中，自主挖掘相關知識的聯系，深度理解數學本質，最終由“學會”變成“會學”.教師在課程設計中，要基于學生的學習和思維，重視對數學必備知識與關鍵能力的深度理解，立足教材，活用教材，多方位多角度思考，構建知識間的聯系與轉化，促進知識的融合，給學生實現深度學習創造良好的條件.在教學過程中，引導學生用數學的眼光觀察、分析問題，并學會用數學語言表達問題，是我們數學核心素養貫穿成功的最主要的標志.