基于GeoGebra軟件的可視化發展學生的直觀想象素養

安振亞

摘 ?要：GeoGebra軟件是一款集幾何與代數于一體的可視化教學軟件，能實現數學知識的多元表征，使靜態的數學知識靈動起來. 在數學概念的生成、定理（或公理）的發現、模型的選擇、例（習）題的解決及試題探究中，借助GeoGebra軟件的可視化能有效發展學生的直觀想象素養.

關鍵詞：GeoGebra軟件;可視化;直觀想象;教學實踐

一、問題提出

在我們生存的空間中，存在著各種各樣的事物. 當我們把眼光聚焦在事物的空間形式和數量關系上的時候，這些事物就成為數學研究的對象. 由空間事物到數學問題一般需要經歷觀察、分析、比較、歸納和抽象概括等思維過程. 這有必要借助直觀想象把空間事物圖形化，依靠幾何直觀和空間想象發現問題、分析問題和解決問題. 在這個過程中，直觀想象所引發的借形釋數、化繁為簡的思維習慣與思維方式，對學生自主學習數學甚至畢業后的工作與生活都很有價值. 既然直觀想象如此重要，那么如何才能有效發展學生的直觀想象素養呢？

數學可視化是將抽象的數學學習對象（概念原理、結構關系、思想方法等）用看得見的表征形式（圖形、圖象、動畫等）清晰、直觀地呈現出來，使人們對數學學習對象有一個形象、直觀、整體的認識和理解. 在數學教學中，借助數學可視化軟件使數學內隱部分外顯化，是提升學生直觀想象素養的有效途徑.

GeoGebra軟件是一款數學可視化教學軟件，融合幾何、代數兩大學科，實現數學知識的多元表征，賦予靜態的數學知識以靈動的動態演示與呈現，有效促進數學由科學形態向教育形態的轉化. GeoGebra軟件免費開源，操作簡單，借助其可視化，能有效發展學生的直觀想象素養.

二、發展學生直觀想象素養的實踐

在數學教學中，概念的生成、定理（或公理）的發現、模型的選擇、例（習）題的解決及試題探究等都能成為培養學生直觀想象素養的有效素材. 下面筆者談談在這些方面的一些教學實踐.

1. 概念的生成

數學概念是對數學對象共性的概括，以一種思維形式存在，可以用來判定其他數學命題是否成立，也可以作為證明其他數學結論的基礎. 要想讓學生理解數學概念，就需要教師把概念中所隱含的數學思維打開，逐步呈現給學生，讓學生在數學概念的生成過程中理解概念，把握數學概念的本質.

案例1：人教A版《普通高中教科書·數學》（以下統稱“教材”）選擇性必修第一冊“拋物線概念的生成”的教學.

在“3.3 拋物線”一節課的引言中，教師通過類比橢圓、雙曲線提出問題，并引導學生借助GeoGebra軟件來解決這個問題.

問題：動點[M]到定點[F]的距離與它到定直線[l]的距離相等時，動點[M]的軌跡是什么形狀？

實驗：如圖1，在GeoGebra軟件的繪圖區創建定直線[l]和直線[l]外的定點[F];在直線[l]上創建點[H]和過點[H]且垂直于直線[l]的直線[f];創建線段[HF]和線段[HF]的垂直平分線[m];創建直線[f]與直線[m]的交點[M]與線段[MH，MF];右鍵開啟追蹤點[M]，拖動點[H]在直線[l]上運動，觀察.

結論：動點[M]的軌跡是類似于二次函數圖象的曲線，如圖1所示.

然后，教師引導學生給拋物線下定義，并強調該定義的內涵.

感悟：GeoGebra軟件雖然能憑借可視化的實驗，生動展示拋物線的生成過程，為學生直觀地理解拋物線的定義打下堅實的基礎，但是有一點不能忽視，那就是引導學生自然想到動點[M]的構建過程.

2. 公理的發現

基本事實又叫公理，是由生活中的大量事實抽象出來的. 公理不需要證明而作為證明其他命題的依據. 公理的形成重在對事實的操作實驗和歸納概括.

案例2：基本事實3（又稱公理3）的操作實驗.

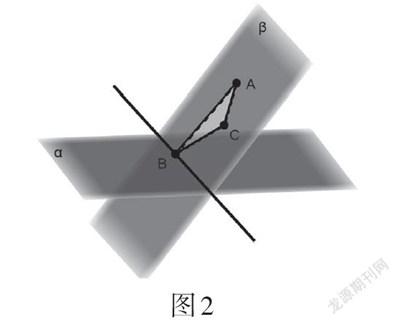
關于公理3，教材必修第二冊的第[126]頁給出了思考：如圖（圖略），把三角尺的一個角立在課桌面上，三角尺所在平面與課桌面所在平面是否只相交于一點[B]？為什么？鑒于學生的空間想象力的局限性，在教學時，教師一般會利用教具做實驗：讓三角尺的一角立在桌面上，將一張紙沿著三角尺面滑向桌面，讓學生觀察紙的下邊緣與桌面的接觸情況. 進而得到結論：兩個不重合的平面有一個公共點，那么它們有且只有一條過該點的公共直線. 該操作雖然直觀地演示了一個平面“穿透”另一個平面的動態過程，但是由于客觀因素的存在（如紙張的大小是有限的、紙張的下邊緣是否能保持與桌面平行等），直觀有余而效果達不到最優. 借助GeoGebra軟件開展可視化實驗，能給學生帶來不一樣的感受.

實驗：如圖2，在平面[α]內創建點[B]，在平面[α]外分別創建點[A，C];創建[△ABC];過點[A，B，C]創建平面[β];創建平面[α]與平面[β]的交線，該交線過點[B]. 拖動點[A，B，C]，改變三角形的形狀，觀察.

結論：平面[α]與平面[β]始終存在一條過點[B]的交線，如圖2所示.

感悟：直線與平面是通過實際事物抽象出來的幾何圖形，其形狀雖然可以用線段與平行四邊形表示，但是它的完整形態主要還是借助空間想象來完成. 而GeoGebra軟件憑借強大的[3D]功能，能夠把三維空間的事物呈現出來，豐富學生的空間想象，進而有效理解問題.

3. 模型的選擇

數學模型是從實際問題中抽象出來并用來解決實際問題的，體現了數學的工具性作用. 然而，數學模型的構建，牽涉的因素往往較多，僅僅靠紙筆運算來處理很難達到應用的教學效果.

案例3：某公司為了實現[1 000]萬元利潤的目標，準備制定一個激勵銷售人員的獎勵方案：在銷售利潤達到[10]萬元時，按銷售利潤進行獎勵，且獎金[y]（單位：萬元）隨銷售利潤[x]（單位：萬元）的增加而增加，但獎金總數不超過[5]萬元，同時獎金不超過利潤的25%. 現有三個獎勵模型：[y=0.25x]，[y=log7x+1]，[y=1.002x]，其中哪個模型能符合公司的要求？

問題：選擇獎勵模型的依據是公司的要求，也就是激勵銷售人員的獎勵方案. 可以用數學符號表示為[10≤x≤1 000，0≤y≤5，y≤0.25x.] 這三個函數哪一個符合上述約束條件呢？該問題涉及的函數較為復雜，數據處理較為煩瑣，不借助信息技術很難達到應有的教學效果.

利用GeoGebra軟件可以解決三個方面的問題.

（1）構造圖象，直觀判斷哪一個函數模型符合公司的要求.

輸入[y=0.25x]，[y=log7x+1]，[y=1.002x]，再輸入[x=][10]，[x=1 000]，[y=5]，把“[x]軸[∶][y]軸”設置為“[100][∶][1]”，如圖[3]所示. 再把繪圖區改為“標準視圖”，如圖[4]所示.

說明：通過該操作可以直觀判斷模型[y=0.25x]和模型[y=1.002x]不符合公司的要求，模型[y=log7x+1]符合公司的要求.

（2）構造交點，輔助代數運算.

用交點工具創建函數[y=1.002x]的圖象與直線[y=5]的交點[A805.52，5]，函數[y=log7x+1]的圖象與直線[x=1 000]的交點[B1 000，4.55]，如圖5所示.

說明：通過該操作可以得到存在[x0∈805，806]，使得[1.002x0=5]. 當[x>x0]時，[y>5]. 排除函數[y=1.002x]. 由于函數[y=log7x+1]是增函數，且[log71 000+1≈4.55<5]，說明函數[y=log7x+1]滿足條件[y≤5].

（3）構造圖象，運用CAS運算，確定[y≤0.25x].

打開繪圖區[2]，輸入[gx=log7x+1-0.25x]，如圖6所示.

說明：由圖象，得函數[gx=log7x+1-0.25x]在區間[10，1 000]上單調遞減，[gx≤g10]，只需判斷[g10≤0].

打開CAS運算區，計算[g10=log710+1-0.25×][10≈-0.32<0].

說明：由[gx≤0]，得[log7x+1≤0.25x]，故當[x∈][10，1 000]時，[y≤0.25x]. 這說明按[y=log7x+1]獎勵，獎金不會超過利潤的25%.

感悟：數學教學應該注重信息技術與數學課程的深度整合，實現傳統教學手段難以達到的效果. 就該案例而言，有兩處是傳統教學手段不易解決的問題：一處是畫圖不準確;另一處是求近似值有困難. 例如，計算[log1.0025]，[log71 000+1]，[g10]. 正是這個原因，造成了該案例成為實際教學中食之無味的“雞肋”：要么不講，安排學生自己閱讀;要么給學生簡單提示. 這樣做就白白浪費了它在培養學生數學建模、直觀想象等素養方面的育人價值. 而借助GeoGebra軟件豐富的構圖功能，能夠為學生提供幾何直觀，進而做出合乎情理的判斷. 當然，數學是“講道理”的，利用GeoGebra軟件得到的只是初步的判斷，要想給出令人信服的結果，還需要嚴格的代數推理（運算）來論證. 而GeoGebra軟件自身攜帶的運算區CAS能為代數運算提供強大的技術支持，讓師生不再為計算而頭痛.

4. 例題的解決

人教A版數學教材在部分章節中設置了數學在物理中的運用. 這些內容體現了數學是解決物理問題的工具，可以作為培養學生數學素養的材料.

案例4：教材必修第二冊第[40]頁的例[3].

在日常生活中，我們有這樣的經驗：兩個人共提一個旅行包，兩個拉力的夾角越大越費力;在單杠上做引體向上運動，兩臂的夾角越小越省力. 你能從數學的角度解釋這種現象嗎？

思考1：以共提一個旅行包為例，要解決問題，我們需要弄清楚兩個拉力的合力、旅行包所受的重力及兩個拉力的夾角之間的關系. 設作用在旅行包上的兩個拉力為[F1， F2]，夾角為[θ]，合力為[F]，所受的重力為[G]. 由力的平衡和向量的平行四邊形法則，可以知道[F=G]，[F=F1]+[F2]. 其中[G]為定值. 我們借助GeoGebra軟件來研究當夾角[θ]變化時[F1， F2]的大小變化情況.

實驗1：如圖7，當[F1=F2]時，在繪圖區構建向量[AB=][G]，用旋轉工具構建向量[AB]的相反向量[AB=F];創建滑動條[α]，范圍為[0， π2]，增量為[0.002]. 用定值角度工具創建角[β=γ=α];以線段[AB]為對角線、以角[β，γ]的一邊為方向作平行四邊形[ACBD];創建向量[AC=F1]，[AD=F2];在繪圖區[2]中輸入[α，k]，其中[k=F1]，右鍵開啟跟蹤;拖動滑動條[α]，觀察.

結論1：夾角[θ]越大，拉力越大;夾角[θ]越小，拉力越小;當[θ=0]時，拉力取最小值，如圖7所示.

問題：若兩個人的身高不同，手臂長也不同，則兩個人的拉力如何？

思考2：由于兩個人的身高與手臂長不同，因此兩個拉力與合力[F]的夾角不同，那么問題就轉化為：在合力一定的情況下，當夾角不同時，兩個拉力的大小變化情況如何？

實驗2：與實驗[1]類似，滑動條[α]不變，拖動滑動條[β γ=β]，如圖8所示;然后，滑動條[β]不變，拖動滑動條[α]，如圖9所示.

結論2：當一個分力與合力的夾角不變時，另一個分力與合力的夾角越大，兩個拉力也越大;夾角越小，兩個拉力也越小.

感悟：利用GeoGebra軟件開展可視化實驗，可以為學生探尋到直觀的結果，為進一步用代數方法驗證結果指明了方向.

5. 試題探究

高考數學試題以數學知識為載體考查學生的數學知識、能力與素養，進而為高校選拔人才服務. 解高考試題可以鞏固相關數學知識，查漏補缺，幫助學生形成較為完整的知識結構體系. 而探究高考試題則可以知曉試題的命制背景、考查目的，以及試題背后深層次的內容.

案例5：2020年高考數學全國Ⅰ卷理科第20題.

已知[A，B]分別為橢圓[E： x2a2+y2=1 a>1]的左、右頂點，[G]為[E]的上頂點，[AG · GB=8]，[P]為直線[x=6]上的動點，[PA]與[E]的另一交點為[C]，[PB]與[E]的另一交點為[D].

（1）求[E]的方程;

（2）證明：直線[CD]過定點.

解決該試題以后，我們會有一些疑問.

問題：如果橢圓[E： x2a2+y2b2=1 a>b>0]的左、右頂點分別為點[A，B]，點[P]為直線[l：x=h]上的動點，直線[PA]與[E]的另一個交點為[C]，直線[PB]與[E]的另一個交點為[D]，則直線[CD]是否也過定點？如果過定點，那么影響定點位置的因素有哪些呢？它與垂直于[x]軸的直線位置、橢圓的形狀是否有關？或者說定點的橫坐標與哪些參數有關？

針對這些問題，借助GeoGebra軟件進行如下實驗探究.

實驗：如圖10，在繪圖區中，創建滑動條[a，b，h];輸入方程[x2a2+y2b2=1]，創建橢圓[E];輸入方程[x=h]，創建直線[l];創建橢圓[E]與[x]軸的交點[A，B]，在直線[l]上創建一點[P];創建直線[PA，PB];創建直線[PA，PB]與橢圓[E]的交點[C，D];創建直線[CD];創建直線[CD]與[x]軸的交點[Q].

探究1：滑動條[a，b]不動，用鼠標拖動滑動條[h，]觀察點[Q]的位置是否變化;然后滑動條[h]不動，用鼠標拖動點[P]在直線[l]上運動，觀察點[Q]的位置是否變化，如圖[10]所示.

結論1：定點的位置與垂直于[x]軸的直線位置有關，即點[Q]的橫坐標與參數[h]有關.

探究2：滑動條[b，h]不動，用鼠標拖動參數[a]，觀察點[Q]的位置是否變化;滑動條[a]不動，用鼠標拖動點[P]在直線[l]上運動，觀察點[Q]的位置是否變化，如圖[11]所示.

結論2：定點位置與橢圓的長軸有關，即點[Q]的橫坐標與參數[a]有關.

探究3：滑動條[a，h]不動，用鼠標拖動參數[b]，觀察點[Q]的位置是否變化;滑動條[b]不動，用鼠標拖動點[P]在直線[l]上運動，點[Q]的位置是否變化，如圖[12]所示.

結論3：定點位置與橢圓的短軸無關，即點[Q]的橫坐標與參數[b]無關.

然后，通過證明可以得到如下性質（該性質還可以推廣到雙曲線和圓）.

性質：若[A，B]分別為橢圓[E： x2a2+y2b2=1 a>b>0]的左、右頂點，[P]為直線[l：x=h h≠0]上的動點，[PA]與[E]的另一交點為[C]，[PB]與[E]的另一交點為[D]，則直線[CD]過定點[a2h，0].

感悟：這樣一道看似平淡的高考試題，卻有著豐厚的內蘊. 借助GeoGebra軟件開展實驗探究，不僅在于探究之后獲得優美的結論，也在于探究過程中那獨有的“風景”，以及沿途領略“風景”的心情. 對于學生而言，這正是打開一扇通往“探究之路”的大門，是培養學生問題意識、探究能力和創新思維的有效途徑.

三、結束語

學生的直觀想象素養是在數學概念的生成、定理（或公理）的發現、模型的選擇、例（習）題的解決及試題的探究過程中潛移默化、潤物無聲地慢慢“生長”的，也是在直觀、想象、再直觀、再想象這樣的循環往復中逐步發展的. 借助GeoGebra軟件可以進行“形”與“數”的自由轉換，建立可見形式與抽象形式的直接聯系，滿足學生發展直觀想象素養的技術需求，幫助學生“窺視”數學的內部，推動學生的數學思維向更高層次發展，助力學生直觀想象素養的有效提升.

參考文獻：

[1]中華人民共和國教育部制定. 普通高中數學課程標準（2017年版2020年修訂）[M]. 北京：人民教育出版社，2020.

[2]岳峻，楊憶婷. 數學可視化：提升直觀想象素養的有效途徑[J]. 中學數學教學參考（上旬），2021（8）：25-28.

[3]張志勇. 高中數學可視化情境的設計原則及實施路徑[J]. 數學通報，2019，58（3）：15-19，24.

[4]岳峻. 指向數學學科核心素養的可視化教學：基于GeoGebra軟件的數學可視化實驗[J]. 中小學數字化教學，2021（8）：43-47.