水文站渠道輸水流量測驗誤差分析及優化設計
鄭玉峰
(河北省唐山水文勘測研究中心,河北 唐山 064100)
流量是江河湖庫水體變化的水文資料。為了掌握流量變化情況,要求在江河湖庫設立的水文站,根據河流水情變化特點,采用合理的流量測驗方案施測流量。我國在建的水庫水文站都肩負著渠道輸水水量的計量任務,嚴格執行《河流流量測驗規范》(GB50179—2015)(以下簡稱《規范》),不斷更新測驗設施,逐步提高測驗精度,圓滿完成輸水計量任務。為提高流量測驗精度,水文站普遍采用流速儀多垂線多測點法施測流量,控制流速從水面到河底的不均勻分布。但是多垂線多測點施測方案測驗誤差是多少,測驗精度達到何種水平,尚未進行深入的研究。隨著《規范》頒布實施,其中明確了流量測驗誤差估算和施測方案優化的具體要求。依據《規范》,對水文站渠道輸水流量測驗誤差給出了具體分析方法,以達到優化測流方案、提高測驗精度的目的。
1 流量測驗誤差
流量測驗存在的誤差是指流量測量值與其真值之差,其產生是由流量測驗方案的性質決定的。首先,流量的測量值是對計算公式中所采用的各種單項變量分別進行直接測量,在此基礎上進行計算而得出的;其次,由于測量流量的不重復性,對某一時刻某一水流狀態下的實測流量只能作一次測量,以測定相應各單項變量的值。流量測驗誤差是綜合各單項變量測驗誤差的結果。
1.1 誤差來源
采用流速儀法測流并用平均分割法計算流量時,誤差來源于下述幾個方面。
(1)起點距定位不準、水深測量方法不正確和流量測驗過程中操作不當導致的誤差,以及秒表未檢定導致的計時誤差。
(2)流速儀超期使用未檢定、流向偏角超限和上游障礙物干擾水流等導致的誤差。
(3)在流量測量斷面的每條測速垂線上,對在水深不同位置上的測點流速、有限的測速歷時引起的誤差,即測點流速受脈動現象影響所產生的誤差,在國際標準中稱Ⅰ型誤差。
(4)在流量測量斷面的每條測速垂線上,在不同位置由于測點數目不足導致的垂線平均流速計算誤差,在國際標準中稱Ⅱ型誤差。
(5)在流量測量中由于測速垂線數目不足導致的誤差,即兩垂線之間用內插方法來確定流速分布引起的誤差,在國際標準中稱Ⅲ型誤差。
1.2 誤差分類
流量測驗誤差按性質分為隨機誤差、系統誤差和偽誤差。
誤差因來源不同具有不相同的性質。測深誤差與測寬誤差由觀測的隨機誤差和儀器自身造成的未定系統誤差組成;流速儀檢定誤差由儀器檢定的隨機誤差和儀器自身在測量中所造成的未定系統誤差組成;Ⅰ型誤差為隨機誤差;Ⅱ型誤差和Ⅲ型誤差由隨機誤差和已定系統誤差組成。
《規范》規定,隨機誤差按正態分布,采用置信水平為95%的隨機不確定度描述;未定系統誤差,采用置信水平不低于95%的系統不確定度描述;已定系統誤差,應進行修正。
流量測驗中的偽誤差,即由于測驗差錯或人為粗心造成的明顯歪曲測量結果的誤差,在測量過程或數據處理中應盡可能地發現,含有偽誤差的測量成果必須剔除。
2 流量測驗誤差試驗
《規范》中流量測驗精度所作的規定是依據我國南方濕潤地區的10 余個水文站的流量測驗誤差試驗和模型試驗分析成果制定的。受自然條件和技術手段等因素限制,在我國干旱和半干旱地區尚未進行系統的流量測驗各分量的誤差試驗。對于水文站這種人工渠道斷面的流量測驗誤差,無試驗成果可供借鑒,需要開展試驗。
《規范》對不同測驗精度類別水文站的各水位分級的誤差試驗給出了具體技術要求,首先要確定水文站的站類和水位分級,以便進行誤差試驗和估算測驗誤差。
2.1 測驗精度類別和水位級的劃分
渠道輸水為水庫出口站,肩負著輸水計量任務,其流量測驗精度高低直接關系到城市生活生產主要水源的科學調度和水資源的合理配置。測站任務的重要性決定了該站要達到較高的流量測驗精度,因此確定渠道輸水水文站為一類精度水文站。
由于輸水渠道的流量受人為控制,不同于天然河道,各年最高水位相差不大,頻率計算失去意義,無法采用年特征值法劃分水位級。根據渠道的輸水能力和各年輸水流量的大小來劃分高、中、低水位,更符合實際情況。
2.2 測驗誤差試驗
流量測驗誤差試驗工作根據《規范》要求和輸水實際情況,按流量測驗誤差的來源分項進行。
測寬誤差由纜道設備自身所決定,其起點距在測流纜道主索上,測速懸索可準確置于任一位置,誤差能控制在規定范圍內。由于斷面及渠底高程無變化,每次施測流量均根據水位查算斷面,其測深誤差實際上由水位觀讀誤差所決定。因此,測寬和測深誤差不需要進行試驗,主要是試驗和估算流速測量的Ⅰ、Ⅱ、Ⅲ型誤差。試驗結合水文站原有的施測方案進行,增加測點和垂線,其布設位置應能反映測流斷面流速分布的一般規律,垂線和測點的布設控制了流速分布的變化范圍。
(1)Ⅰ型誤差的試驗應在水位穩定時進行。每次均取斷面均勻分布的4 條垂線、2 個測點測量,測點測速歷時2 000 s,每10 s 觀測1 個流速,至少試驗4次。
(2)Ⅱ型誤差試驗根據斷面流速分布情況、每次均在包括中泓在內的6 條垂線上施測,每條垂線布設11個測點,測速歷時60 s或100 s,至少試驗20次。
(3)Ⅲ型誤差試驗在輸水過程中進行,布設不少于11條垂線,用兩點法施測,測速歷時60 s或100 s,至少試驗20次。
流速測量的Ⅰ、Ⅱ、Ⅲ型誤差試驗均在水流平穩、水位無漲落變化條件下進行,試驗所用流速儀應為新檢定的儀器,性能良好。整個試驗過程中均應采用同一架儀器。試驗人員按《規范》規定操作,所取得的數據能夠滿足分析計算的要求。
3 流量測驗誤差估算
流量實際測量值為一間接測量值,其誤差是由各單項分量的誤差綜合而得到的。因此,估算流量測驗誤差首先要分別估算各有關分量的測量誤差。水文站采用纜道流速儀法施測流量,纜道的定位精度使得測寬和測深誤差控制在《規范》允許范圍內,而流速儀檢定誤差由檢定單位所決定,應在《規范》規定范圍內,這里主要根據誤差試驗結果來估算流速測量的Ⅰ、Ⅱ、Ⅲ型誤差。
3.1 Ⅰ型誤差
Ⅰ型誤差性質記述如下:隨水深和垂線位置而變化;隨流速而變化,一般是隨流速減少而增大;隨測速歷時增加而減少。Ⅰ型誤差是隨機誤差,采用置信水平為95%的隨機不確定度來描述。
對Ⅰ型誤差試驗階段取得的測速歷時為10 s的原始流速測量系列進行整理,繪制流速脈動過程線發現偽誤差和不穩定因素,并將其剔除。根據拉依達準則,對于某個殘差大于測量系列3 倍標準差的測量值,認為含有偽誤差,予以剔除。剔除壞值后的測量系列更具有代表性。
3.1.1 測點的Ⅰ型相對標準差估算
不同測速歷時的測點Ⅰ型相對標準差,使用原始測量系列的標準差和自相關函數按下列公式估算:

式中:t0為原始測量時段(s);n為原始測量時段倍數;S(nt0)為測速歷時為nt0的測點Ⅰ型相對標準差(%);S(t0)為原始測量系列的相對標準差(%)為時段位移為i的原始測量系列的自相關函數;Vj為原始測量系列中第j個測點流速值(m/s);Vi+j為原始測量系列中第i+j個測點流速值(m/s)為原始測量系列的算術平均值(m/s);N為原始測量系列的樣本容量。
采用置信水平為95%的隨機不確定度描述Ⅰ型誤差,即:
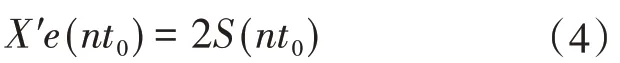
式中:X'e(nt0)為測速歷時為nt0的測點Ⅰ型隨機不確定度(%)。
3.1.2 垂線的Ⅰ型相對標準差估算
測速垂線平均流速的測量應采用有限測點和有限測速歷時實際測量,得出垂線平均流速。流量計算規則造成的系統誤差和由流速脈動造成的隨機誤差,后者即為垂線的Ⅰ型誤差。對于垂線上的Ⅰ型相對標準差,根據垂線平均流速計算公式和誤差的傳遞公式由測點計算到測速垂線上,其計算公式為:

式中:Sei(nt0)為測點測速歷時為nt0的第i條垂線的Ⅰ型相對標準差(%);p為用以確定垂線平均流速的垂線測點數;dk為確定垂線平均流速時測點流速的權系數;Sk(nt0)為測點k處的測速歷時為nt0的Ⅰ型相對標準差(%)。
3.1.3 斷面的Ⅰ型相對標準差估算
斷面的Ⅰ型相對標準差,按下式估算:
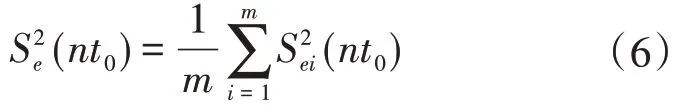
式中:Se(nt0)為測點測速歷時為nt0時的斷面Ⅰ型相對標準差(%);m為用以確定單次流量Ⅰ型誤差的測速垂線數。
3.2 Ⅱ型誤差
測速垂線上的平均流速測量按規范采用有限測點進行施測,經過計算得到垂線平均流速,通常由于經過計算規則所造成的系統誤差與隨機誤差,即為Ⅱ型誤差。估算Ⅱ型誤差,首先要對試驗資料進行整理分析,確定垂線平均流速的真值和實際計算的垂線平均流速。采用11 點法計算的垂線平均流速作為其近似真值,將少點法計算的垂線平均流速除以近似真值,得到相對平均流速,采用下列公式估算Ⅱ型誤差:
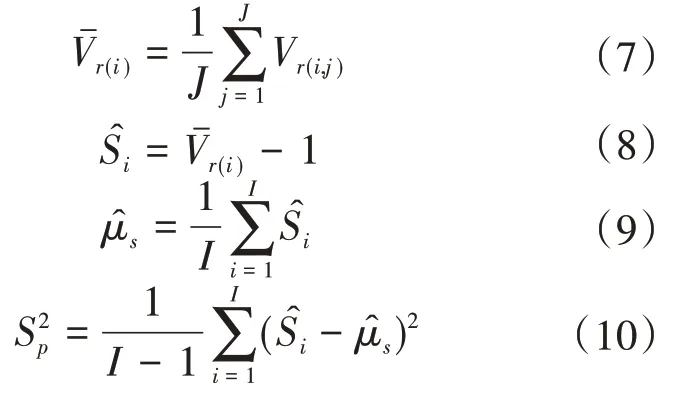
3.3 Ⅲ型誤差
測流斷面上的垂線數目數量是造成單次流量測驗誤差的主要因素,因此采用多垂線少測點的方法進行Ⅲ型誤差試驗,一般不少于10條垂線。對試驗資料進行整理分析,按平均分割法計算流量,根據斷面實際情況以11條垂線計算的流量作為近似真值。根據斷面形狀及流速橫向分布特點,遵從水文站目前的垂線布設方法,將現有垂線作為保留垂線,按均勻抽取原則,精簡一定數目的垂線,經計算得到少垂線法流量。即去掉2 條垂線,得到9 線法流量;繼續去掉2 條垂線,得到7 線法流量;再去掉2 條垂線,得到5線法流量。從斷面中抽去垂線,算得各次流量的近似真值和少線法流量,按下列公式估算Ⅲ型誤差:
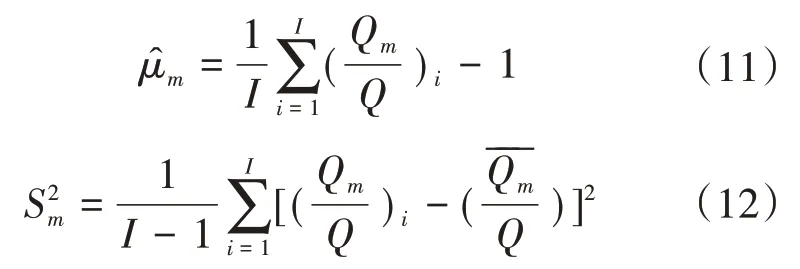
3.4 測寬、測深和流速儀檢定誤差
水文站流量測驗設施一般為水文纜道,起點距最小刻度都能滿足0.1 m,測寬的定位誤差都能控制在0.1 m之內,按垂線間距不少于0.5 m計算,測寬的隨機誤差應控制在2%以內,并且無系統誤差。
由于斷面固定不變,測深誤差主要來自水位觀測,水文站的校核水尺應裝有靜水設施,起伏度小,保證了水位的觀測精度。
流速儀鑒定誤差由鑒定單位控制,水文站只需按規定保養儀器和及時檢定。
從不利情況考慮,上述3 項誤差均按《規范》給出的誤差上限值確定,即斷面測寬隨機不確定度X'b= 2%,系統不確定度X"b= 0.5%;斷面測深隨機不確定度X'd= 2%,系統不確定度X"d= 0.5%;流速儀檢定隨機不確定度X'c= 1%,系統不確定度X"c=0.5%。
3.5 流量測驗誤差
單次流量測驗誤差由各單項誤差之和得到,分別是總隨機不確定度、總系統不確定度和已定系統誤差。

《規范》給出一類精度水文站流速儀法單次流量測驗允許誤差:總隨機不確定度高水±5%,中水±6%;系統誤差高、中水均為-2%~-1%。
4 流量測驗方案優選
多線多點長歷時的施測方案誤差小,精度高,但是在實際流量測驗工作中,如果施測時間過長,往往水位會發生變化,也會受到其他不穩定因素影響,反而降低了測驗精度。因此,需要優選誤差小、精度高、施測時間短、減少工作量、最經濟適用的流量施測方案。優化設計流量測驗方案,按下列數學模型建立目標函數和約束條件。
以單次流量誤差最小為目標函數,其表達式為:
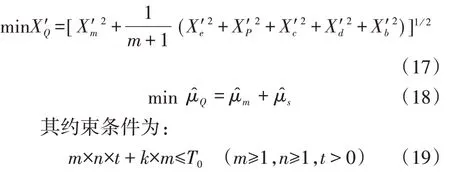
式中:m為斷面測速垂線數;n為全部測速垂線上總測點數;t為單點上的測速歷時(s);k為每條垂線所需輔助歷時(s);T0為單次測流限制歷時(s)。
5 結語
流量測驗的隨機誤差、系統誤差和偽誤差或多或少是真實存在的,根據多垂線多測點不同測速歷時的試驗資料,能夠組合出多種流量測驗方案,從中選出精度更高且經濟適用的方案。本文依托實際,嚴格執行《規范》,在保證流量測驗精度要求、滿足一次測流歷時最短的前提下,確定斷面測速數目、測點數目和測點測速歷時等之間最佳的流量測驗方案。

