基于GeoEye-1和WorldView-2遙感數據的淺海水深反演比較研究

陸天啟，吳志芳，任瀟灑，姚慧敏，邵長高

( 1. 廣州海洋地質調查局 自然資源部海底礦產資源重點實驗室，廣東 廣州 510075；2. 廣州海洋地質調查局 三亞南海地質研究所，海南 三亞 572025；3. 中國地質調查局南海地質科學院，海南 三亞 572025；4. 仲愷農業工程學院 信息科學與技術學院，廣東 廣州 510225；5. 航天宏圖信息技術股份有限公司，北京 100195)

1 引言

淺海水深是海岸環境的重要參數，其對于海洋運輸、海岸帶管理以及珊瑚礁生態保護等方面具有極其重要的意義[1]。船載聲吶測量和機載激光雷達測量等手段可以獲得準確的水深數據[2]，但因其存在耗時耗力、成本高昂以及覆蓋面有限等缺點[3-4]，使得這類方法有一定的局限性。相比之下，遙感技術具有成本低、覆蓋面廣、動態監測以及較高的空間、時間分辨率等多方面優勢[5]，特別是在淺海和偏遠的海域，已經成為傳統水深測量的有效補充手段。

半經驗半理論模型是目前常用的水深反演方法。基于水體散射的水深反演模型，經過簡化后只需回歸兩個經驗參數即可建立輻射亮度與水深之間的數據關系式，這就是經典的單波段水深反演模型[6]。通過假設不同波段在不同底質類型上的反射率比值不變，可建立雙波段水深反演模型，進而可以推廣出多波段模型[7]。在此基礎上，波段比值模型得以發展，在反演大范圍的水深時，波段比值模型更加穩定且探測范圍更深[8]。上述方法均為半經驗半理論模型，因其具有一定的物理意義和計算簡便的優點而被廣泛應用[9-10]。

多光譜遙感數據因具有較高的空間分辨率而被廣泛地應用在淺海水深反演領域。基于Landsat-TM數據，Liceaga-Correa和Euan-Avila[11]分析了主成分分析、多元線性回歸等4種水深反演方法在珊瑚礁系統中的絕對誤差。利用波段比值模型，Lu等[12]比較了Landsat-8、SPOT-6和WorldView-2 3種遙感數據在南海東鑼島海域的水深反演精度。基于多時相的WorldView-2和Landsat-8數據，Liu等[13]構建了自適應的水深分段反演模型，提高了水深反演的精度。此外，利用WorldView-3、Planet、Sentinel-2、“高分一號”等多光譜遙感數據在水深反演研究中也都取得了較好的效果[1,14-19]。GeoEye-1和WorldView-2作為當前國際上空間分辨率較高的兩種遙感數據，是多光譜遙感反演水深的常用數據源，但目前還未見對GeoEye-1和WorldView-2在同一海域水深反演能力的研究。

基于GeoEye-1和WorldView-2高分辨率遙感數據和水深實測數據，本文以南海西沙群島的羚羊礁海域為研究區，分別建立單波段模型、多波段模型和波段比值模型，選取精度最高的模型進行水深反演。在此基礎上，比較分析GeoEye-1和WorldView-2遙感數據在不同水深范圍內的反演精度，為我國熱帶島礁海域的淺海水深反演工作提供參考。

2 研究區及數據

2.1 研究區

研究區選取南海的羚羊礁海域，羚羊礁位于南海西沙群島核心區永樂環礁的西南部，隸屬于海南省三沙市，其經緯度范圍為16°26′～16°30′N，111°34′～111°37′E（圖1），為熱帶季風氣候。羚羊礁海域被珊瑚礁、海沙和水下植被覆蓋，因海域遠離大陸，受人類直接影響小，海域水體符合一類水體標準，光可穿透性強，是遙感反演水深的理想區域。

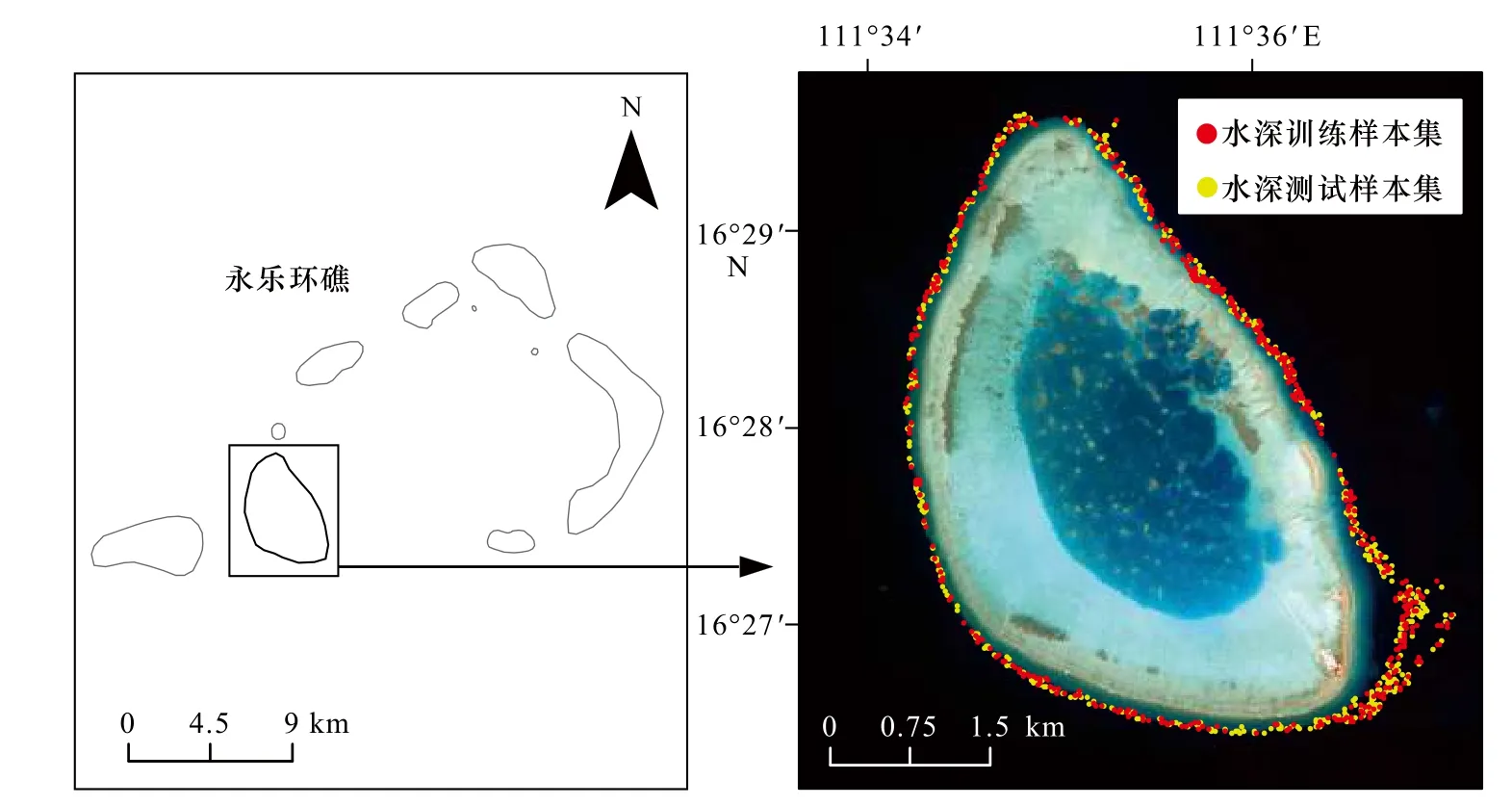
圖1 研究區及水深實測點Fig. 1 Study area and measured points

2.2 數據

研究使用的數據為美國的GeoEye-1和World-View-2遙感影像數據，GeoEye-1和WorldView-2數據均為當前世界上分辨率較高的商業遙感衛星數據，有關衛星數據的獲取時間、波長范圍及空間分辨率見表1。選取兩種數據波長范圍對應的波段進行后續的對比分析，具體為GeoEye-1的波段1、波段2、波段3、波段4與WorldView-2的波段2、波段3、波段5、波段7。

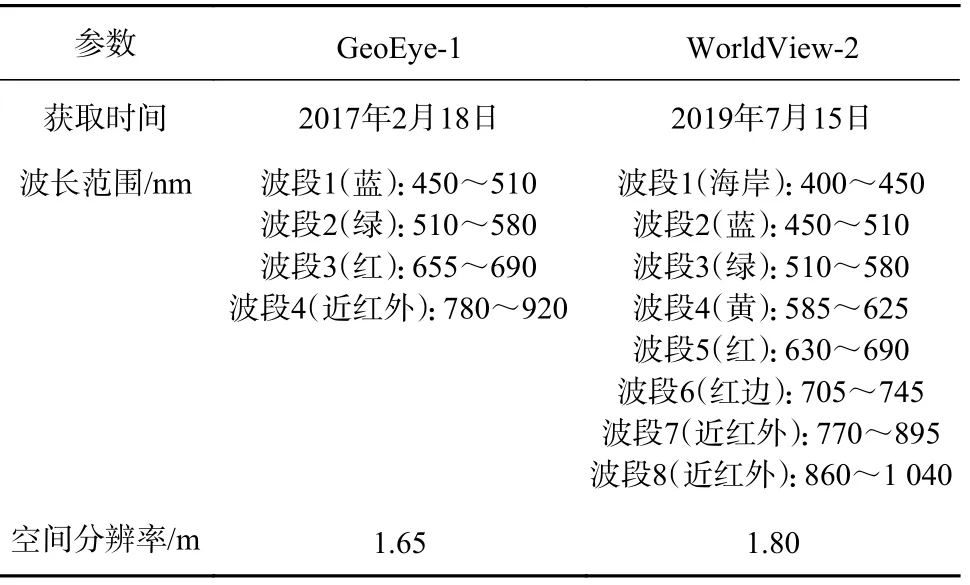
表1 遙感衛星數據參數Table 1 Remote sensing satellite data parameters

水深實測數據使用的是廣州海洋地質調查局于2019年9月利用美國Teledyne T20P型多波束測深系統獲取的水深數據，格網分辨率為20 m。由于羚羊礁海域的地質環境穩定[20]，且使用的影像獲取時間與水深實測數據獲取的時間接近，水深在一定時間范圍內變化較小，故可以適用。根據光學遙感探測水深的能力，本文篩選出羚羊礁周圍0～30 m的水深實測點，并使用ArcGIS子集要素工具將其分為訓練樣本集和測試樣本集（圖1），其中，訓練樣本集樣本440個，用來建立水深反演模型，測試樣本集樣本430個，用來分析水深反演精度。

3 數據處理

3.1 數據預處理

通常遙感影像是以像元亮度值（Digital Number，DN）的形式表現，像元亮度值是一個無量綱的整數。利用像元亮度值只能進行同景影像的相對比較，若要進行不同傳感器影像之間的定量比較和應用分析，同時一定程度上消除傳感器帶來的誤差，就需要進行輻射定標。本文采用絕對輻射定標，定標所需參數從影像的IMD（Image Metadata）定標文件中獲取。而后需要通過大氣校正的方法消除傳感器接收到的大氣等信息。基于MODTRAN 4+輻射傳輸模型的FLAASH（Fast Line-of-Sight Atmospheric Analysis of Spectral Hypercubes）大氣校正方法，可以有效消除大氣和光照等因素對地物反射的影響，其適用的范圍可從可見光至近紅外及短波紅外[21]。本文使用ENVI（the Environment for Visualizing Images）中的FLAASH大氣校正模型實現對GeoEye-1和WorldView-2影像的大氣校正，任意選取淺海中的一點，其校正前后的光譜曲線如圖2所示。

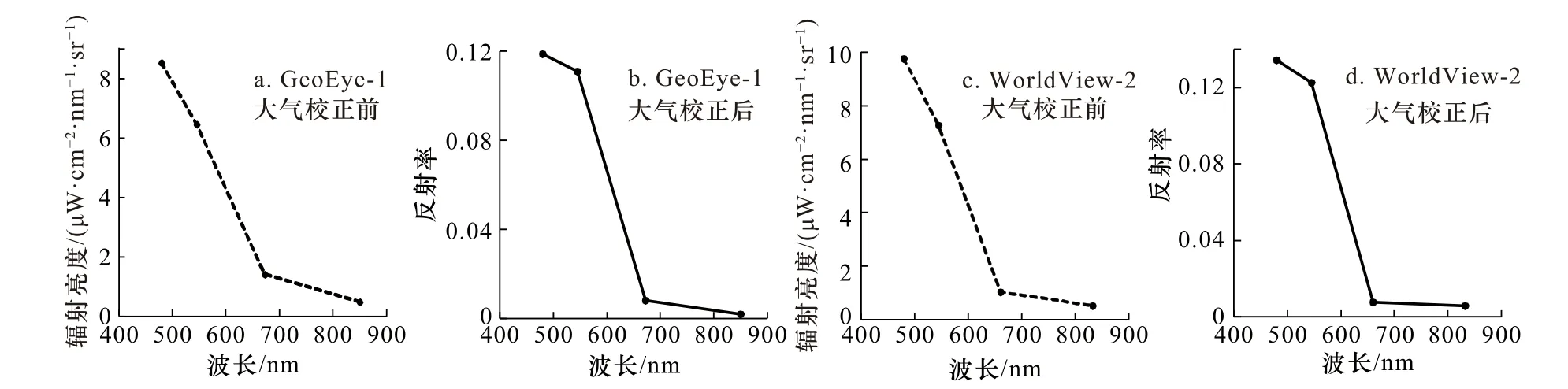
圖2 大氣校正前后光譜曲線Fig. 2 Spectral curves before and after atmospheric correction

為了使兩種不同探測器獲取的遙感影像在空間上能夠完全匹配，在由數據處理部門進行初步的幾何校正后，仍需進一步做幾何精校正。本文在兩幅影像上各選取分布均勻的30個地面控制點，通過與同區域的谷歌影像對比進行幾何精校正。

3.2 潮汐校正

海水的瞬時潮位隨著時間的變化不斷地漲落，而水深數據采集時間與遙感影像獲取時間不同，因此，為了保證影像獲取時刻的實際水深值與水深測量值之間的一致性，需要對水深測量值進行潮汐校正。根據潮汐表（https://tides4fishing.com/as/china），獲取GeoEye-1和WorldView-2成像時刻的潮高分別為0.65 m和1.74 m，同時將水深測量值轉換至潮高基準面，則影像成像時刻的實際水深值為轉換后的水深測量值加上對應的潮高。

4 水深反演模型

根據布格爾定理可知，光輻射通量隨著水深的變化呈指數規律衰減[22]。考慮到這一特性，水體表面反射率Rn可簡化為

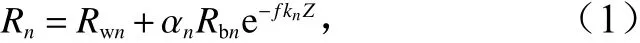
式中，Rwn為第n波段的水體反射率；αn為常量，與太陽輻射、太陽入射角和水體透過率等因素有關；Rbn為第n波段的水底反射率；f為幾何光程長度，一般情況下取常數值2；kn為水體的衰減系數；Z為水深值。公式（1）是傳統遙感水深反演常用的模型基礎，根據其可以推導出單波段模型、多波段模型和波段比值模型等多種水深反演模型[23]。

1）單波段模型

將公式（1）進行對數運算，可得：

假設海底底質反射率為常數，同時，大氣、海況和光學背景的影響相同，水體的衰減系數也為常數，令A=ln(αnRbn)/fkn，A1=-1/fkn，Xn=Rn-Rwn，則公式（2）可簡化為單波段模型的形式：

式中，Xn為第n波段的反射率。

2）多波段模型

不同類型的水體具有不同的底質反射率和衰減系數，而通過不同波段比值的形式可以一定程度上消除這些差異[7]，多波段模型在此基礎上得以發展。假設兩個波段（例如波段1和波段2）在不同的底質類型上反射率比值保持不變，即為常數，則通過對兩個不同波段對應的公式（1）進行比值運算，可得：

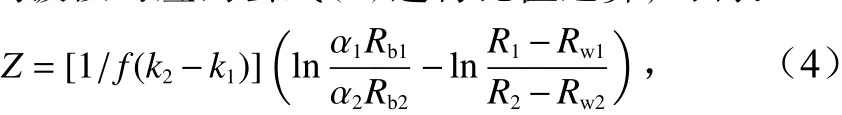
令Xn=ln(Rn-Rwn)，并按照與單波段模型相似的推導方法，可得到雙波段模型公式：

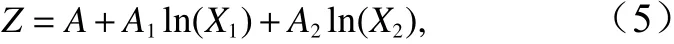
將雙波段模型進行推廣，可得到多波段模型公式：

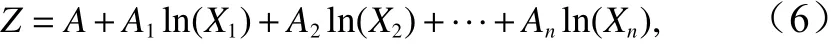
式中，An為第n波段的系數。

3）波段比值模型

波段比值模型的假設條件與多波段模型相同，即水底反射率比值不受底質類型的影響。同樣地，將兩個不同波段對應的公式（1）進行比值運算得到公式（4），令公式（4）中Xn=Rn-Rwn，則可得到波段比值模型公式：

5 水深遙感反演

5.1 水深反演模型建立

在水深反演的過程中，水深反演模型的選取直接決定著反演精度的高低。本文基于GeoEye-1和World View-2的藍波段、綠波段、紅波段和近紅外波段，根據單波段模型、多波段模型和波段比值模型3種模型的基本形式，逐一建立波段（波段組合）與水深訓練樣本集之間的擬合公式，并計算了其對應的決定系數（表2）。

表2 水深反演模型及其決定系數Table 2 Water depth inversion model and its determination coefficients

根據表2中的決定系數進一步計算不同波段（波段組合）與水深之間的皮爾遜相關系數（圖3）。從圖3中可看出，在利用兩種遙感影像和實測值所建立的水深反演模型中，不同波段（波段組合）與水深的相關性差異較大。由綠波段參與建立模型的相關系數普遍較高，其中，由GeoEye-1綠波段參與建立模型的相關系數均達到了0.749以上，9個模型達到了0.850以上，由WorldView-2綠波段參與建立模型的相關系數均達到了0.597以上，2個模型達到了0.850以上。相比于單波段模型和波段比值模型，多波段模型的相關系數整體較高，其中使用4個波段建立的多波段模型擬合度最高（圖4），其皮爾遜相關系數分別到達了0.870和0.853，因此，選用4個波段建立的多波段模型作為水深反演的最終模型。

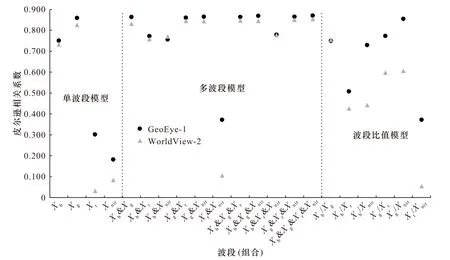
圖3 不同波段（波段組合）與水深的相關系數Fig. 3 Different bands (band combinations) and their correlation coefficients with water depth

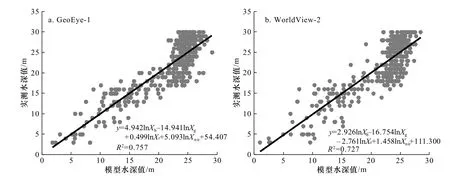
圖4 4個波段建立的多波段模型水深值與實測水深值散點圖Fig. 4 Scatter plots of multi-band model water depth value and measured water depth value established by four bands

5.2 水深反演結果

分別將GeoEye-1和WorldView-2處理后的數據帶入到4個波段建立的多波段模型中，計算后以水深5 m為間隔顯示其反演結果，如圖5所示。

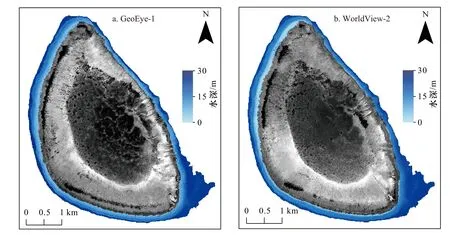
圖5 水深反演結果Fig. 5 Water depth inversion results

5.3 精度評價與分析

本文采取平均相對誤差和均方根誤差兩種指標來衡量水深反演結果的精度，其中，平均相對誤差（Mean Relative Error, MRE）為

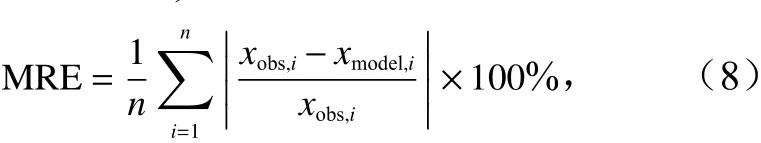
均方根誤差（ Root Mean Square Error, RMSE）為

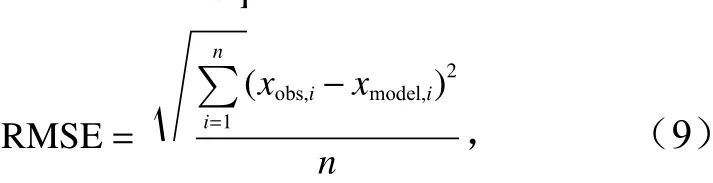
式中，n為水深測試集的點總數量；xobs,i為第i個點的實際水深值；xmodel,i為第i個點的反演水深值。

分別計算GeoEye-1和WorldView-2反演結果與水深測試樣本集在不同水深范圍內的平均相對誤差和均方根誤差（表3）。從表3中可看出，在任意水深范圍內，WorldView-2反演結果的平均相對誤差和均方根誤差均小于GeoEye-1反演結果的誤差。平均相對誤差最大值均在0～5 m水深范圍內，分別為23.43%和19.56%，其主要原因是該水深范圍處于海浪破碎帶，海水表面的粗糙度大，同時波浪破碎帶的懸浮泥沙濃度較高[24]，水體的光學衰減系數較大，導致可探測深度小，增大了反演誤差。而均方根誤差最大值均在25～30 m水深范圍內，分別為3.79 m和2.94 m。同時，整體來看，WorldView-2反演的平均相對誤差（10.40%）小于GeoEye-1的平均相對誤差（12.58%）以及其均方根誤差（2.53 m）也小于GeoEye-1的均方根誤差（2.70 m）。因此，總體而言，WorldView-2影像在研究區的水深反演能力要強于GeoEye-1影像。

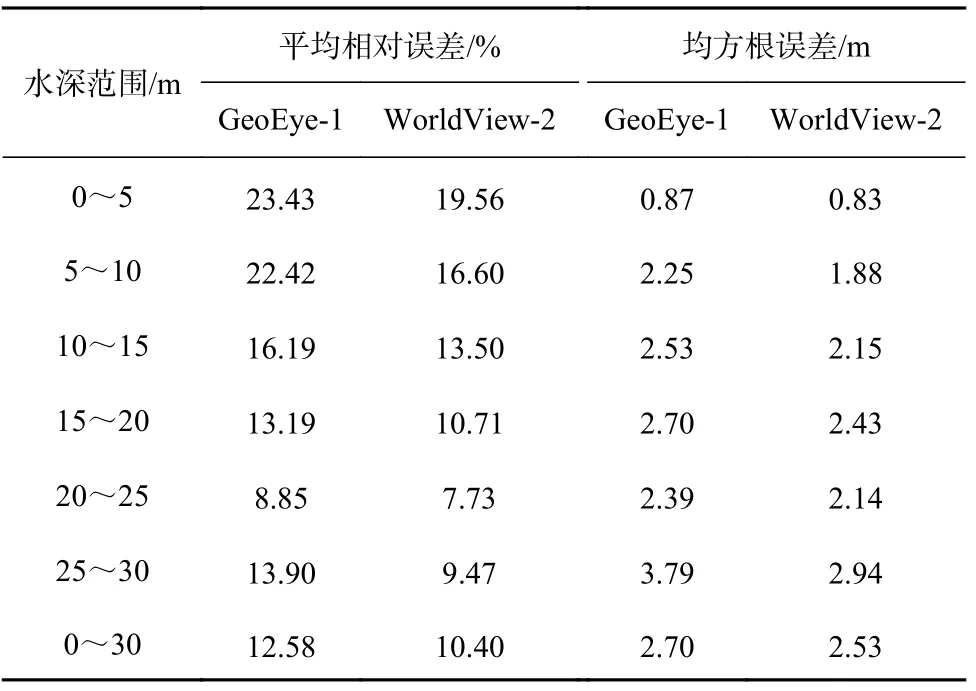
表3 不同水深范圍的反演誤差Table 3 Inversion error of different depth ranges

與此同時，兩種數據反演結果的誤差在不同水深范圍內的變化具有一致性（圖6）。在0～25 m水深范圍內，平均相對誤差隨著水深的增大呈減小趨勢，在20～25 m范圍內達到最低值，而后在25～30 m范圍內有增大趨勢（圖5a），這表明兩種數據均在20～25 m水深范圍內具有較高的反演精度。另一方面，隨著水深的增加，兩種數據反演結果的均方根誤差整體上呈增大趨勢，但與平均相對誤差變化的趨勢相同，在20～25 m水深范圍內出現了拐點（圖5b），這說明該水深范圍內的海水狀況更加穩定，更適宜水深反演模型的應用。

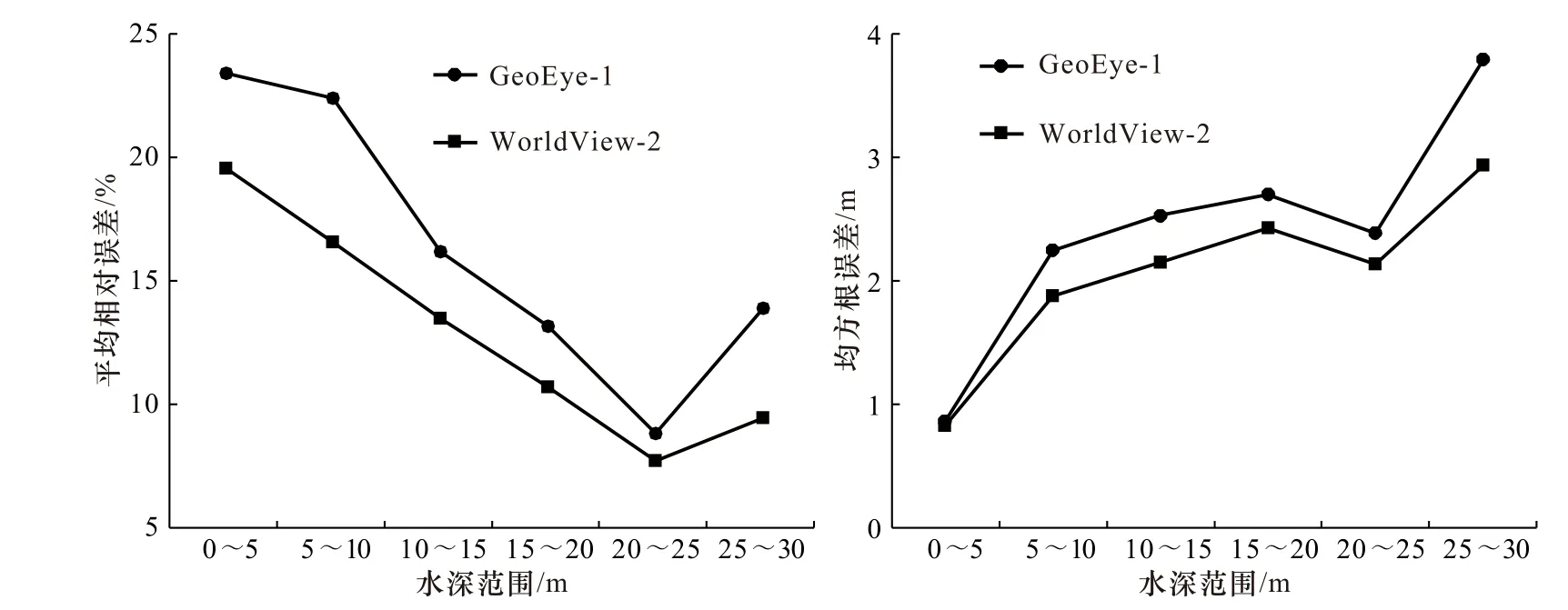
圖6 水深反演誤差變化趨勢Fig. 6 Variation trend of depth inversion error

6 結論

本文分別基于GeoEye-1和WorldView-2高分辨遙感數據及實測水深值，建立了4個波段的單波段模型、多波段模型和波段比值模型，分別選取相關性最高的模型反演了羚羊礁淺海海域的水深，并分析比較了兩種數據在不同水深范圍內的反演精度，得到以下結論：

（1）不同波段建立的水深反演模型差異較大，而由綠波段參與建立的模型相關性較高。同時，多波段模型整體上優于單波段模型和波段比值模型，特別是4個波段組合建立的多波段模型在本研究區效果最佳。

（2）GeoEye-1和WorldView-2影像的反演誤差在不同水深范圍內的變化趨勢具有一致性，其平均相對誤差均在0～5 m水深范圍內最大，而在20～25 m水深范圍內最小。隨著水深的增加，兩種數據反演結果的均方根誤差整體上呈增大趨勢。

（3）WorldView-2數據在不同水深范圍內反演結果的平均相對誤差和均方根誤差均小于GeoEye-1數據的反演結果，因此，WorldView-2影像反演水深的精度高于GeoEye-1影像的反演精度，這對于在熱帶淺海水深反演數據源的選取有一定的參考意義。

羚羊礁淺海海域大多被珊瑚礁覆蓋，底質類型較為均一，這是本文應用水深反演模型的前提條件，但嚴格意義上，研究區的底質類型是變化的，該海域底質類型變化對反演精度的影響是下一步研究的方向。另外，研究結果表明，該海域在20～25 m水深范圍內具有最高的反演精度，影響該水深范圍反演精度的因素也亟待研究，這對于提高其他水深范圍的反演精度具有重要意義。