高分影像砂質海岸線精細提取及校正方法

尹航，戚洪帥, ，蔡鋒, ，張弛，劉根，趙紹華, ，宋嘉誠, ，趙國潤,

( 1. 自然資源部第三海洋研究所 海洋與海岸地質實驗室, 福建 廈門 361005；2. 福建省海洋生態保護與修復重點實驗室，福建 廈門 361005；3. 河海大學 港口海岸與近海工程學院，江蘇 南京 210098)

1 引言

海岸帶是陸地與海洋之間的交界地帶，是地球表面最為活躍的自然區域，也是社會經濟領域中的“黃金地帶”[1]。近年來，隨著全球海平面上升[2]、河流入海泥沙銳減以及沿海開發加劇，海岸侵蝕、海岸人工化等導致海岸帶快速變化[3-4]。而海岸線的位置變遷是海岸帶演化最直觀的體現[5]，遙感手段能夠快速獲取大范圍海岸線數據，對海岸帶研究和保護管理皆具有十分重要的意義[6]。

高分辨率遙感影像是進行海岸線提取和精細化制圖的重要數據源[7]，依此提取精細海岸線數據是當前海岸帶遙感研究的熱點。遙感岸線提取的核心是對水陸邊緣像素識別與定位，現有的自動提取方法主要包括閾值分割法[8-9]、邊緣檢測法[10-11]、面向對象法[12-13]、區域生長法[14-15]等，其中以邊緣檢測法最為成熟且應用最為廣泛[16]。目前，國內外學者已使用多種邊緣檢測算子法開展遙感影像岸線提取研究，包括Sobel算子法[17]、Roberts算子法[18-19]、Canny算子法[20-22]、高斯-拉普拉斯（LoG）算子法[10]等。針對砂質海岸線提取，Kass等[23]提出了一種基于Snakes活動輪廓模型的新型邊緣檢測算法，可應用于砂質岸線的提取和平滑處理，但由于考慮參數過多致使模型較為復雜[16]；De Laurentiis等[24]提出了基于圖像紋理特征和模糊連通性的砂質海岸水邊線檢測定位方法；García-Rubio等[25]使用ISODATA非監督分類法對多光譜影像進行海陸分離，并對水邊線進行檢測提取和平滑處理；張旭凱等[26]使用改進歸一化差異水體指數（Modified Normalized Difference Water Index, MNDWI）[27]分 離水體和陸地，結合Canny算子提取得到水邊線，并進行了潮位校正。上述方法尚存在噪聲敏感性、閾值不穩定性等問題，尤其在處理空間分辨率高、背景復雜的海岸影像時，易出現噪點多、偽邊緣、岸線不連續等問題，嚴重影響岸線提取的效率和精度[6,16]。

由于遙感影像提取的岸線是衛星過境時刻的瞬時水邊線，岸灘坡度較緩的砂質岸線易受潮位影響而出現較大的位置偏移[28]。針對這一問題，Liu和Jezek[11]及馬小峰等[29]提出了基于岸灘坡度的線性潮位校正模型，Stockdonf等[30]及劉善偉等[7]則通過獲取岸灘數字高程模型（Digital Elevation Model, DEM）數據進行岸線優化與校正。然而現實中，砂質海岸海灘剖面坡度并非線性，通常是呈上凹狀的平衡剖面形態[31]。而岸灘DEM數據獲取復雜且不同時期存在變化，不具備普適性。

本文利用高分遙感影像開展復雜背景下砂質海岸線精細化提取研究，針對上述岸線提取與校正方法存在的不足，引入一種高精度、強噪聲魯棒性的結構森林邊緣檢測（Strected Forests Edge Detection, SE）算法[32]識別水邊線位置，并提出建立擬合剖面模型進行潮位校正得到海岸線，克服了傳統線性潮位校正模型誤差偏大的問題。

2 基于邊緣檢測算法的水邊線提取

2.1 結構森林邊緣檢測（SE）算法構建

SE算法是一種基于結構化學習模型的新型邊緣檢測算法，相比于傳統邊緣檢測算法，其運行速度更快、噪聲魯棒性更強、檢測精度更高[32]。

SE算法的核心是對隨機森林（Random Forest,RF）模型的訓練，RF模型是由n個不相關決策樹組成的分類器（圖1），每棵決策樹由圖像數據集S中隨機排列的數據訓練，最終預測結果通過決策樹的綜合投票得到[33]，該模型具有抗干擾能力強、抗過擬合能力強、預測精度高等突出優點[32-34]。

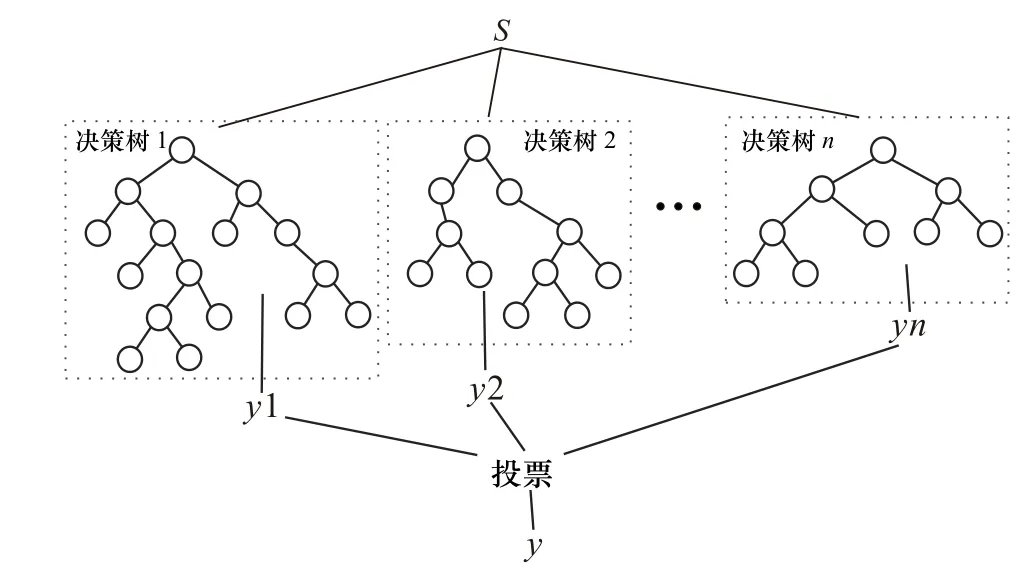
圖1 隨機森林模型示意圖Fig. 1 Schematic diagram of random forest model

使用單個決策樹對給定圖像數據集S∈X×Y進行訓練時，對x∈X（x表示圖像塊），依據量化特征，得到相應的分類結果y∈Y（y表示標簽）。對于每個節點j，其分離函數h定義為

式中，θj為增益參數；k是x的某一量化特征；τ是該特征的閾值。如果h為0，x歸類為節點j左側，如果h為1，則x歸類為節點j右側。

為使分離函數h性能最大化，定義標準信息增益，依據信息增益最大化原則確定，執行遞歸訓練：

式中，H（S）為香農熵；py為訓練數據集中圖像塊x出現標簽y的概率；SL用于訓練左節點；SR用于訓練右節點，當信息增益達到閾值時，訓練停止。

結構化學習是對映射問題的探索，其輸出結果可以是圖像、語句等復雜表示。SE算法通過將RF模型擴展到結構化輸出空間，把邊緣檢測問題公式化為在給定輸入圖像塊的情況下預測局部分割掩膜[32,35]。對于給定節點j，將該節點上的所有標簽y（y∈Y）離散化映射到離散化標簽c（c∈C），便可用c代替y計算Ij：

式中，Y為信息增益未良好定義的結構化空間；C為信息增益定義良好的離散空間；Z為使相似性度量易于計算而定義的中間空間。

以上RF模型及SE算法構建步驟詳見Breiman[34]及Dollár和Zitnick的研究[32]。

2.2 SE算法識別水邊線

使用SE算法從3個顏色、2個梯度幅值和8個梯度方向，共13個通道擴充輸入影像的每個圖像塊，檢測邊緣特征。對于32×32結構化圖像塊，使用16×16的窗口預測分割掩膜，取各個掩膜在單一像素點的平均值作為最終像素值，輸出結果是1幅灰度圖像（圖2），各像素點灰度值代表其為邊緣點的概率。

圖2 結構森林邊緣檢測算法邊緣概率Fig. 2 Edge probability of strected forests edge detection

2.3 數字化水邊線提取

為得到數字化水邊線，依據輸出結果設定閾值，將邊緣概率圖像轉化為0和1的二值圖像，在保留邊緣檢測效果的同時便于進行形態學處理。應用Arc-Scan自動矢量化方法，從柵格數據中提取邊緣線，經過后期編輯處理即可得到數字化水邊線結果。

3 岸線校正與優化

3.1 潮位校正原理

潮位校正是依據海灘地形和潮位變化關系，將遙感提取瞬時水邊線校正至一般意義海岸線（平均大潮高潮線）的過程，是基于遙感影像進行岸線精細提取的重要環節，對于砂質海岸的岸線提取尤為關鍵。常用的線性潮位校正模型原理如圖3所示：假設海灘剖面為均一的斜坡，基于不同潮時影像水邊線c1、c2推算岸灘坡度θ，計算校正距離d[26]。該模型主要缺點有兩個：（1）忽略了岸灘地形、地貌因素影響，校正距離與實際偏差過大；（2）坡度數據多來源于不同潮位時刻水邊線推算，容易引入遙感預處理誤差、解譯誤差等新誤差。

圖3 線性潮位校正模型原理（修改自文獻[27]）Fig. 3 The principle of linear tide level correction model(modified from reference[27])

3.2 平衡剖面模式

自然狀態下，砂質海岸的海灘通常發育平衡剖面，一般呈上凹形態，坡度隨向海距離增加而變緩，可使用數學模型描述其形態[31]。Bruun[36]最早提出海灘平衡剖面模式，Dean[37]將其理論化為

式中，h為當地水深；x為距海岸線距離；m為統計得到的系數；A為剖面尺度參數，與當地泥沙粒徑有關。依據Dolan等[38]對美國東海岸及墨西哥灣504條剖面觀測結果，可知m值分布符合高斯分布，期望值為2/3，研究中一般可取2/3作為m的值[39]。

3.3 擬合剖面潮位校正模型

本文為進行海岸線精細提取，考慮研究區海灘地形和潮位變化，基于實測海灘剖面數據和Bruun-Dean平衡剖面模式，建立擬合剖面模型進行潮位校正（圖4）。由于模型擬合需要衛星過境時刻潮位值及研究區多年平均大潮高潮位值，而驗潮站提供的潮位數據為當日高低潮和逐時潮位預報結果，可使用經典潮汐插值模型對衛星過境時刻潮高進行推算：

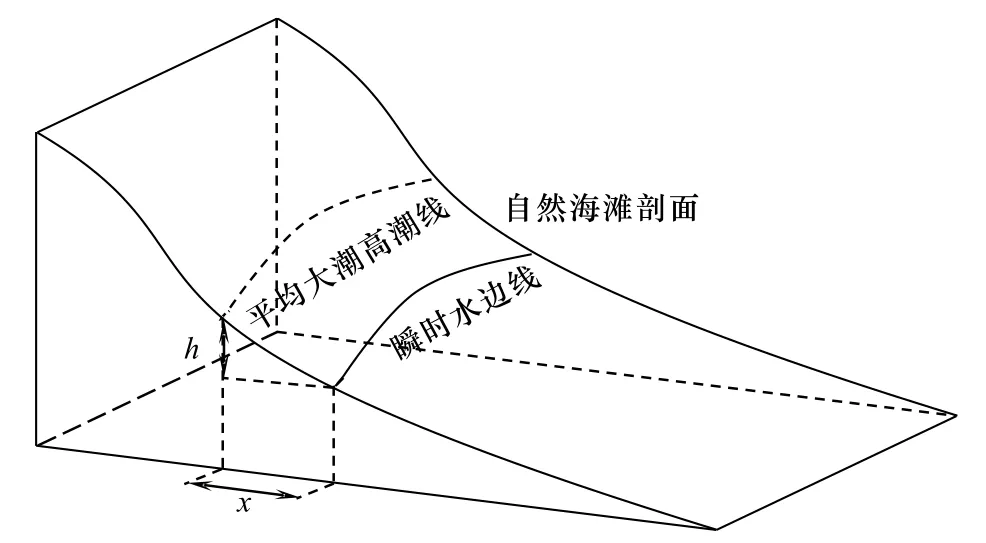
圖4 擬合剖面潮位校正模型原理Fig. 4 The principle of the tide level correction model of the fitted profile

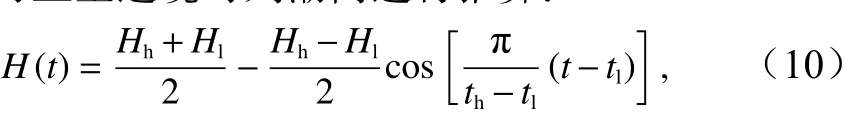
式中，t為衛星過境時刻；H為對應潮高；Hh為當日高潮潮高；th為當日高潮時；Hl為當日低潮潮高；tl為當日低潮時。

為進行數據擬合，以平均大潮高潮線作為校正后海岸線位置，將其對應高程面作為基面，對RTK設置高程和驗潮站潮位數據高程作統一調整。而后基于Bruun-Dean平衡剖面模式，使用研究區實測剖面數據進行模型擬合，公式為

式中，x為與海岸線水平距離；h為對應水深；a為剖面尺度參數；n為系數，參數a、n由數據擬合得到。通過衛星過境時刻潮高求得h的數值，代入方程即可得到瞬時水邊線相對海岸線的潮位校正距離。

4 試驗與分析

4.1 研究區域

研究區域為海南省海口市西海岸，東起秀英港、西至天尾角，海岸線總長度約12 km（圖5）。該區域海岸背景復雜，岸線類型以砂質岸線為主，剖面形態為上凹耗散型，附近建筑物密集，部分岸段在沙灘后方建有海堤。

圖5 研究區地理位置Fig. 5 Geographical location of the study area

4.2 數據源與預處理

本文使用了1景WorldView-2衛星于2019年9月23日攝取的多光譜影像，其幅寬為16.4 km，覆蓋整個西海岸區域。在進行邊緣檢測岸線提取之前，按照輻射校正-幾何校正-正射校正-影像融合的技術路線對原始影像進行了預處理。輻射校正包含輻射定標和大氣校正兩個步驟，將衛星傳感器測量值轉換為地表真實反射率；之后結合地面控制點（Ground Control Point，GCP）對影像進行幾何精校正，控制均方根誤差（Root Mean Squared Error，RMSE）在0.5個像元以內并使用基于有理函數（Rational Polynomial Coefficient，RPC）模型的正射校正法[40]，消除地球曲率、地形起伏引起的影像畸變；最后采用超分辨率貝葉斯法自動融合法[41]對多光譜影像進行數據融合。融合后的影像空間分辨率由1.85 m提升至0.5 m，在保留空間紋理信息的同時，水陸邊緣愈為清晰明顯。

本文所用的數據還包括與影像獲取時間同一季度的野外實測數據（2019年11月），包含海灘剖面數據、海岸線數據等。測量所用儀器設備為思拓力（STONEX）S9Ⅱ專業型實時差分定位移動站（RTK），控制平面精度為 -8～8 mm均方根（Root Mean Square,RMS），高程精度為-15～15 mm RMS；此外，還搜集了位于研究區域內的秀英驗潮站（站點潮高基準面在平均海平面下150 cm）2015-2019年潮位數據，用于建立擬合剖面模型，整體技術流程如圖6所示。

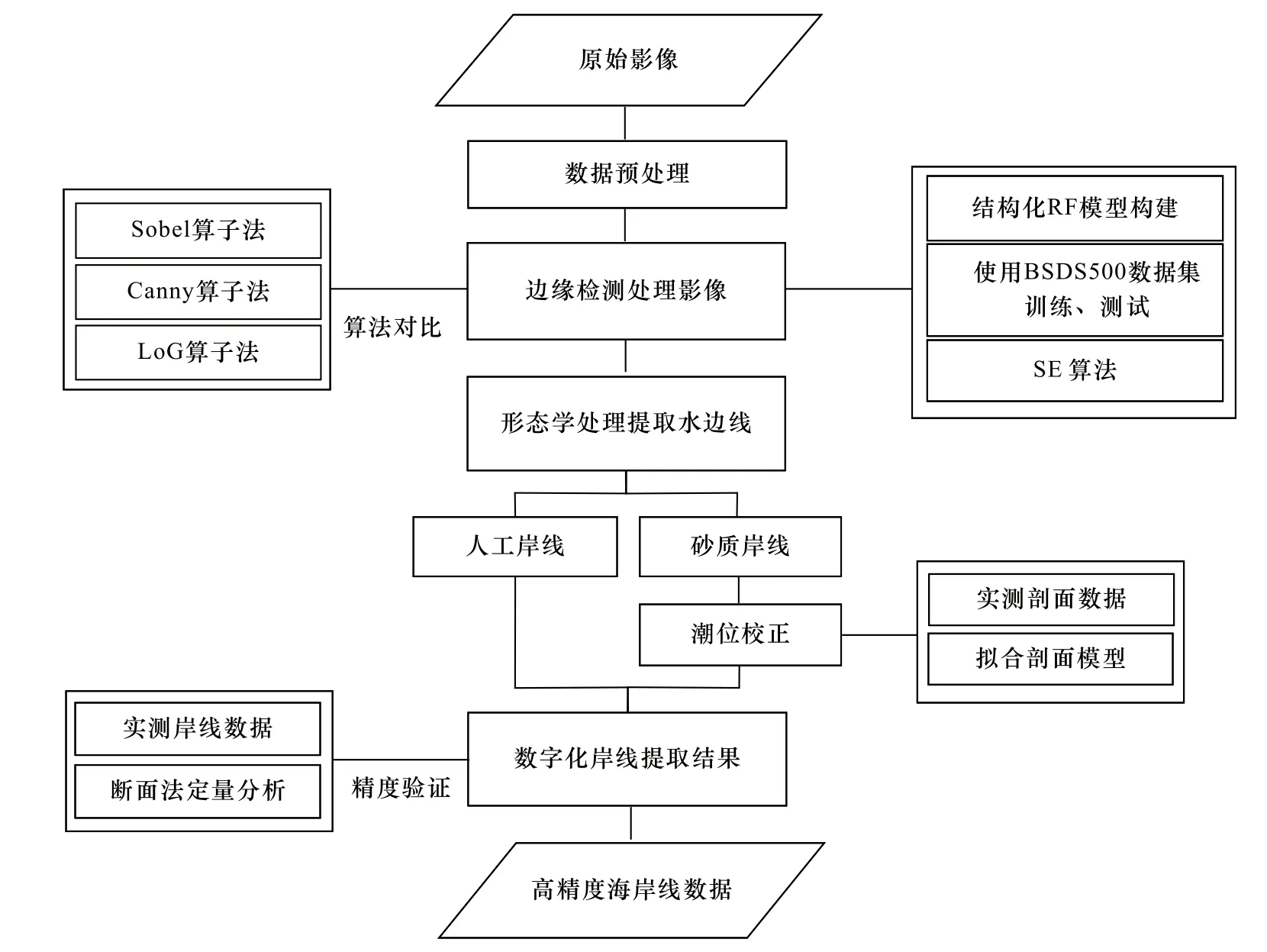
圖6 砂質岸線精細提取技術流程Fig. 6 Sandy shoreline extraction technology process

4.3 邊緣檢測算法效果與對比分析

為評估SE算法岸線識別效果，本文使用3種常用的邊緣檢測算子法（Roberts算子法、Canny算子法、LoG算子法）與之進行對比。篩選出一處研究區內背景較為復雜的岸段圖像單元，分別使用4種算法進行邊緣檢測并獲取結果（圖7）。為評估邊緣檢測質量效果，本文使用幀速率（單位：fps）、連續性（Cdr）和F值3種評價指標，對4種算法進行定量評價（表1）。其中，幀速率用于體現邊緣檢測算法的運行效率；連續性能夠反映海陸邊緣提取的完整程度；F值則為精確率與召回率的調和平均數，是定量評估邊緣檢測算法精度的常用指標[42]。

圖7 邊緣檢測算法效果Fig. 7 Edge detection algorithm effect

依據表1結果，對4種邊緣檢測算法輸出結果進行對比分析。LoG算子法輸出結果F值最低且Cdr值最低，尤其在水陸邊界處出現大量斷點，無法有效定位水邊線；Roberts算子法和Canny算子法F值和Cdr值相對較高，可用于水邊線的識別，但在噪聲水平較高的位置出現明顯邊緣斷點和偽邊緣現象；本文所用SE算法輸出結果清晰、細膩，較少出現斷點和偽邊緣現象，其評價指標F值和Cdr值在4種算法中均為最高，說明SE算法在水陸邊緣檢測精度和連續性方面效果最好。在算法運行速率方面，由于使用隨機森林模型，SE算法幀速率達到60 fps，是邊緣檢測算子法的4倍。由此可見，針對高分影像邊緣檢測，SE算法相比于傳統邊緣檢測算子法更加精準高效，適用于高分影像砂質岸線的識別和精細提取。

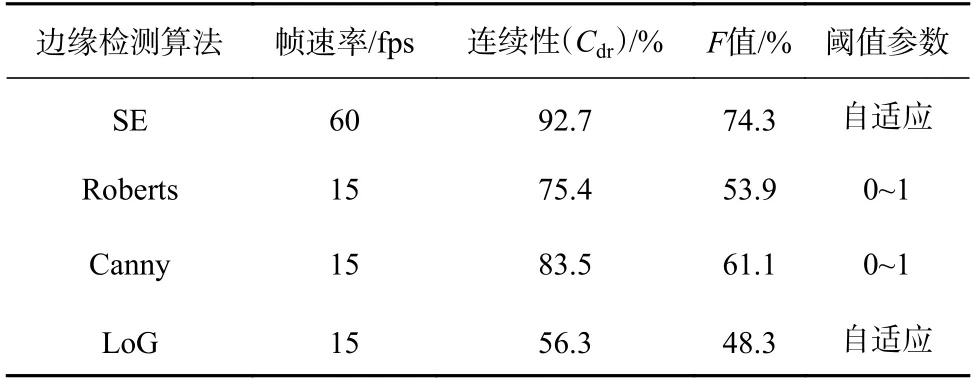
表1 邊緣檢測算法質量評價結果Table 1 Quality evaluation results edge detection algorithm

4.4 岸線提取結果與分析

4.4.1 瞬時水邊線提取

將WorldView-2影像數據輸入訓練好的SE算法模型，按2.2節和2.3節所述方法步驟提取得到數字化水邊線，結果如圖8所示。顯見，SE算法輸出水邊線結果具有高信噪比、高精度、強連續性的特點，且在算法運行過程中，不需要手動調節閾值參數，自動化程度高，具有很強的場景自適應性。

圖8 水邊線檢測結果Fig. 8 Detection results of land and water boundary lines

4.4.2 潮位校正與海岸線提取

本文使用10條研究區RTK實測海灘剖面數據，依據3.3節所述方法步驟建立擬合剖面模型：h(x)=axn（圖9a），同時建立擬合線性模型：h(x)=bx（圖9b）進行對比評估。由擬合結果（圖9）可知，擬合剖面模型參數a擬合結果范圍為0.162 8～0.206 7，期望值為0.184 7，參數n擬合結果范圍為0.653 4～0.715 7，期望值為0.682 5，與Bruun-Dean平衡剖面模式中m期望值的2/3相近；擬合線性模型參數b的擬合結果為0.083 9。

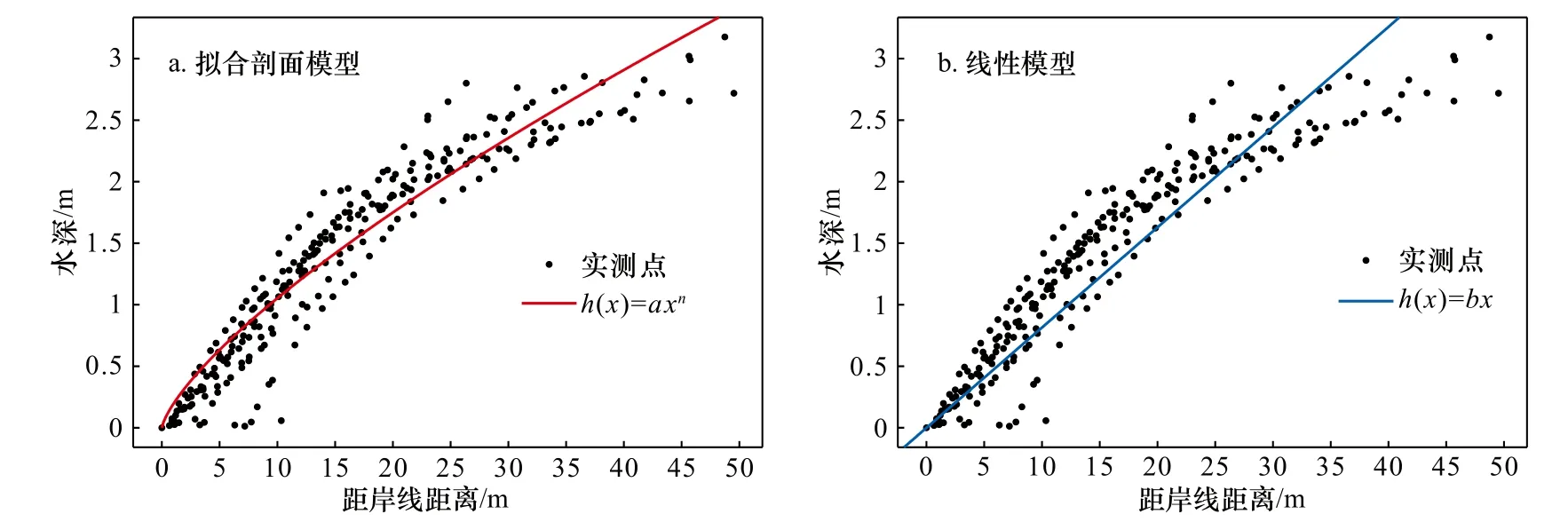
圖9 潮位校正模型擬合結果對比Fig. 9 Comparison of fitting results of tide level correction models

計算兩種模型擬合評價參數（表2），對比可知，擬合剖面模型的確定系數（R-square）為0.93，高于線性模型的0.78，說明前者的擬合優度更高。在誤差平方 和（Sum of the Squared Errors, SSE）和 均 方 根 誤 差（Root Mean Squared Error, RMSE）方面，擬合剖面模型結果值相較于線性模型都更小，說明使用擬合剖面模型進行潮位校正，預測精度更高。

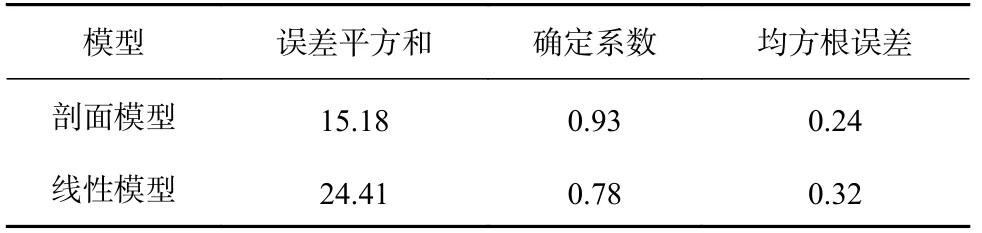
表2 擬合模型評價參數Table 2 Fitting model evaluation parameter

使用秀英驗潮站潮位數據，依據潮汐插值模型和基面高程計算水深值h。將衛星過境時刻潮位數據對應水深ht代入擬合剖面方程，求得瞬時水邊線與平均大潮高潮線（海岸線）之間的垂直距離，并依此將矢量水邊線分段沿其垂線向陸移動，最終提取得到真實的海岸線結果（圖10）。

圖10 研究區海岸線提取結果Fig. 10 Extraction results of coastline in the study area

4.4.3 擬合剖面模型分析與評估

使用擬合剖面模型進行潮位校正，相較于傳統線性模型，海岸線結果精度獲得提升；與DEM高程模型潮位校正相比，在保障精度的同時，該方法僅使用海灘剖面數據，不需要進行全地形測繪，減少了野外實測工作量。

然而，在進行大范圍、長時間尺度的砂質岸線演變研究時，建立模型所需的實測海灘剖面數據量依然較大，需對上述方法進行適當簡化。針對方程：h(x)=Axm，Moore[43]通過大量實驗數據和實地測量數據檢驗了所謂的剖面尺度參數A與泥沙粒徑D之間的相關性；而沙粒沉降遵循斯托克斯定律，泥沙粒徑D與沉降速率之間存在方程關系；Dean[44]隨后提出了基于沉降速率w下參數A與粒徑D之間的轉換關系，公式為

式中，A單位為m1/3；w單位為cm/s。為便于查詢，Dean[39]給出了參數A與泥沙粒徑D之間的對應簡表。在實際應用中，可基于研究區泥沙粒徑數據，直接建立擬合剖面模型進行潮位校正。

4.5 精度驗證與分析

4.5.1 精度驗證結果

為驗證結果精度，以RTK實測岸線數據作為參考岸線，使用斷面法對提取岸線進行定量分析。研究區岸線總長度約為12 km，以5 m為間隔布置了2 324條斷面，并將各斷面與參考岸線的2 324個交點作為參考點集（圖11）。

圖11 斷面及參考點布置圖Fig. 11 Transects and reference points layout drawing

計算提取岸線相對于參考岸線的偏移量，統計各斷面對應結果（圖12）。紅色實線為相對參考岸線0偏移位置，數據位于該線以上表示提取岸線相對參考岸線向陸偏移，位于該線以下表示提取岸線相對參考岸線向海偏移。經統計分析，提取岸線平均偏移量為2.34 m，說明提取岸線精度較高；標準差為1.22 m，說明數據離散程度較小、穩定性較強。

4.5.2 結果評價與誤差分析

根據參考點集，求得提取岸線均方根誤差為2.23 m，由于參考岸線測量精度為毫米級（詳見4.2節），說明提取岸線定位精度優于2.5 m。依據我國基本比例尺地形圖制圖標準，本文提取岸線整體滿足1∶5 000比例尺海岸帶制圖需求[1]。但由于本文所用WorldView-2影像空間分辨率優于1 m，岸線定位精度超過了兩個像元，分析誤差可能來源于以下幾個方面：

（1）波浪因素對水邊線位置的影響。同天文潮汐一樣，近岸波增水、波浪爬高等因素引起的近岸水位變化會引起瞬時水邊線的位置平移[45]。由于缺乏衛星過境時刻波浪觀測數據，本文未進行波浪校正。

（2）影像背景復雜程度對邊緣檢測算法的影響。依據圖12中數據，提取岸線相對于參考岸線最大向海偏移距離為5.33 m，最大向陸偏移距離為5.16 m。根據斷面編號定位海岸線位置，發現偏移距離較大的位置多為建筑物密集位置以及岬角、河口等復雜地理地貌單元，使得該位置岸線提取結果精度較低。

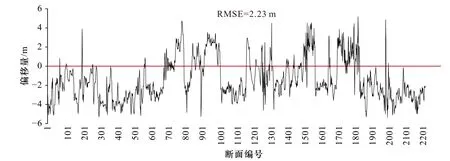
圖12 提取岸線偏移量統計Fig. 12 Extract coastline offset statistics

（3）Bruun-Dean平衡剖面模式局限性影響。本文提出的擬合剖面模型潮位校正法相比于傳統線性模型精度更高，所用Bruun-Dean模式簡明但存在參數A物理意義不明以及在破波帶以內適用性較差等局限性，與實際海灘剖面形態依然存在一定偏差。

（4）不確定性誤差累積的影響。由于遙感數據從獲取、處理、分析等一系列過程中都有不同類型和程度的不確定性引入，并在進一步分析中傳播，尤其是對于遙感岸線提取驗證等定量分析，傳感器誤差、影像校正誤差、人員誤差等不確定性累積會對數據結果精度產生更大的影響。

5 結論與展望

使用SE算法對高分辨率海岸影像進行了水邊線檢測與提取。通過與傳統邊緣檢測算子法（Roberts算子法、Canny算子法、LoG算子法等）對比研究，發現SE算法具有更高的邊緣定位精度、更強的噪聲魯棒性、更快的運行速率以及針對復雜背景海岸線識別的自適應能力。

針對線性模型誤差較大的問題，提出了基于擬合剖面模型的潮位校正方法。通過RTK實測剖面數據結合經典的Bruun-Dean平衡剖面模式，建立擬合剖面模型，提升了遙感提取海岸線優化與校正的精度。

基于同期實測岸線數據，使用斷面法對提取岸線進行了精度評估。定量分析了提取岸線相對參考岸線的偏移量，結果顯示，提取岸線的定位精度優于2.5 m，滿足1∶5 000比例尺海岸帶制圖需求。

下一步工作中，擬制作高分辨率遙感影像數據集專門用于算法的訓練和測試，并研究學習適用性更強的平衡剖面模式以及近岸波浪岸線校正方法，進一步提升岸線提取的精度和效率。