基于圖譜特征與度量學習的行星齒輪箱健康評估

李加興，陳廣艷，張魯晉，王友仁，張砦

(1. 南京航空航天大學 自動化學院，江蘇 南京 211106；2. 中國航發湖南動力機械研究所 直升機傳動技術國防科技重點實驗室，湖南 株洲 412000)

0 引言

行星齒輪箱具有較大的傳動比與承載能力，廣泛應用于直升機主減速器、風電機組等機械裝置。由于行星齒輪箱運行在高速與重載的情況下，其關鍵零部件極易發生故障，開展行星齒輪箱在線監測與健康評估研究具有重要的意義[1]。

故障特征參數提取作為健康評估中的關鍵環節，特征參數的好壞直接決定健康評估結果。張龍等[2]將時域和頻域特征組合成多域特征矢量，建立基準高斯混合模型(GMM)，以多域對數似然概率作為健康指標，實現滾動軸承性能退化評估。對振動信號進行時域或頻域分析，提取相應統計特征，是目前最常用的特征參數提取方法。然而由于行星齒輪箱振動信號具有非線性、非平穩性，且傳統的特征提取方法需要大量的信號處理知識和豐富的專業經驗，故提取有效的故障特征參數比較困難。

度量學習(metric learning，ML)是從訓練數據中學習一個度量函數，用于計算樣本間的相似度或距離。作為度量學習最常用的度量函數，馬氏距離可以很好地度量樣本間的距離。趙帥等[3]提取時域與頻域特征并降維，計算降維特征與基線數據的馬氏距離，以馬氏距離對數作為健康值用于反映滾珠絲杠健康狀態。喬美英等[4]采用在線度量學習模型對馬氏度量矩陣進行學習，提高了分類準確率和魯棒性。目前度量學習大多用于數據分類與故障檢測，在健康評估中應用較少。

RAI A等[5]提出基于自組織映射-最小量化誤差演化的滾動軸承性能退化指標，并采用軸承健康指數構建支持向量回歸模型對軸承進行壽命估計。張云超等[6]建立齒輪裂紋擴展有限元模型，對齒輪進行壽命估計。ZHANG J等[7]研究了風力發電機健康評估方法，采用高斯混合模型對正常數據建立健康基線，并采用馬氏距離計算當前狀態與健康基線的距離進行健康評估。但以上健康評估方法中健康指標(health indicator, HI)在退化過程中波動較大、單調性較差，使得健康評估存在較大誤差。

為了提高健康指標與故障嚴重程度之間的單調性與相關性，提高健康評估準確性，本文提出一種基于圖譜特征與度量學習相結合的行星齒輪箱健康評估方法。首先對行星齒輪箱振動信號提取圖譜特征；利用度量學習構建馬氏距離度量函數，并結合支持向量回歸模型實現行星齒輪箱健康評估。

1 圖譜特征參數提取

1.1 路圖信號

路圖定義為一個頂點與頂點由邊依次連接的序列。行星齒輪箱離散振動信號與路圖信號的轉換關系為：振動信號的采樣點對應路圖的頂點，振動信號的幅值對應路圖信號序列[8]。因此，路圖頂點vi與振動信號值xi(i=1,2,…,n)相對應，xi表示頂點vi的值，則與振動信號對應的路圖信號可表示為

X=[x1,x2,…,xn]T

(1)

1.2 圖譜特征參數

圖譜指標是圖矩陣特征值的函數，而最常用的圖矩陣有鄰接矩陣W和拉普拉斯矩陣L。鄰接矩陣W中每個元素wij為連接兩個頂點vi與vj邊的權值。若兩個頂點之間沒有邊連接，則wij=0。wij通常人為設定，與頂點值xi、xj有關，本文取

(2)

拉普拉斯矩陣L定義為

L=D-W

(3)

式中D為度對角矩陣，其對角元素為di=∑wij。

根據式(4)計算W和L的特征值和特征向量

Wzi=λizi
Lyi=μiyi

(4)

式中：λi、zi為鄰接矩陣W的特征值和特征向量；μi、yi為拉普拉斯矩陣L的特征值和特征向量。

本文提取的圖譜特征如表1所示。

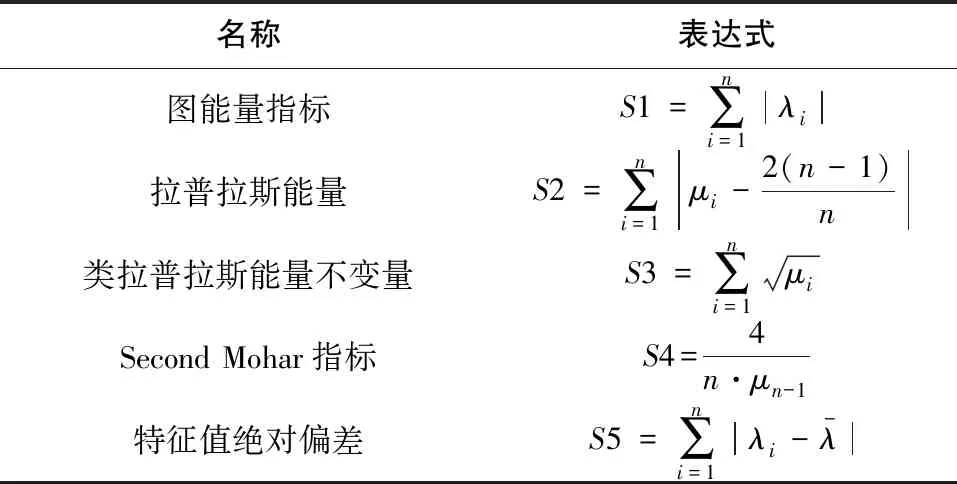
表1 圖譜特征

2 馬氏距離度量學習

2.1 馬氏距離

馬氏距離是由印度統計學家Mahalanobis提出的，可以有效計算兩個樣本的相似度。樣本x1、x2之間的馬氏距離可表示為

(5)

式中C為協方差矩陣。

采用單調性與相關性對馬氏距離進行評價，其表達式如式(11)和式(12)所示。

(6)

(7)

式中：N為馬氏距離d的數據長度；k表示故障嚴重程度。

單調性和相關性值始終處于[0,1]，越趨于1，表明馬氏距離越符合期望要求。將單調性和相關性加權平均，作為綜合評分JM，即

JM=0.5Mon+0.5Corr

(8)

2.2 度量學習

為了提升馬氏距離的單調性與相關性，引入度量學習(metric learning，ML)對馬氏矩陣M進行學習。將公式(5)改寫成如下形式

(9)

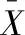
根據度量學習模型，對馬氏矩陣進行學習，即：

(10)

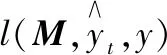
(11)

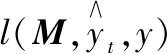
(12)

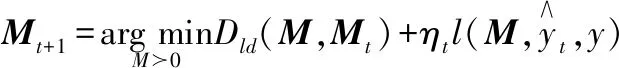
(13)

為了保證馬氏矩陣M的半正定性，ηt需要滿足

(14)

因此，馬氏矩陣度量學習過程如下：

輸入：正常狀態特征X，不同故障階段的特征Y。

a)歸一化X、Y；

b)設置初始馬氏矩陣M1=I，迭代次數N，期望損失誤差ρ；

c)Fort=1, 2,…,N；

1)使用Mt計算Y與X之間的馬氏距離d；

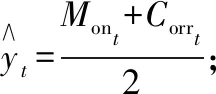
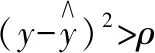
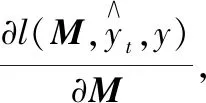
5)更新M，

6)若t=N，則退出循環，否則返回步驟c)。

輸出：馬氏矩陣M。

3 健康評估方法

3.1 基于支持向量回歸的健康評估模型

設訓練樣本

D=[(x1,y1),(x2,y2),…,(xm,ym)}]

(15)

式中：xi∈Rn；yi∈R；x為輸入樣本；y為輸出樣本。支持向量回歸函數表達式為

f(x)=ωφ(x)+b

(16)

式中：ω為權重向量；b為偏置；φ(x)為非線性映射，可以將樣本點映射到高維空間。對于參數ω和b，通過求解最小值優化問題獲得：

(17)

(18)

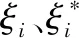
通過求解上述模型的拉格朗日方程對偶問題獲得最優解，得到回歸模型

(19)

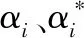
3.2 行星齒輪箱健康評估實現

基于馬氏距離度量學習與支持向量回歸(MDML-SVR)的行星齒輪箱健康評估方法實現流程如圖1所示。

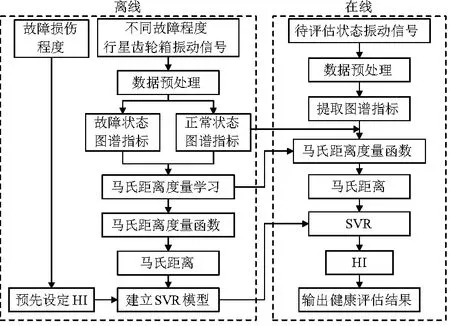
圖1 基于MDML-SVR的行星齒輪箱健康評估方法

4 實驗及結果分析

4.1 實驗方案

采用的行星齒輪箱故障模擬實驗平臺如圖2所示。該實驗平臺主要由變速驅動電機、平行齒輪箱、行星齒輪箱與磁粉制動器組成。實驗設置了共195種工況：15種轉速600～2 000r/min，13種負載0～27N·m。在太陽輪上植入了4種不同尺寸的點蝕故障，記為ds1-ds4，無故障正常狀態記為ds0，如圖3所示。4種點蝕直徑均為2mm，點蝕深度及數量見表2。根據點蝕故障面積及深度，設定故障嚴重程度分別為20%、40%、60%、80%。數據采集時采樣頻率為40 960Hz，采樣時間為25.6s。

圖2 行星齒輪箱故障模擬實驗平臺

圖3 太陽輪點蝕故障

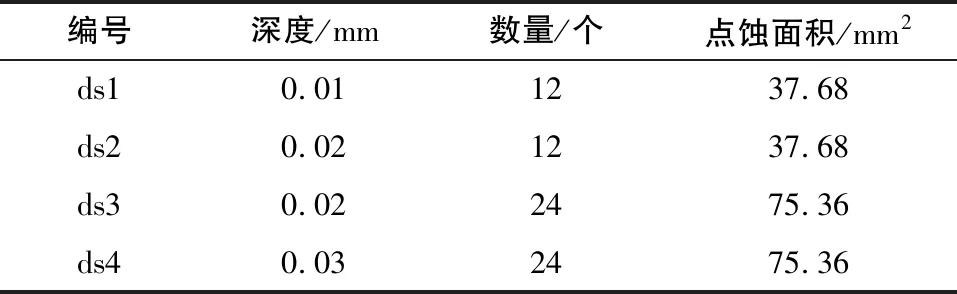
表2 太陽輪點蝕故障尺寸

4.2 振動信號特征參數

選用轉速為600r/min、載荷為6.75N·m工況下水平方向的振動信號并進行小波降噪處理，分別提取圖譜特征S1-S5。為了對比分析，提取常用的時域特征參數均方根、峰值、峭度、裕度因子，頻域特征參數平均頻率、頻率標準差。

對圖譜特征、時頻、頻域特征分別計算其隨故障嚴重程度變化的單調性、相關性與綜合評分，具體評分值見圖4。

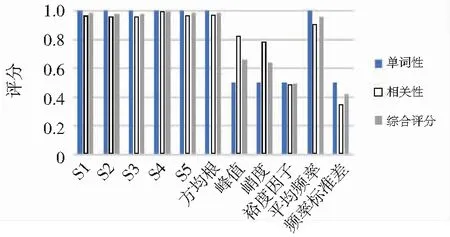
圖4 特征參數評分

圖譜指標的綜合評分普遍高于時域、頻域特征，均在0.97以上。方均根作為最常用的時域特征，其綜合評分為0.985 2，低于圖譜指標S4的0.994 7。以上分析表明圖譜指標在表征故障嚴重程度方面優于常用的時域與頻域特征。

4.3 不同健康評估方法結果比較

在每種故障程度下，取前25s振動信號，并平均分為25組，每組分別提取圖譜指標S1-S5，組成25×5的特征參數集。從25組特征參數中隨機選擇20組作為馬氏矩陣度量學習訓練數據，其余5組作為測試數據。根據度量學習步驟，設定初始馬氏矩陣為單位矩陣，對馬氏矩陣M進行訓練，從而得到馬氏距離度量函數。

采用協方差矩陣C與度量學習的馬氏矩陣M分別計算5組測試數據中不同故障嚴重程度特征參數與基準特征向量的馬氏距離，并歸一化處理，分別記為MD、MD-ML，如圖5所示。

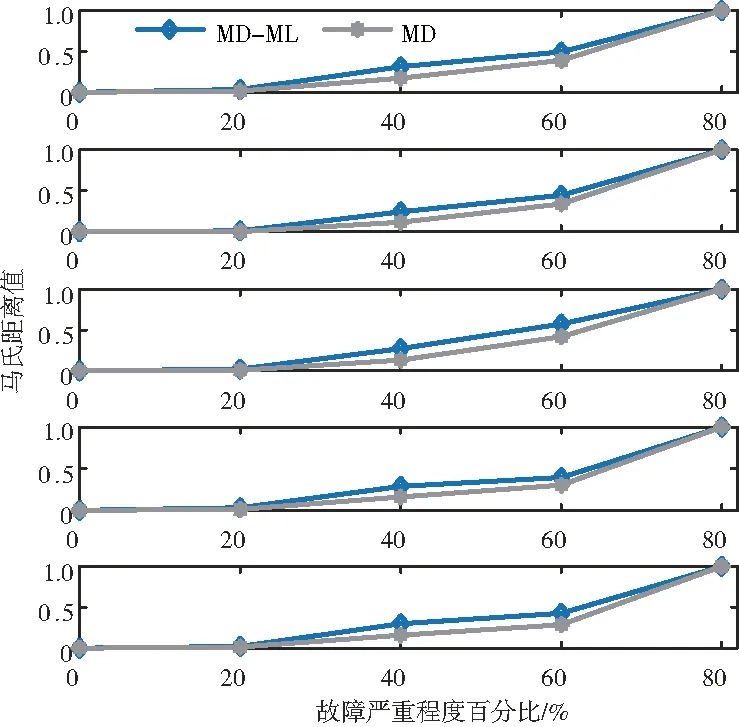
圖5 不同故障嚴重程度下的馬氏距離

從圖5可以看出兩種方法計算的馬氏距離均隨著故障嚴重程度單調遞增。為了更準確地比較度量學習對馬氏距離提升效果，采用單調性、相關性對馬氏距離進行評價，并計算綜合評分，如圖6所示。經過度量學習后，馬氏距離相關性分別提高了5.01%、5.99%、5.99%、5.49%、7.40%，綜合評分分別提高了2.38%、2.80%、2.80%、2.57%、3.45%。

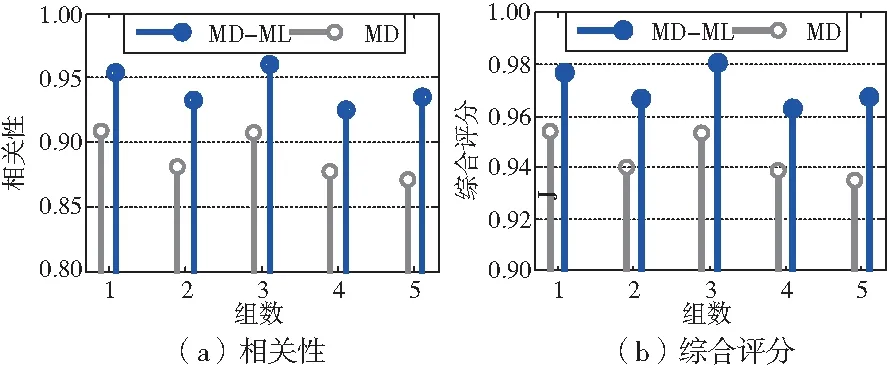
圖6 度量學習評分對比

為了對比本文方法的有效性，采取未度量學習的馬氏距離函數MD-SVR、歐氏距離函數ED-SVR以及GMM-SVR、MDML-Logistic方法進行分析。

根據太陽輪點蝕損傷程度預先設定健康指標，正常狀態ds0時HI=1，ds1-ds4時，HI分別為0.8、0.6、0.4、0.2。分析與圖7中度量學習前后健康評估結果可以發現，采用本文方法得到的HI更貼合實際結果，隨故障加深而減小，且不同健康狀態區分明顯，符合預期結果。其他方法在正常狀態ds0與ds1時的評估結果非常接近，不足以區分健康狀態。ED-SVR與GMM-SVR在ds1的HI大于正常狀態ds0的HI，不符合實際結果。

圖7 健康評估結果比較

為了準確、全面地比較健康評估結果，對HI隨故障程度變化曲線進行評價，如表3所示。MDML-SVR方法的相關性與綜合評分最高，分別為0.991 2與0.995 6，其次是MD-SVR、MDML-Logistic，ED-SVR、GMM-SVR最低。

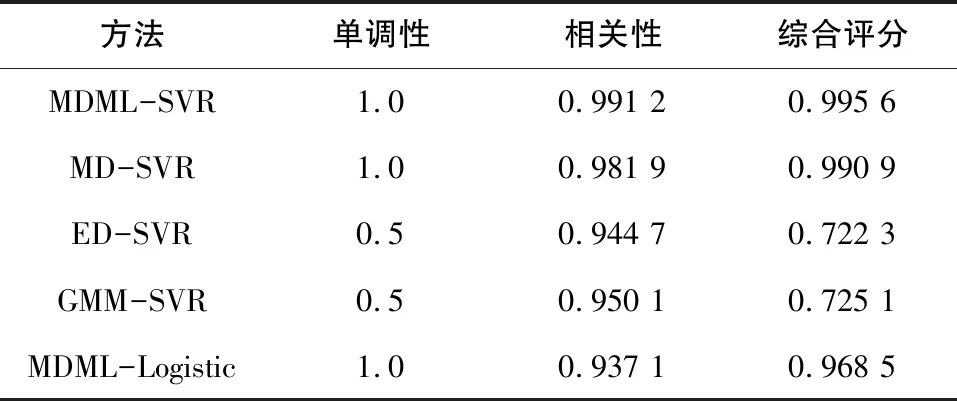
表3 健康指標評分

采用方均根誤差(RMSE)、平均絕對誤差(MAE)、平均百分比誤差(MAPE)對健康評估結果進行評價，結果見表4。MDML-SVR的RMSE、MAE、MAPE分別為0.047 3、0.027 8、0.036 4，均優于其他方法。綜合以上分析，本文所提健康評估方法效果優異，可以有效提高行星齒輪箱健康評估準確率。

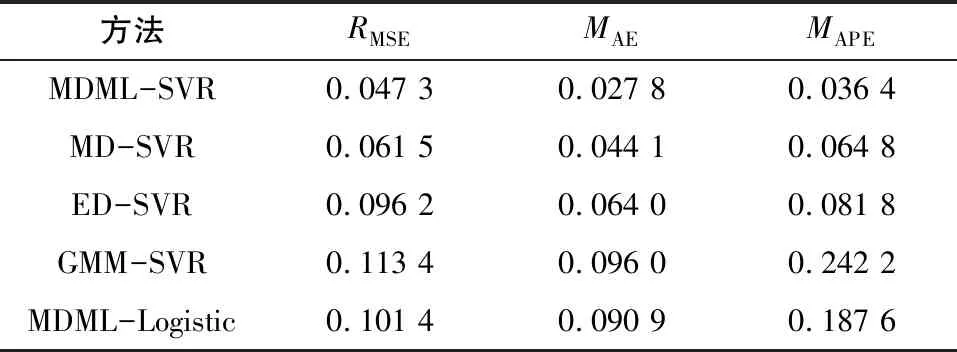
表4 健康評估誤差比較

5 結語

提出一種基于圖譜特征與度量學習的行星齒輪箱健康評估方法，通過實驗結果分析，得出結論：

1) 圖譜特征作為故障特征參數，在表征故障嚴重程度方面優于常用的時域、頻域特征。

2) 將單調性與相關性作為度量學習準則，可以減小不同故障嚴重程度下馬氏距離的波動，提高健康評估指標的單調性、準確性。

3) 基于MDML-SVR的行星齒輪箱健康評估方法評估結果更準確。